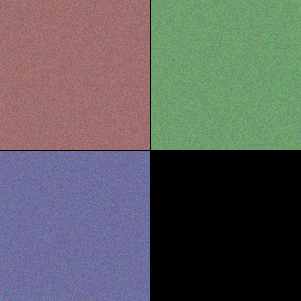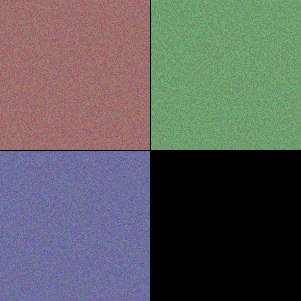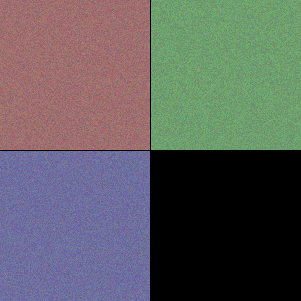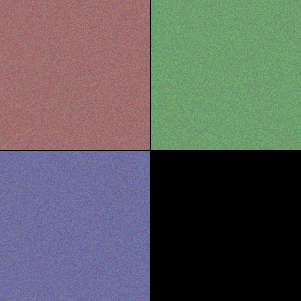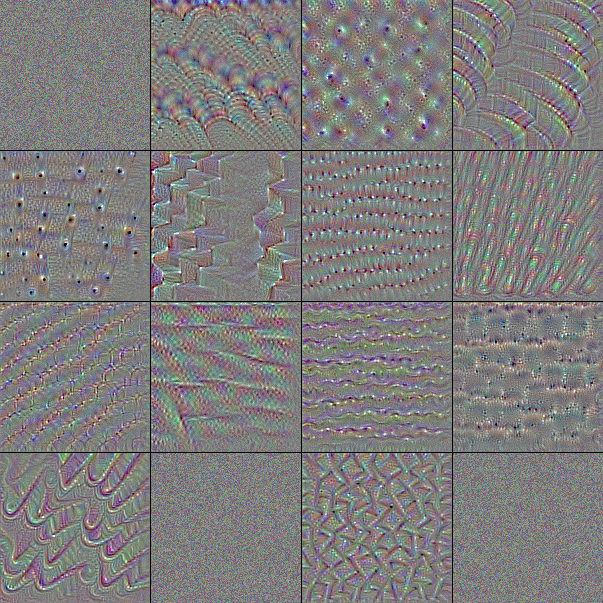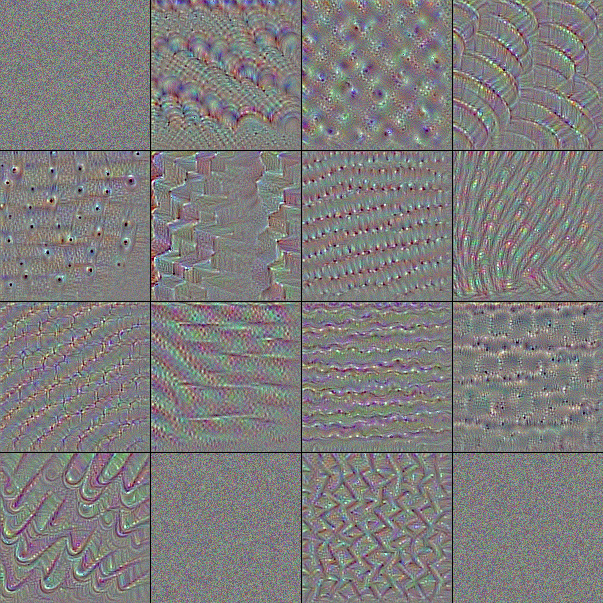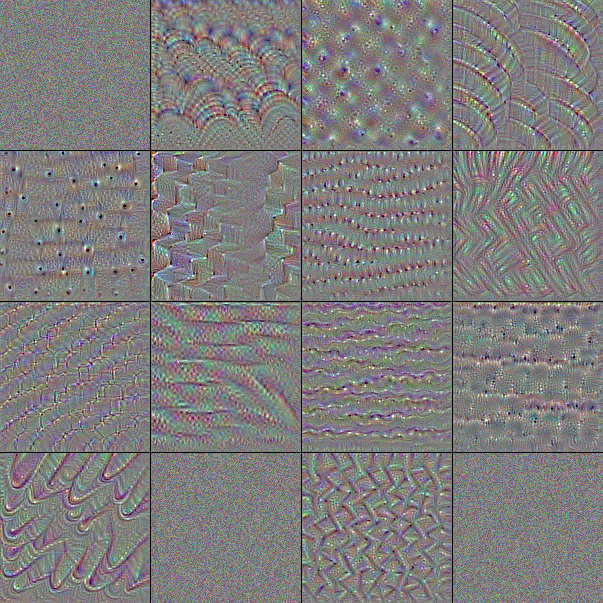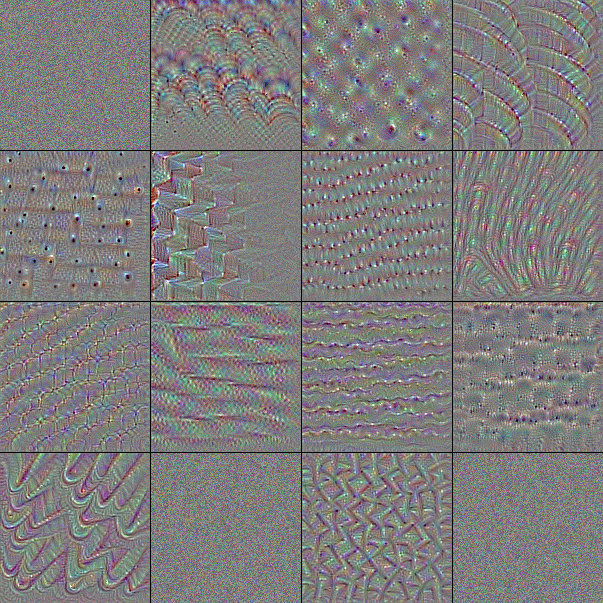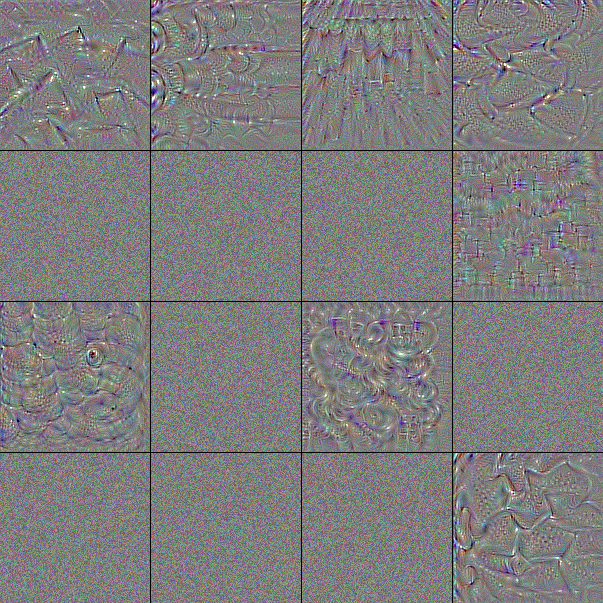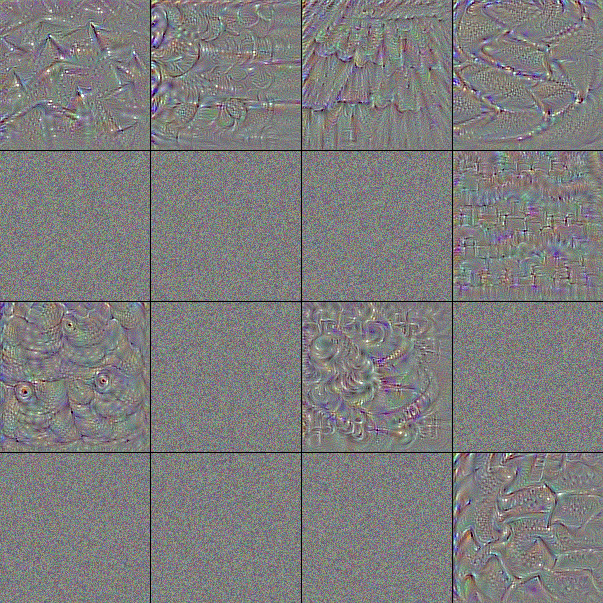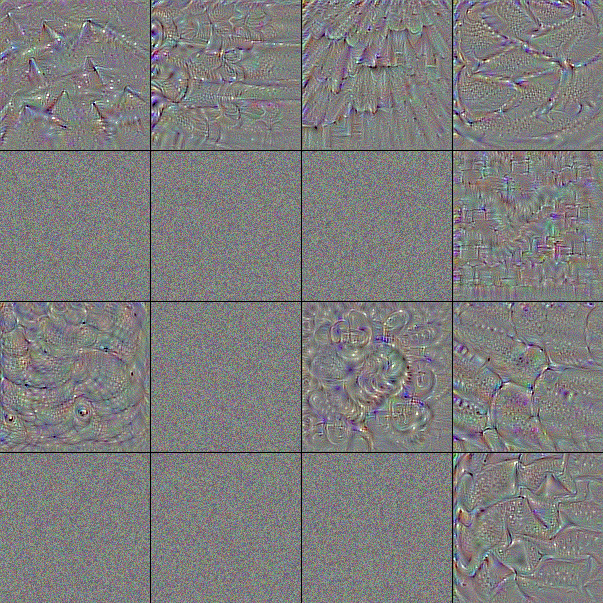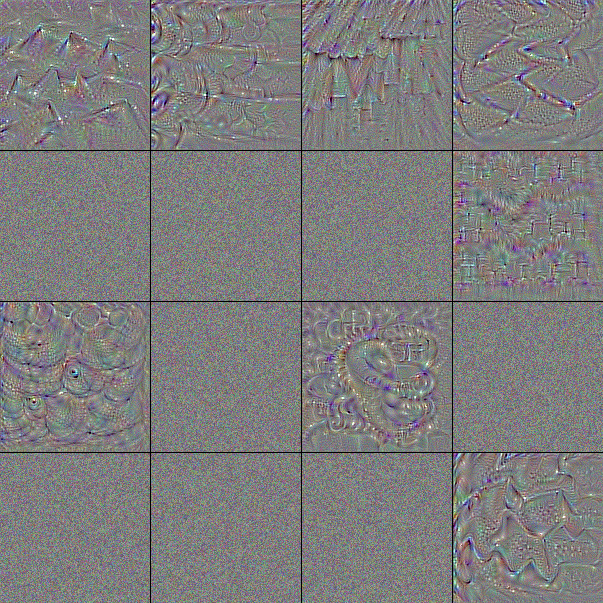畳み込みニューラルネットワーク

2018年8月13日 #ConvNet

概要

畳み込みニューラルネットワーク (convnet, CNN; convolutional neural network) はフィードフォーワード型の深層ニューラルネットワーク (DNN; deep neural network) の一種。主に画像や映像に対する物体認識分野において良好な性能を示している。

教師データで訓練された convnet は畳み込み層とプーリング層によって特徴量抽出器として機能する。一般に、この特徴量を入力とする全結合層 (分類器) を後続に配置して convnet 全体を分類タスクや回帰タスクに利用することが多い。

ここでの分類器は SVM など DNN 以外のアルゴリズムとの置き換えを検討することができる。また抽出された特徴量を分類以外のタスクに使用することも可能である (このページでは分類層に関する説明は特に行わない)。

すべての特徴を密に関連付ける全結合のネットワークと異なり、畳み込みによるネットワークは雑多な特徴から学習タスクに本質的ではない特徴の重要性を落とし、本質的な特徴量のみを強調するように訓練される。

畳み込みニューラルネットワークの構造

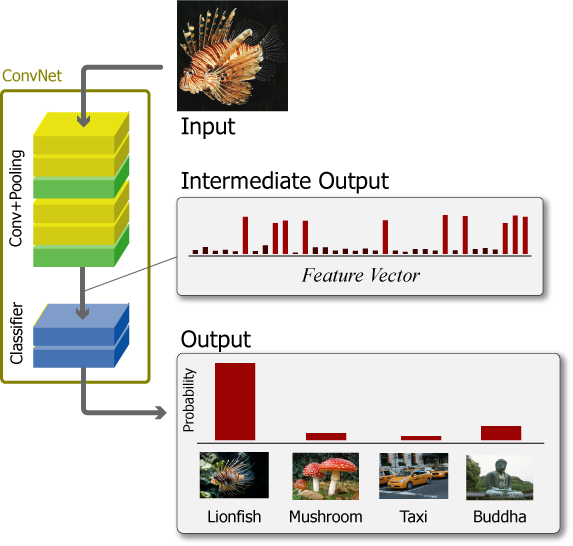
一般的な convnet は入力層、出力層といくつかの隠し層で構成されている。隠し層には正規化層や全結合層など、目的の異なるいくつもの層が繰り返し重なって構成されるが、convnet の機能を特徴づけているのは畳み込み層 (convolution layer) とプーリング層 (pooling layer) である。

convnet は 1 つのサンプル (画像) を縦×横の空間次元軸 + 深さ軸を持った階数 3 のテンソルとして扱う。例えば最初の入力となるテンソルは RGB 各チャンネルが深さに対応したカラー画像である。これは「赤、緑、青の『色』を特徴として反応するフィルタを通った結果」とみなすことができる。

convnet に入力されたテンソルが畳み込み層とプーリング層を通過すると、縦横の次元が縮小され、代わりに特定の特徴に対して反応するした活性化パターンが深さとして増加する。この操作を繰り返して最終的に縦横が 1～10 程度で数千程度の深さを持つテンソルに変換される。

特徴量の可視化

2次元 convnet の出力として得られるテンソルは、入力画像を特徴付ける部分が活性化された大量で微細な 2 次元行列である。これらは入力画像が持つ特徴によって点灯/消灯するシグナルのように機能する。

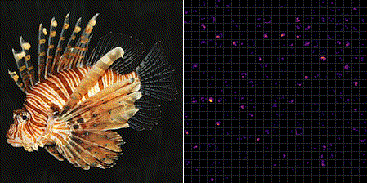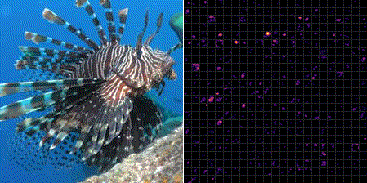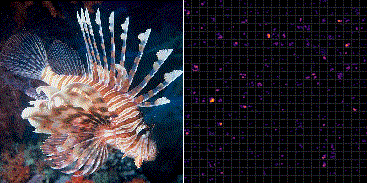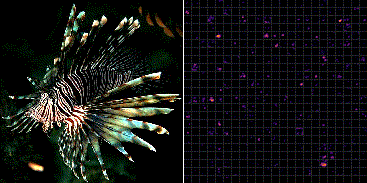
Fig.3 ImageNet 学習済み VGG-16 におけるミノカサゴとカワセミの特徴量出力。

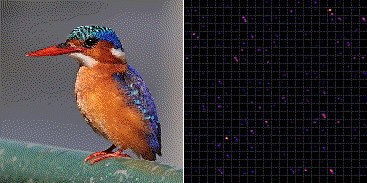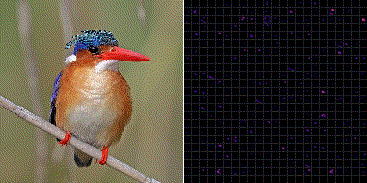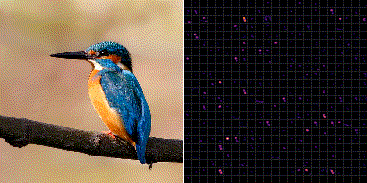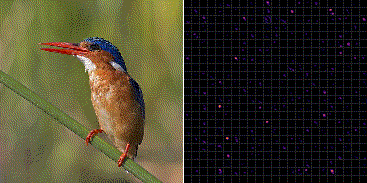
Fig.3 は ImageNet で学習した VGG-16 の最後のプーリング層 (block5_pool) から出力される 7×7 の強度をヒートマップ化し縦横に 512 枚並べている。

ミノカサゴの入力画像に対していくつかのフィルタが共通して反応していることが分かる。一方でそれらの輝点はカワセミ画像の入力に対して反応していない。これより、どの輝点が反応し、また反応していないかを統計的に分類することで、ミノカサゴとカワセミの画像識別を行うことができる。

微細化された特徴強度のテンソル (つまり Fig.3 右側のヒートマップ) は Flatten や MaxPooling の操作を行うことで特徴ベクトル化することができる。例えば VGG-16 は 7×7×512 出力をピクセル単位に平坦化し 25,088 個の特徴量に変換している。

畳み込み層

畳み込み層は入力信号 (画像) を変換する複数のフィルタによって構成されている。学習によって調整されるフィルタは局所的な特徴パターンに反応する小さな行列で表される。このため畳み込み層は対象の画像が大きくなっても重みパラメータは増加しない。

畳み込み演算

畳み込みとは行列をカーネルと呼ばれる別の行列に重ね足し合わせる処理である。画像変換では、カーネルの値を変化させるだけで「輪郭強調」「エンボス」といった簡単だが多彩な効果をもたらすことができる。この特性を利用して、畳み込み層は最終的に出力される特徴量が最も明確な差異となるようにすべてのカーネルの行列値を調整する。

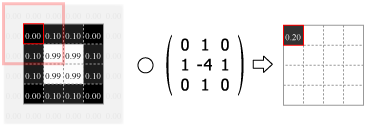
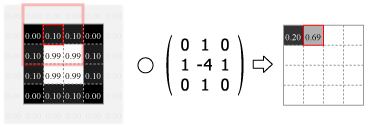
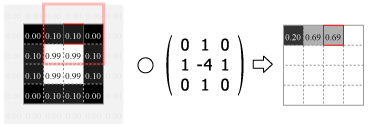
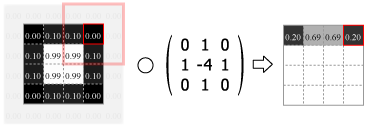
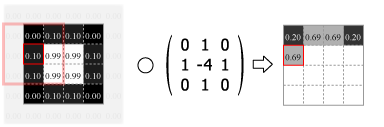
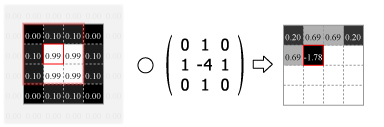
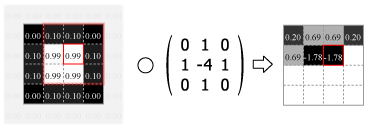
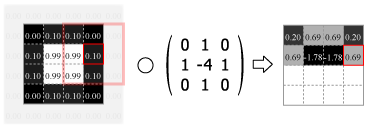
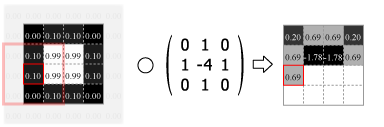
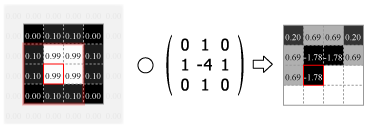
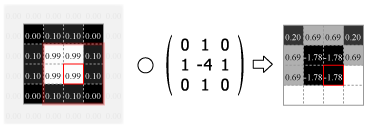
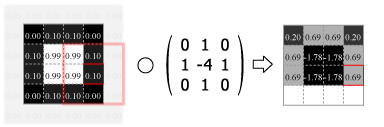
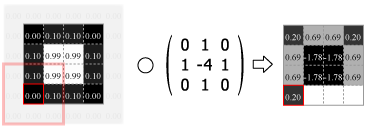
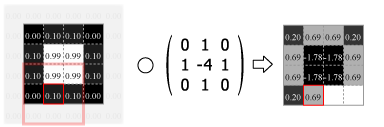
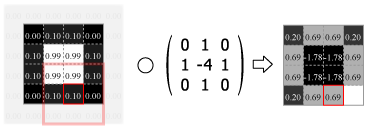
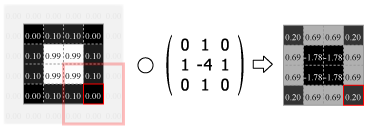
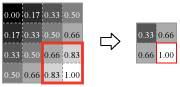
畳み込みの処理はカーネルの中心を画像のピクセルに合わせ、重なり合ったそれぞれの要素の積を合計した値をその位置の出力値とする。この操作をスライドさせながら画像のすべてのピクセルに対して適用する。

Fig.4 3×3 カーネルをストライド 1、パディング 0.0 で畳み込みに適用した場合。

Fig.4 は画像の外側をすべて 0.0 でパディングしているが、他にも画像中の最も近いピクセルに合わせたり、鏡面反射のように折り返されていると想定するなどのパディング方法がある。パディングを使用すると元の画像と同じサイズの出力を得ることができるが、カーネルが画像の外にはみ出すことを許さない (padding="valid") 場合の出力は縦横にカーネルサイズの半分だけ小さくなる。またストライド (スライド量) が 1 より大きい場合はその逆数だけ出力は縮小する。

Numpy を使用した 2 次元の畳み込み演算は scipy の convolve2d() で行うことができる。Fig.4 のカーネルをグレイスケール画像に適用すると Fig.5 のようになる。

import numpy as np
from PIL import Image
from scipy import signal

kernel = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])
img = Image.open("circle1.png").convert("L")
img = np.asarray(img)
img = img / 255.

dst = signal.convolve2d(img, kernel)
Image.fromarray((dst * 255.).astype(np.uint8)).save("circle2.png")

Fig.5 輪郭抽出効果のあるカーネルを適用して畳み込みを行ったグレイスケール画像。

畳み込み演算は 2 次元の局所パターンを学習することから、強調すべき特徴のパターンが画像上のどの位置に現れても正しく認識する移動不変性を持つ。ただし、コンピュータビジョンで必要な回転や拡大縮小の不変性はほぼ効果がないため、学習時にデータ拡張を用いるなどの工夫は有効である。

このページでは単純な例示のために入出力ともに 2 次元の行列 (2階のテンソル) として扱っているが、実際の畳み込み層の入出力は深さを持っている。例えば RGB 3 チャンネルの深さを持つ画像を 3✕3 のカーネルで畳み込む場合、1 つのフィルターは 3✕3✕3 (入力チャンネル数✕カーネル幅✕カーネル高) の形をしている。さらに、64 個の特徴強度を出力する畳み込み層であれば 64 個のフィルタで構成されていて、その層は 3✕3✕3✕64 個の重みパラメータが存在することになる。

フィルタの可視化

Block1 Conv1 — Fig.6 VGG-16 + ImageNet フィルタに最も反応する画像。

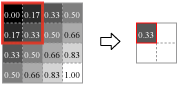
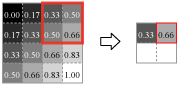
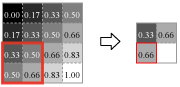
フィルタは小さな行列による演算処理であるため映像化することはできないが、そのフィルタを通したときに最も強く反応する画像からそのフィルタが認識する特徴を伺うことはできる。Fig.6 は ImageNet で学習済みの VGG-16 が含むフィルタを最大 16 個を取り出し、それぞれに勾配降下法で作成した「出力が最も活性化する画像」である。

最初の入力層 input は赤、緑、青の色に反応する 3 つのフィルタである。これは入力テンソルが RGB の 3 つのカラーチャンネルを持っていることから明かであろう。

表層の block1 はべた塗りの色と砂のような単純な模様に反応するフィルタから成る。中間層の block2, block3 では模様がより高度になり形をとらえられるようになっている。block4, block5 では何かしらの物体的特徴をとらえるように変化している。

ノイズのみのフィルタや、大半がノイズのままになっているフィルタは勾配降下のイテレーションでうまく収束しなかった画像である。実際には何らかの有効なフィルタが機能している。

プーリング層

プーリング層は畳み込み層によって強調された特徴強度を維持しつつ縦横の空間次元を圧縮するために使用されている。これにより 1)データが縮小されるため後続の計算量が軽減され 2)パラメータが減少するため過学習の可能性を軽減でき 3)領域内の微細な位置の違いが無視されることから出力に頑健な移動不変性が持たせられる。

ただし、例えばボードゲームや TV ゲームにおける戦況把握のように、映像上での物体の「位置」を含めて学習するタスクではプーリング層を使用しないこともある。

Fig.7 サイズ2×2、ストライド(2,2)の Max Pooling による縮小。

Fig.7 はウィンドウをスライドさせながらウィンドウ内の最大値を出力する、convnet で最も一般的に使用されている Max Pooling 法の順方向伝搬の動きを示している。

Max Pooling はカーネルサイズ \(K\)、ウィンドウのスライド量であるストライド \(S\) をパラメータとして持ち、入力テンソル \(W_1 \times H_1 \times D \times N\) を出力テンソル \(W_2 \times H_2 \times D \times N\) へ変換する。ここで: \[ \begin{eqnarray*} W_2 & = & (W_1 - K) / S + 1 \\ H_2 & = & (H_1 - K) / S + 1 \end{eqnarray*} \]

プーリング層に学習可能なパラメータが存在しないことをは明かであろう。従ってプーリング層の逆方向伝搬の動作も単純である。Max Pooling の順方向伝搬がウィンドウ内で最大値を持つピクセルに 1 を、それ以外に 0 を乗算することと同じであると考えると、逆方向伝搬は順方向伝搬で最大値を持っていたピクセルに入力勾配 \({\rm dout}\) を、それ以外に 0 伝搬する。

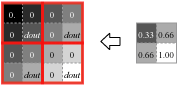
この動作からプーリング層の逆方向伝搬は入力勾配を単純にルーティングしているだけとも考えられる。

デモンストレーション

以下は ImageNet で学習済みの VGG-16 の各レイヤーに対して 1)最も反応の強い画像と 2)カワセミを適用した特徴強度を元の画像とい重ね合わせて示している。レイヤーを選択しマウスカーソルを当てるとその位置のフィルタがどの部分を特徴としてとらえているかが表示される。オーバーレイに「通常」を選択するとヒートマップのみが表示される。