論文翻訳: From Word Embeddings To Document Distances

Abstract

我々はテキスト文書間の新しい距離関数である Word Mover's Distance (WMD) を提示する。我々の研究は文中の局所的な共起から単語の意味的に重要な表現を学習する単語埋め込み (word embedding) の最近の研究結果に基づいている。WMD 距離は、2 つのテキスト文書間の非類似度を、一方の文書に埋め込まれた単語が別の文書に埋め込まれた単語に到達するまでに「移動」する必要がある最小の距離量として算出する。我々はこの距離メトリクスが、いくつかの非常に効率的なソルバーが開発されているよく研究された移動問題である Earth Mover's Distance の具体例となることを示す。我々のメトリクスはハイパーパラメータを持たず簡単に実装することができる。さらに WMD メトリクスが 7 つの最先端のベースラインと比較して 8 つの現実世界の文書分類データセットで前例のない低 k-nearest となることを実証する。

Table of Contents

1. Abstract
2. 1 Introduction
3. 2 Related Work [under construction]
4. 3 Word2Vec Embedding
5. 4 Word Mover's Distance
   1. 4.1 Fast Distance Computation
6. 5 Results
   1. 5.1 Dataset Description and Setup
   2. 5.2 Document Classification
   3. 5.3 Word Embeddings
   4. 5.4 Lower Bounds and Pruning
7. 6 Discussion and Conclusion
8. Acknowledgments
9. References
10. 翻訳抄

1 Introduction

2 つの文書間の距離を正確に表すことは、文書検索 ((Salton & Buckley, 1988)、ニュースのカテゴライズやクラスタリング (Ontrup & Ritter, 2001; Greene & Cunningham, 2006)、歌詞の識別 (Brochu & Freitas, 2002)、多言語文書検索 (Quadrianto et al., 2009) などの広範囲に及ぶ応用がある。

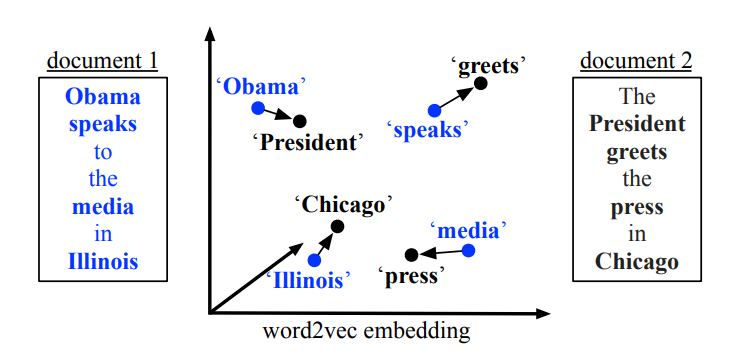
文書を表現する最も一般的な 2 つの方法は単語の Bag of Words (BOW) と BOW による TF-IDF である。しかしこれらの特徴はほとんどが直行するため文書の距離には適していないことが多い (Schölkopf et al., 2002; Greene & Cunningham, 2006)。これらの表現の最も重大な欠点は個々の単語間の距離を考慮しないことである。例として "Obama speaks to the media in Illinois" と "The President greets the press in Chicago" という 2 つの異なる文書を取り上げる。これらの文書に共通する単語は存在しないがほぼ同じ情報を伝えている。これらは BOW モデルでは表現できない事実である。この場合、単語ペアの近さ (Obama, President), (speaks, greets), (media, press), (Illinois, Chicago) は BOW に基づいた距離では考慮されていない。

文書の潜在的な低次元表現を学習することによってこのっ問題を回避しようとする多くの方法が存在する。Latent Semantic Indexing (LSI) (Deerwester et al., 1990) は BOW 特徴空間を固有分解 (eugendecomposition) し、Latent Dirichlet Allocation（LDA) (Blei et al., 2003) は確率的に類似単語をトピックへグループ化した。同時に BOW / TF-IDF 変種の競合が多く存在している (Salton & Buckley, 1988; Robertson & Walker, 1994)。これらの手法は BOW よりも一貫した文書表現を生成するが、距離に基づく研究 (例えば nearest-neighbor classfier) において BOW の実験的性能をを改善しないことが多い (Petterson et al., 2010; Mikolov et al., 2013c)。

Figure 1. Word Mover's Distance の図。両文書の全ての非ストップワード (bold) は Word2Vec 空間に埋め込まれる。2 文書間の距離は文書 1 の全ての単語が文書 2 と完全に一致するまでに移動する距離の累積の最小値である (最良の結果は色付きで示している)。

この論文ではテキスト文書間の距離に関する新しいメトリクスを導入する。我々のアプローチは、名高い Word2Vec モデルが前例のない品質の単語埋め込みを生成し、非常に大きなデータセットに対して自然にスケールする Mikolov et al. (2013b) による最新の結果を活用している (例えば我々は約 1,000 億単語で訓練された自由に利用できるモデルを使用する)。この著者らは vec(Berlin) - vec(Germany) + vec(France) が vec(Paris) の近くを示すなど、単語ベクトルに対するベクトル演算で意味関係がしばしば保存されることを示している。これは、埋め込まれた単語ベクトルの間と距離が意味的に重要であることを示唆している。我々の Word Mover's Distance (WMD) と呼ばれるメトリクスはこの Word2Vec 埋め込みの特性を使用している。テキスト文書は埋め込まれた単語の加重点群として表現される。2つの適すt文書 A と B の間の距離は、文書 A に含まれる単語が文書 B の点群と正確に一致するために移動する必要がある最小累積距離である。Figure 1 は我々の新しいメトリクスの概略図を示している。

WMD の基礎となる最適化問題は、よく研究された Earth Mover's Distance (Rubner et al., 1998) の移動問題の特殊なケースに帰着し、高速な専用ソルバーに関する既存の文献を活用することができる (Pele & Werman, 2009)。またいくつかの下限を比較しこれらを近似として使用したり、クエリーに対して k 近傍にない文書を除外することができることを示す。

WMD 距離にはいくつかの興味深い特徴がある: 1. ハイパーパラメータがなく理解が容易 2. ２つの文書館の距離を個々の単語間の疎な距離として分解し説明できるため非常に解釈が容易 3. Word2Vec 空間にエンコードされた知識を組み込み高い検索精度をもたらす ── これは並行する 7 つの文書距離最先端研究に対して、現実世界における 8 つの分類実験のうち 6 つにおいて優れている。

2 Related Work

3 Word2Vec Embedding

4 Word Mover's Distance

\(n\) 単語の有限サイズのボキャブラリに対する Word2Vec 埋め込み行列 \(\vector{X} \in \mathbb{R}^{d \times n}\) が与えられていると仮定する。\(i\) 番目のカラム \(x_i \in \mathcal{R}^d\) は \(d\) 次元空間における \(i\) 番目の単語の埋め込みを表している。テキスト文書は正規化された Bag-of-Words (nBOW) ベクトル \(\vector{d} \in \mathcal{R}^n\) として表されるとする。正確には単語 \(i\) がドキュメント内に \(c_i\) 回出現した場合 \(d_i = \frac{c_i}{\sum_{j=1}^n c_j}\) である。単語の大部分が任意の文書には現れず、nBOW ベクトル \(\vector{d}\) は本来的に非常に疎である (我々はカテゴリに依存しないストップワードを削除する)。

nBOW 表現: ベクトル \(\vector{d}\) は単語分布の \(n-1\) 次元単体 (simplex) 上の点と考えることができる。異なるユニーク単語を持つ 2 つの文書はこの単体上の異なる領域に配置される。しかしながら、これらの文書はまだ意味的に近いかもしれない。似ているが単語が異なっている例は前述の "Obama speaks to the media in Illinois" と "The President greets the press in Chicago" を参照。これらはストップワード削除後、2 つの対応する nBOW ベクトル \(\vector{d}\) と \(\vector{d}'\) が共通の非ゼロ次元を持たないため、真の距離は小さいが単体距離は最大に近い。

単語移動コスト: 我々の目的は個々の単語ペア (例えば President と Obama) 間の意味的類似度を文書の距離メトリクスに組み込むことである。そのような単語の非類似度の尺度の一つは Word2Vec 埋め込み空間でのユークリッド距離によって提供される。より正確には、単語 \(i\) と \(j\) 間の距離は \(c(i,j) = \|\vector{x}_i - \vector{x}_j\|_2\) となる。単語の距離と文書の距離が混乱することを避けるため、我々はある単語から別の単語への「移動」に関するコストに \(c(i,j)\) を使用する。

ドキュメント距離: 2つの単語間の「移動コスト」は 2 つの文書間の距離を構築するための自然な構成要素である。\(\vector{d}\) と \(\vector{d}'\) を \(n-1\) 単体における 1 つのドキュメントの nBOW 表現とする。まず、\(\vector{d}\) 内の各単語 \(i\) を \(\vector{d}'\) 内全てまたは一部の任意の単語 \(j\) に変換する。\(\vector{T} \in \mathcal{R}^{n \times n}\) を (疎な) フロー行列とする。ここで \(\vector{T}_{ij} \geq 0\) は \(\vector{d}\) 内の単語 \(i\) が \(\vector{d}'\) 内の単語 \(j\) にどれだけ移動するかを示す。\(\vector{d}\) を完全に \(\vector{d}'\) に変換するため、単語 \(i\) からの出力フロー全体が \(d_i\) と等しくする。すなはち \(\sum_j \vector{T}_{ij} = d_i\)。さらに、単語 \(j\) に到達するフローの量は \(d'_j\) と一致しなければならない。すはなち \(\sum_i \vector{T}_{ij} = d'_j\) である。最後に、我々は \(\vector{d}\) から \(\vector{d}'\) へすべての単語を移動するために必要な最小 (重み付け) 累積コストを 2 つの文書間の距離として定義することができる。つまり \(\sum_{i,j} \vector{T}_{ij} c(i,j)\) である。

移動問題: 数式的に、制約下で \(\vector{d}\) から \(\vector{d}'\) へ移動させるための最小累積コストは以下の線形計画によって与えられる, \[ \min_{\vector{T} \geq 0} \sum_{i,j=1}^n \vector{T}_{ij} c(i,j) \] 従って \[ \begin{equation} \sum_{j=1}^n \vector{T}_{ij} = d_i \ \ \ \ \forall i \in \{1, \ldots, n\} \\ \sum_{i=1}^n \vector{T}_{ij} = d'_j \ \ \ \ \forall j \in \{1, \ldots, n\} \end{equation} \] 上記の最適化は、専用のソルバーが開発されている (Ling & Okada, 2007; Pele & Werman, 2009) よく研究された移動問題である Earth Mover's Distance メトリクス (EMD) (Monge, 1781; Rubner et al., 1998; Nemhauser & Wolsey, 1988) の特殊なケースである。このつながりを強調するために研究結果のメトリクスを Word Mover's Distance とする。コスト \(c(i,j)\) はメトリックであるため WMD もメトリックであることが容易に分かる (Rubner et al., 1998)。

Figure 2. (上部:) クエリー \(D_0\) と 2 つの文書 \(D_1\), \(D_2\) 間の WMD メトリクス構成 (BOW 距離と等価)。矢印は 2 単語間のフローを表し、それらの距離でラベル付けされている。(下部:) 異なる数の単語を持つ 2 つの文 \(D_3\) と \(D_0\) 間のフロー。この不一致により WMD は単語を複数の類似した単語に移動させる。

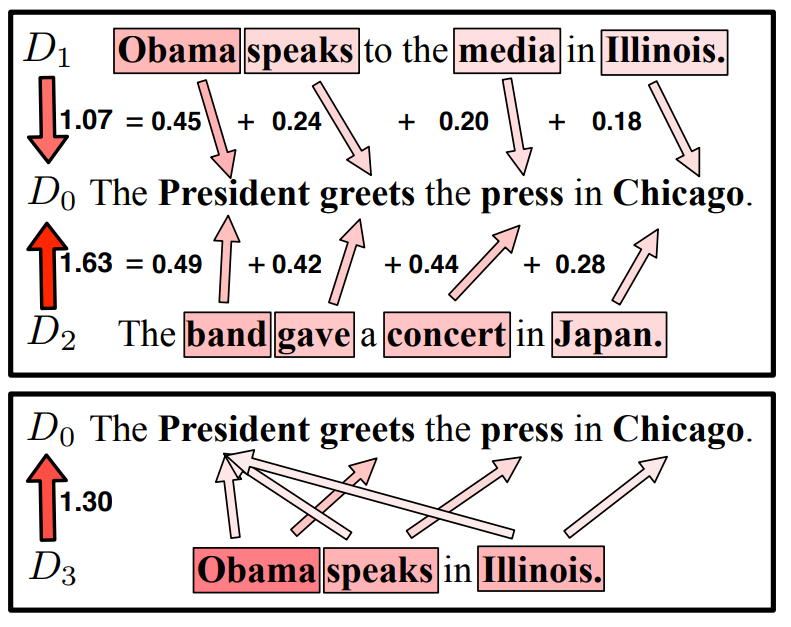
可視化: Figure 2 はクエリー文書 \(D_0\) と比較しようとしている 2 つの文書 \(D_1\) と \(D_2\) の WMD メトリクスを示している。まず最初にストップワードが削除され \(D_0\) には President, greets, press, Chicago が \(d_i=0.25\) で残る。文 \(D_1\) および \(D_2\) のそれぞれの単語 \(i\) から \(D_0\) の単語 \(j\) への矢印は距離 \(\vector{T}_{ij} c(i,j)\) によってラベル付けされている。WMD は我々の直感に応じており、意味的に似ている単語を「移動」することに注意。Illinois を Chicago に移動することは Japan を Chicago に移動するよりも低コストである。これは Word2Vec 埋め込みによって vec(Illinois) が vec(Japan) より vec(Chicago) に近い場所に配置されるためである。その結果 \(D_0\) から \(D_1\) への距離は 1.07 は \(D_2\) への距離 1.63 よりかなり小さい。ただし重要なことだが、\(D_1\) と \(D_2\) は \(D_0\) と共通の単語を有していないため、\(D_0\) からの Bag of Words / TF-IDF 距離は同じである。追加の \(D_3\) の例では単語の数が一致しない場合のフローを強調している。\(D_3\) 重み \(d_j = 0.33\) を持ち、余分なフローは他の似た単語に送られる。これは距離を増やすことになる。より長い文書にはいくつかの類似した単語が含まれている可能性があるため、文書の長さが短いために効果が人為的に拡大される可能性がある。

4.1 Fast Distance Computation

5 Results

5.1 Dataset Description and Setup

5.2 Document Classification

5.3 Word Embeddings

5.4 Lower Bounds and Pruning

6 Discussion and Conclusion

Acknowledgments

KQW and MJK are supported by NSF grants IIA-1355406, IIS-1149882, EFRI-1137211. We thank the anonymous reviewers for insightful feedback.

References

• Andoni, A. and Indyk, P. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. IFOCS, pp. 459–468. IEEE, 2006.Aslam, J. A. and Frost, M. An information-theoretic measure for document similarity. In SIGIR, volume 3, pp.449–450. Citeseer, 2003.Blei, D. M., Ng, A. Y., and Jordan, M. I. Latent dirichlet allocation. Journal of Machine Learning Research, 3: 993–1022, 2003.
• Blitzer, J., McDonald, R., and Pereira, F. Domain adaptation with structural correspondence learning. In EMNLP,pp. 120–128. ACL, 2006.
• Brochu, E. and Freitas, N. D. Name that song! In NIPS, pp. 1505–1512, 2002.
• Cardoso-Cachopo, A. Improving Methods for Single-label Text Categorization. PdD Thesis, Instituto Superior Tecnico, Universidade Tecnica de Lisboa, 2007.
• Chen, M., Xu, Z., Weinberger, K. Q., and Sha, F. Marginalized denoising autoencoders for domain adaptation. In ICML, 2012.
• Collobert, R. and Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In ICML, pp. 160–167. ACM, 2008.
• Cover, T. and Hart, P. Nearest neighbor pattern classification. Information Theory, IEEE Transactions on, 13(1):21–27, 1967.
• Croft, W. B. and Lafferty, J. Language modeling for information retrieval, volume 13. Springer, 2003.
• Cuturi, Marco. Sinkhorn distances: Lightspeed computation of optimal transport. In Advances in Neural Information Processing Systems, pp. 2292–2300, 2013.
• Deerwester, S. C., Dumais, S. T., Landauer, T. K., Furnas, G. W., and Harshman, R. A. Indexing by latent semantic analysis. Journal of the American Society of Information Science, 41(6):391–407, 1990.
• Garcia, Vincent, Debreuve, Eric, and Barlaud, Michel. Fast k nearest neighbor search using gpu. In CVPR Workshop, pp. 1–6. IEEE, 2008.
• Gardner, J., Kusner, M. J., Xu, E., Weinberger, K. Q., and Cunningham, J. Bayesian optimization with inequality constraints. In ICML, pp. 937–945, 2014.
• Glorot, X., Bordes, A., and Bengio, Y. Domain adaptation for large-scale sentiment classification: A deep learning approach. In ICML, pp. 513–520, 2011.
• Grauman, K. and Darrell, T. Fast contour matching using approximate earth mover’s distance. In CVPR, volume 1, pp. I–220. IEEE, 2004.
• Greene, D. and Cunningham, P. Practical solutions to the problem of diagonal dominance in kernel document clustering. In ICML, pp. 377–384. ACM, 2006.
• Hearst, M. A. Multi-paragraph segmentation of expository text. In ACL, pp. 9–16. Association for Computational Linguistics, 1994.
• Jojic, N. and Perina, A. Multidimensional counting grids: Inferring word order from disordered bags of words. In UAI. 2011.
• Le, Quoc V and Mikolov, Tomas. Distributed representations of sentences and documents. In ICML, 2014.
• Levina, E. and Bickel, P. The earth mover’s distance is the mallows distance: Some insights from statistics. In ICCV, volume 2, pp. 251–256. IEEE, 2001.
• Ling, Haibin and Okada, Kazunori. An efficient earth mover’s distance algorithm for robust histogram comparison. Pattern Analysis and Machine Intelligence, 29(5): 840–853, 2007.
• Mikolov, T., Chen, K., Corrado, G., and Dean, J. Efficient estimation of word representations in vector space. In Proceedsings of Workshop at ICLR, 2013a.
• Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. Distributed representations of words and phrases and their compositionality. In NIPS, pp. 3111–3119, 2013b. Mikolov, T., Yih, W., and Zweig, G. Linguistic regularities in continuous space word representations. In NAACL, pp. 746–751. Citeseer, 2013c.
• Mnih, A. and Hinton, G. E. A scalable hierarchical distributed language model. In NIPS, pp. 1081–1088, 2009.
• Monge, G. Memoire sur la th ´ eorie des d ´ eblais et des rem- ´blais. De l’Imprimerie Royale, 1781.
• Nemhauser, G. L. and Wolsey, L. A. Integer and combinatorial optimization, volume 18. Wiley New York, 1988.
• Ontrup, J. and Ritter, H. Hyperbolic self-organizing maps for semantic navigation. In NIPS, volume 14, pp. 2001, 2001.
• Pele, O. and Werman, M. Fast and robust earth mover's distances. In ICCV, pp. 460–467. IEEE, 2009.
• Perina, A., Jojic, N., Bicego, M., and Truski, A. Documents as multiple overlapping windows into grids of counts. In NIPS, pp. 10–18. 2013.
• Petterson, J., Buntine, W., Narayanamurthy, S. M., Caetano, T. S., and Smola, A. J. Word features for latent dirichlet allocation. In NIPS, pp. 1921–1929, 2010.
• Quadrianto, N., Song, L., and Smola, A. J. Kernelized sorting. In NIPS, pp. 1289–1296, 2009.
• Ren, Z., Yuan, J., and Zhang, Z. Robust hand gesture recognition based on finger-earth mover’s distance with a commodity depth camera. In Proceedings of ACM international conference on multimedia, pp. 1093–1096. ACM, 2011.
• Robertson, S. E. and Walker, S. Some simple effective approximations to the 2-poisson model for probabilistic weighted retrieval. In Proceedings ACM SIGIR conference on Research and development in information retrieval, pp. 232–241. Springer-Verlag New York, Inc., 1994.
• Robertson, S. E., Walker, S., Jones, S., Hancock-Beaulieu, M. M., Gatford, M., et al. Okapi at trec-3. NIST SPECIAL PUBLICATION SP, pp. 109–109, 1995.
• Rubner, Y., Tomasi, C., and Guibas, L. J. A metric for distributions with applications to image databases. In ICCV, pp. 59–66. IEEE, 1998.
• Salton, G. and Buckley, C. The smart retrieval systemexperiments in automatic document processing. 1971.
• Salton, G. and Buckley, C. Term-weighting approaches in automatic text retrieval. Information processing & management, 24(5):513–523, 1988.
• Sanders, N. J. Sanders-twitter sentiment corpus, 2011.
• Scholkopf, B., Weston, J., Eskin, E., Leslie, C., and No- ¨ble, W. S. A kernel approach for learning from almost orthogonal patterns. In ECML, pp. 511–528. Springer, 2002.
• Shirdhonkar, S. and Jacobs, D. W. Approximate earth movers distance in linear time. In CVPR, pp. 1–8. IEEE, 2008.
• Snoek, J., Larochelle, H., and Adams, R. P. Practical bayesian optimization of machine learning algorithms. In NIPS, pp. 2951–2959, 2012.
• Steyvers, M. and Griffiths, T. Probabilistic topic models. Handbook of latent semantic analysis, 427(7):424–440,2007.
• Turian, J., Ratinov, L., and Bengio, Y. Word representations: a simple and general method for semi-supervised learning. In ACL, pp. 384–394. Association for Computational Linguistics, 2010.
• Wan, X. A novel document similarity measure based on earth movers distance. Information Sciences, 177(18): 3718–3730, 2007.
• Yianilos, Peter N. Data structures and algorithms for nearest neighbor search in general metric spaces. In Proceedings of ACM-SIAM Symposium on Discrete Algorithms, pp. 311–321. Society for Industrial and Applied Mathematics, 1993.

翻訳抄

Word2Vec 分散表現を使用して文の距離を算出するためのアルゴリズム Word Mover's Distance (2015) に関する論文。

• 原文: From Word Embeddings To Document Distances
• Word Mover's Distance: word2vecの文書間距離への応用