\( \def\vector#1{\boldsymbol{#1}} \)

群論

2019年10月10日 #群論

群

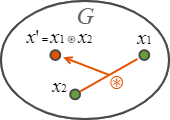
集合とその演算や作用によって定まる構造を代数的構造という。ある集合 \(G\) 上の要素 \(a,b \in G\) に対して \(c = a \ast b \in G\) となるような何らかの演算 \(\ast\) が定義されているとき、集合 \(G\) は代数系であり \((G,\ast)\) や単に \(\mathbb{G}\) と表される。演算 \(\ast\) が以下を満たしている場合 \(\mathbb{G}\) は群 (group) である。

結合律: 任意の \(a,b,c \in G\) に対して \((a \ast b) \ast c = a \ast (b \ast c)\) となる。
単位元: 任意の \(a \in G\) に対して \(a \ast e = e \ast a = a\) となる \(e \in G\) が存在する。
逆元: 任意の \(a \in G\) に対して \(a \ast a' = a' \ast a = e\) となる \(a'\) が存在する。

群の性質に加えて、以下の交換律を満たしている群は可換群 (commutative group) またはアーベル群 (abelian group) である。

交換律: 任意の \(a,b \in G\) に対して \(a \ast b = b \ast a\) が成り立つ。

また結合律のみを満たす集合と演算を半群 (semigroup)、結合率と単位元を満たす集合と演算をモノイド (monoid) と呼ぶ。

群を構成する集合の要素を元 (element) と呼ぶ。\(a^m=e\) となるよう自然数 \(m\) が存在するとき元 \(a\) は有限位数であり、そのような \(m\) の最小値を元 \(a\) の位数と呼ぶ。どのような自然数 \(m\) についても \(a^m\neq e\) であるとき \(a\) は無限位数であると言う。

\(G\) が有限集合のとき、つまり位数が有限の群 \(\mathbb{G}\) を有限群 (finite group) と呼び、有限群 \(\mathbb{G}\) に属する元の個数も (有限集合の意味の) 位数 (order) と呼び \(|G|\) と表すことができる。

例えば位数 \(n\) の整数集合を \(Z_n = \{0, 1, \ldots, n-1\}\) と定義する。\(a, b \in Z_n\) に対し \(a+b\) を \((a + b) \bmod n\) とすると群 \((Z_n, +)\) は有限な可換群となる。同様に、素数 \(p\) に対して \(Z_p^* = \{1, 2, \ldots, p-1\}\) と定義する。\(a, b \in Z_p^*\) に対して \(a \times b\) を \((a \times b) \bmod p\) とすると、\((Z_p^*, \times)\) は有限な可換群となる。

巡回群

集合 \(G\) がある一つの元 \(g\) の演算 \(\ast\) によって生成される群である場合、\(\mathbb{G}\) は巡回群 (cyclic group) である。つまり \(\mathbb{G}\) のすべての元は \(g\) の整数冪として表すことができる。\[ \mathbb{G} = \{\ldots,g^{-1}\ast g^{-1},g^{-1},1,g,g \ast g,\ldots\} = \langle g \rangle = \{g^n | n \in \mathbb{Z}\} \] ここで \(\mathbb{Z}\) は整数の全体からなる集合である。このような \(g\) を生成元 (generator) あるいは原始元 (primitive) と呼ぶ。巡回群は交換律を持つため可換群である。

結合律: \((g^a \ast g^b) \ast g^c = g^a \ast (g^b \ast g^c)\)
単位元: \(e=1\)
逆元: \(g^a \ast g^{-a} = g^{-a} \ast g^a = e = 1\)
交換律: \(g^a \ast g^b = g^b \ast g^a\)

素数の位数 \(p\) を持つ有限群 \(\mathbb{G}\) について考える。\(\mathbb{G}\) 上の単位元ではない任意の元 \(g\) の位数は \(p\) の約数となることから \(1\) か \(p\) かしか取り得ないが、前提 \(g \neq e\) より必然的に \(p\) となる。これは、元 \(g\) を生成元とした巡回群 \(\{1,g,g^2,\ldots,g^{p-1}\}\) が群 \(\mathbb{G}\) 自身と一致することを意味している。従って、素数位数を持ち \(|\mathbb{G}|\neq 1\) である群は巡回群となる。

加法群と乗法群

加減法とみなせる演算を持つ群を加法群 (additive group) と呼ぶ。加法群は単位元を 0 とし、\(a\) の逆元を \(-a\) で表すことができる可換群である。\(n\) 個の元 \(a\) の加算を \(a + \ldots + a = na\) と表す。

結合律: \((a + b) + c = a + (b + c)\)
単位元: \(e=0\)
逆元: \(a + (-a) = (-a) + a = e = 0\)
交換律: \(a + b = b + a\)

同様に、乗法とみなせる演算を持つ群を乗法群 (multicative group) と呼ぶ。乗法群は単位元を 1 とし、\(a\) の逆元を \(a^{-1}\) で表すことができる可換群である。\(a\) と \(b\) の乗算を \(ab\) と表し、\(n\) 個の元 \(a\) の乗算を \(a \times \ldots \times a = a^n\) と表す。

結合律: \((a \times b) \times c = a \times (b \times c)\)
単位元: \(e=1\)
逆元: \(a \times a^{-1} = a^{-1} \times a = e = 1\)
交換律: \(a \times b = b \times a\)

巡回群 \(\mathbb{G}\) において生成元を \(g\) としたとき、

写像

集合 \(A\) 上の全ての要素を集合 \(B\) 上の特定の要素と対応づける規則を写像 (map) または関数 (function) といい \(f: A \to B\) で表す。

写像 \(f:A \to B\) に関して、集合 \(A\) 上で異なる要素の像が必ず \(B\) 上の異なる要素に対応する写像は単射 (injection) である。従って集合 \(B\) の位数は \(A\) と同じかそれより大きくなければならず \(f\) の像は \(B\) の部分集合となる。

写像 \(f:A \to B\) による像が \(B\) のすべての要素に対応する (像が \(B\) と等しい) 写像は全射 (surjection) である。従って集合 \(B\) の位数は \(A\) と同じかそれより小さくなければならない。

単射であり全射でもある写像を全単射 (bijection) と呼ぶ。全単射では集合 \(A\) と \(B\) は同じ位数を持ち、逆写像 \(f^{-1}\) が存在する。

準同形写像・同型写像

ある群 \((A, \ast)\) 上の要素 \(x_1, x_2, x_1 \ast x_2 \in A\) に対して \(f(x_1) \ast f(x_2) = f(x_1 \ast x_2)\) が成り立つ写像 \(f\) を準同型写像 (homomorphism) と呼ぶ。

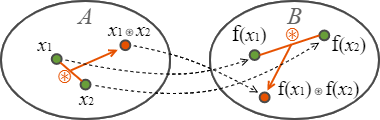
また準同型写像であり全単射である写像は同型写像 (isomorphism) である。単射で準同型の写像を単準同型写像、全射で準同型の写像を全準同型写像

線形性・双線形性・多重線形性

一つの変数 \(x\) を取る写像 \(f\) が以下の 2 つの性質を満たすとき \(f\) は線形性 (linearity) を持つ^[1]。

加法性または重ね合わせ: 任意の \(x,y\) に対して \(f(x + y) = f(x) + f(y) \)
同次性: 任意の \(a,x\) に対して \(f(ax) = af(x)\)

加法性と同次性を組み合わせることで \(f(ax + by) = af(x) + bf(y)\) と表すこともできる。双線形性は単純な線形性を 2 つの変数に拡張した性質である。\[ \begin{eqnarray*} f(x_1 + x_2,y) & = & f(x_1,y) + f(x_2,y) \\ f(x,y_1 + y_2) & = & f(x,y_1) + f(x,y_2) \\ f(ax,y) & = & f(x,ay) = af(x,y) \end{eqnarray*} \] このような性質を持つ写像 \(f\) を双線形写像と言う。

同様に多重線形性は \(n\) 個の変数に拡張したバージョンである。

双線形写像

体 \(K\) 上の線形空間 \(\mathbb{V}\), \(\mathbb{W}\), \(\mathbb{Z}\) に対して、写像 \(f:\mathbb{V} \times \mathbb{W} \to \mathbb{Z}\) がそれぞれの変数に対して \(K\) 線形であるとき、すなはち \[ f(av_1+bv_2,w) = af(v_1,w) + bf(v_2,w), \ \ a,b \in K, v_1, v_2 \in \mathbb{V}, w \in \mathbb{W} \\ f(v,aw_1+bw_2) = af(v,w_1) + bf(v,w_2), \ \ a,b \in K, v \in \mathbb{V}, w_1,w_2 \in \mathbb{W} \] が成り立つとき \(f\) は双線形写像であると言う。特に \(\mathbb{Z}\) が \(\mathbb{K}\) であるとき、\(f\) は双線型形式 (bilinear form) と言う。双線形写像 \(\mathbb{V}\times\mathbb{W}\to\mathbb{Z}\) とテンソル積 \(\mathbb{V}\otimes\mathbb{W}\) から \(\mathbb{Z}\) への線形写像は一対一に対応する。