組み合わせ

論文翻訳: Ranking and unranking permutations in linear time

Takami Torao 2001年の論文 #順列
  • このエントリーをはてなブックマークに追加

Wendy Myrvold1, Frank Ruskey*,2
Department of Computer Science, University of Victoria, Victoria, B.C. V8W 3P6, Canada
Received 17 April 2000; received in revised form 31 October 2000
Communicated by F.Y.L. Chin

Abstract

\(n\) 個の記号の順列に対するランク関数 (ranking function) は、\(n!\) 個の順列それぞれに \([0,n!-1]\) の範囲の一意の整数を割り当てる。対応するアンランク関数 (unranking function) はその逆で、\(0\) から \(n!-1\) までの整数が与えられたとき、関数の値はそのランクを持つ順列になる。我々は \(O(n)\) の算術演算で計算できる順列の簡単なランクまたはアンランクアルゴリズムを提示する。

Keywords: 順列 Permutation; ランク Ranking; アンランク Unranking, アルゴリズム Algorithms; 組み合わせ問題 Combinatorial problems

Table of Contents

  1. Abstract
  2. 1. ランクとアンランク
  3. 2. 可能な拡張
  4. References
  5. 翻訳抄

\(n\) 次の順列は \(n\) 個のシンボルの配置である。この論文ではモジュラー演算を適用する際の便宜上、\(\{0,1,2,\ldots,n-1\}\) の順列について検討する。\(\{0,1,2,\ldots,n-1\}\) のすべての順列の集合は \(S_n\) と表記する。

\(S_n\) の順列でインデックス付けされた配列を必要とするアプリケーションは数多くある [2]。一つの例は特定の種類の Cayley グラフのハミルトンサイクルを探索するプログラムの開発である [10, 11]。このようなインデックス付けを行うには、順列 \(\pi\) を入力とし、\(0,1,\ldots,n!-1\) 範囲の数 \(r(\pi)\) を生成する全単射ランク関数 (bijective ranking runction) \(r\) が必要である。\(r\) の逆関数もしばしば有用でありアンランク関数 (unranking function) と呼ばれる。

この問題に対する従来のアプローチは、まず順列の順序を定義し、次のその順序に対するランク関数とアンランク関数を見つけることである。例えば辞書式順序 (lexicographic order) での順列のランクは、単に辞書式順序でその順列に先行する順列の数に過ぎない。辞書式順序のランク関数とアンランク関数の単純な実装では \(O(n^2)\) 時間が必要である [7, 9]。

順列 \(\pi=\pi_0 \pi_1 \ldots \pi_{n-1}\) が与えられたとき、その逆転ベクトル (inversion vector) \(v=v_0 v_1 \ldots v_{n-1}\) の \(v_i\) は \(j \lt i\) において \(\pi_j \gt \pi_i\) となるエントリ \(\pi_j\) の数を表している。Hall ([12, p.203] 参照）はこの逆転ベクトルが順列を一意に決定することを最初に観測した。

辞書式順序で順列をランクやアンランクするより洗練されたアルゴリズムは中間ステップとして逆転ベクトルを計算する。ランクの最初のステップは順列の逆転ベクトルを決定することである。残念ながら素朴な実装では \(O(n^2)\) の時間がかかり、モジュラー演算 [5, Ex.6, p.18] やマージソート [5, Ex.21, p.168] を用いた \(O(n \log n)\) の実装でさえも遅すぎる。アンランクの最後のステップはその逆転ベクトルから順列を決定することである。ここでも素朴なアプローチでは \(O(n^2)\) 時間がかかる。平衡二進探索木を使用するとこれを \(O(n \log n)\) に改善できる。Dietz [3] の複雑なデータ構造を使えば実行時間を \(O((n \log n)/(n\log \log n))\) に短縮できるが、このアルゴリズムの実装は知られていない。逆転ベクトルとランク間の変換は簡単で \(O(n)\) の算術演算で実行できる、つまりボトルネックは順列とその逆転ベクトル間の変換である。

辞書式順序で順列をランク付けする問題全体は、順列の版点数を計算する問題と密接に絡み合っており、この計算を線形時間で行うには、それが可能だとしても、大きなブレイクスルーが必要であるように思われる。我々の新しいアルゴリズムは順列が辞書式順序になっていることを要求しないことで線形時間を達成している。

我々の順列ランクアルゴリズムは、例えば Steinhaus-Johnson-Trotter 順序などで公開されているが、これらは辞書的アルゴリズムに比べて実行時間の利点を提供しない。これらのアルゴリズムの説明については Reingold, Nievergelt, Deo [9] や Kreher と Stinson [6] を参照。

この問題に対する我々のアプローチは 2 つの点で以前のアプローチとは異なる。まず、順列の順序を選択してからそれに対応するランクアルゴリズムとアンランクアルゴリズムを見つけるのではなく、順序はアンランクアルゴリズムによって定義され、それは特に説明が簡単ではない。二つ目の違いは、まずアンランクアルゴリズムが開発され、それからランクアルゴリズムが導き出されることである。従来はまずランクアルゴリズムが開発されてからアンランクアルゴリズムが開発されてきた。さらに、我々が知っている他のすべてのケースでは、アンランクアルゴリズムはランクアルゴリズムより複雑だが ─ ここはそうではない!

  1. *共著者. E-mail アドレス: wendym@csr.uvic.ca (W. Myrvold), fruskey@csr.uvic.ca (F. Ruskey).
  2. 1研究の一部は NSERC 助成金 OGP0041927 の支援を受けている。
  3. 2研究の一部は NSERC 助成金 OGP0003379 の支援を受けている。

1. ランクとアンランク

このセクションではランクとアンランク順序について少し異なる 2 つのアプローチを紹介する。最初のアプローチ (rank1 と unrank1) はよりシンプルなコードである。二つ目のアプローチ (rank2 と unrank2) は順列のランクによる順序付けが理解しやすいために含まれている。。

我々の着想は、ランダムな順列を生成するための標準的なアルゴリズム [8, 4, 1] である。配列 \(\pi[0..n-1]\) は恒等順列 (identity permutation) (またはその他の順列) に初期化され、次のループが実行される:

1. \( {\bf for} \ k := n-1, n-2, \ldots, 1 \ {\bf do} \)
2. \( \hspace{12pt}{\it swap}(\pi[k], \pi[{\it rand}(k)]); \)

ここで \({\it rand}(k)\) の呼び出しは \(0..k\) の範囲のランダムな整数を生成する必要がある。

このアルゴリズムは \(S_n\) のすべての順列の中から一様にランダムに選ばれた順列を生成する。\(r_{n-1},\ldots,r_1,r_0\) をアルゴリズムによって生成されたランダム要素のシーケンスとする。ここで \(0 \le r_i \le i\) である。このようなシーケンスは \(n(n-1)(n-2)\cdots2\cdot 1=n!\) 個存在するため、異なるシーケンスはそれぞれ異なる順列を生成しなければならない。したがって \(0..n!-1\) 範囲内の整数 \(r\) (訳注: ランク) を取り、それを \(r_{n-1},\ldots,r_1,r_0\) の値の一意なシーケンスに変えることができればアンランクができるはずである。ここで \(0 \le r_i \le i\) である。詳細は以下を参照。

順列をアンランクするにはまず \(\pi\) を恒等順列として初期化する: \(\pi[i] := i\) for \(i = 0,1,\ldots,n-1\)

1. \( {\bf procedure} \ {\it unrank1}(n,r,\pi) \)
2. \( \hspace{12pt}{\bf if} \ n \gt 0 \ {\bf then} \)
3. \( \hspace{24pt}{\it swap}(\pi[n-1], \pi[r \bmod n]); \)
4. \( \hspace{24pt}{\it unrank1}(n-1, \lfloor r/n \rfloor, \pi); \)
5. \( \hspace{12pt}{\bf fi} \)
6. \( {\bf end} \ \{{\rm of} \ {\it unrank1}\}; \)

この関数が機能する理由は明らかだろう。上で言及した議論を使うこともできるし、次のように直接議論することもできる。我々は \(S_n\) のすべての順列がある \(r \in \{0,1,\ldots,n!-1\}\) に対して可能な結果であることを示せば良い。明らかに \(\pi[0..n-1]\) のすべての可能な値は交換後の位置 \(n-1\) に出現することができる。\(\pi[n-1]\) が設定された後はそれが再び変更されることはない。さらに、\[ \left\{ \left\lfloor \frac{r}{n} \right\rfloor: r \in \{0,1,\ldots,n!-1\} \right\} = \{0,1,\ldots,(n-1)!-1\} \] であるため、機能的に \(\pi[0..n-2]\) のすべての可能な順列が発生する可能性があると想定できる。

ランク付けするにはまず \(\pi^{-1}\) を計算する。これは \(i=0,1,\ldots,n-1\) に対して \[ \pi^{-1} \left[ \pi[i] \right] := i \] を反復することにより \(O(n)\) 操作で実行できる。以下のアルゴリズムでは \(\pi\) と \(\pi^{-1}\) の両方が修正される。

1. \( {\bf function} \ {\it rank1}(n, \pi, \pi^{-1}):\ {\rm integer}; \)
2. \( \hspace{12pt}{\bf if} \ n = 1 \ {\bf then} \ {\rm RETURN}(0) \ {\bf fi}; \)
3. \( \hspace{12pt}s := \pi[n-1]; \)
4. \( \hspace{12pt}{\it swap}(\pi[n-1], \pi[\pi^{-1}[n-1]]); \)
5. \( \hspace{12pt}{\it swap}(\pi^{-1}[s], \pi^{-1}[n-1]); \)
6. \( \hspace{12pt}{\rm RETURN}(s+n \cdot {\it rank1}(n-1, \pi, \pi^{-1})); \)
7. \( {\bf end} \ \{{\rm of} \ {\it rank1}\}; \)

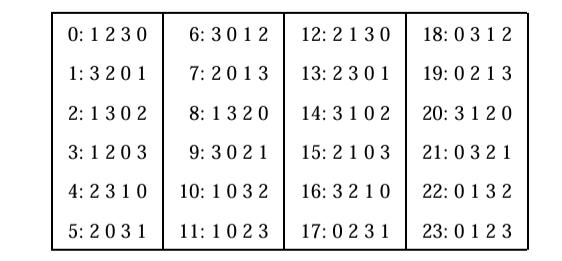
これらのアルゴリズムは明らかに \(O(n)\) の演算を使用する。\(n=4\) の場合の順列に対応するランクは Fig 1 に示されている。

ここで、最初のアルゴリズムとは異なるが、同じ基本原理に基づく別のアンランクアルゴリズムを紹介する。このアルゴリズムでは、順列は異なる順序で発生し、最初のアルゴリズムによって生成される順序よりも記述しやすい順序となる。unrank2 を呼び出す前に、\(i=0,1,\ldots,n-1\) に対して \(\pi[i]:=i\) となるような恒等順列として \(\pi\) を初期化する。rank2 を呼び出す前に \(\pi^{-1}\) を計算する。

1. \( {\bf procedure} \ {\it unrank2}(n, r, \pi) \)
2. \( \hspace{12pt}{\bf if} \ n \gt 0 \ {\bf then} \)
3. \( \hspace{24pt}s := \lfloor r/(n-1)! \rfloor; \)
4. \( \hspace{24pt}{\it swap}(\pi[n-1], \pi[s]); \)
5. \( \hspace{24pt}{\it unrank2}(n-1, r \bmod (n-1)!, \pi); \)
6. \( \hspace{12pt}{\bf fi}; \)
7. \( {\bf end} \ \{{\rm of} \ {\it unrank2}\}; \)
1. \( {\bf function} \ {\it rank2}(n, \pi, \pi^{-1}): \ {\rm integer}; \)
2. \( \hspace{12pt}{\bf if} \ n = 1 \ {\bf then} \ {\rm RETURN}(0) \ {\bf fi}; \)
3. \( \hspace{12pt}s := \pi[n-1]; \)
4. \( \hspace{12pt}{\it swap}(\pi[n-1], \pi[\pi^{-1}[n-1]]); \)
5. \( \hspace{12pt}{\it swap}(\pi^{-1}[s], \pi^{-1}[n-1]); \)
6. \( \hspace{12pt}{\rm RETURN}(s \cdot (n-1)! + {\it rank2}(n-1, \pi, \pi^{-1})); \)
7. \( {\bf end} \ \{{\rm of} \ {\it rank2}\}; \)

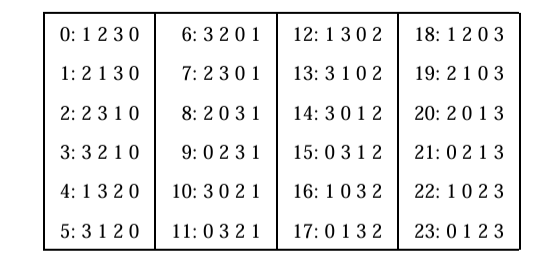
\(n=4\) の場合の生成順序を Fig 2 に示す。一般にこの順序は次のように記述できる。\(\mathcal{L}_n\) を \(0..n-1\) の順列のリストとする。\(\mathcal{L}_n^m\) は \(\mathcal{L}_n\) のリストを示すが、\(m\) のすべての出現が \(n\) に置き換えられるものとする。このとき \[ \mathcal{L}_{n+1} = \mathcal{L}_n^0 \cdot 0 \circ \mathcal{L}_n^1 \cdot 1 \circ \cdot \circ \mathcal{L}_n^{n-1} \cdot (n-1) \circ \mathcal{L}_n^n \cdot n \] である。例えば Fig 2 の最後の列はリスト \(\mathcal{L}_3^3\cdot 3=\mathcal{L}_3 \cdot 3\) である。\(\circ\) はリストの連結を表し、表記 \(\mathcal{L}\cdot x\) はリスト \(\mathcal{L}\) 内のすべての順列の末尾に文字 \(x\) を追加することを意味する。

Fig 1. rank1, \(n=4\) の順列のランク。
Fig 2. rank2, \(n=4\) の順列のランク。

2. 可能な拡張

ランダムな順列を生成するアルゴリズムが \(k\) 番目のステップで終了する場合、位置 \(n-k..n-1\) のランダムな \(k\)-順列を保持する。したがって我々のランクとアンランクアルゴリズムは \(n\)-セットの \(k\)-順列を行うように簡単に変更できる。

References

  1. G. de Balbine, Note on random permutations, Math. of Comput. 21 (1967) 710–712.
  2. F. Critani, M. Dall’Aglio, G. Di Biase, Ranking and unranking permutations with applications, in: Innovation in Mathematics (Rovaniemi, 1997), Comput. Mech., Southampton, 1997, pp. 99–106.
  3. P.F. Dietz, Optimal algorithms for list indexing and subset rank, in: Workshop on Algorithms and Data Structures (WADS), Lecture Notes in Comput. Sci., Vol. 382, Springer, Berlin, 1989, pp. 39–46.
  4. R. Durstenfeld, Algorithm 235: Random permutation, Comm. ACM(1964) 420.
  5. D.E. Knuth, The Art of Computer Programming, Vol. 3: Sorting and Searching, 2nd edn., Addison-Wesley, Reading, MA, 2000 (first published in 1973).
  6. D.L. Kreher, D.R. Stinson, Combinatorial Algorithms: Generation, Enumeration, and Search, CRC Press, Rockville, MD, 1999.
  7. J. Liebehenschel, Ranking and unranking of lexicographically ordered words: An average-case analysis, J. Automat. Languages Combinatorics 2 (1997) 227–268.
  8. L.E. Moses, R.V. Oakland, Tables of Random Permutations, Stanford University Press, Stanford, CA, 1963.
  9. E.M. Reingold, J. Nievergelt, N. Deo, Combinatorial Algorithms: Theory and Practice, Prentice-Hall, Englewood Cliffs, NJ, 1977.
  10. F. Ruskey, M. Jiang, A. Weston, The Hamiltonicity of directed \(\omega\)-\(\tau\) Cayley graphs (or: A tale of backtracking), Discrete Appl. Math. 57 (1) (1995) 75–83.
  11. F. Ruskey, C. Savage, Hamilton cycles that extend transposition matchings in Cayley graphs of \(S_n\), SIAM J. Discrete Math. 6 (1) (1993) 152–166.
  12. C.B. Tompkins, Machine attacks on problems whose variables are permutations, in: Numerical Analysis, Proceedings of Symposia in Applied Mathematics, Vol. 6, American Mathematical Society, Providence, RI, 1956.

翻訳抄

順列を識別する一意な整数を計算する「ランク」と、順列のランクに基づいて並びを生成する「アンランク」を効率的に行うアルゴリズムを提案する 2001 年の論文。従来の方法では \(O(n \log n)\) 時間がかかることが多いが、この論文で紹介されている手法では事前計算された階乗を利用して \(O(n)\) の線形時間実行できるようにしている。

  1. MYRVOLD, Wendy; RUSKEY, Frank. Ranking and unranking permutations in linear time. Information Processing Letters, 2001, 79.6: 281-284.