有効数字
 定義と性質
定義と性質
有効数字 (significant figures of number) は実数の分解能を意味する数字。数値のどの桁までが意味を持つかを表している。
例えばある数値 \(t=1.234\times 10^{-2}\) は数学的に \(1.234000\ldots\times 10^{-2}\) と等値だが、計測値として扱う場合は末尾が四捨五入されて 4 になったことを暗に意味している。つまり数直線上の点ではなく範囲であることを表している。\[ 1.2335\times 10^{-2} \leq t \lt 1.2345\times 10^{-2} \] 上記を有効数字4桁の数値と呼ぶ。有効数字より後の桁は不確実で意味がないため表記しないが、有効数字内の桁であれば 0 であっても表記しなければならない。以下に例を示す。
| \(1.23\) | 有効数字3桁 |
| \(12.34\) | 有効数字4桁 |
| \(123.0\) | 有効数字4桁 |
| \(1.230\times 10^{-3}\) | 有効数字4桁 |
| \(0.001230\) | 有効数字4桁。 |
| \(12300\) | 有効数字3~5桁ととれて曖昧。 より正確に \(1.230\times 10^4\) のように表記する。 |
有効数字は実数演算を行う上で浮動小数点演算の精度と関係する。
 計測値
計測値
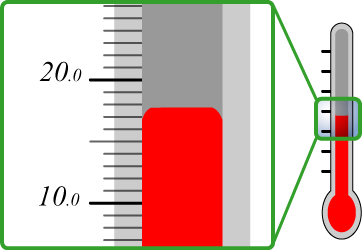
アナログメーターの計測機器は目盛りの 1/10 までを有効数字として読み取りを行う。例えば Fig.1 の温度計は 17.0℃ と 18.0℃の間を示していることは確実である。読み取りの計測値はおおむね 17.8℃ だろう。つまりこの温度計から得られた温度の有効数字は 3 桁である (最後の桁は目分量による曖昧さを含んでいる)。デジタルメーターの計測機器でも最後の桁は曖昧さを含んでいるものとして扱う。
ここで 17.80 ℃と表記された温度とは有効数字が異なることに注意。17.80℃ とは分解能が10倍の温度計を使用したときに得られる計測値で、小数点第2位までが有効であることを示している。表記の違いが暗示する有効数字が異なるため数値の末尾に意味なく 0 を追加したり、末尾の 0 を削除しない。
 有効数字を伴う演算
有効数字を伴う演算
有効数字を持つ数値の演算では、曖昧さを含む桁が演算に関与した桁も曖昧さを含むものとして考える (ただし繰り上がった桁を除く)。最終的に曖昧な桁の中で最も大きい桁のみを残すように四捨五入を行う。これは四則演算において以下のルールとなる。
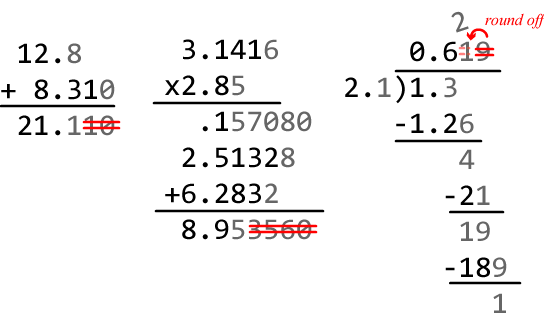
加減算は末尾桁が大きい側の桁にあわせる。12.8 + 8.310 の末尾桁が大きい方の桁は小数点第1位であるため結果は 21.110 \(\approx\) 21.1 となる。乗除算は有効数字が少ない側の有効数字にあわせる。3.1416×2.85 の有効数字が少ない方の有効数字は 3 であるため結果は 8.953560 \(\approx\) 8.95 となる。
この方法は実験計測において用いられる手法である。工業製品では JIS 規格によって別に四捨五入の手順が定められている。