基本的な用語と方程式

確率の式

確率変数

不確定な量。サイコロの目やコインの裏表、温度など。

確率密度関数

確率密度関数 (probability density function; PDF) \(f\) は連続確率変数 \(x\) が \((x_0,x_1)\) 区間に含まれる確率を以下のように表すことのできる関数である。\[ P(x_0 \lt x \lt x_1) = \int_{x_0}^{x_1} f(x) dx \]

\(x\) の定義域 (取りうる区間) を \((t_0,t_1)\) とするとき、その全域で積分すると \(\int_{t_0}^{t_1} f(x) dx = 1\) を得る。一般的に \(x\) の定義域外では 0 を取るとし以下のように表す。\[ \int_{-\infty}^\infty f(x) dx = 1 \]

値域は \(f(x) \geq 0\) であるが、確率は面積で表されることから \(f(x)\) が 1 を超えることもあることに注意。

確率密度関数の不定積分は累積分布関数 (cumulative distribution function; CDF) である。\[ F(x) = \int_{-\infty}^x f(t) dt, \ \ f(x) = \frac{d F(x)}{dx} \]

条件付き確率

同時確率 (simultaneous probability) または結合確率 (joint probability) は事象 \(x\) と \(y\) がどちらも観測される確率。\(P(x, y)\) または \(P(x \cap y)\) で表される。同時確率の事象 \(x\) と \(y\) が互いに独立であればそれぞれの確率の積で表すことができる。\[ P(x, y) = P(x) P(y) \]

条件付き確率 (conditional probability) は同時確率の特定の確率変数を固定したときの確率。事象 \(x=x_1\) が起きる上で \(y\) が起きる確率は以下のように表される。\[ P(y|x=x_1) = \frac{P(x,y)}{P(x_1)} \] 事象 \(x\) と \(y\) が互いに独立のとき \(P(y|x) = P(y)\) である。

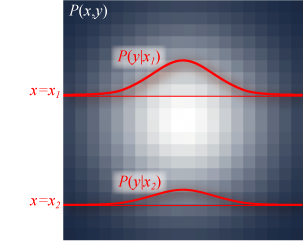
右図のように、条件付き確率は同時確率に対する断面となる分布に相当するが、確率密度関数とするには積分して 1 となるよう正規化を行わなければならない。\[ \begin{align*} P(y|x=x^*) & = \frac{P(y,x=x^*)}{\int P(y,x=x^*)dy} \\ & = \frac{P(y,x^*)}{P(x=x^*)} \end{align*} \] これをより簡略に以下のように記述する。\[ \begin{equation} P(y|x) = \frac{P(x,y)}{P(x)} \label{conditional_probability} \end{equation} \] 式 (\(\ref{conditional_probability}\)) は \(x\) が特定の値に固定されたときの \(y\) の確率分布である。またこの式により同時確率を条件付き確率として表すことができる。\[ \begin{equation} P(x,y)=P(x|y)P(y) \label{jointed_prob_for_cond} \end{equation} \] 式 (\(\ref{jointed_prob_for_cond}\)) を使用して複数の確率変数を持つ同時確率を条件付き確率に分解することができる。\[ \begin{align*} P(w,x,y,z) & = P(w,x,y|z) P(z) \\ & = P(w,x|y,z) P(y|z) P(z) \\ & = P(w|x,y,z) P(x|y,z) P(y|z) P(z) \end{align*} \]

周辺確率

周辺確率 (marginal probability) は同時確率の確率を合計した確率。同時確率 \(P(x,y)\) が与えられたとき以下の式で \(x\), \(y\) それぞれの確率分布が求められる。\[ \begin{align*} P(x) & = \int P(x,y) dy \\ P(y) & = \int P(x,y) dx \end{align*} \] 離散分布の場合は以下のように求める。\[ \begin{align*} P(x) = \sum_y P(x,y) \\ P(y) = \sum_x P(x,y) \end{align*} \] ベイズ推定で同時分布を扱うとき、変数を消去して周辺分布を求めることはよく行われる。