ベイズの定理

\(P(A \cap B)\) は \(P(A|B)\times P(B)\) と等しく、また \(P(B|A) \times P(A)\) とも等しい。\[ P(A \cap B) = P(A) \times P(B|A) = P(B) \times P(A|B) \]

これを変形してベイズの定理を得られる。\[ \begin{equation} P(B|A) = \frac{P(A|B) P(B)}{P(A)} \label{bayes_theorem} \end{equation} \]

事後分布 \(P(B|A)\)

機械学習では \(P(p|x)\) つまりデータからその生起確率の確率分布を表している。

尤度関数 \(P(A|B)\)

機械学習では \(P(x|p)\) つまり得られたデータが従った生起確率の分布を現している。

事前分布 \(P(B)\)

機械学習では \(P(p)\) つまり生起確率が従った確率分布を表している。

エビデンス (周辺尤度) \(P(A)\)

事後分布が確率密度関数となることを保証するための正規化定数。機械学習では \(P(x)\) つまり

周辺化によって、連続の場合 \[ P(A) = \int P(A, B) dB = \int P(A|B)P(B) dB \]、離散の場合 \[ P(A) = \sum p(A, B) = \sum P(A|B) P(B) \] と展開することができる。

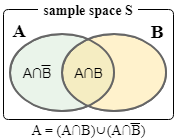右図より \[ \begin{align*} P(A) & = P(A \cap B) + P(A \cap \bar{B}) \nonumber \\ & = P(B) \times P(A|B) + P(\bar{B}) \times P(A|\bar{B}) \end{align*} \] したがって以下のように書くこともできる。\[ \begin{equation} P(B|A) = \frac{P(A|B) P(B)}{P(B) \times P(A|B) + P(\bar{B}) \times P(A|\bar{B})} \label{bayes_by_set} \end{equation} \]

偽陽性問題

問題 : ある臨床検査は 病気にかかっている \({}_{[B]}\) 人が受けると 99% の確率 \({}_{[P(A|B)=0.99]}\) で 陽性 \({}_{[A]}\) と出る。ただし 病気にかかっていない \({}_{[\bar{B}]}\) 人が受けても 5% の確率 \({}_{[P(A|\bar{B})=0.05]}\) で陽性と出る。ここで陽性が出たとしても実際にその病気にかかっている人は 全体の 0.1% \({}_{[P(B)=0.0001]}\) である。ある人が陽性の判定を受けたとき、実際に 病気にかかっている確率 \({}_{[P(B|A)]}\) を求めよ。

ベイズの定理 (\(\ref{bayes_by_set}\)) より: \[ \begin{align*} P(B|A) & = \frac{0.99 \times 0.0001}{0.0001 \times 0.99 + 0.9999 \times 0.05} \\ & = 0.00197628458 \end{align*} \]