システム稼働率
 概要
概要
システム稼働率 (system availability factor) はシステムに期待できる可用性の指標である。
Table of Contents
 稼働率
稼働率
稼働率は、システムが継続して機能する平均時間を意味する平均故障間隔 (MTBF; mean time between failures) と、システムに障害が発生してから復旧するまでの平均時間を意味する動作不能時間 (MTTR; mean time to recovery) を使用して式 (\(\ref{a_factor}\)) のように表すことができる。\[ \begin{equation} P = \frac{\rm MTBF}{{\rm MTBF} + {\rm MTTR}} \label{a_factor} \end{equation} \]
大雑把だが、システム稼働率は年間の停止時間に換算すると把握しやすい (MTBF が機能継続した時間を意味しているため必ずしも正しくはないが)。例えば稼働率 \(P=0.99\) のシステムは Table 1 が示すように 1 年間で87時間半程度の停止時間が予想されることを示している。
この記事では稼働率が設定されている機器やサブシステムを接続したとき、システム全体としてどのような稼働率になるかの計算方法を説明する。
| 稼働率 | 年間停止時間 |
|---|---|
| 0.99 | 3日と15時間36分 |
| 0.999 | 8時間45分 |
| 0.9999 | 52分34秒 |
| 0.99999 | 5分15秒 |
| 0.999999 | 32秒 |
 直列接続と並列接続
直列接続と並列接続
稼働率 \(p_1,p_2,\ldots,p_n\) を持つ \(n\) 個の機器 (サブシステム) で構成されるシステムを想定する。もしそれらの機器の 1 つでも停止するとシステム全体が機能しなくなるのであれば、そのシステムの稼働率 \(P\) は全ての機器の稼働率の積として式 (\(\ref{serial}\)) のように表すことができる。\[ \begin{equation} P = p_1 \times p_2 \times \ldots \times p_n \label{serial} \end{equation} \]
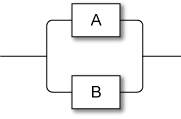
一方で、\(n\) 個の機器の中で 1 つでも機能していればシステム全体が機能するのであれば、そのシステムの駆動率は式 (\(\ref{parallel}\)) のように表すことができる。\[ \begin{equation} P = 1 - (1 - p_1) (1 - p_2) \ldots (1 - p_n) \label{parallel} \end{equation} \] 式 (\(\ref{parallel}\)) は「全てが停止する確率 + 1つ以上が機能している確率 = 1」という考えに基づいた算法である。つまり 100% から全ての機器が停止する確率を減算することで 1 つ以上の機器が機能している状態の確率を算出している。
このような構成は基本情報技術者試験やシスアド試験において Fig 1 のような「直列接続」「並列接続」のモデルで頻出される問題である。

 \(f\)-\(n\) 稼働率
\(f\)-\(n\) 稼働率
前述の並列接続で扱うケースでは \(n\) 個の機器のうち 1 つが機能していればシステム全体が機能するという暗黙の前提があった。しかし高可用性を目的とする現実なシステムではより複雑な構成を取ることが多い。これは、例えば 4 個のディスクアレイのうち 2 個までの故障を許容できる RAID-6 システムや、7 ノードクラスタのうち 3 ノードの障害までを許容可能な分散データベースなどを対象とするケースである。より一般的な問題として以下の表現に置き換えられる。
\(n\) 個の機器で構成され、そのうち最大 \(f\) 個の機器が停止しても機能を継続することができるシステムの稼働率 \(P\) を求める。
このようなケースでは、システム全体の稼働率 \(P\) は (\(\ref{P_based_on}\)) のように 0 個から \(f\) 個の機器が停止する確率の合計で求める必要がある。\[ \begin{equation} P = \sum_{i=0}^f (\mbox{$n$ 個のうち $i$ 個が故障する確率}) = \sum_{i=0}^f P_i \label{P_based_on} \end{equation} \] これは基本情報技術者試験での並列接続のアプローチとは異なることに注意 (例1参照)。
 すべての機器の稼働率が同一のケース
すべての機器の稼働率が同一のケース
まずすべての機器が同じ駆動率 \(p\) を持つケースについて考える。\(n\) 個の機器のうち \(i\) 個が故障する確率 \(P_i\) を順に求めてみよう。
\(i=0\) のケース、つまり一つの機器も停止していない状態となる確率はすべての機器の稼働率の積で表すことができる。これは、すべての機器が同じ稼働率であることから \(P_0=p^n\) となる。\[ P_{i=0} = p_1 \times p_2 \times \ldots \times p_n = p^n \] \(i=1\) のケース、つまり全体で 1 個の機器のみが停止している状態は、例えば \(n=3\) であれば「001」「010」「100」のように二項係数を使って \(\binom{3}{1}=3\) 通りの組み合わせが存在し、それぞれの組み合わせの生起確率の和で表すことができる。\[ P_{i=1} = \sum_{j=1}^n \underbrace{p_1 \times \ldots \times p_n}_{\mbox{except } p_j} \times (1-p_j) = \binom{n}{1} p^{n-1} (1-p) \] \(i=2\) のケース、つまり全体で 2 個の機器が停止している状態は \(\binom{n}{2}\) 通りが存在する。\[ P_{i=2} = \sum_{j=1}^n \sum_{k=j+1}^n \underbrace{p_1 \times \ldots \times p_n}_{\mbox{except } p_j, p_k} \times (1-p_j) (1-p_k) = \binom{n}{2} p^{n-2} (1-p)^2 \] 一般化した \(P_{i=f}\) のケースは \(\binom{n}{f}\) 通りが存在する。\[ \begin{eqnarray} P_{i=f} & = & \sum_{j=1}^n \sum_{k=j+1}^n \ldots \sum_{z=y+1}^n \underbrace{p_1 \times \ldots \times p_n}_{\mbox{except } p_j, p_k, \ldots, p_z} \times (1-p_j) (1-p_k) \ldots (1-p_z) \label{p_diff_general} \\ & = & \binom{n}{f} p^{n-f} (1-p)^f \label{p_same_general} \end{eqnarray} \]
式 (\(\ref{p_same_general}\)) より、すべての機器が同一の稼働率 \(p\) で表される状況でのシステム全体の稼働率 (\(\ref{P_based_on}\)) は式 (\(\ref{p_same}\)) のように表すことができる。\[ \begin{equation} P = \sum_{i=0}^f \left\{ \binom{n}{i} p^{n-i} (1-p)^i \right\} \label{p_same} \end{equation} \] ここで \(\binom{n}{0}=1\) とする。
 個々の機器の稼働率が異なるケース
個々の機器の稼働率が異なるケース
より一般的なケースとして個々の機器の駆動率が異なる場合について考える。これは組み合わせの選択ごとに生起確率が異なるため「確率×組み合わせ数」で単純化することができない。式 (\(\ref{p_diff_general}\)) をシステム全体の稼働率 (\(\ref{P_based_on}\)) に適用すると式 (\(\ref{p_diff}\)) のように表される。\[ \begin{equation} P = \sum_{i=0}^f \left\{ \underbrace{\sum_{j \in [1,n]} \sum_{k \in [j+1,n]} \ldots \sum_{z \in [y+1,n]}}_{i\times \ \mbox{multiplex}} \underbrace{p_1 \times \ldots \times p_n}_{\mbox{except } p_j, p_k, \ldots, p_z} \times (1-p_j) (1-p_k) \ldots (1-p_z) \right\} \label{p_diff} \end{equation} \] 式 (\(\ref{p_diff}\)) は組み合わせを表すために叙述的な表現をしており、数式としてはいささか正確さに欠けるため、以下に式 (\(\ref{p_diff}\)) が意味するところをコードで補足する。
import itertools
def availability_factor(p, f):
P = 0
for i in range(f + 1):
for fails in itertools.combinations(range(len(p)), i):
px = 1.0
for ii in range(len(p)):
px *= p[ii] if ii not in fails else (1.0 - p[ii])
P += px
print("P[%d]+=%f, fails=%s" % (i, px, fails))
return P
print("P=%f" % availability_factor([0.9, 0.8, 0.6], 2))
# P[0]+=0.432000, fails=()
# P[1]+=0.048000, fails=(0,)
# P[1]+=0.108000, fails=(1,)
# P[1]+=0.288000, fails=(2,)
# P[2]+=0.012000, fails=(0, 1)
# P[2]+=0.032000, fails=(0, 2)
# P[2]+=0.072000, fails=(1, 2)
# P=0.992000
itertools.combinations(range(n), k) は n 個の集合から k の要素を選ぶときのすべての組み合わせを列挙する機能である。上記のコードではシステムが許容可能な停止パターンのすべて (一つも停止していないケースを含む) を列挙し、各生起確率の総和を算出している。
 例1: 並列接続問題
例1: 並列接続問題
基本情報技術者試験で扱う並列接続問題を例に考えてみよう。前述の通り、それらは「システム内の機器の 1 つが機能していればシステム全体は機能する」と説明されていることから、式 (\(\ref{p_diff}\)) に対する \(f=n-1\) の特殊ケースと見なすことができる。
並列接続の稼働率に対して、一般的な基本情報技術者試験の解法では: \[ P = 1 - (\mbox{すべての機器が同時に停止する確率}) \] のアプローチで説明している。例えば駆動率 \(p_a=0.9\), \(p_b=0.8\), \(p_c=0.6\) の 3 つの機器 A, B, C を並列接続したシステムの駆動率は \(P=1-(1-p_a)(1-p_b)(1-p_c)\) より \(P=0.992\) である。
一方、式 (\(\ref{p_diff}\)) で \(n=3\), \(f=2\) となる解法を使用しても: \[ \begin{eqnarray*} P_0 & = & p_a p_b p_c = 0.432\\ P_1 & = & p_a p_b (1-p_c) + p_a (1-p_b) p_c + (1-p_a) p_b p_c = 0.444\\ P_2 & = & p_a (1-p_b) (1-p_c) + (1-p_a) p_b (1-p_c) + (1-p_a) (1-p_b) p_c =0.116\\ \therefore P & = & P_0 + P_1 + P_2 = 0.992 \end{eqnarray*} \] と同じ結果が得られる。
もう一つの例として、A, B, C 全ての機器が等しい稼働率 \(p=0.9\) を持つケースについて考える。基本情報技術者試験の解法では \(P=1-(1-0.9)^3=0.999\) である。一方で式 (\(\ref{p_same}\)) の解法を使用しても: \[ \begin{eqnarray*} P & = & \sum_{i=0}^2 \left\{ \binom{3}{i} 0.9^{3-i} (1-0.9)^i \right\} \\ & = & 0.9^3 + 3 \times 0.9^2 \times 0.1 + 3 \times 0.9 \times 0.1^2 \\ & = & 0.999 \end{eqnarray*} \] と同じ結果が得られる。
このように、一般化した解法と基本情報技術者試験の解法は異なるアプローチで同じ結果となるものの、前者のほうが圧倒的に複雑で計算量が多い。並列接続問題は状況を限定することで簡単な考え方で実用的な解答を導くことができるように配慮されたものである。
 例2: 直列接続問題
例2: 直列接続問題
式 (\(\ref{p_diff}\)) ではシステムで停止を許容できる機器の最大数が 0 のとき、システム全体の稼働率 \(P\) は全ての機器の稼働率の積で表される。これは直列接続と等価である。つまり、直列接続は \(f\)-\(n\) 稼働率における \(f=0\) の特殊ケースと見なすことができる。
 例3:
例3:
Apache Cassandra で一貫性レベルに Quorum を指定すると (n-1)/2 + 1 ノードに
