制御理論
 概要
概要
自然に変化する系 (システム) に対して、系が目的の状態となるように系の変化率に作用する入力を外部から人為的に与えることを制御 (control) と呼ぶ。
Table of Contents
 導入
導入
ある状態予測モデルに基づいて (系の実際の出力を観測することなく) コントローラが入力を制御する方法をフィードフォワード制御 (feed forward control; 予測制御) または開ループ制御 (open loop control) と呼ぶ。一方で、系の実際の出力と参照値 (目標値) との差に基づいてコントローラがアクションを起こす制御をフィードバック制御 feedback control) または閉ループ制御 (closed loop control) と呼ぶ。参照値は時間によって変化する可能性があることに注意。
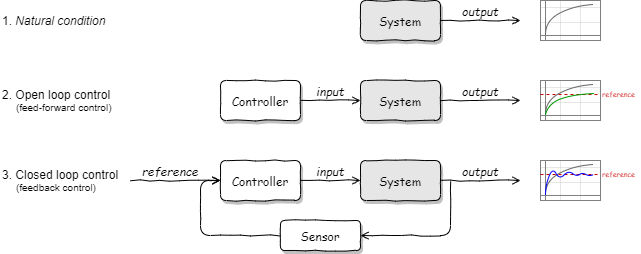
例えば 15 分でスイッチが切れる加熱を行う湯沸かし器や風呂釜は、水量に対して 15 分の加熱を行えば適温になるという状態予測モデルに基づいたフィードフォワード制御である。このような系の状態 (出力) の観測を行わないフィードフォワード制御では季節ごとの水温の違いを考慮しないため、冬場の屋外といった状況では適温にならない可能性がある。フィードバック制御の湯沸かし器は実際の湯温を計測しながら加熱時間を調整するため、より広い状況に適用することができる。
システムに対する入力と出力が微分方程式の関係で表されるシステムを動的システム (dynamical system) と呼ぶ。動的システムにおける出力は、過去の入力の時間変化の影響を受ける点で静的システムと異なる。
例として粘性のある平面に置いた物体に力を加えたときの運動について考える。粘性係数 \(c\)、物体の質量を \(m\)、加える力を \(f(t)\)、位置を \(x(t)\) としたとき、運動方程式は物体の速さ \(v=\frac{dx}{dt}\) に比例する粘性力の減衰項を含んだ微分方程式 (\(\ref{newton2}\)) で表される。\[ \begin{equation} m \frac{d^2x}{dt^2} = f(t) - c \frac{dx}{dt} \label{newton2} \end{equation} \] このように動的システムは古典力学や電気回路から経済や社会科学まで様々な分野で現れる。
 ラプラス変換
ラプラス変換
入力 \(x\) が系の出力 \(y\) にどのように作用するかを把握するためには系を \(y = f(x)\) 形式の式で表せるとよい。しかし微分方程式を直接的に解いて \(y\) の式を求めることは一般に困難である。ここでラプラス変換 (Laplace transform) を使って微分方程式を簡単な代数式に変換し、代数式を変形したあとに逆ラプラス変換で \(y\) の式に変換することができる。
時刻 \(t \ge 0\) で定義される実数値の関数 \(f(t)\) において式 (\(\ref{laplace}\)) で表される積分値 \(F(s)\) を \(f(t)\) のラプラス変換とする。\[ \begin{equation} F(s) = \mathcal{L}[f(t)] = \int_0^{\infty} f(t) \, e^{-st} dt \label{laplace} \end{equation} \] ここで \(s\) は複素数である。
典型的な原関数のラプラス変換は公式化されラプラス変換表という形で見つけることができる。例えば時間変数 \(f(t)\) に対する時間微分、時間積分のラプラス変換はそれぞれ式 (\(\ref{lap_dev}\)), (\(\ref{lap_int}\)) のように表される。\[ \begin{eqnarray} \mathcal{L} \left[ \frac{df(t)}{dt} \right] & = & s \, F(s) - f(0) \label{lap_dev}\\ \mathcal{L} \left[ \int_{0}^t f(t) \, dt \right] & = & \frac{1}{s} F(s) \label{lap_int} \end{eqnarray} \] また \(a_i\) を任意の定数、\(f_i(t)\) を任意の時間変数としたとき、ラプラス変換は式 (\(\ref{lap_linear}\)) に示すような線形性を持つ。\[ \begin{equation} \mathcal{L} \left[ a_1 f_1(t) + \dots + a_n f_n(t) \right] = a_1 F_1(t) + \ldots + a_n F_n(t) \label{lap_linear} \end{equation} \]
式 (\(\ref{newton2}\)) をラプラス変換すると以下のように表すことができる。\[ s^2 F(s) - s f(0) - \frac{df(0)}{dt} = \frac{1}{m} F(s) \]
 PID 制御
PID 制御
入力 \(x(t)\) に対して出力 \(y(t)\) 系について考える。
目標とする参照値 \(y_r(t)\) と実際の出力 \(y(t)\) との差 \(e(t)=y_r(t)-y(t)\) を偏差としたとき、現在の偏差 \(e\) を定数 \(K_p\) 倍したフィードバック制御を P 制御 (proportional control; 比例制御) と呼ぶ。P 制御は単純な制御方式だが不安定な制御対象の外乱を抑止して安定させる効果がある。

入力がない状態で定常状態を保っている系に対しては正しく機能するが、時間的に変化しようとしている系に対しては正しい参照値に収束しない。
偏差 \(e(t)\) の時間積分を定数 \(K_i\) 倍した積分制御項を P 制御に加えたものを PI 制御 (P+integral control; 積分制御) と呼ぶ。
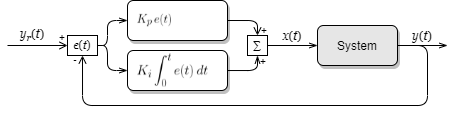
偏差 \(e(t)\) の時間微分を定数 \(K_d\) 倍した微分制御項を PI 制御に加えたものを PID 制御 (PI+derivative control; 微分制御) と呼ぶ。

P 制御が現在の偏差のみを考慮するのに対して、I 制御は過去の偏差の推移を考慮し、D 制御は将来の偏差の推移を考慮する。例えば自動車の速度制御が目標値を 60km/h としてた場合、PID それぞれの制御は 55km/h という現在の速度からアクセルの踏みの強さを以下のように考慮するかもしれない。

PID 制御は式 (\(\ref{pid}\)) のように表される。\[ \begin{eqnarray} e(t) & = & y_r(t) - y(t) \nonumber \\ x(t) & = & K_p e(t) + K_i \int_{\tau=0}^t e(\tau)\, d\tau + K_d \frac{d\, e(t)}{dt } \label{pid} \end{eqnarray} \]
 例: 自動車の速度制御
例: 自動車の速度制御
次のアプリケーションは PID 制御を使った簡易的なクルーズコントローラー (オートクルーズ) を実装している。正負の両方向に瞬時に無限の推進力が出せる理想の原動機を仮定して、空気抵抗、勾配抵抗、加速抵抗などの力が作用する状況で推進力 \(f_e\) を調整し目標の速度 \(v_\infty\) となるように制御している。
走行中に目標速度 \(v_\infty\) や勾配 \(\theta\) が変化しても目標速度で抵抗力と釣り合って収束することが分かるだろう。ただしバイアス \(K\) のとり方によっては正負の両方向に発散する。
\(K_i = K_d = 0\) と設定すると P 制御のみで速度を調整しようとする。ここで例えば勾配を 10% にすると目標の速度に到達する前に定常状態となることが分かるだろう。この現象は目標速度となるように調整された推進力が勾配抵抗によって消費されることによるもので、結果として P 制御のみでは目標より低い速度で力が釣り合ってしまうためである。このような偏差を定常偏差 (stationary error) と呼ぶ。定常偏差は I 制御を加えることによってなくすことができる。
