セキュリティ

電子署名

Takami Torao
  • このエントリーをはてなブックマークに追加

概要

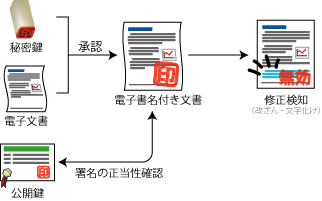
電子署名 (digital signature) は文書に対する承認と、文書内容の保障を電子的に付け加えるための暗号技術。公開鍵を使用することにより他人によって行われた署名でないことと、署名された時点から文書内容に変更がないことの 2 点を証明することができる。また電子署名法により 2001 年から電子商取引などにおける法的根拠としても利用可能となっている。

電子署名
Fig 1. 電子署名

電子署名を法的な保障付きで運用しようとすれば通常の公開鍵と同様のセキュリティが必要となる。秘密鍵は署名者本人以外からアクセス可能であってはならないし、公開鍵は信頼の置ける第三者機関から安全な方法で入手しなければならない。

公開鍵の有効期限が切れれば署名の正当性を証明する手段もなくなる。CA が発行する公開鍵の証明書には数年程度の有効期限しかないため、現実世界の契約書のような長期間の保管が必要な文書には向かない側面がある。

電子署名の原理

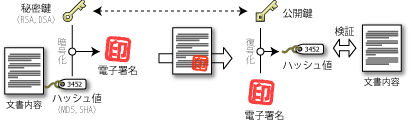
電子署名の実体は、文書から算出したハッシュ値を公開鍵暗号で暗号化した数百バイト程度のバイナリデータである。ただし、暗号化に秘密鍵を使用する点が文書秘匿を目的とした暗号と異なる。

電子署名
Fig 2. 電子署名と検証

署名の検証者は相手の公開鍵でその暗号が解除できるかどうかによって、対応する秘密鍵が使用された ─ つまりその所有者によって署名が行われたかどうかを検証することができる。そして署名から取り出したハッシュ値が文章のハッシュ値と一致していれば、その署名が行われてから文書に変更がないことを確定することができる。一般的に公開鍵暗号は非常に負荷の高い処理であるため、文書全体を暗号化する代わりに、それから算出した数十〜数百バイトのハッシュ値を使用する。

電子署名を信頼するには検証に使用する公開鍵が確実に相手のものであることを保証できなければならない。このため、一般的には CA によって身元が保証されている証明書に含まれている公開鍵が利用される。

アルゴリズム

RSA

因数分解問題の困難さを利用した公開鍵暗号アルゴリズム。公開鍵と秘密鍵の 2 つの鍵ペアを使用する。

  • メリット: 主要な OS やネットワークアプリケーションで利用できる。
  • デメリット: 基本的に処理速度が遅く、改ざん耐性のために暗号化強度を高くすると計算コストも膨大になる。最新のアルゴリズムと比較しての弱さから、サイドチャネル攻撃により秘密鍵を持たない第三者が署名から別の署名を作成できる可能性が指摘されている。

殆ど使われていないが、適応型選択暗号文攻撃 (CCA2) の耐性を高めた GMR 暗号署名、速度を改善した Rabin 暗号署名などいくつかの派生アルゴリズムが存在する。

DSA

DSA (Digital Signature Algorithm) は有限体で離散対数の計算困難性を利用した公開鍵暗号アルゴリズム。

  • メリット: 暗号化の強度が高い。一つの秘密鍵を使用して多数のメッセージの電子署名を生成できる。暗号化強度に拘らず署名の長さが短い。署名の処理速度が速い。
  • デメリット: 署名の検証には複雑な余剰計算が必要で遅い。

DSA の元となった ElGamal 署名には署名長が 2 倍になり計算速度の遅いなどの問題があった。DSA は現在でも署名アルゴリズムとして広く利用されているが、より高い強度を持ちサイズも小さい ECDSA への移行が進みつつある。

ECDSA

楕円曲線の点群における離散対数の計算困難性を利用した公開鍵暗号アルゴリズム。DSA アルゴリズムの修正バージョン。

  • メリット: 署名と検証の両面に置いて DSA よりはるかに計算が速く高い強度を持つ。
  • デメリット: 異なるデータに対して同一の値となる可能性が指摘されている (ただしそれには膨大な計算能力が必要)。

EdDSA

EdDSA (Edwards-curve Digital Signature Algorithm) は Twisted Edwards 曲線と Schnorr オプション基づく署名アルゴリズム。SHA-512/256 および Curve25519 に基づく署名スキーム Ed25519 が有名。

  • メリット: 高い強度を持ち高速。乱数ジェネレータが独立している。

DSA や ECDSA におけるセキュリティ問題を回避した上で優れたパフォーマンスを持っている。

電子署名の作成と検証

Java で利用できる電子署名アルゴリズムは Security.getAlgorithms("Signature") で取得することができる。詳細は Java:署名アルゴリズム参照。

scala> import java.security.Security
import java.security.Security

scala> Security.getAlgorithms("Signature")
res1: java.util.Set[String] = [SHA384WITHECDSA, SHA256WITHECDSAINP1363FORMAT, SHA224WITHDSAINP1363FORMAT, SHA512/224WITHRSA, SHA1WITHRSA, SHA512WITHRSA, SHA224WITHECDSAINP1363FORMAT, NONEWITHECDSAINP1363FORMAT, SHA384WITHECDSAINP1363FORMAT, SHA256WITHECDSA, SHA224WITHECDSA, SHA512/256WITHRSA, SHA512WITHECDSA, SHA1WITHDSA, NONEWITHDSA, SHA224WITHDSA, SHA256WITHRSA, SHA1WITHDSAINP1363FORMAT, MD5WITHRSA, SHA256WITHDSAINP1363FORMAT, SHA1WITHECDSAINP1363FORMAT, NONEWITHDSAINP1363FORMAT, MD2WITHRSA, SHA256WITHDSA, SHA1WITHECDSA, MD5ANDSHA1WITHRSA, SHA224WITHRSA, NONEWITHECDSA, RSASSA-PSS, SHA384WITHRSA, SHA512WITHECDSAINP1363FORMAT]

アルゴリズムを指定して秘密鍵で初期化した Signatureに対して、文書内容のバイナリデータで更新することで電子署名を算出することができる。生成される電子署名の実体は数百バイト程度のバイナリデータである。

Signature signature = Signature.getInstance("SHA256withRSA");
signature.initSign(privateKey);
signature.update(binary);
byte[] sign = signature.sign();

検証時は秘密鍵の代わりに公開鍵で初期化する。

Signature signature = Signature.getInstance("SHA256withRSA");
signature.initVerify(publicKey);
signature.update(binary);
boolean valid = signature.verify(sign);

これにより秘密鍵にアクセスできる人間しか署名を行うことができず、署名の検証は公開鍵を持つ誰でも行うことができる。