仕様翻訳: SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions - 転置に基づくハッシュ関数と拡張可能出力関数
 Abstract
Abstract
この標準はバイナリデータに対する Secure Hash Algorithm-3 (SHA-3) 関数ファミリーを規定する。各 SHA-3 関数は NIST が SHA-3 暗号化ハッシュアルゴリズム策定の勝者として選んだ Keccak-\(p\) アルゴリズムのインスタンスに基づいている。またこの標準は転置 (permutation) に基づく暗号関数の開発を促進するために Keccak の基礎となる転置を含む数学的転置の Keccak-\(p\) ファミリーも規定する。
SHA-3 ファミリーは SHA3-224, SHA3-256, SHA3-384 および SHA3-512 と呼ばれる 4 つの暗号論的ハッシュ関数と、SHAKE128 および SHAKE256 と呼ばれる 2 つの拡張可能出力関数 (XOF; extendable-output function) で構成されている。
ハッシュ関数は 1) デジタル署名の生成と検証、2) 鍵の導出、3) 疑似乱数ビットの生成など多くの重要な情報セキュリティアプリケーション構成要素である。この規格で規定されるハッシュ関数は SHA-1 ハッシュ関数と FIP 180-4 (Secure Hash Standard) で規定されている SHA-2 ハッシュ関数ファミリーを保管するものである。
拡張可能出力関数はハッシュ関数とは異なるが同様の方法で使用することができ、セキュリティを考慮した上で個々のアプリケーション要件に直接適合できる柔軟性を備えている。
キーワード: computer security, cryptography, extendable-output function, Federal Information Processing Standard, hash algorithm, hash function, information security, Keccak, message digest, permutation, SHA-3, sponge construction, sponge function, XOF.
Table of Contents
- Abstract
- 1 導入
- 2 用語集
- 3 Keccak-\(p\) 転置
- 4 スポンジ構造
- 5 Keccak
- 6 SHA-3 関数仕様
- 7 適合性
- A セキュリティ
- B 例
- C オブジェクト識別子
- D References
- 翻訳抄
 1 導入
1 導入
この標準は SHA-1 および FIPS 180-4 [1] で規定されているハッシュ関数ファミリーの SHA-2 を補完する新しい関数ファミリーを規定する。SHA-3 (Secure Hash Algorithm-3) と呼ばれるこのファミリーは Keccak ─ NIST が SHA-3 暗号ハッシュアルゴリズム策定 [3] の勝者として採択したアルゴリズム1に基づいている。SHA-3 ファミリーは 4 つの暗号論的ハッシュ関数と 2 つの拡張可能出力関数 (extandable-output function) で構成されている。これら 6 つの関数は [4] で説明されている構造、つまりスポンジ構造 (sponge construction) を共有しており、この構造を持つ関数をスポンジ関数と呼ぶ。
ハッシュ関数はバイナリデータ (つまりビット列) に対する関数で出力の長さが固定されている2。ハッシュ関数への入力はメッセージと呼ばれ、出力は (メッセージ) ダイジェストまたはハッシュ値と呼ばれる。ダイジェストは多くの場合、メッセージの要約表現として機能する。4 つの SHA-3 ハッシュ関数はそれぞれ SHA3-224, SHA3-256, SHA3-384, SHA3-512 という名前が付けられている。いずれの場合もダッシュ後の接尾辞はダイジェストの固定長を示し、例えば SHA3-256 は 256 ビットのダイジェストを生成する。SHA-2 関数、つまり SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224 および SHA-512/256 は同様のダイジェスト長のセットを提供する。したがって SHA-3 ハッシュ関数は SHA-2 関数の代替として実装することができ、またその逆も可能である。
拡張可能出力関数 (XOF; extendable-output function) はメッセージとも呼ばれるビット列に対する関数で出力を任意の長さに拡張することができる。2 つの SHA-3 XOF はそれぞれ SHAKE128 および SHAKE256 という名前が付けられている3。128 と 256 の接尾辞は、ハッシュ関数の接尾辞がダイジェスト長を表すのとは対照的に、これらの 2 つの関数が一般的4にサポートできるセキュリティ強度を示している。SHAKE128 と SHAKE256 は NIST が標準化した最初の XOF である。
6 つの SHA-3 関数は、衝突攻撃、原像攻撃、および第二原像攻撃に対する耐性などの特別な特性を提供するように設計されている。これら 3 種類の攻撃に対する耐性レベルはセクション A.1 にまとめされている。暗号論的ハッシュ関数は、電子署名の生成と検証、鍵の導出、疑似乱数ビットの生成など、様々な情報セキュリティアプリケーションにおける基本的な構成要素である。
FIPS が承認しているハッシュ関数のダイジェスト長は 160, 224, 256, 384, および 512 ビットである。アプリケーションが非標準のダイジェスト長を持つ暗号論的ハッシュ関数を必要とするのであれば、XOF はハッシュ関数を複数回呼び出したり出力ビットの切り捨てを行う構成に代わる自然な代替手段となる。しかし XOF はセクション A.2 で議論する追加のセキュリティ考慮事項が適用される。
6 つの SHA-3 関数のそれぞれはスポンジ構造の主要構成要素として同じ転置を採用している。事実上、SHA-3 関数は転置の動作モード (modes of operation) (modes) である。この標準では転置は Keccak-\(p\) と呼ばれる転置ファミリーのインスタンスとして規定されているが、これは将来の文書で追加モードを開発する際にそのサイズとセキュリティパラメータを変更できる柔軟性を提供するためである。
4 つの SHA-3 ハッシュ関数は SHA-3 策定 [3] で提案された Keccak のインスタンスとは若干異なる。特に SHA-3 ハッシュ関数と SHA-3 XOF を区別し、個々のアプリケーションドメインに特化した SHA-3 関数の新しいバリアントを開発することを容易にするためにメッセージに 2 ビットの接尾辞が付加されている。
また 2 つの SHA-3 XOF は専用のバリアント開発を可能にするように規定されている。さらに SHA-3 XOF は XOF の並列化可能なバリアント開発をサポートするために、別の文書で規定されているツリーハッシュ [7] に対する Sakura エンコーディングスキーム [6] と互換性がある。
この標準の表記と用語のほとんどは [8] の Keccak 仕様と一致している。
- 1より正確には策定では 4 つのハッシュ関数が求められたが Keccak はより大きな関数ファミリーである。
- 2多くのハッシュ関数には入力データの長さに (非常に大きな) 限度がある。
- 3"SHAKE" という名称は "Secure Hash Algorithm" with "KEccak" を組み合わせて [5] で提案された。
- 4例外は出力長が非常に小さい場合である。セクション A.1 の議論を参照。
 2 用語集
2 用語集
 2.1 用語と略語
2.1 用語と略語
| ビット (bit) | 2 進数: 0 または 1。この標準ではビットは Courier New フォントで示される。 |
| バイト (byte) | 8 ビットのシーケンス。 |
| 容量 (capacity) | スポンジ構造では、基礎となる関数の幅からレートを引いたもの。 |
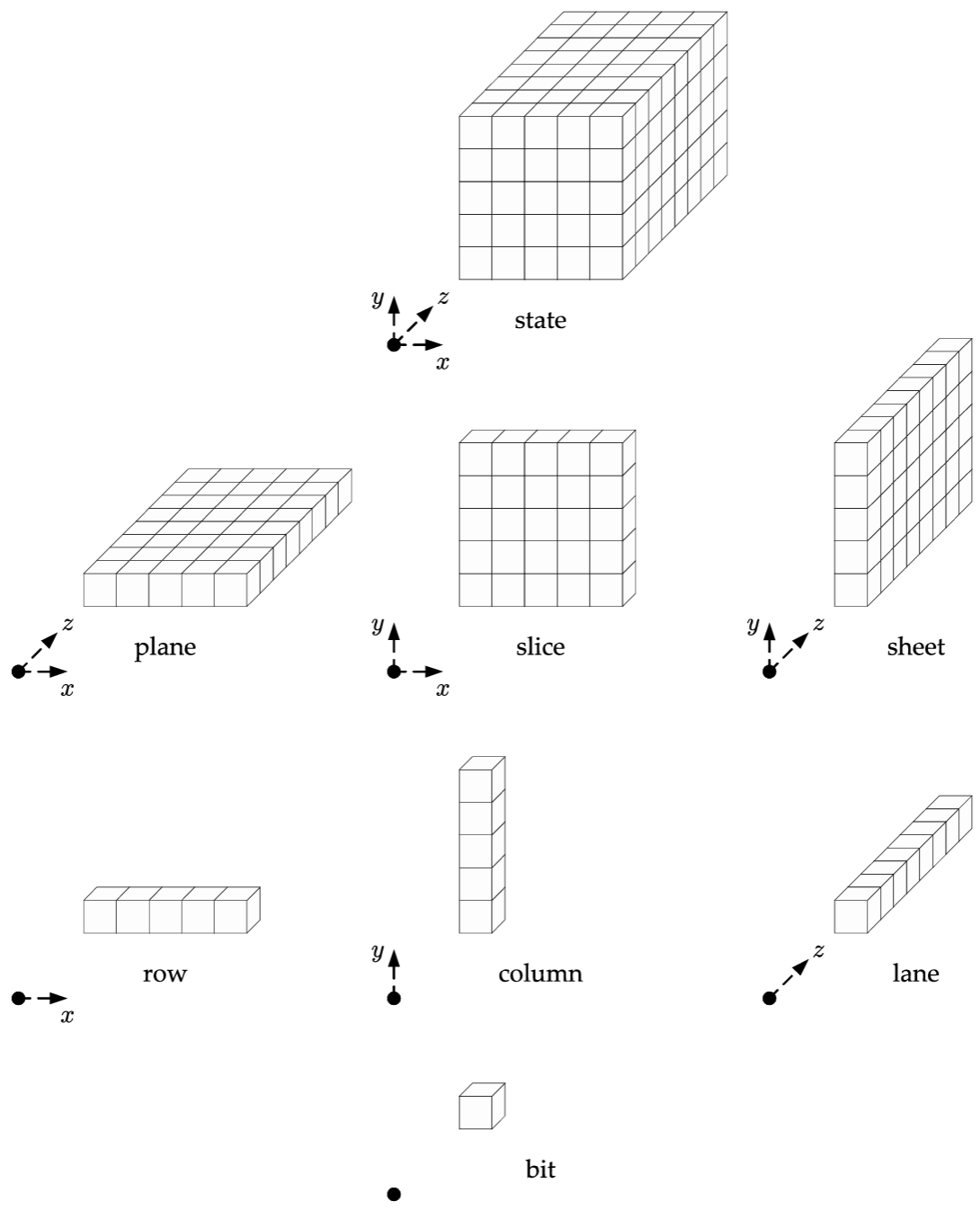
| 列 (column) | 状態配列に対して \(x\) および \(z\) 軸を持つ 5 ビットの部分配列。 |
| ダイジェスト (digest) | 暗号論的ハッシュ関数の出力。ハッシュ値とも呼ばれる。 |
| ドメイン分離 (domain separation) | 関数に対して、どの入力も単一のドメインに割り当てられるように異なるアプリケーションドメインへの入力を分離すること。 |
| 拡張可能出力関数 (XOF) (extendable-output function) | 出力を任意の希望する長さに拡張できるビット列の関数。 |
| FIPS | 連邦情報処理標準。 |
| FISMA | 連邦情報セキュリティ管理法。 |
| ハッシュ関数 | 出力の長さが肯定されているビット列関数。多くの場合、出力は入力の圧縮表現として機能する。 |
| ハッシュ関数 | ダイジェストを参照。 |
| HMAC | Keyed-Hash Message Authentication Code |
| KDF | 鍵導出関数。 |
| Keccak | Keccak-\(f\) 転置を基底関数とし、マルチレートパディングをパディングルールとするスポンジ関数のファミリー。Keccak はもともと [8] で規定された。 |
| レーン (lane) | 幅 \(b\) の Keccak-\(p\) 転置の状態配列に対して定数 \(x\) および \(y\) 座標を持つ \(b/25\) ビットの部分配列。 |
| メッセージ | SHA-3 関数への入力となる任意長のビット列。 |
| マルチレートパディング | パディングルール pad10*1。この出力はまず 1 がありその後に 0 個以上の 0 があり 1 で終わる。 |
| NIST | 米国国立標準技術研究所。 |
| プレーン (plane) | 幅 \(b\)の Keccak-\(p\) 転置の状態配列に対して定数 \(y\) 座標を持つ \(b/5\) ビットの部分配列。 |
| レート | スポンジ構造において、基礎となる関数を呼び出すごとによりされる入力ビットの威阿須、または生成される出力ビットの数。 |
| ラウンド | Keccak-\(p\) 転置の計算で反復されるステップマッピングのシーケンス。 |
| ラウンド定数 | Keccak-\(p\) 転置の各ラウンドに対して、ラウンドインデックスによって決定されるレーン値。ラウンド手数は \(\iota\) ステップマッピングの 2 番目の入力である。 |
| ラウンドインデックス | Keccak-\(p\) 転置のラウンドの整数インデックス値。 |
| 行 (row) | 状態配列に対して定数 \(y\) および \(z\) 座標の 5 ビットの部分配列。 |
| SHA-3 | Secure Hash Algorithm-3 |
| SHAKE | Secure Hash Algorithm Keccak |
| シート (sheet) | 幅 \(b\) の Keccak-\(p\) 転置の状態配列に対して定数 \(x\) を持つ \(b/5\) ビットの部分配列。 |
| スライス (slice) | 状態配列に対して定数 \(z\) 座標を持つ 25 ビットの部分配列。 |
| スポンジ構造 | 元は [4] で規定された、次のものから関数を定義する方法: 1) 固定長のビット列を基礎とする関数、2) パディングルール、3) レート。結果として得られる関数の入力はどちらも任意の長さのビット列である。 |
| スポンジ機能 | スポンジ構造に従って定義された関数。場合によっては固定出力長に特化している。 |
| 状態 | 計算手順の中で繰り返し更新されるビット配列。Keccak-\(p\) 転置の場合、状態は 3 次元配列またはビット列として表現される。 |
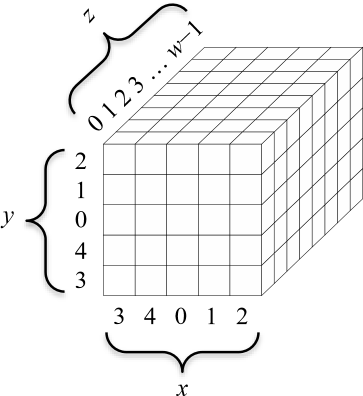
| 状態配列 | Keccak-\(p\) 転置に対して状態を表す \(5\times 5\times w\) の配列。\(x\), \(y\), \(z\) 座標の添え字はそれぞれ 0 から 4、0 から 4、0 から \(w-1\) の範囲である。 |
| ステップマッピング | Keccak-\(p\) 転置のラウンドの 5 つの構成要素の一つ: \(\theta\), \(\rho\), \(\pi\), \(\chi\), \(\iota\)。 |
| 列 (string) | 非負整数 \(m\) に対する \(m\) 個のシンボルのシーケンス。 |
| 幅 | スポンジ構造における基礎となる関数の入力と出力の固定長。 |
| XOF | 拡張出力関数を参照。 |
| XOR | 記号 \(\oplus\) で示されるブール排他論理和演算。 |
 2.2 アルゴリズムパラメータとその他の変数
2.2 アルゴリズムパラメータとその他の変数
| \(\vector{A}\) | 状態配列 |
| \(\vector{A}[x,y,z]\) | 状態配列 \(\vector{A}\) に対してタプル \((x,y,z)\) に対応するビット。 |
| \(b\) | Keccak-\(p\) 転置のビット幅。 |
| \(c\) | スポンジ関数の容量。 |
| \(d\) | ハッシュ関数のダイジェスト長、または XOF の出力に要求された長さ。単位はビット。 |
| \(f\) | スポンジ構造の一般的な基礎関数。 |
| \(i_r\) | Keccak-\(p\) 転置のラウンドインデックス。 |
| \(J\) | RawSHAKE128 または RawSHAKE256 への入力列。 |
| \(\ell\) | Keccak-\(p\) 転置に対するレーンサイズの 2 進対数、つまり \(\log_2(w)\)。 |
| \({\it Lane}(i,j)\) | 状態配列 \(\vector{A}\) に対して \(x\) と \(y\) 座標が \(i\) と \(j\) であるレーンのすべてのビット列。 |
| \(M\) | SHA-3 ハッシュまたは XOF 関数への入力列。 |
| \(N\) | \({\rm SPONGE}[f,{\rm pad},r]\) または Keccak\([c]\) への入力列。 |
| \(n_r\) | Keccak-\(p\) 転置に対するラウンド数。 |
| \({\rm pad}\) | スポンジ構造の一般的なパディングルール。 |
| \({\it Plane}(j)\) | 状態配列 \(\vector{A}\) に対して \(y\) 座標が \(j\) であるプレーンの全ビット列。 |
| \(r\) | スポンジ関数のレート。 |
| \(RC\) | Keccak-\(p\) 転置のラウンド定数。 |
| \(w\) | Keccak-\(p\) 転置のレーンビットサイズ、つまり \(b/25\)。 |
 2.3 基本操作と関数
2.3 基本操作と関数
| \({\tt 0}^s\) | 正の整数 \(s\) に対して \({\tt 0}^s\) は \(s\) 個の連続する \({\tt 0}\) からなる列。\(s=0\) であれば \({\tt 0}^s\) は空の列ある。 |
| \({\rm len}(X)\) | ビット列 \(X\) に対して \({\rm len}(X)\) は \(X\) のビット長である。 |
| \(X[i]\) | 列 \(X\) と \(0\ge i\lt {\rm len}(X)\) に対して \(X[i]\) はインデックス \(i\) となる \(X\) のビットである。ビット列は左から右に増加するインデックスで表され、\(X[0]\) が左にあり \(X[1]\) がそれに続く。例えば \(X={\tt 101000}\) であれば \(X[2]=1\) である。 |
| \({\rm Trunc}_s(X)\) | 正の整数 \(s\) と列 \(X\) に対して \({\rm Trunc}_s(X)\) はビット \(X[0]\) から \(X[s-1]\) で構成される列である。例えば \({\rm Trunc}2({\tt 10100})={\tt 10}\) である。 |
| \(X\oplus Y\) | ビット長が等しい列 \(X\) と \(Y\) に対する \(X\oplus Y\) は各ビット位置で \(X\) と \(Y\) にブール排他的論理和を適用した結果の列である。例えば \({\tt 1100}\oplus{\tt 1010}={\tt 0110}\) となる。 |
| \(X||Y\) | 列 \(X\) と \(Y\) に対する \(X||Y\) は \(X\) と \(Y\) を連結する。例えば \({\tt 11001}||{\tt 010}={\tt 11001010}\) となる。 |
| \(m/n\) | 整数 \(m\) および \(n\) に対する \(m/n\) は商、つまり \(m\) を \(n\) で割ったものである。 |
| \(m \bmod n\) | 整数 \(m\) および \(n\) に対する \(m \bmod n\) は、\(0\le r\lt n\) であり \(m-r\) が \(n\) の倍数となる整数 \(r\) である。例えば \(11 \bmod 5 = 1\) であり \(-11 \bmod 5 = 4\) である。 |
| \(\lceil x\rceil\) | 実数 \(x\) に対する \(\lceil x\rceil\) は厳密に \(x\) より小さくない最小の整数である。例えば \(\lceil 3.2\rceil=4\), \(\lceil -3.2\rceil=-3\), \(\lceil 6\rceil=6\) となる。 |
| \(\log_2(x)\) | 正の実数 \(x\) に対する \(\log_2(x)\) は \(2^y=x\) となる実数 \(y\) である。 |
| \(\min(x,y)\) | 実数 \(x\) と \(y\) に対する \(\min(x,y)\) は \(x\) と \(y\) の最小値である。例えば \(\min(9,33)=9\) となる。 |
 2.4 特定の機能
2.4 特定の機能
| \(\theta\), \(\rho\), \(\pi\), \(\chi\), \(\iota\) | ラウンドを構成する 5 つのステップのマッピング。 |
| Keccak\([c]\) | Keccak-\(f[1600]\) を起訴とする転置と容量 \(c\) の Keccak インスタンス。 |
| Keccak-\(f[b]\) | Keccak の基礎関数として [8] で規定された 7 つの転置のファミリー。転置の幅 \(b\) の集合は {25,50,100,200,400,800,1600} である。 |
| Keccak-\(p[b,n_r]\) | Keccak-\(p[b]\) 転置の一般化であり、ラウンド数 \(n_r\) を入力パラメータに変換することでこの標準で定義されている。 |
| pad10*1 | 元は [8] で規定された Keccak のマルチレートパディングルール。 |
| RawSHAKE128 | SHAKE128 の代替定義の中間関数。 |
| RawSHAKE256 | SHAKE256 の代替定義の中間関数。 |
| \(rc\) | ラウンド定数の可変ビットを生成する関数。 |
| Rnd | Keccak 転置のラウンド関数。 |
| SHA3-224 | 224 ビットのダイジェストを生成する SHA-3 ハッシュ関数。 |
| SHA3-256 | 256 ビットのダイジェストを生成する SHA-3 ハッシュ関数。 |
| SHA3-384 | 384 ビットのダイジェストを生成する SHA-3 ハッシュ関数。 |
| SHA3-512 | 512 ビットのダイジェストを生成する SHA-3 ハッシュ関数。 |
| SHAKE128 | 出力が十分に長い場合、通常 128 ビットのセキュリティ強度をサポートする SHA-3 XOF。セクション A.1 参照。 |
| SHAKE256 | 出力が十分に長い場合、通常 256 ビットのセキュリティ強度をサポートする SHA-3 XOF。セクション A.1 参照。 |
| SPONGE\([f,{\rm pad},r]\) | 基礎関数 \(f\)、パディングルール pad、およびレート \(r\) を持つスポンジ関数。 |
 3 Keccak-\(p\) 転置
3 Keccak-\(p\) 転置
このセクションでは Keccak-\(p\) 転置を 2 つのパラメータで規定する: 1) 転置の幅と呼ばれる並べ換えられる列の固定長、および 2) ラウンドと呼ばれる内部変換の反復回数。幅は \(b\) で表され、ラウンド数は \(n_r\) で表される。ラウンド \(n_r\) と幅 \(b\) を持つ Keccak-\(p\) 転置は Keccak-\(p[b,n_r]\) と表される。この並べ替えは {25,50,100,200,400,800,1600} のいずれかの \(b\) と、任意の正の整数 \(n_r\) に対して定義される。
Keccak-\(p\) 転置の 1 ラウンドは Rnd と表記され、ステップマッピングと呼ばれる 5 つの変換のシーケンスで構成される。転置は状態と呼ばれる繰り返し更新される \(b\) ビット値の配列で規定される。初期の状態は転置の入力値に設定される。状態の表記と用語についてはセクション 3.1 で説明する。ステップマッピングはセクション 3.2 で規定する。ラウンド関数 Rnd を含む Keccak-\(p\) 転置はセクション 3.3 で規定する。[8] で Keccak に対して定義された Keccak-\(f\) はセクション 3.4 で説明する。
 3.1 状態
3.1 状態
Keccak-\(p[b,n_r]\) 転置の状態は \(b\) ビットで構成される。この標準での仕様は \(b\) に関連する他の 2 つの量、\(b/25\) および \(\log_2(b/25)\) が含まれており、それぞれ \(w\) と \(\ell\) で表記される。Keccak-\(p\) 転置で定義されるこれらの変数が取り得る 7 つの値は以下の Table 1 の列で示される。
| \(b\) | 25 | 50 | 100 | 200 | 400 | 800 | 1600 |
|---|---|---|---|---|---|---|---|
| \(w\) | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
| \(\ell\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
転置の入力と出力の状態を \(b\) ビット列で表し、ステップマッピングの入力と出力状態を \(5\times 5\times w\) ビット配列で表すと便利である。状態を表す列を \(S\) と表記するとそのビットは 0 から \(b-1\) までのインデックスを持つ。\[ S = S[0] \ ||\ S[1] \ ||\ \ldots \ ||\ S[b-2] \ ||\ S[b-1] \] 状態を表す \(5\times 5\times w\) ビット配列を \(\vector{A}\) と表記すると、そのインデックスは \(0\le x\lt 5\), \(0\le y\lt 5\), \(0\le z\lt w\) となるタプル \((x,y,z)\) である。\((x,y,z)\) に対応するビットは \(\vector{A}[x,y,z]\) と表記される。状態配列はこの方法でインデックスが付けた 3 次元配列で状態を表現したものである。
 3.1.1 状態配列の部分
3.1.1 状態配列の部分
Keccak-\(p\) 転置の状態配列とその低次元部分配列は上記 Figure 1 に示すように \(b=200\)、つまり \(w=8\) と示される。2 次元の部分配列はシート、プレーン、およびスライスと呼ばれ、1 次元の部分配列は行、列、およびレーンと呼ばれる。これらの部分配列の代数的定義はセクション 2.1 の用語集にある。
 3.1.2 列から状態配列への変換
3.1.2 列から状態配列への変換
Keccak-\(p[b,n_r]\) 転置の状態を表す \(b\) ビット列を \(S\) とする。それに対応する、\(\vector{A}\) と表記される状態配列は次のように定義される:
\(0\le x\lt 5\), \(0\le y\lt 5\), \(0\le z\lt w\) となるすべてのタプル \((x,y,z)\) に対して \[ \vector{A}[x,y,z] = S[w(5y+x)+z] \] である。例えば \(b=1600\) では \(w=64\) であるため \[ \begin{array}{llcl} \vector{A}[0,0,0]=S[0] & \vector{A}[1,0,0]=S[64] & & \vector{A}[4,0,0]=S[256] \\ \vector{A}[0,0,1]=S[1] & \vector{A}[1,0,0]=S[65] & & \vector{A}[4,0,0]=S[257] \\ \vector{A}[0,0,2]=S[2] & \vector{A}[1,0,0]=S[66] & & \vector{A}[4,0,0]=S[258] \\ \vdots & \vdots & \cdots & \vdots \\ \vector{A}[0,0,61]=S[61] & \vector{A}[1,0,61]=S[125] & & \vector{A}[4,0,61]=S[317] \\ \vector{A}[0,0,62]=S[62] & \vector{A}[1,0,62]=S[126] & & \vector{A}[4,0,62]=S[318] \\ \vector{A}[0,0,63]=S[63] & \vector{A}[1,0,63]=S[127] & & \vector{A}[4,0,63]=S[319] \\ \end{array} \] そして \[ \begin{array}{llcl} \vector{A}[0,1,0]=S[320] & \vector{A}[1,1,0]=S[384] & & \vector{A}[4,1,0]=S[576] \\ \vector{A}[0,1,1]=S[321] & \vector{A}[1,1,0]=S[385] & & \vector{A}[4,1,0]=S[577] \\ \vector{A}[0,1,2]=S[322] & \vector{A}[1,1,0]=S[386] & & \vector{A}[4,1,0]=S[578] \\ \vdots & \vdots & \cdots & \vdots \\ \vector{A}[0,1,61]=S[381] & \vector{A}[1,1,61]=S[445] & & \vector{A}[4,1,61]=S[637] \\ \vector{A}[0,1,62]=S[382] & \vector{A}[1,1,62]=S[446] & & \vector{A}[4,1,62]=S[638] \\ \vector{A}[0,1,63]=S[383] & \vector{A}[1,1,63]=S[447] & & \vector{A}[4,1,63]=S[639] \\ \end{array} \] そして \[ \begin{array}{llcl} \vector{A}[0,2,0]=S[640] & \vector{A}[1,2,0]=S[704] & & \vector{A}[4,2,0]=S[896] \\ \vector{A}[0,2,1]=S[641] & \vector{A}[1,2,0]=S[705] & & \vector{A}[4,2,0]=S[897] \\ \vector{A}[0,2,2]=S[642] & \vector{A}[1,2,0]=S[706] & & \vector{A}[4,2,0]=S[898] \\ \vdots & \vdots & \cdots & \vdots \\ \vector{A}[0,2,61]=S[701] & \vector{A}[1,2,61]=S[765] & & \vector{A}[4,2,61]=S[957] \\ \vector{A}[0,2,62]=S[702] & \vector{A}[1,2,62]=S[766] & & \vector{A}[4,2,62]=S[958] \\ \vector{A}[0,2,63]=S[703] & \vector{A}[1,2,63]=S[767] & & \vector{A}[4,2,63]=S[959] \\ \end{array} \] などとなる。
 3.1.3 状態変数から列への変換
3.1.3 状態変数から列への変換
\(\vector{A}\) を状態配列とする。それに対応する \(S\) と表記する列表現は \(\vector{A}\) のレーンとプレーンから次のように構築できる:
\(0\le i\lt 5\), \(0\le j\lt 5\) となるような整数ペア \((i,j)\) それぞれに対して列 \(Lane(i,j)\) は \[ Lane(i,j) = \vector{A}[i,j,0] \ || \vector{A}[i,j,1] \ || \ldots \ || \vector{A}[i,j,w-2] \ || \ \vector{A}[i,j,w-1] \] と定義される。例えば \(b=1600\) では \(w=64\) であるため \[ \begin{array}{l} Lane(0,0) = \vector{A}[0,0,0] \ || \ \vector{A}[0,0,1] \ || \ \vector{A}[0,0,2] \ || \ \ldots \ || \vector{A}[0,0,62] \ || \ \vector{A}[0,0,63] \\ Lane(1,0) = \vector{A}[1,0,0] \ || \ \vector{A}[1,0,1] \ || \ \vector{A}[1,0,2] \ || \ \ldots \ || \vector{A}[1,0,62] \ || \ \vector{A}[1,0,63] \\ Lane(2,0) = \vector{A}[2,0,0] \ || \ \vector{A}[2,0,1] \ || \ \vector{A}[2,0,2] \ || \ \ldots \ || \vector{A}[2,0,62] \ || \ \vector{A}[2,0,63] \\ \end{array} \] などとなる。
\(0\le j\lt 5\) となるような整数 \(j\) に対して、列 \(Plane(j)\) は \[ Plane(j) = Lane(0,j) \ || \ Lane(1,j) \ || \ \ldots \ || \ Lane(4,j) \] と定義される。ここで \[ S = Plane(0) \ || \ Plane(1) \ || \ \ldots \ || \ Plane(4) \] である。例えば \(b=1600\) では \(w=64\) であるため \[ \begin{eqnarray*} S & = & \ \ \ \vector{A}[0,0,0] \ || \ \vector{A}[0,0,1] \ || \ \vector{A}[0,0,2] \ || \ \ldots \ || \vector{A}[0,0,62] \ || \ \vector{A}[0,0,63] \\ && || \ \vector{A}[1,0,0] \ || \ \vector{A}[1,0,1] \ || \ \vector{A}[1,0,2] \ || \ \ldots \ || \vector{A}[1,0,62] \ || \ \vector{A}[1,0,63] \\ && || \ \vector{A}[2,0,0] \ || \ \vector{A}[2,0,1] \ || \ \vector{A}[2,0,2] \ || \ \ldots \ || \vector{A}[2,0,62] \ || \ \vector{A}[2,0,63] \\ && || \ \vector{A}[3,0,0] \ || \ \vector{A}[3,0,1] \ || \ \vector{A}[3,0,2] \ || \ \ldots \ || \vector{A}[3,0,62] \ || \ \vector{A}[3,0,63] \\ && || \ \vector{A}[4,0,0] \ || \ \vector{A}[4,0,1] \ || \ \vector{A}[4,0,2] \ || \ \ldots \ || \vector{A}[4,0,62] \ || \ \vector{A}[4,0,63] \\ \\ && || \ \vector{A}[0,1,0] \ || \ \vector{A}[0,1,1] \ || \ \vector{A}[0,1,2] \ || \ \ldots \ || \vector{A}[0,1,62] \ || \ \vector{A}[0,1,63] \\ && || \ \vector{A}[1,1,0] \ || \ \vector{A}[1,1,1] \ || \ \vector{A}[1,1,2] \ || \ \ldots \ || \vector{A}[1,1,62] \ || \ \vector{A}[1,1,63] \\ && || \ \vector{A}[2,1,0] \ || \ \vector{A}[2,1,1] \ || \ \vector{A}[2,1,2] \ || \ \ldots \ || \vector{A}[2,1,62] \ || \ \vector{A}[2,1,63] \\ && || \ \vector{A}[3,1,0] \ || \ \vector{A}[3,1,1] \ || \ \vector{A}[3,1,2] \ || \ \ldots \ || \vector{A}[3,1,62] \ || \ \vector{A}[3,1,63] \\ && || \ \vector{A}[4,1,0] \ || \ \vector{A}[4,1,1] \ || \ \vector{A}[4,1,2] \ || \ \ldots \ || \vector{A}[4,1,62] \ || \ \vector{A}[4,1,63] \\ \\ && \vdots \\ \\ && || \ \vector{A}[0,4,0] \ || \ \vector{A}[0,4,1] \ || \ \vector{A}[0,4,2] \ || \ \ldots \ || \vector{A}[0,4,62] \ || \ \vector{A}[0,4,63] \\ && || \ \vector{A}[1,4,0] \ || \ \vector{A}[1,4,1] \ || \ \vector{A}[1,4,2] \ || \ \ldots \ || \vector{A}[1,4,62] \ || \ \vector{A}[1,4,63] \\ && || \ \vector{A}[2,4,0] \ || \ \vector{A}[2,4,1] \ || \ \vector{A}[2,4,2] \ || \ \ldots \ || \vector{A}[2,4,62] \ || \ \vector{A}[2,4,63] \\ && || \ \vector{A}[3,4,0] \ || \ \vector{A}[3,4,1] \ || \ \vector{A}[3,4,2] \ || \ \ldots \ || \vector{A}[3,4,62] \ || \ \vector{A}[3,4,63] \\ && || \ \vector{A}[4,4,0] \ || \ \vector{A}[4,4,1] \ || \ \vector{A}[4,4,2] \ || \ \ldots \ || \vector{A}[4,4,62] \ || \ \vector{A}[4,4,63] \\ \end{eqnarray*} \]
 3.1.4 状態配列のラベル付け規則
3.1.4 状態配列のラベル付け規則
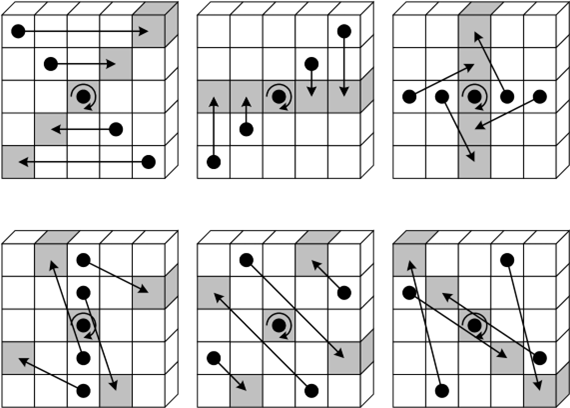
ステップマッピングの仕様に付随する状態の図では、座標 \((x,y)=(0,0)\) に対するレーンはスライスの中央に描かれている。これらの図の \(x\), \(y\), および \(z\) 座標の完全なレベル付けを上記 Figure 2 に示す。
 3.2 ステップマッピング
3.2 ステップマッピング
Keccak-\(p[b,n_r]\) のラウンドを構成する 5 つのステップマッピングは \(\theta\), \(\rho\), \(\pi\), \(\chi\), および \(\iota\) とする。これらの関数の仕様はセクション 3.2.1-3.2.5 で示す。
各ステップマッピングのアルゴリズムは \(\vector{A}\) で示される状態配列を入力として受け取り、\(\vector{A}'\) で示される更新された状態配列を出力として返す。状態のサイズはステップマッピングが呼び出されるときに常に \(b\) が指定されるため表記からは省略されるパラメータである。
\(\iota\) マッピング \(i_r\) には第 2 の入力、すなわち \(i_r\) で示されるラウンドインデックスと呼ばれる整数がある。これはセクション 3.3 で Keccak-\(p[b,n_r]\) に対するアルゴリズム 7 で定義される。その他のステップマッピングはラウンドインデックスには依存しない。
 3.2.1 \(\theta\) の仕様
3.2.1 \(\theta\) の仕様
アルゴリズム 1: \(\theta(\vector{A})\)
入力: 状態配列 \(\vector{A}\)
出力: 状態配列 \(\vector{A}'\)
ステップ:
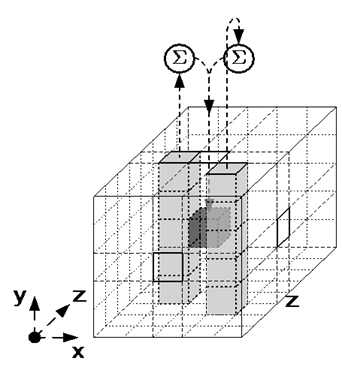
\(0\le x\lt 5\) および \(0\le z\lt w\) となるすべてのペア \((x,z)\) に対して \[ C[x,z] = \vector{A}[x,0,z] \oplus \vector{A}[x,1,z] \oplus \vector{A}[x,2,z] \oplus \vector{A}[x,3,z] \oplus \vector{A}[x,4,z] \] とする。
\(0\le x\lt 5\) および \(0\le z\lt w\) となるすべてのペア \((x,z)\) に対して \[ D[x,z] = C[(x-1)\bmod 5,z] \oplus C[(x+1)\bmod 5,(z-1)\bmod w] \] とする。
\(0\le x\lt 5\)、\(0\le y\lt 5\)、および \(0\le z\lt w\) となるすべてのトリプル \((x,y,z)\) に対して \[ \vector{A}'[x,y,z] = \vector{A}[x,y,z] \oplus D[x,z] \] とする。
\(\theta\) の効果は状態の各ビットと配列の 2 つの列のパリティを XOR することである。特にビット \(\vector{A}[x_0,y_0,z_0]\) の場合、列の一つの \(x\) 座標は \((x_0+1) \bmod 5\)、同じ \(z\) 座標 \(z_0\) で、他の列の \(x\) 座標は \((x_0+1) \bmod 5\)、\(z\) 座標は \((z_0-1) \bmod w\) である。
以下に示す Figure 3 の \(\theta\) ステップマッピングの図では、合計記号 \(\sum\) はパリティ、すなはち列内の全ビットの XOR 合計を示す。
 3.2.2 \(\rho\) の仕様
3.2.2 \(\rho\) の仕様
アルゴリズム 2: \(\rho(\vector{A})\)
入力: 状態配列 \(\vector{A}\)
出力: 状態配列 \(\vector{A}'\)
ステップ:
\(0\le z\lt w\) となるすべての \(z\) に対して、\(\vector{A}'[0,0,z] = \vector{A}[0,0,z]\) とする。
\((x,y)=(1,0)\) とする。
0 から 23 の \(t\) に対して
\(0\le z\lt w\) となるすべての \(z\) に対して、\(\vector{A}'[x,y,z] = \vector{A}[x,y,(z-(t+1)(t+2)/2) \bmod w]\) とする。
\((x,y)=(y,(2x+3y) \bmod 5)\) とする。
\(\vector{A}'\) を返す。
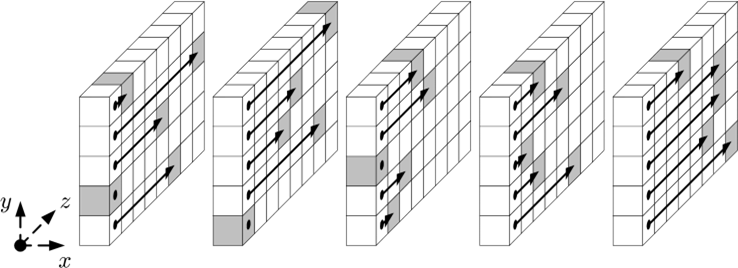
\(\rho\) の効果は各レーンのビットをオフセットと呼ばれる長さだけ循環させることである。オフセットはレーンの固定 \(x\) 座標と \(y\) 座標に依存する。同様に、レーン内の各ビットに対して、レーンサイズを法とするオフセットを加算することによって \(z\) 座標が変更される。
| \(x=3\) | \(x=4\) | \(x=0\) | \(x=1\) | \(x=2\) | |
|---|---|---|---|---|---|
| \(y=2\) | 153 | 231 | 3 | 10 | 171 |
| \(y=1\) | 55 | 276 | 36 | 300 | 6 |
| \(y=0\) | 28 | 91 | 0 | 1 | 190 |
| \(y=4\) | 120 | 78 | 210 | 66 | 253 |
| \(y=3\) | 21 | 136 | 105 | 45 | 15 |
アルゴリズム 2 のステップ 3.1 の計算結果から得られた各レーンのオフセットを上記 Table 2 に示す。
\(w=8\) の場合の \(\rho\) を Figure 4 に示す。Figure 4 の \(x\) と \(y\) 座標に対するラベル付け規則は Table 2 の行と列に対応しており、Figure 2 に明示されている。例えばレーン \(\vector{A}[0,0]\) は中央のシートの真ん中に描かれており、レーン \(\vector{A}[2,3]\) は一番右のシートの下部に描かれている。
Figure 4 の各レーンについて、黒い点は \(z\) 座標が 0 のビットを表しており、薄暗い立方体は \(\rho\) 実行後のそのビットの位置を示している。レーンの他のビットは同じオフセットだけシフトし、そのシフトは循環的である。例えば、レーン \(\vector{A}[1,0]\) のオフセットは 1 であるため、この例では \(z\) 座標が 7 となる最後のビットが、\(z\) 座標が 0 となる前方の位置にシフトする。その結果、オフセットはレーンサイズを法として減少する可能性がある。例えば最左シートの一番上に位置するレーン \(\vector{A}[3,2]\) のオフセットはこの例では \(153 \bmod 8\) であり、すなはちオフセットは 1 ビットである。
 3.2.3 \(\pi\) の仕様
3.2.3 \(\pi\) の仕様
アルゴリズム 3: \(\pi(\vector{A})\)
入力: 状態配列 \(\vector{A}\)
出力: 状態配列 \(\vector{A}'\)
ステップ:
\(0 \le x \lt 5\), \(0 \le y \lt 5\), \(0 \le z \lt w\) となるすべてのトリプル \((x,y,z)\) に対して \[\vector{A}'[x,y,z] = \vector{A}[(x+3y) \bmod 5, x, z]\] とする。
\(\vector{A}'\) を返す。
\(\pi\) の効果は以下の図 Figure 5 のスライスで示されているよう、レーンの位置を再配置することである。座標のラベル付けの規則は前述 Figure 2 に示されている。例えば座標 \(x=y=0\) のビットはスライスの中央に描かれている。
 3.2.4 \(\chi\) の仕様
3.2.4 \(\chi\) の仕様
アルゴリズム 4: \(\chi(\vector{A})\)
入力: 状態配列 \(\vector{A}\)
出力: 状態配列 \(\vector{A}'\)
ステップ:
\(0 \le x \lt 5\), \(0 \le y \lt 5\), \(0 \le z \lt w\) となるすべてのトリプル \((x,y,z)\) に対して \[\vector{A}'[x,y,z] = \vector{A}[x,y,z] \oplus ((\vector{A}[(x+1) \bmod 5, y, z] \oplus 1) \cdot \vector{A}[(x+2) \bmod 5, y, z])\] とする。
\(\vector{A}'\) を返す。
ステップ 1 の代入の右側のドットは整数の乗算を表し、この場合は、これは意図されたブール "AND" 演算に相当する。
\(\chi\) の効果は以下の図 Figure 6 に示されるように各ビットをその行内の他の 2 つのビットの非線形関数で XOR することである。
 3.2.5 \(\iota\) の仕様
3.2.5 \(\iota\) の仕様
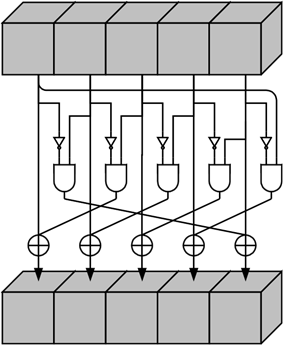
\(\iota\) マッピングはラウンドインデックス \(i_r\) でパラメータ化され、その値はセクション 3.3 において Keccak-\(p[b,n_r]\) を算出するための Algorithm 7 のステップ 2 で規定される。以下の Algorithm 6 の \(\iota\) の仕様内で、このパラメータは \(RC\) と示されるラウンド定数と呼ばれるレーン値の \(\ell+1\) ビットを決定する。これらの \(\ell+1\) ビットはそれぞれ線形フィードバックシフトレジスタに基づく関数によって生成される。\(rc\) で示されるこの関数は Algorithm 5 で規定される。
アルゴリズム 5: \(rc(t)\)
入力: 整数 \(t\)
出力: ビット \(rc(t)\)
ステップ:
もし \(t \bmod 255 = 0\) であれば 1 を返す。
\(R={\tt 10000000}\) とする。
1 から \(t \bmod 255\) までの \(i\) に対して
- \(R=0\,||\,R;\)
- \(R[0] = R[0] \oplus R[8];\)
- \(R[4] = R[4] \oplus R[8];\)
- \(R[5] = R[5] \oplus R[8];\)
- \(R[6] = R[6] \oplus R[8];\)
- \(R={\rm Trunc}_8[R]\)
とする。
\(R[0]\) を返す。
アルゴリズム 6: \(\iota(\vector{A},i_r)\)
入力: 状態配列 \(\vector{A}\); ラウンドインデックス \(i_r\)
出力: 状態配列 \(\vector{A}'\)
ステップ:
\(0\le x\lt 5\), \(0\le y\lt 5\) および \(0\le z\lt w\) となるすべてのトリプル \((x,y,z)\) に対して \(\vector{A}'[x,y,z]=\vector{A}[x,y,z]\) とする。
\(RC={\tt 0}^w\) とする。
0 から \(\ell\) までの \(j\) に対して \(RC[2^j-1] = rc(j+7i_r)\) とする。
\(0\le z\lt w\) となるすべての \(z\) に対して \(\vector{A}'[0,0,z]=\vector{A}[0,0,z] \oplus RC[z]\) とする。
\(\vector{A}'\) を返す。
\(\iota\) の効果は、ラウンドインデックス \(i_r\) に依存する方法で \({\rm Lane}(0,0)\) のビットの一部を変更することである。その他の 24 のレーンは \(\iota\) の影響を受けない。
 3.3 Keccak-\(p[b,n_r]\)
3.3 Keccak-\(p[b,n_r]\)
状態配列 \(\vector{A}\) とラウンドインデックス \(i_r\) が与えられると、ラウンド関数 \({\rm Rnd}\) はステップマッピング \(\theta\), \(\rho\), \(\pi\), \(\chi\), \(\pi\), \(\iota\) をこの順序で適用した結果として得られる変換である。つまり: \[ {\rm Rnd}(\vector{A},i_r)=\iota(\chi(\pi(\rho(\theta(\vector{A})))),i_r) \] Keccak-\(p[b,n_r]\) 転置は Algorithm 7 で規定されるように \({\rm Rnd}\) の \(n_r\) 回の繰り返しで構成されている。
アルゴリズム 7: Keccak-\(p[b,n_r](S)\)
入力: 長さ \(b\) の列 \(S\); ラウンド数 \(n_r\)
出力: 長さ \(b\) の列 \(S'\)
ステップ:
セクション 3.1.2 で説明したように \(S\) を状態配列 \(\vector{A}\) に変換する。
\(12+2\ell-n_r\) から \(12+2\ell-1\) までの \(i_r\) に対して \(\vector{A}={\rm Rnd}(\vector{A},i_r)\) とする。
\(\vector{A}\) をセクション 3.1.3 で説明したように長さ \(b\) の列 \(S'\) に変換する。
\(\vector{A}'\) を返す。
 3.4 Keccak-\(f\) との比較
3.4 Keccak-\(f\) との比較
転置の Keccak-\(f\) ファミリーは元々 [8] で定義されたもので、\(n_r=12+2\ell\) ケースに特化した Keccak-\(p\) ファミリーである: \[ {\rm K{\scriptsize ECCAK}}\mbox{-}f[b] = {\rm K{\scriptsize ECCAK}}\mbox{-}p[b,12+2\ell] \] したがって 6 個の SHA-3 関数の基礎となる Keccak-\(p[1600,24]\) 転置は Keccak-\(f[1600]\) と等価である。
Keccak-\(f[b]\) のラウンドは 0 から \(11+2\ell\) までのインデックスが付けられる。 Algorithm 7 のステップ 2 におけるインデックス付けの結果、Keccak-\(p[b,n_r]\) のラウンドは Keccak-\(f[b]\) のラウンドと一致し、またその逆もしかりである。例えば Keccak-\(p[1600,19]\) は Keccak-\(f[1600]\) の最後の 19 ラウンドと等価であるし、同様に Keccak-\(f[1600]\) は Keccak-\(p[1600,30]\) の最後の 24 ラウンドと等価である; この場合、Keccak-\(p[1600,30]\) の先行するラウンドは -6 から -1 までの整数でインデックス付けされる。
 4 スポンジ構造
4 スポンジ構造
スポンジ構造 (sponge construction) [4] は任意の出力長を持つバイナリデータに対する関数を規定するためのフレームワークである。この構造には次の 3 つのコンポーネントが使用される:
- \(f\) で表される、固定長の列の基礎となる関数、
- \(r\) で表される、レートと呼ばれるパラメータ、および
- pad で表されるパディングルール。
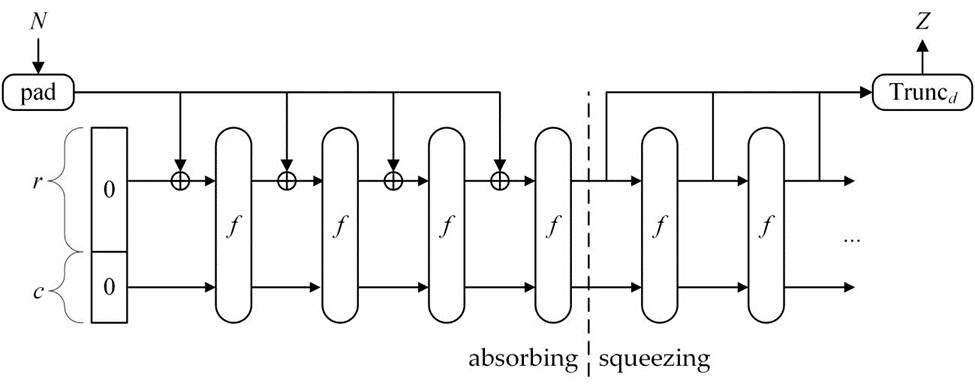
これらのコンポーネントから構造が生成する関数はスポンジ関数と呼ばれ SPONGE\([f,{\rm pad},r]\) で表される。スポンジ関数は \(N\) で示されるビット列と \(d\) で示される出力ビット長、SPONGE\([f,{\rm pad},r](N,d)\) の 2 つの入力を取る。スポンジとの類似性は、任意数の入力ビットが関数の状態に "吸収" され、その後にその状態から任意数の出力ビットが "絞り出される" という点にある。
スポンジ構造は [4] から引用した以下の Figure 7 に示される。
関数 \(f\) は、\(b\) で示される単一の固定長列を同じ長さの列にマップする。セクション 3 のように \(b\) は \(f\) の幅と呼ばれる。セクション 6 で規定される SHA-3 関数は、関数 \(f\) が可逆、すはなち転置であるスポンジ構造のインスタンスだが、スポンジ構造では \(f\) が可逆である必要はない。
レート \(r\) はビット幅 \(b\) より厳密に小さい正の整数である。\(c\) で示される容量は正の整数 \(b-r\) である。したがって \(r+c=b\) となる。
パディングルール \({\rm pad}\) はパディング、つまりある列に追加する適切な長さの列を生成する関数である。一般に、正の整数 \(x\) と非負整数 \(m\) を指定すると、出力 \({\rm pad}(x,m)\) は \(m+{\rm len}(N)\) が \(x\) の正の倍数という特性を持つ列となる。スポンジ構造内では \(x=r\) と \(m={\rm len}(N)\) であり、パディングされた入力列は \(r\) ビット列のシーケンスに分割できる。セクション 5.1 の Algorithm 9 は Keccak 関数、つまり SHA-3 関数のパディングルールを規定する。
以上のように \(f\), \({\rm pad}\), \(r\) の 3 つのコンポーネントが与えられると \((N,d)\) に対する SPONGE\([f,{\rm pad},r]\) 関数は Algorithm 8 によって規定される。幅 \(b\) は \(f\) の選択によって決まる。
アルゴリズム 8: SPONGE-\([f,{\rm pad},r]\)
入力: 列 \(N\), 非負整数 \(d\)
出力: \({\rm len}(Z)=d\) となるような列 \(Z\)
ステップ:
- \(P=N\,||\,{\rm pad}(r,{\rm len}(N))\) とする。
- \(n={\rm len}(P)/r\) とする。
- \(c=b-r\) とする。
- \(P_0,\ldots,P_{n-1}\) を \(P=P_0\,||\,\ldots\,||\,P_{n-1}\) となるように長さ \(r\) の列の一意なシーケンスとする。
- \(S={\tt 0}^b\) とする。
- 0 から \(n-1\) までの \(i\) に対して \(S=f(S \oplus (P_i\,||\,{\tt 0}^c))\) とする。
- \(Z\) を空の列とする。
- \(Z = Z\,||\,{\rm Trunc}_r(S)\) とする。
- \(d \le |Z|\) であれば \({\rm Trunc}_d(Z)\) を返し、そうでなければ続行する
- \(S=f(S)\) とし、ステップ 8 に進む。
入力 \(d\) は Algorithm 8 が返すビット数を決定するが、その値には影響しないことに注意。原理的に出力は無限の列とみなすことができ、実際には希望する数の出力ビットが生成されると計算が停止する。
 5 Keccak
5 Keccak
Keccak は元々 [8] で定義されたスポンジ関数のファミリーである。マルチレートパディングと呼ばれる Keccak のパディングルールはセクション 5.1 で規定される。Keccak のパラメータと基本的な転置はセクション 5.2 に説明されており、Keccak 関数のより小さなファミリーである Keccak\([c]\) が明示的に規定されている。これはセクション 6 で SHA-3 関数を定義するのに十分である。
 5.1 pad10*1 の仕様
5.1 pad10*1 の仕様
アルゴリズム 9: pad10*1\((x,m)\)
入力: 正の整数 \(x\); 非負整数 \(m\)
出力: \(m+{\rm len}(P)\) が \(x\) の正の倍数となるような列 \(P\)
ステップ:
- \(j=(-m-2) \bmod x\) とする。
- \(P={\tt 1}\,||\,{\tt 0}^j\,||\,{\tt 1}\) を返す。
したがって "pad10*1" のアスタリスクは必要な長さの出力列を生成するために "0" ビットが省略または繰り返されることを示している。
 5.2 Keccak\([c]\) の仕様
5.2 Keccak\([c]\) の仕様
Keccak は基礎関数として Keccak-\(p[b,12+2\ell]\) 転置 (セクション 3.3 で定義)、パディングルールとして pad10*1 ( セクション 5.1 で定義) を使用するスポンジ関数のファミリーである。このファミリーは \(r+c\) が {25,50,100,200,400,800,1600}、つまり Table 1 において \(b\) に対する 7 つの値の一つとなるようなレート \(r\) と容量 \(c\) 任意の選択によってパラメータ化される。
\(b=1600\) のケースに限定すると Keccak ファミリーは Keccak\([c]\) と表記される。この場合、\(r\) は \(c\) の選択によって決定する。特に \[ {\rm K{\scriptstyle ECCAK}}[c] = {\rm SPONGE}[{\rm K{\scriptstyle ECCAK}}\mbox{-}p[1600,24],\mbox{pad10*1},1600-c] \] したがって、入力ビット列 \(N\) と出力長 \(d\) が与えられる。\[ {\rm K{\scriptstyle ECCAK}}[c](N,d) = {\rm SPONGE}[{\rm K{\scriptstyle ECCAK}}\mbox{-}p[1600,24],\mbox{pad10*1},1600-c](N,d) \]
 6 SHA-3 関数仕様
6 SHA-3 関数仕様
セクション 6.1 では 4 つの SHA-3 ハッシュ関数が定義されている。またセクション 6.2 では 2 つの SHA-3 XOF が定義されている。セクション 6.3 では中間関数の観点から各 SHA-3 XOF の代替定義を示している。
 6.1 SHA-3 ハッシュ関数
6.1 SHA-3 ハッシュ関数
メッセージ \(M\) が与えられたとき、4 つの SHA-3 ハッシュ関数は \(M\) に 2 ビットの接尾辞を付加し、出力長を指定することによってセクション 5.2 で規定された Keccak 関数から次のように定義される: \[ \begin{eqnarray*} \mbox{SHA3-224}(M) & = & {\rm K{\scriptstyle ECCAK}}[448](M \, || \, {\tt 01}, 224); \\ \mbox{SHA3-256}(M) & = & {\rm K{\scriptstyle ECCAK}}[512](M \, || \, {\tt 01}, 256); \\ \mbox{SHA3-384}(M) & = & {\rm K{\scriptstyle ECCAK}}[768](M \, || \, {\tt 01}, 384); \\ \mbox{SHA3-512}(M) & = & {\rm K{\scriptstyle ECCAK}}[1024](M \, || \, {\tt 01}, 512). \end{eqnarray*} \] いずれの場合も容量はダイジェスト長の 2 倍、すなはち \(c=2d\) であり、Keccak\([c]\) への結果的な入力 \(N\) は接尾辞が追加されたメッセージ、つまり \(N=M\,||\,{\tt 01}\) である。接尾辞はドメイン分離をサポートする。つまり Keccak\([c]\) への入力は、SHA-3 ハッシュ関数で生じる入力と、SHA-3 XOF で生じる入力、また将来定義されるかもしれない他のドメインを区別する。
 6.2 SHA-3 拡張可能出力関数
6.2 SHA-3 拡張可能出力関数
メッセージ \(M\) が与えられたとき、任意の出力長 \(d\) に対して \(M\) に 4 ビットの接尾辞を付加することによって、セクション 5.2 で規定された Keccak\([c]\) 関数から 2 つの SHA-3 XOF である SHAKE128 と SHAKE256 が定義される。\[ \begin{eqnarray*} \mbox{SHAKE128}(M,d) & = & {\rm K{\scriptstyle ECCAK}}[256](M \, || \, {\tt 1111}, d); \\ \mbox{SHAKE256}(M,d) & = & {\rm K{\scriptstyle ECCAK}}[512](M \, || \, {\tt 1111}, d). \end{eqnarray*} \] 追加ビット 1111 の目的についてはセクション 6.3 で説明する。
 6.3 SHA-3 拡張可能出力関数の代替定義
6.3 SHA-3 拡張可能出力関数の代替定義
RawSHAKE128、RawSHAKE256 と呼ばれる 2 つの追加スポンジ関数が、以下の Keccak\([c]\) のインスタンスとして定義される。ここで入力列を \(J\)、出力長を \(d\) で示す: \[ \begin{eqnarray*} \mbox{RawSHAKE128}(J,d) & = & {\rm K{\scriptstyle ECCAK}}[256](J \, || \, {\tt 11}, d), \\ \mbox{RawSHAKE256}(J,d) & = & {\rm K{\scriptstyle ECCAK}}[512](J \, || \, {\tt 11}, d). \end{eqnarray*} \] これらの関数はセクション 6.2 の定義と同等の SHAKE128 および SHAKE256 の代替定義を有効にする。特に \[ \begin{eqnarray*} \mbox{SHAKE128}(M,d) & = & \mbox{RawSHAKE128}(M \, || \, {\tt 11}, d), \\ \mbox{SHAKE256}(M,d) & = & \mbox{RawSHAKE256}(M \, || \, {\tt 11}, d). \end{eqnarray*} \] が成り立つ。Keccak\([c]\) への次の入力 \(N\) は、これらの入力 \(M\) と \(J\) のパディング結果である: \[ N = J \, || \, {\tt\bf 11} = M \, || \, {\tt\it 11} \, || \, {\tt\bf 11} \] 太字の接尾辞 (つまり \({\tt\bf 11}\)) はドメイン分離をサポートする。これは RawSHAKE128 および RawSHAKE256 から生じる Keccak\([c]\) への入力、および将来定義されるかも知れない他のドメインから生じる入力とを区別する。
斜体の接尾辞 (つまり \({\tt\it 11}\)) は RawSHAKE128 および RawSHAKE256 と Sakura 符号化スキーム [6] との互換性を提供する。このスキームは長いメッセージのダイジェストをより効率的に計算・更新するために並列処理を適用することのできるツリーハッシュ [7] バリアントの将来の開発を推進するものである。
Keccak\([c]\) の実行中、マルチレートパディングルールの規定に従って追加ビットが \(N\) に付加されることに注意。
 7 適合性
7 適合性
Keccak\(p[1600,24]\) 転置と、この転置の 6 つの SHA-3 モード ─ SHA3-224、SHA3-256、SHA3-384、SHA3-512、SHAKE128、SHAKE256 ─ の実装は暗号アルゴリズム検証プログラム [9] の支援の元でその標準への適合性をテストすることができる。
SHA3-224、SHA3-256、SHA3-384、SHA3-512 は承認された暗号論的ハッシュ関数である。暗号論的ハッシュ関数の認可された用途の一つは Keyed Message Authentication Code (HMAC) である。MHAC 仕様 [10] において \(B\) で示されるバイト単位の入力ブロックサイズは SHA-3 ハッシュ関数に対して以下の Table 3 に示されている5:
| ハッシュ関数 | SHA3-224 | SHA3-256 | SHA3-384 | SHA3-512 |
|---|---|---|---|---|
| ブロックサイズ (バイト) | 144 | 136 | 104 | 72 |
SHAKE128 および SHAKE256 は承認された XOF であり、その承認された用途は NIST Special Publications で規定される。これらの用途の一部は認証されたハッシュ関数の用途と重複する可能性があるが、セクション A.2 で説明する特性により、XOF はハッシュ関数としては承認されていない。
Keccak\(p[1600,24]\) 転置は SHA-3 関数などの承認された動作モードのコンテキストでの使用が承認されている。同様に、この標準で定義されている他の中間関数 ─ 例えば Keccak\([c]\), RawSHAKE128, RawSHAKE256 ─ は Keccak\(p\) 転置の承認された動作モードのコンテキストで承認される。
Keccak\(p[1600,24]\) 転置は他の用途で承認される可能性があり、また他の Keccak 転置も FIPS Publication または NIST Special Publication の中でその動作モードが開発され承認された場合に承認される可能性がある。
SHA-3 関数は空の列を含む任意のビット長のメッセージに対して定義される。SHA-3 関数の適合実装ではメッセージに対してサポートされるビット長のセットが制限される場合がある。同様に SHA-3 XOF の適合実装では出力長に対してサポートされる値のセットが制限される場合がある。どちらの場合もそのような制限は他の実装との相互運用性に影響を与える可能性がある。
この標準で規定されているすべての計算手順について、適合する実装では与えられた手順のセットを数学的に等価な手順のセットで置き換えることができる。言い換えれば、すべての入力に対して正しい出力を生成する異なる手段が許可されている。
- 5一般にスポンジ関数の入力ブロックサイズ (ビット) がそのレートになる。
 A セキュリティ
A セキュリティ
[8] の Keccak のセキュリティ特性似関する詳細な分析はハッシュ関数と拡張可能出力関数の SHA-3 ファミリーに適用される。SHA-3 ファミリーはスポンジ構造からもセキュリティ特性を継承している。これらの特性は [4] で詳細に分析されている。
ハッシュ関数の用途は多くの場合、衝突耐性、原像耐性、第二原像耐性を必要とする。これらの特性は SHA-3 ファミリーのハッシュ関数と XOF についてセクション A.1 で要約されている。XOF は密接に関連した出力を生成すると言う点でハッシュ関数とは異なる。この重要なセキュリティ上の考慮事項についてはセクション A.2 で説明する。
 A.1 サマリー
A.1 サマリー
この標準の発行時点での SHA-3 関数のセキュリティ強度を Table 4 にまとめる。SHA-1 関数と SHA-2 関数は比較のために含まれており、[11] の議論の一部と重複している。これは必要に応じて最新のセキュリティ情報を更新する。
| 関数 | 出力サイズ | ビット単位のセキュリティ強度 | ||
|---|---|---|---|---|
| 衝突 | 原像 | 第二原像 | ||
| SHA-1 | \(160\) | \(\lt 80\) | \(160\) | \(160-L(M)\) |
| SHA-224 | \(224\) | \(112\) | \(224\) | \(\min(224,256-L(M))\) |
| SHA-512/224 | \(224\) | \(112\) | \(224\) | \(224\) |
| SHA-256 | \(256\) | \(128\) | \(256\) | \(256-L(M)\) |
| SHA-512/256 | \(256\) | \(128\) | \(256\) | \(256\) |
| SHA-384 | \(384\) | \(192\) | \(384\) | \(384\) |
| SHA-512 | \(512\) | \(256\) | \(512\) | \(512-L(M)\) |
| SHA3-224 | \(224\) | \(112\) | \(224\) | \(224\) |
| SHA3-256 | \(256\) | \(128\) | \(256\) | \(256\) |
| SHA3-384 | \(384\) | \(192\) | \(384\) | \(348\) |
| SHA3-512 | \(512\) | \(256\) | \(512\) | \(512\) |
| SHAKE128 | \(d\) | \(\min(d/2,128)\) | \(\ge \min(d,128)\) | \(\min(d,128)\) |
| SHAKE256 | \(d\) | \(\min(d/2,256)\) | \(\ge \min(d,256)\) | \(\min(d,256)\) |
\(M\) に対する第二原像攻撃へのセキュリティ強度について、関数 \(L(M)\) は \(\lceil \log_2({\rm len}(M)/B) \rceil\) と定義される。ここで \(B\) は関数のブロック長をビット単位で表しており、SHA-1, SHA-244, SHA-256 の場合は \(B=512\)、SHA-512 の場合は \(B=1024\) である。
4 つの SHA-3 ハッシュ関数は SHA-2 関数の代替となるもので、衝突攻撃、原像攻撃、第二原像攻撃に対して対応する SHA-2 関数が提供する体制と同等以上の耐性を提供するように設計されている。SHA-3 関数は、同じ出力長のランダム関数が抵抗するような伸張攻撃などの他の攻撃にも耐性があるように設計されており、一般に出力までランダム関数と同じセキュリティ強度を提供する。
2 つの SHA-3 XOF は衝突攻撃、原像攻撃、第二原像攻撃、および要求された出力長のランダム関数で抵抗されるその他の攻撃に耐性があるように設計されており、SHAKE128 では 128 ビット、SHAKE256 では 256 ビットのセキュリティ強度まで対応する。出力長が \(d\) ビットのランダム関数は衝突攻撃に対して \(d/2\) ビットを超えるセキュリティを提供できず、原像攻撃、第二原像攻撃に対して \(d\) ビットを超えるセキュリティを提供できないため、Table 4 に記載されているように \(d\) が十分に小さいと SHAKE128 も SHAKE256 も提供するセキュリティがそれぞれ 128 ビットと 256 ビット未満の安全性となる。例えば \(d=224\) であれば SHAKE128 と SHAKE256 は 112 ビットの衝突耐性を提供するが、SHAKE128 は 128 ビット、SHAKE256 は 224 ビットと異なるレベルの原像耐性を提供する。
\(d \gt r+c/2\) であれば SHAKE128 と SHAKE256 はそれぞれ 128 ビット以上と 256 ビット以上の原像耐性を提供する。さらに \(d \gt 1600\) ならば原像攻撃はおそらく存在しない。
 A.2 拡張可能出力関数に関する追加的考察
A.2 拡張可能出力関数に関する追加的考察
XOF は任意の長さの出力を生成する柔軟性を提供する強力な新しい種類の暗号プリミティブである。技術的には固定の出力長を選択することで XOF をハッシュ関数として使用することが可能である。しかし XOF には関連する出力を生成する可能性がある。これはセキュリティアプリケーションやプロトコル、システムの設計者がハッシュ関数に期待していないかもしれない特性である。この特性は XOF のアプリケーション開発において考慮すべき重要な点である。
設計上、XOF の出力長波 XOF が生成するビットには影響しない。つまり出力長は関数への必須入力ではない。概念的には出力を無限の列にすることができ、関数を呼び出すアプリケーションやプロトコル、システムは単にその列の必要な初期ビット数を計算するだけである。したがって共通のメッセージに対して 2 つの異なる出力長が選択されると、2 つの出力は密接に関連する。例えば、任意の正の整数 \(d\) および \(e\)、また任意のメッセージ \(M\) が与えられたとき、\({\rm Trunc}_d({\rm SHAKE128}(M,d+e))\) は \({\rm SHAKE128}(M,d)\) と同一である。SHAKE256 でも同じ性質が成り立つ。
実際には 2 つの異なる SHA-3 関数がこの性質を示すことはないだろう。例えばランダムに選択されたメッセージ \(M\) に対して、3 つの関数の構造がほぼ同じであっても、SHA3-256\((M)\) が SHA3-224\((M)\) の拡張、または SHAKE128\((M,224)\) の拡張になることはほぼ確実にない。同じ宣言は FIPS 180-4 での SHA-512 の短縮バージョン (つまり SHA-512/256) を含む、以前に承認されたハッシュ関数にも適用される。
ただし、ハッシュ関数のダイジェストを連結したり切り詰めたりすることで任意の出力長を持つ関数を構築するような既存のメカニズムは一般的にこの特性を示す。
密接に関連する出力の可能性は、XOF を呼び出すアプリケーションやプロトコル、システムのセキュリティに影響を与える可能性がある。例えば \({\it keymaterial}\) として指定されたメッセージから 112 ビットのトリプル DES 鍵を導出することに二者が合意する素朴な (そして承認されていない) 方法は \({\rm SHAKE128}({\it keymaterial},{\it keylength})\) を計算することである。ここで \({\it keylength}\) は 112 である。しかし攻撃者が当事者の一方に \({\it keylength}\) に異なる値 (例えば 168 ビット) を使用させ、\({\it keymaterial}\) に同じ値を使用させることができた場合、両当事者は以下のような鍵を得ることになる: \[ \begin{eqnarray*} {\rm SHAKE128}({\it keymaterial},112) & = & {\tt\bf fg} \\ {\rm SHAKE128}({\it keymaterial},168) & = & {\tt\bf fgh} \end{eqnarray*} \] ここでダイジェストの太字は 56 ビット列、つまりトリプル DES 鍵の部分を表す。トリプル DES の構造上、これらの鍵は攻撃に対して脆弱である。
実際には XOF をキー導出関数 (KDF) として使用すると、導出キーの長さおよび/またはタイプを KDF へのメッセージ入力に組み込むことにより、関連する出力の可能性を排除することができる。この場合、KDF を使用する 2 つのユーザ間で導出する鍵のタイプや長さについて意見の相違や誤解が生じたとしても、ほぼ確実に関連する出力が発生することにはつながらない。
拡張ダイジェストに問題がある場合、より一般的な解決策はドメイン分離である。これにより出力ビット数に関係なく XOF の異なるインスタンスを作成し、異なる目的に合わせて調整できる。すべての SHA-3 関数は NIST が将来開発する可能性のある新しい個別のドメインのバリアントを許可するように設計されている。
 B 例
B 例
5 つのステップマッピングと 6 つの SHA-3 関数の例は NIST コンピュータセキュリティリソースセンターの Web サイトで入手できる: http://csrc.nist.gov/groups/ST/toolkit/examples.html
これらの例のビット列は 16 進数の列、つまり 16 進数 16 桁のシーケンスとして表現されている: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F、ここで A は 10 を表す数字、B は 11 を表す数字などである。
SHA-3 の例の入力および出力の 16 進数列をビット列として解釈する規則は、例のページにある他の関数の規則とは異なる。16 進数列と SHA-3 ビット列間の変換関数はセクション B.1 で規定されている。バイト配置されたメッセージでは、SHA-3 関数のパディングの 16 進数形式はセクション B.2 に記述されている。
これらのセクションで特定の 16 進数列は Courier New フォントで書かれ、その前には 0x というマーカーが付けられている。
 B.1 変換関数
B.1 変換関数
16 進数列からそれが表す SHA-3 列への (\(h2b\) で表される) 変換は Algorithm 10 で規定される。この関数は偶数桁の 16 進数列に対して定義されている。
アルゴリズム 10: \(h2b(H,n)\)
入力: ある正の整数 \(m\) に対して \(2m\) 桁からなる 16 進数列 \(H\); \(n \le 8m\) となるような正の整数 \(n\)
出力: \({\rm len}(S)=n\) となるようなビット列 \(S\)
ステップ:
- \(0\le i\lt 2m-1\) となるような各整数 \(i\) に対して、\(H_i\) を \(H\) の \(i\) 番目の 16 進数桁とする: \(H=\)\(H_0\,\)\(H_1\,\)\(H_2\,\)\(H_3\,\)\(\ldots\,\)\(H_{2m-2}\,\)\(H_{2m-1}\)
- \(0\le i\lt m\) となるような各 \(\) に対して:
- \(h_i = 16 \cdot H_{2i} + H_{2i+1}\) とする。
- \(b_{i0}\,\)\(b_{i1}\,\)\(b_{i2}\,\)\(b_{i3}\,\)\(b_{i4}\,\)\(b_{i5}\,\)\(b_{i6}\,\)\(b_{i7}\) を \(h_i=b_{i7}\cdot 2^7+\)\(b_{i6}\cdot 2^6+\)\(b_{i5}\cdot 2^5+\)\(b_{i4}\cdot 2^4+\)\(b_{i3}\cdot 2^3+\)\(b_{i2}\cdot 2^2+\)\(b_{i1}\cdot 2^1+\)\(b_{i0}\cdot 2^0\) となるような一意のビット列とする。
- \(0\le i\lt m\) および \(0\le j\lt 8\) となる各整数ペア \((i,j)\) に対して \(T[8i+j]=b_{ij}\) とする。
- \(S = {\rm Trunc}_n(T)\) を返す。
ステップ 1 では 16 進数のインデックスを定義する。ステップ 2a では 16 進数の各ペアが基数 16 として表す 0 から 255 の整数 (基数 10) に変換される。ステップ 2b ではステップ 2a の各整数がバイトとしてバイナリ表現に変換される。ステップ 3 ではバイトが 1 つの列に連結され、ステップ 4 で結果が希望するビット数に切り詰められる。
例えば \(H=\mbox{0x}{\tt A3}\,{\tt 2E}\) と \(n=14\) の場合、Algorithm 10 のステップ 1 と 2 で定義された中間値は以下の Table 5 に示される:
| \(H_0={\tt A}\) | \(H_1={\tt 3}\) | \(H_2={\tt 2}\) | \(H_3={\tt E}\) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(h_0=16\cdot 10+3=163=\) \(1\cdot 2^7+0\cdot 2^6+1\cdot 2^5+0\cdot 2^4+0\cdot 2^3+0\cdot 2^2+1\cdot 2^1+1\cdot 2^0\) |
\(h_1=16\cdot 2+14=46=\) \(0\cdot 2^7+0\cdot 2^6+1\cdot 2^5+0\cdot 2^4+1\cdot 2^3+1\cdot 2^2+1\cdot 2^1+0\cdot 2^0\) |
||||||||||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| \(b_{07}\) | \(b_{06}\) | \(b_{05}\) | \(b_{04}\) | \(b_{03}\) | \(b_{02}\) | \(b_{01}\) | \(b_{00}\) | \(b_{17}\) | \(b_{16}\) | \(b_{15}\) | \(b_{14}\) | \(b_{13}\) | \(b_{12}\) | \(b_{11}\) | \(b_{10}\) |
したがって \(T=b_{00}\,\)\(b_{01}\,\)\(b_{02}\,\)\(b_{03}\,\)\(b_{04}\,\)\(b_{05}\,\)\(b_{06}\,\)\(b_{07}\,\)\(b_{10}\,\)\(b_{11}\,\)\(b_{12}\,\)\(b_{13}\,\)\(b_{14}\,\)\(b_{15}\,\)\(b_{16}\,\)\(b_{17}=\) \({\tt 1100}\) \({\tt 0101}\) \({\tt 0111}\) \({\tt 0100}\) であり、ステップ 3 と 4 で説明したように \(S =\) \({\rm Trunc}_{14}(T) =\) \({\tt 1100}\) \({\tt 0101}\) \({\tt 0111}\) \({\tt 01}\) である。
出力列 \(S\) の長さ \(n\) が入力として明示的に指定されない場合、\(h2b(H)\) は \(h2b(H,8m)\) と定義される。つまり \(n\) は取り得る最大値が与えられる。
SHA-3 のビット列からそれを表す 16 進数列 (\(b2h\) と表記) への変換は Algorithm 11 で規定される。
アルゴリズム 11: \(b2h(S)\)
入力: ある正の整数 \(n\) に対して \(n\) ビットからなるビット列 \(S\)
出力: \(2\lceil n/8\rceil\) 桁からなる 16 進数列 \(H\)
ステップ:
- \(n={\rm len}(S)\) とする。
- \(T=S\,||\,{\tt 0}^{-n \bmod 8}\) および \(m=\lceil n/8 \rceil\) とする。
- \(0\le i \lt m\) および \(0\le j\lt 8\) となるような各整数ペア \((i,j)\) に対して \(b_{ij}=T[8i+j]\) とする。
- \(0\le i \lt m\) となる各整数 \(i\) に対して:
- \(h_i=b_{i7}\cdot 2^7+b_{i6}\cdot 2^6+b_{i5}\cdot 2^5+b_{i4}\cdot 2^4+b_{i3}\cdot 2^3+b_{i2}\cdot 2^2+b_{i1}\cdot 2^1+b_{i0}\cdot 2^0\) とする。
- \(H_{2i}\) と \(H_{2i+1}\) を \(h_i=16\cdot H_{2i}+H_{2i+1}\) となるような 16 進数桁とする。
- \(H=H_0\,H_1\,H_2\,H_3\,\ldots\,H_{2m-2}\,H_{2m-1}\) を返す。
SHA-3 コンペティションへの Keccak 提出のために [12] で指定された正式なビット再配置関数は、メッセージがバイトに配置されている場合、すなはち \(n\) が 8 の倍数の場合に同等の変換を行う。
 B.2 パディングビットの 16 進数形式
B.2 パディングビットの 16 進数形式
SHA-3 関数の場合、Keccak\([c]\) への入力列 \(N\) を生成するためにメッセージ \(M\) に 2 ビットまたは 4 ビットの接尾辞が付加され、マルチレートパディングルールの一部としてさらにビットが追加される。ほとんどのアプリケーションではメッセージはバイト単位で整列している。つまり非負整数 \(m\) に対して \({\rm len}(M)=8m\) である。この場合、メッセージに追加される \(q\) で表されるバイト総数は \(m\) とレート \(r\) によって以下のように決定される: \[ q = (r/8) - (m \bmod (r/8)) \] \(q\) の値はセクション B.1 で指定された変換関数にしたがってこれらのバイトの 16 進数形式を決定する。結果として得られるパディングされたメッセージは Table 5 にまとめられている:
| SHA-3 関数のタイプ | パディングバイト数 | パディングメッセージ |
|---|---|---|
| ハッシュ | \(q=1\) | \(M\,||\,\mbox{0x}{\tt 86}\) |
| ハッシュ | \(q=2\) | \(M\,||\,\mbox{0x}{\tt 0680}\) |
| ハッシュ | \(q\gt 2\) | \(M\,||\,\mbox{0x}{\tt 06}\,||\,\mbox{0x}{\tt 00}\,\ldots\,||\mbox{0x}{\tt 80}\) |
| XOF | \(q=1\) | \(M\,||\,\mbox{0x}{\tt 9F}\) |
| XOF | \(q=2\) | \(M\,||\,\mbox{0x}{\tt 1F80}\) |
| XOF | \(q\gt 2\) | \(M\,||\,\mbox{0x}{\tt 1F}\,||\,\mbox{0x}{\tt 00}\,\ldots\,||\mbox{0x}{\tt 80}\) |
Table 5 において "\(\mbox{0x}{\tt 00}\)" という表記は \(q-2\) 個の "ゼロ" バイトからなる列を示す。
 C オブジェクト識別子
C オブジェクト識別子
SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHAKE128, および SHAKE256 のオブジェクト識別子 (OID) は http://csrc.nist.gov/groups/ST/crypto_apps_infra/csor/algorithms.html に掲載されている。
 D References
D References
- Federal Information Processing Standards Publication 180-4, Secure Hash Standard (SHS), Information Technology Laboratory, National Institute of Standards and Technology, March 2012, http://csrc.nist.gov/publications/fips/fips180-4/fips-180-4.pdf.
- G. Bertoni, J. Daemen, M. Peeters, and G. Van Assche, The KECCAK SHA-3 submission, Version 3, January 2011, http://keccak.noekeon.org/Keccak-submission-3.pdf.
- The SHA-3 Cryptographic Hash Algorithm Competition, November 2007-October 2012, http://csrc.nist.gov/groups/ST/hash/sha-3/index.html.
- G. Bertoni, J. Daemen, M. Peeters, and G. Van Assche, Cryptographic sponge functions, January 2011, http://sponge.noekeon.org/CSF-0.1.pdf.
- Ethan Heilman to hash-forum@nist.gov, October 5, 2012, Hash Forum, http://csrc.nist.gov/groups/ST/hash/email_list.html.
- G. Bertoni, J. Daemen, M. Peeters, and G. Van Assche, SAKURA: a flexible coding for tree hashing, http://keccak.noekeon.org/Sakura.pdf.
- R. C. Merkle, A digital signature based on a conventional encryption function, Advances in Cryptology - CRYPTO '87, A Conference on the Theory Applications of Cryptographic Techniques, Santa Barbara, California, USA, 1987, 369-378.
- G. Bertoni, J. Daemen, M. Peeters, and G. Van Assche, The KECCAK reference, Version 3.0, January 2011, http://keccak.noekeon.org/Keccak-reference-3.0.pdf.
- NIST Cryptographic Algorithm Validation Program (CAVP), http://csrc.nist.gov /groups/STM/cavp/index.html.
- Federal Information Processing Standards Publication 198-1, The Keyed-Hash Message Authentication Code (HMAC), Information Technology Laboratory, National Institute of Standards and Technology, July 2008, http://csrc.nist.gov/publications/fips/fips198-1/ FIPS-198-1_final.pdf.
- NIST Special Publication 800-107 Revision 1: Recommendation for Using Approved Hash Algorithms, August 2012, http://csrc.nist.gov/publications/nistpubs/800-107-rev1/ sp800-107-rev1.pdf.
- G. Bertoni, J. Daemen, M. Peeters, G. Van Assche, and R. Van Keer, KECCAK implementation overview, January 2011, http://keccak.noekeon.org/Keccak- implementation-3.0.pdf.
翻訳抄
暗号論的ハッシュ関数である SHA-3、および可変長出力が可能な SHAKE に関する 2015 年の NIST 仕様。
- DWORKIN, Morris J. SHA-3 standard: Permutation-based hash and extendable-output functions. 2015.