鍵共有アルゴリズム
暗号技術における鍵共有 (key exchange) とは、共通の秘匿情報を持たない当事者間で公にされている情報のみを用いて、すべての当事者サイドで通信内容を保護するための共通の鍵を生成する方法。現代の暗号通信では通信の双方が共有鍵 (もしくはそのシード) を作成するために使用している。
派生技術
TLS
TLS での Static Diffie-Hellman は証明書を使用してサーバを認証するが、デフォルトではクライアントを認証せず、また前方秘匿性 (ある時点の鍵が漏洩したときに過去にさかのぼって解読できない特性) も提供しない。Ephemeral Diffie-Hellman は RSA などと組み合わせて接続の両方または一方を認証し、完全な前方秘匿性 (perfect forward secrecy
) を提供する。
楕円曲線 Diffie-Hellman
楕円曲線 Diffie-Hellman は楕円曲線の代数的特徴を利用して、より小さな鍵のサイズで同等レベルのセキュリティを実装可能にしている。例えば 224 ビットの楕円曲線鍵は 2048 ビットの RSA 鍵と同じベルのセキュリティを提供する。これにより鍵共有がより通信帯域やストレージをより効率的に使用することができる。
楕円曲線 Diffie-Hellman は楕円曲線の特性に依存していること以外は標準の Diffie-Hellman 鍵共有と同じアルゴリズムで動作する。
Station to Station プロトコル
Station to Station プロトコル (STS) は署名公開鍵を互いに交換している前提で暗号鍵の合意とエンティティ認証を提供する。従来の Diffie-Hellman に基づいたアルゴリズムの鍵共有である。STS は合意した鍵に対する中間者 (man-in-the-middle) 攻撃耐性を持ち、タイムスタンプを使用せず完全な前方秘匿性を持つ。
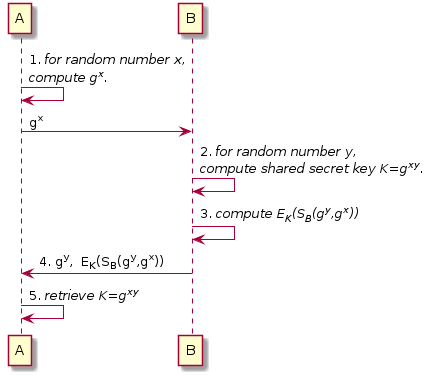
A と B がそれぞれお互いの公開鍵とパラメータ \(g\) を共有しているものとする。
- A: 乱数 \(x\) を選択して B に \(g^x\) を送信する。
- B: 乱数 \(y\) を選択し共有秘密鍵 \(K = g^{xy}\) を算出する。
- B: \((g^y, g^x)\) を自身の秘密鍵で署名し、署名を \(K\) で暗号化する。
- B: \(g^y\), \(E_K(S_B(g^y,g^x))\) を A に送信する。
- A: 共有秘密鍵 \(K = g^{xy}\) を算出し、署名を復号化して B の公開鍵で検証する。
- A: \((g^x, g^y)\) を自身の秘密鍵で署名し、署名を \(K\) で暗号化する。
- A: 暗号化した署名を B に送り、B は復号化して検証する。
DSA, ECDSA などの署名鍵は必ずしも非対称暗号や鍵共有をサポートしているわけではない点に注意。TLS の DHE 暗号スイートで使用されている証明書ベースのクライアント認証は STS の変化型である。