秘匿共通集合

Takami Torao #MPC #PSI #OPRF #セキュアマルチパーティ計算
  • このエントリーをはてなブックマークに追加

概要

秘匿共通集合 (PSI; private set intersection) は 2 つパーティ \(P_a\) と \(P_b\) がそれぞれで保持しているデータ集合 \(A\), \(B\) の共通集合 (交差) \(A \cap B\) を特定できる暗号技術。共通集合に含まれない要素の情報は相手に一切明かされないことから二者間のデータプライバシー保護が重要なケースにおいて有用な暗号技術である。

広告配信業者 \(P_a\) は広告を表示したユーザリスト \(A\) を持ち、加盟店 \(P_b\) は実際に商品を購入したユーザリスト \(B\) を持っている。このような状況で PSI を使うことで、互いのユーザリストの全体を明かすことなく広告を表示してから購入に至ったユーザ (つまり広告のコンバージョン率) を得ることができる [2]。

その他にも PSI の応用範囲は広く、例えば Apple や Google, Microsoft ではユーザの入力したパスワードが漏洩パスワードリストに含まれているかどうかを(ユーザ入力や漏洩リストを明かすことなく) 確認するために PSI を使用している。Common Friends [4] や PeerShare ではスマートフォンの電話帳から共通の知り合いを検索するスキームのコアブロックとして使われている (SNS ブームの 2010 年前後にはこのような友達リストから共通の知り合いを検索する SPI の応用がいくつか発表された)。他にも共通するヒトゲノム、ボットネットアクセスの検出、病院間で共通する患者の特定といった取り扱いに慎重を要するデータ検索への適用の提案が多くなされている。

PSI には多様なプロトコルがある。最近では暗号論的マルチパーティ計算の分野の一つとして活発に研究されている。また Microsoft Edge の漏洩パスワード検出は準同形暗号を使用した SPI である。一方で Signal の開発者は SPI では遅すぎると判断して Intel SGX を使用した trusted third-party を構築する方法を模索している。

現実的な適用では、相手の提出する (暗号化された) 集合が本当に正しいかの証明は SPI とは別に検討する必要がある。また [4] のように効率性のために Bloom フィルターなどを併用するケースが多く見られる。

Table of Contents

  1. 概要
  2. ナイーブハッシング
  3. 紛失疑似乱数関数を使う方法
  4. 参考文献

ナイーブハッシング

もっとも直感的な PSI はデータ集合の各要素をハッシュ化して交換する方法である。Alice と Bob がそれぞれデータ集合 \(A=\{a_1,\ldots,a_n\}\), \(B=\{b_1,\ldots,b_m\}\) を持っているとき、共通のハッシュ関数 \(h\) を用いて \(h:a_i \mapsto \alpha_i\), \(h:b_j \mapsto \beta_j\) のように変換し、\(\alpha_i=\beta_j\) となる要素を見つける。ここで Alice は \(\alpha_i\) に対する \(a_i\) を知っているため、共通要素の値を知ることができるが、それ以外の要素についての情報を得ることはできない。Bob についても同様である。

ナイーブハッシング方式の PSI はパーティの双方がいつでもハッシュ関数 \(h\) を利用できることからオフラインでのブルートフォース攻撃を行うことができる。このため集合を構成する要素のエントロピーが低い場合に安全ではない。一方で、他の PSI 手法より簡単かつ効率的であるため、現実的な適用では安全性を妥協してナイーブハッシング方式で構築することも少なくはない [2]。

紛失疑似乱数関数を使う方法

文献 [1] では紛失疑似乱数関数 (oblivious pseudorandom function; OPRF) を使って PSI の仕組みを説明している。この方法は一方のパーティでのみ暗号化 (ハッシュ化) を行うためオフラインでブルートフォース攻撃を行うことはできない。

OPRF は秘匿化 (ブラインド) された入力から秘匿化された乱数を生成する決定論的な疑似乱数関数である。ここで入力の秘匿化に使用したブラインドファクターを使わなければ乱数の値を解読できないという特徴がある。

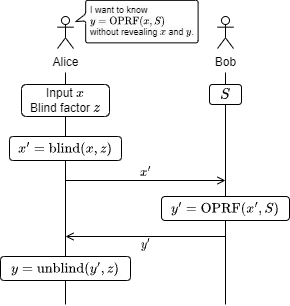
Fig 1 は Alice が入力 \(x\) を明かすことなく Bob の OPRF を使って乱数 \(y\) を得る操作を表している。

  1. Alice は入力 \(x\) とブラインドファクター \(z\) を使って秘匿化した \(x'\) を算出し Bob に送信する。

  2. Bob は鍵 \(S\) を使って \(x'\) から秘匿化された疑似乱数 \(y'\) を算出し Alice に送信する。

  3. Alice は \(x\) に対する疑似乱数 \(y\) をブラインドファクター \(z\) を使って \(y'\) から算出する。

H

ここで \(y = {\rm OPRF}(x,S) = {\rm unblind}({\rm OPRF}({\rm blind}(x, z), S), z)\) となることに注意。

この手順では Bob は Alice の入力値 \(x\) や乱数 \(y\) を知ることはできず、また Alice には Bob が使用した鍵 \(S\) を知ることもできない。文献 [1] の説明では \({\rm OPRF}()\) に HMAC に似た疑似乱数関数を想定している。

Oblivious Pseudo-Random Function
Fig 1. Alice が \(x\) を明かすことなく Bob の紛失疑似乱数関数を使って乱数 \(y\) を得る。

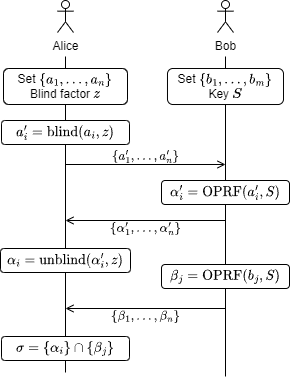
OPRF のスキームを使うと次のように互いのデータ集合を明かすことなく Alice が共通のデータを得ることができる。Fig 2 はこの一連の手順を表している。

  1. Alice はブラインドファクター \(z\) を使って自身のデータ集合 \(A=\{a_1,\ldots,a_n\}\) を秘匿化した \(A'=\{a'_1,\ldots,a'_n\}\) を算出し Bob に送信する。

  2. Bob は鍵 \(S\) を使って秘匿化されたデータ集合 \(A'\) から疑似乱数集合 \(\mathcal{A}'=\{\alpha'_1,\ldots,\alpha'_n\}\) を算出し Alice に送信する。

  3. Alice はブラインドファクター \(z\) を使って \(\mathcal{A}'\) から疑似乱数集合 \(\mathcal{A}=\{\alpha_1,\ldots,\alpha_n\}\) を算出する。

  4. Bob は鍵 \(S\) を使って自身のデータ集合 \(B=\{b_1,\ldots,b_m\}\) に対する疑似乱数集合 \(\mathcal{B}=\{\beta_1,\ldots,\beta_m\}\) を算出し Alice に送信する。

  5. Alice は \(A\) と \(B\) の共通要素を \(\mathcal{A} \cap \mathcal{B}\) によって知ることができる。

この手順では Alice のみがデータ集合の共通要素を知ることができる。

Private Set Intersection with OPRF
Fig 2. OPRF の PSI への応用。

コアブロックである OPRF の実装スキームは次のような方法がある [2]。

信頼できる第三者

OPRF は信頼できるサードパーティを導入し、ハードウェアトークンを使って構築することができる。

ブラインド RSA

また Blind-RSA を使って OPRF を構築できる。

楕円曲線

楕円曲線からの OPRF の構築は [3] で導入されている。

\(G\) を素数位数の巡回群とする。\(h\) を衝突耐性のあるハッシュ関数、\(S\) の保持する秘密鍵を \(k\)、\(C\) の保持する秘密入力を \(x\) とする。

参考文献

  1. David Wong. Real-World Cryptography. Manning (2021)
  2. PINKAS, Benny. SCHNEIDER, Thomas. ZOHNER, Michael. Scalable private set intersection based on OT extension. ACM Transactions on Privacy and Security (TOPS), 2018, 21.2: 1-35.
  3. JARECKI. Stanislaw. et al. Highly-efficient and composable password-protected secret sharing (or: How to protect your bitcoin wallet online). In: 2016 IEEE European Symposium on Security and Privacy (EuroS&P). IEEE, 2016. p. 276-291.
  4. Marcin Nagy, Emiliano De Cristofaro, Alexandra Dmitrienko, N. Asokan, and Ahmad-Reza Sadeghi. Do I know you? -- Efficient and Privacy-Preserving Common Friend-Finder Protocols and Applications. In: Proceedings of the 29th Annual Computer Security Applications Conference. 2013. p. 159-168.