セキュリティ
\( \def\vector#1{\boldsymbol{#1}} \)

論文翻訳: Curve25519: new Diffie-Hellman speed records

Takami Torao 2006年の論文 #楕円曲線暗号 #curve25519 #ed25519
  • このエントリーをはてなブックマークに追加
Daniel J. Bernstein \(\star\)
djb@cr.yp.to

Abstract

この論文では、例えば (いくつかの副次的な利点: 鍵圧縮なし、鍵検証なし、最先端のタイミング攻撃に対する保護ありという条件で) Pentium III での 832,457 サイクルという記録的な速度を達成する高セキュリティの楕円曲線 Diffie-Hellman 関数の設計と実装について説明する。これは (副次的利点の有無に拘らず) 同等と考えられるセキュリティレベルで他の著者による結果の 2 倍以上の速さである。

Table of Contents

  1. Abstract
  2. 1 導入
    1. 推奨されるセキュリティレベル
    2. 効率性
    3. 先行研究との比較
  3. 2 仕様
  4. 3 セキュリティ
    1. ユーザの責務
    2. 鍵派生関数の選択 [under construction]
    3. 攻撃者の力
    4. 簡単な攻撃概念
    5. rho 法とカンガルー法による一般的な離散対数
  5. 4 モジュロ \(2^{255}-19\) の高速演算
    1. バッチ離散対数
    2. 小部分群攻撃
    3. その他の攻撃
    4. \(2^{255}-19\) を法とする整数表現
    5. CPU 内の係数表現
    6. 浮動小数点演算の使用
    7. \(2^{255}-19\) を法とする整数の加算
    8. \(2^{255}-19\) を法とする整数の乗算
    9. 整数の選択
    10. なぜこの体か?
  6. 5 高速 Curve25519 計算
    1. 加算
    2. スカラー乗算
    3. その他の加算鎖
    4. なぜこの曲線か?
  7. References
  8. A 付録: 環、体と曲線
  9. B 付録: モンゴメリーの double-and-add 式
  10. 参照
キーワード: Diffie-Hellman, 楕円曲線 (elliptic curve), ポイント乗算 (point multiplication), 新しい曲線 (new curve), 新しいソフトウェア (new software), 高いと考えられるセキュリティ (high conjectured security), 高速 (high speed), 定数時間 (constant time), 短い鍵 (short key)

1 導入

この論文では、様々な暗号アプリケーションに適した最新の楕円曲線 Diffie-Hellman 関数である Curve25519 を紹介し分析する。この論文では Curve25519 を使用して高セキュリティ Diffie-Hellman 計算速度の新記録を取得する。

ここで Curve25519 のハイレベルのビューを示す: 各 Curve25519 ユーザは 32 バイトの秘密鍵と 32 バイトの公開鍵を持つ。2 人の Curve25519 ユーザのセットそれぞれには、2 人のユーザ間でのみメッセージの認証と暗号化に使用される 32 バイトの共通シークレットが存在する。

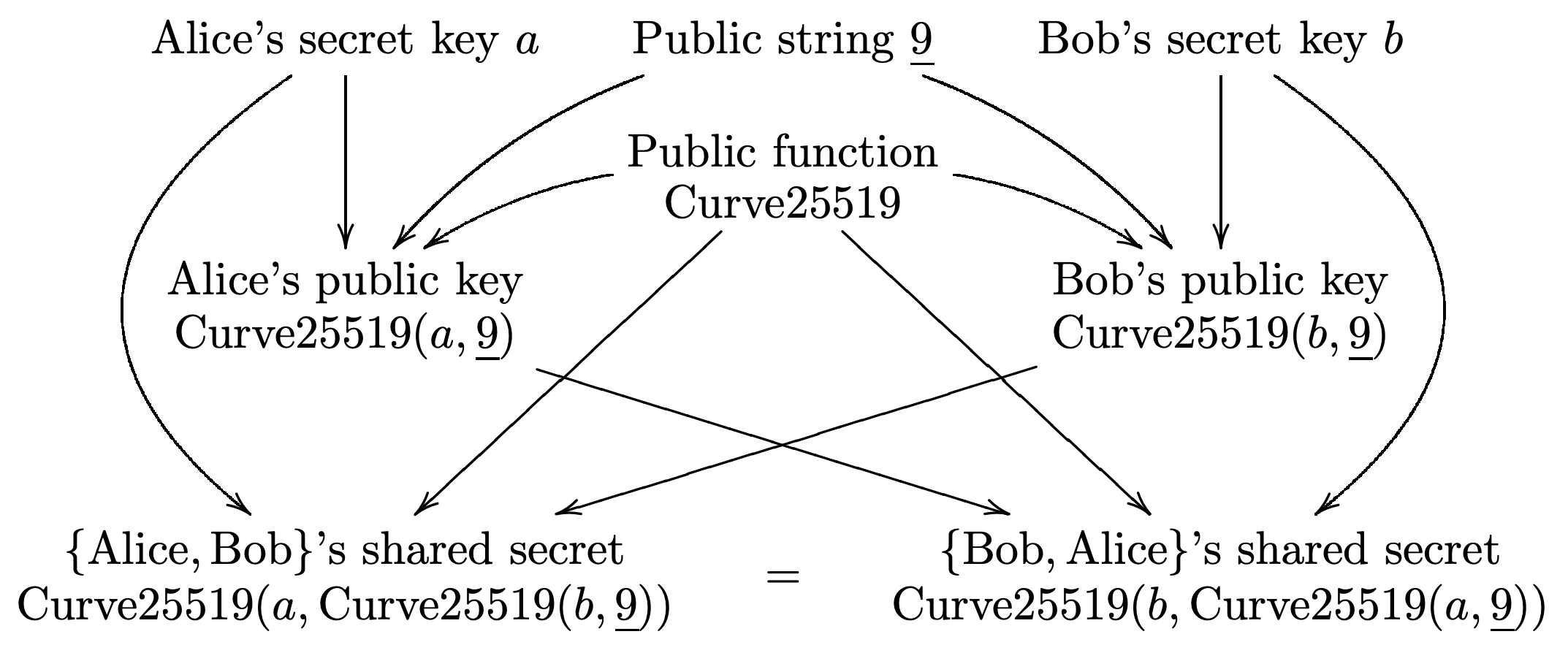
ミドルレベルのビュー: 以下の図は秘密鍵から公開鍵を介して共有シークレットまでのデータフローを示している。sｓ

共有シークレット \({\rm Curve25519}(a, {\rm Curve25519}(b, \underline{9}))\) のハッシュは秘密鍵認証システムの鍵として (メッセージ認証のために) 使用されるか、もしくは秘密鍵認証暗号システム (同様に暗号化とメッセージ認証のために) として使用される。

ローレベルビュー: Curve25519 関数は \({\bf F}_p\)-制限のある \(E({\bf F}_{p^2})\) 上の x 座標スカラー乗算である。ここで \(p\) は素数 \(2^{255}-19\) であり、\(E\) は楕円曲線 \(y^2 = x^3 + 486662x^2 + x\) である。詳細についてはセクション 2 を参照。

推奨されるセキュリティレベル

例えば 2 つの公開鍵から共有シークレットを算出するように、Curve25519 を破ることは非常に困難であると推測される。既知の攻撃はすべて、一般的な 128 ビットの秘密鍵暗号でブルートフォース検索を行うよりも高価である。

一般的な楕円曲線離散対数問題は 20 年にわたって攻撃され続けてきたがほとんど成功していない。一般的な離散対数アルゴリズムは十分に大きくない素数群を破るが、この論文で使用される素数群のサイズは \(2^{255}\) を超える。ある特別な代数構造を持つ楕円曲線は非ジェネリックアルゴリズムによってはるかに迅速に破ることができるが \(E({\bf F}_{p^2})\) にはそのような構造がない。Curve25519 関数のセキュリティに関する少佐なコメントはこの論文のセクション 3 を参照。

大量の量子コンピュータを構成すると Curve25519 を始めその他の全てのショート鍵離散対数システムが破壊される。一般的な楕円曲線離散対数アルゴリズムの詳細については [56] を参照。この観測結果の影響はこの論文のトピックとは直行しており、これ以上の説明は行わない。

効率性

私のパブリックドメインの Curve25519 ソフトウェアは Curve25519 関数の選択によっていくつかの効率的な機能を提供する:

  • 非常に高速。私のソフトウェアは Pentium III で 832,457 サイクル、Pentium 4 で 957,904 サイクル、Pentium M で 640,838 サイクル、Athlon で 624,786 サイクルで Curve25519 を計算する。これらの各数値は高セキュリティの Diffie-Hellman 機能の新速度記録である。私は UltraSPARC、PowerPC などの実装にも取り組んでおり、同様のサイクル数となると予想している。
  • 時間変動なし。暗号に関する文献のほとんどの速度報告はタイミング攻撃に対する保護のないソフトウェアに対するものだった。成功した攻撃については [12], [51] および [5] を参照。保護を導入すると計算が大幅に遅くなる可能性がある。対照的に Curve25519 ソフトウェアはハイパースレッディング攻撃やその他のキャッシュタイミング攻撃などのタイミング攻撃の影響を受けない。全ての入力依存分岐、全ての入力配列インデックス、および入力依存タイミングを持つほかの命令を回避している。
  • 短い秘密鍵。Curve25519 の秘密鍵は 32 バイトのみである。これは高セキュリティの Diffie-Hellman 関数の典型である。
  • 短い公開鍵。Curve25519 の公開鍵は 32 バイトのみである。典型的な楕円曲線 Diffie-Hellman 関数は 64 バイトの公開鍵を使用する。Miller が [46] で提案しているようにこれらのカギは半分のサイズに圧縮できるが、圧縮解除の時間は非常に顕著だが通常は報告されない。
  • 鍵検証フリー。ユーザが公開鍵の正当性を検証しなければ一般的な楕円曲線 Diffie-Hellman 関数は破られる可能性がある。例えば [14, セクション 4.1] および [3] を参照。鍵検証の時間は非常に顕著だが通常は報告されない。対照的に、全ての 32 バイトデータ列は Curve25519 公開鍵として受け入れることができる。
  • 短いコード。私のソフトウェアは非常に小さく、必要なすべてのテーブルを含むコンパイル済みコードはそれぞれの CPU で約 16 キロバイトであった。CPU の命令キャッシュで他のネットワークツールと簡単に統合することができる。

新速度記録はこの論文のハイライトである。セクション 4 と 5 では Curve25519 の計算についてボトムアップで説明する。

より低いセキュリティレベルの機能を選択することで速度を改善することができる。例えば 255 ビットから 160 ビットに落とすことができる。しかし、セクション 3 で説明するように、1 年未満で 160 ビットの楕円曲線を破るリソースを持つ攻撃者を想像することは容易である。ユーザはこのようなリスクにさらされるべきではない。代わりに最適なセキュリティレベルの Curve25519 に移行する必要がある。

もちろんユーザが大量のデータを交換する場合、ボトルネックは秘密鍵暗号システムであり Curve2559 の速度は問題にならない。

先行研究との比較

推測される様々なセキュリティレベルでの様々な Diffie-Hellman 機能の様々な実装の速度を分析する広範な文献が存在している。

特に、高セキュリティの楕円曲線スカラー乗算速度の報告がいくつかある: [17, Table 8] は体 (field)サイズ \(2^{256}-2^{224}+2^{192}+2^{96}-1\) に対して 400MHz Pentium II で 1,920,000 サイクルを報告している。また [33, Table 7] では部分体曲線を使用して体サイズ \(2^{283}\) に対して 400MHz Pentium II で 1,740,000 サイクルを報告している。[4, Table 4] ではランダム 256 ビット素体に対して 1000MHz Athlon で 3,086,000 サイクルを報告している。低セキュリティレベルにおいては、[7, Table3] では体サイズ \((231-1)^6\) に対して 233MHz Pentium MMX で 2,650,000 サイクルを報告している。[58, Table 4] では体サイズ \((2^{31}-1)^6\) に対して 166MHz Pentium Pro で 4,500,000 サイクルを報告している。[26, Table 6] では体サイズ \(2^{233}\) に対して 800MHz Pentium III で 1,720,000 サイクルを報告している。

Curve25519 の速度は上記の報告の 2 倍以上の速さである。Curve25519 の速度には鍵圧縮フリー、鍵検証フリー、および最先端のタイミング攻撃保護が含まれているが、上記の報告には含まれていないため、実際の比較はさらに偏るだろう。

私は以前に標準の NIST 曲線を使用してこの高速化の約半分を達成する予備的な実装作業を報告した。高速化の残り半分はより適切に設定された曲線への切り替えに依存している。この論文では高速化の両方の半分について説明する。

低レベルでは、楕円曲線 Diffie-Hellman 関数の設計と実装は速度に影響する多くの選択を行うことを意味している。いくつかの悪手を取ることでパフォーマンスを犠牲にする可能性がある。Curve25519 の設計と実装では選択シーケンス全体のグローバルな最適化を試みている:

  • 票数 (characteristic) 2 ではなく、大きな票数を使用する。
  • \(y^2 = x^3 - 3x + a_6\) ではなく、\((A-2)/4\) を持つ小さい曲線形状 \(y^2 = x^3 + Ax^2 + x\) を使用する。
  • \((x,y)\) ではなく \(x\) を公開鍵として使用する。
  • ツイスト上の鍵を禁止するために余計な時間をかけるのではなく、安全なツイストも持つ安全な曲線を使用する。
  • \((x/z,y/z)\) や \((x/z^2,y/z^3)\) ではなく、スカラー乗算内で \(x/z\) を使用する。
  • 変数配列のインデックス化を算術に変換する。
  • 秘密鍵の先頭 1 のために固定位置を使用する。
  • 秘密鍵に 2 の小さいべき乗を掛けて、曲線群とツイスト群の補因子を考慮する。
  • 拡大体 (extension field) ではなく素体 (prime field) を使用する。
  • ある \(b\) に対して \(2^b\) に非常に近い素数を使用する。
  • \(b/w\) が整数でなくてもある \(w\) に対して基数 \(2^{b/w}\) を使用する。
  • 各係数を可能な限り早く減らすのではなく、基数よりわずかに大きい係数を許可する。
  • 整数レジスタではなく、浮動小数点レジスタに係数を置く。それに応じて \(w\) を選択する。

詳細とクレジットについてはセクション 4 と 5 を参照。これらの選択は、設計と実装の多くのレベルで相互作用することに注意。例えば \((x/z^2,y/z^3)\) が \(x/z\) より優れている他の曲線形状や素数形状が存在する。このタイプの相互作用により、考えられる全ての選択肢が分かっている場合でも、適切な選択肢のシーケンスを特定することが難しくなる。

2 仕様

このセクションでは Cruve25519 関数を定義する。環、体、楕円曲線に精通していない読者は Appendix A と定理 2.1 の証明を参照。

定理 2.1 . \(p\) を \(p \ge 5\) となる素数、\(A\) を、\(A^2 - 4\) が \(p\) を法とする正方 (square) でない整数とする。\(E\) を体 \({\rm F}_p\) 上の楕円曲線 \(y^2 = x^3 + Ax^2 + x\)、\(X_0: E({\bf F}_{p^2}) \to {\bf F}_{p^2}\) を \(X_0(\infty)=0\)、\(X_0(x,y)=x\) と定義する。\(n\) を整数とする。\(q\) を \({\bf F}_p\) 上の元とする。このとき、\(X_0(Q)=q\) となるような全ての \(Q \in E({\bf F}_{p^2})\) に対して \(X_0(nQ) = s\) となる一意の \(s \in {\bf F}_p\) が存在する。

特に \(p\) を素数 \(2^{255}-19\)、\({\bf F}_p\) を素体 \({\bf Z}/p={\bf Z}/(2^{255}-19)\) として定義する。\(2\) が \({\bf F}_p\) において正方でないことに注意。\({\bf F}_{p^2}\) を体 \(({\bf Z}/(2^{255}-19))[\sqrt{2}]\)、\(A=486662\) と定義する。\(486662^2-4\) が \({\bf F}_p\) で正方でないことに注意。\(E\) を \({\bf F}_{p^2}\) 上の楕円曲線 \(y^2 = x^3 + Ax^2 + x\) として定義する。関数 \(X_0 : E({\bf F}_{p^2}) \to {\bf F}_{p^2}\) を \(X_0(\infty) = 0\)、\(X_0(x,y)=x\) と定義する。関数 \(X:E({\bf F}_{p^2}) \to \{\infty\} \cup {\bf F}_{p^2}\) を \(X(\infty)=\infty\)、\(X(x,y)=x\) と定義する。

この時点で、\(n \in 2^{254} + 8 \{0,1,2,3,\ldots,2^{251}-1\}\) および \(q \in {\bf F}_p\) が与えられると、Curve25519 関数は定理 2.1 によって \(s\) を生成すると言うことができる。ただし、暗号の現実と適合し [45] において Menezes が説明した設計エラーのタイプを捕らえるために、代わりに Curve25519 の入力と出力をバイトのシーケンスとして定義するつもりである。

バイト集合は定義より \(\{0,1,\ldots,255\}\) である。バイトをビットシーケンスとしてエンコードすることはこの文書では無関係である。\(\{0,1,\ldots,2^{256}-1\}\) から 32 バイト列の集合 \(\{0,1,\ldots,255\}^{32}\) への標準的なリトルエンディアンの全単射として \(s \mapsto \underline{s}\) と記述する。言い換えると、\(s \in \{0,1,\ldots, 2^{256}-1\}\) となる整数それぞれに対して \(\underline{s} = (s \bmod 256, \lfloor s/256 \rfloor \bmod 256, \ldots, \lfloor s/256^{31} \rfloor \bmod 256)\) を定義する。

Curve25519 公開鍵集合は定義より \(\{0,1,\ldots,255\}^{32}\) である。言い換えると \(\{\underline{q}: q \in \{0,1,\ldots,2^{256}-1\}\}\) である。Curve25519 秘密鍵集合は定義より \(\{0,8,16,24,\ldots,248\} \times \{0,1,\ldots,255\}^{30} \times \{64,65,66,\ldots,127\}\) である。言い換えると \(\{\underline{n}: n \in 2^{254} + 8 \{0,1,2,3,\ldots,2^{251}-1\}\}\) である。

今 \({\rm Curve25519}:\{\mbox{Curve25519 secret keys}\} \times \{\mbox{Curve25519 public keys}\} \to \{\mbox{Curve25519 public keys}\}\) は固定値 \(q \in \{0,1,\ldots,2^{256}-1\}\) と \(n \in 2^{254} + 8\{0,1,2, \ldots,2^{251}-1\}\) として定義される。定理 2.1 によって \(X_0(Q) = q \bmod 2^{255}-19\) となるような \(s = X_0(nQ)\) の特性を持つ一意の整数 \(s \in \{0,1,2,\ldots, 2^{255}-20\}\) が存在する。最後に、\({\rm Curve25519}(\underline{n},\underline{q})\) は \(\underline{s}\) として定義される。\({\rm Curve25519}\) は全射でないことに注意。特に最終出力ビットは常に 0 であり転送する必要はない。

3 セキュリティ

このセクションでは Curve25519 に対する攻撃について説明する。結論として、既知の攻撃は全て非常に高価である。

ユーザの責務

合法的なユーザは独立した一様乱数で秘密鍵を生成すると想定される。例えばユーザは 32 バイト列の一様乱数を生成し、最初のバイトの 0, 1, 2 ビット目をクリアし、最後のバイトの 7 ビット目をクリアし、最後のバイトの 6 ビット目を設定できる。

均一性からの大きな逸脱はあらゆるセキュリティを無効化する。例えば、秘密鍵 \(\underline{n}\) の最初の 16 バイトが公の定数として選択された場合、過度に大きな演算によって公開鍵 \({\rm Curve25519}(\underline{n},\underline{9})\) から \(\underline{n}\) の残りのバイトが推測される。これは Curve25519 の問題ではなく、ユーザは鍵に十分なランダム性を設定する責任がある。

合法的なユーザは秘密鍵を秘密にしておくことも想定される。これは、公開鍵 \({\rm Curve25519}(\underline{u},\underline{9})\) を計算し、与えられた \(\underline{q}\) に対する秘密共有ハッシュ \(H({\rm Curve25519}(\underline{n},\underline{q}))\) を計算する場合を除いて、秘密鍵 \(\underline{n}\) が使用されないことを意味している。

ユーザは単一の \(\underline{q}\) の後に \(\underline{n}\) を捨てることは想定されていない。Diffie-Hellman 秘密鍵は [23, Section 3] で述べられているように多くの公開鍵で再利用することができる (効率を上げるためにそうすべきである)。各ユーザの秘密鍵 \(\underline{n}\) は、多くの他のユーザの公開鍵 \(\underline{q_1}, \underline{q_2},\underline{q_3},\ldots\) と組み合わせられ、秘密共有ハッシュ \(H({\rm Curve25519}(\underline{n}, \underline{q_1})), H({\rm Curve25519}(\underline{n}, \underline{q_2})), H({\rm Curve25519}(\underline{n}, \underline{q_3})), \ldots\) を生成する。

鍵派生関数の選択

攻撃者の力

簡単な攻撃概念

rho 法とカンガルー法による一般的な離散対数

4 モジュロ \(2^{255}-19\) の高速演算

このセクションでは一般的な CPU 命令、特に浮動小数点命令を使用して \(p=2^{255}-19\) の体 \({\bf F}_p\) における乗算と加算を素早く計算する方法について説明する。具体的な CPU として Pentium M に焦点を当てているが、同じ手法は様々な CPU でも機能するだろう。このセクションでは体の構造の選択と素数の選択についても説明する。

このセクションでは "浮動小数点" を "fp" と省略する。

バッチ離散対数

小部分群攻撃

その他の攻撃

\(2^{255}-19\) を法とする整数表現

CPU 内の係数表現

浮動小数点演算の使用

\(2^{255}-19\) を法とする整数の加算

\(2^{255}-19\) を法とする整数の乗算

整数の選択

なぜこの体か?

5 高速 Curve25519 計算

このセクションでは楕円曲線 \(y^2 = x^3 + 486662x^2 + x\) での高速な x 座標点の加算とスカラー乗算、つまり Curve25519 の高速演算について説明し、この曲線を他の楕円曲線と比較する。

セクション 2 で 2 つの x 座標関数を定義している。片方の関数 \(X_0\) は \(\infty\) を 0 にマップし、もう一つの関数 \(X\) は \(\infty\) を \(\infty\) にマップ為る。Curve25519 は \(X_0\) を使って定義されているが、演算中は最後の瞬間まで \(X\) を使うと便利である。

加算

スカラー乗算

その他の加算鎖

なぜこの曲線か?

References

  1. — (no editor), 17th annual symposium on foundations of computer science, IEEE Computer Society, Long Beach, California, 1976. MR 56:1766. See [52].
  2. Kazimierz Alster, Jerzy Urbanowicz, Hugh C. Williams (editors), Public-key cryptography and computational number theory: proceedings of the international conference held in Warsaw, September 11–15, 2000, Walter de Gruyter, Berlin, 2001. ISBN 3–11–017046–9. MR 2002h:94001. See [60].
  3. Adrian Antipa, Daniel Brown, Alfred Menezes, René Struik, Scott Vanstone, Validation of elliptic curve public keys, in [21] (2003), 211–223. MR 2171928. Citations in this paper: §1.
  4. Roberto M. Avanzi, Aspects of hyperelliptic curves over large prime fields in software implementations, in [36] (2004), 148–162. Citations in this paper: §1, §5.
  5. Roberto M. Avanzi, Generic algorithms for computing discrete logarithms, in [19] (2005), 477–494. MR 2162735. Citations in this paper: §3, §3.
  6. Roberto M. Avanzi, Preda Mihăilescu, Generic efficient arithmetic algorithms for PAFFs (processor adequate finite fields) and related algebraic structures (extended abstract), in [43] (2004), 320–334. Citations in this paper: §4.
  7. Daniel V. Bailey, Christof Paar, Efficient arithmetic in finite field extensions with application in elliptic curve cryptography, Journal of Cryptology 14 (2001), 153–176. ISSN 0933–2790. Citations in this paper: §1, §4.
  8. Mihir Bellare (editor), Advances in cryptology—CRYPTO 2000: proceedings of the 20th Annual International Cryptology Conference held in Santa Barbara, CA, August 20–24, 2000, Lecture Notes in Computer Science, 1880, Springer-Verlag, Berlin, 2000. ISBN 3–540–67907–3. MR 2002c:94002. See [14].
  9. Andreas Bender, Guy Castagnoli, On the implementation of elliptic curve cryptosystems, in [16] (1990), 186–192. MR 91d:11154. Citations in this paper: §4.
  10. Kamel Bentahar, The equivalence between the DHP and DLP for elliptic curves used in practical applications, revisited (2005). URL: http://eprint.iacr.org/2005/307. Citations in this paper: §3.
  11. Daniel J. Bernstein, The Poly1305-AES message-authentication code, in [32] (2005), 32–49. URL: http://cr.yp.to/papers.html#poly1305. ID 0018d9551b5546d97c340e0dd8cb5750. Citations in this paper: §4.
  12. Daniel J. Bernstein, Cache-timing attacks on AES (2005). URL: http://cr.yp.to/ papers.html#cachetiming. ID cd9faae9bd5308c440df50fc26a517b4. Citations in this paper: §1, §4.
  13. Daniel J. Bernstein, Salsa20 specification (2005). URL: http://cr.yp.to/ snuffle.html. Citations in this paper: §3.
  14. Ingrid Biehl, Bernd Meyer, Volker Muller, ¨ Differential fault attacks on elliptic curve cryptosystems (extended abstract), in [8] (2000), 131–146. URL: http://lecturer. ukdw.ac.id/vmueller/publications.php. Citations in this paper: §1, §3.
  15. Colin Boyd (editor), Advances in cryptology—ASIACRYPT 2001: proceedings of the 7th international conference on the theory and application of cryptology and information security held on the Gold Coast, December 9–13, 2001, Lecture Notes in Computer Science, 2248, Springer-Verlag, Berlin, 2001. ISBN 3–540–42987–5. MR 2003d:94001. See [59].
  16. Gilles Brassard (editor), Advances in cryptology—CRYPTO ’89, Lecture Notes in Computer Science, 435, Springer-Verlag, Berlin, 1990. ISBN 0–387–97317–6. MR 91b:94002. See [9].
  17. Michael Brown, Darrel Hankerson, Julio L´opez, Alfred Menezes, Software implementation of the NIST elliptic curves over prime fields (2000); see also newer version [18]. URL: http://www.cacr.math.uwaterloo.ca/techreports/ 2000/corr2000-56.ps. Citations in this paper: §1, §5.
  18. Michael Brown, Darrel Hankerson, Julio L´opez, Alfred Menezes, Software implementation of the NIST elliptic curves over prime fields, in [49] (2001), 250–265; see also older version [17]. MR 1907102.
  19. Henri Cohen, Gerhard Frey (editors), Handbook of elliptic and hyperelliptic curve cryptography, CRC Press, 2005. ISBN 1–58488–518–1. See [5], [24], [25], [30].
  20. Yvo Desmedt (editor), Advances in cryptology—CRYPTO ’94, Lecture Notes in Computer Science, 839, Springer-Verlag, Berlin, 1994. See [44].
  21. Yvo Desmedt, Public Key Cryptography—PKC 2003, 6th international workshop on theory and practice in public key cryptography, Miami, FL, USA, January 6– 8, 2003, proceedings, Lecture Notes in Computer Science, 2567, Springer, Berlin, 2003. ISBN 3–540–00324–X. See [3].
  22. Claus Diem, The GHS attack in odd characteristic, Journal of the Ramanujan Mathematical Society 18 (2003), 1–32. MR 2004a:14030. URL: http://www.math. uni-leipzig.de/~diem/preprints. Citations in this paper: §4.
  23. Whitfield Diffie, Martin Hellman, New directions in cryptography, IEEE Transactions on Information Theory 22 (1976), 644–654. ISSN 0018–9448. MR 55:10141. URL: http://cr.yp.to/bib/entries.html#1976/diffie. Citations in this paper: §3.
  24. Christophe Doche, Tanja Lange, Arithmetic of elliptic curves, in [19] (2005), 267– 302. MR 2162729. Citations in this paper: §A.
  25. Christophe Doche, Tanja Lange, Arithmetic of special curves, in [19] (2005), 355– 387. MR 2162731. Citations in this paper: §4.
  26. Kenny Fong, Darrel Hankerson, Julio L´opez, Alfred Menezes, Field inversion and point halving revisited (2003); see also newer version [27]. URL: http://www. cacr.math.uwaterloo.ca/techreports/2003/tech reports2003.html. Citations in this paper: §1.
  27. Kenny Fong, Darrel Hankerson, Julio L´opez, Alfred Menezes, Field inversion and point halving revisited, IEEE Transactions on Computers 53 (2004), 1047–1059; see also older version [26]. ISSN 0018–9340.
  28. Jens Franke, Thorsten Kleinjung, Christof Paar, Jan Pelzl, Christine Priplata, Martin Simka, Colin Stahlke, An efficient hardware architecture for factoring integers with the elliptic curve method, Workshop Record of SHARCS 2005 (2005), 51–62. URL: http://www.best.tuke.sk/simka/pub.html. Citations in this paper: §3, §3.
  29. Gerhard Frey, How to disguise an elliptic curve (Weil descent) (1998). URL: http://www.cacr.math.uwaterloo.ca/conferences/1998/ecc98/slides. html. Citations in this paper: §4.
  30. Gerhard Frey, Tanja Lange, Transfer of discrete logarithms, in [19] (2005), 529–543. MR 2162738. Citations in this paper: §3.
  31. Robert P. Gallant, Robert J. Lambert, Scott A. Vanstone, Faster point multiplication on elliptic curves with efficient endomorphisms, in [38] (2001), 190–200. MR 2003h:14043. Citations in this paper: §5.
  32. Henri Gilbert, Helena Handschuh (editors), Fast software encryption: 12th international workshop, FSE 2005, Paris, France, February 21–23, 2005, revised selected papers, Lecture Notes in Computer Science, 3557, Springer, 2005. ISBN 3–540– 26541–4. See [11].
  33. Darrel Hankerson, Julio Lopez Hernandez, Alfred Menezes, Software implementation of elliptic curve cryptography over binary fields (2000); see also newer version [34]. URL: http://www.cacr.math.uwaterloo.ca/techreports/ 2000/corr2000-42.ps. Citations in this paper: §1.
  34. Darrel Hankerson, Julio Lopez Hernandez, Alfred Menezes, Software implementation of elliptic curve cryptography over binary fields, in [40] (2000), 1–24; see also older version [33].
  35. Darrel Hankerson, Alfred Menezes, Scott Vanstone, Guide to elliptic curve cryptography, Springer, New York, 2004. ISBN 0–387–95273–X. MR 2054891. Citations in this paper: §4.
  36. Marc Joye, Jean-Jacques Quisquater (editors), Cryptographic hardware and embedded systems—CHES 2004: 6th international workshop, Cambridge, MA, USA, August 11–13, 2004, proceedings, Lecture Notes in Computer Science, 3156, Springer, 2004. ISBN 3–540–22666–4. See [4].
  37. Burton S. Kaliski Jr. (editor), Advances in cryptology—CRYPTO ’97: 17th annual international cryptology conference, Santa Barbara, California, USA, August 17– 21, 1997, proceedings, Lecture Notes in Computer Science, 1294, Springer, 1997. ISBN 3–540–63384–7. MR 99a:94041. See [42].
  38. Joe Kilian (editor), Advances in cryptology: CRYPTO 2001, 21st annual international cryptology conference, Santa Barbara, California, USA, August 19–23, 2001, proceedings, Lecture Notes in Computer Science, 2139, Springer, 2001. ISBN 3–540–42456–3. MR 2003d:94002. See [31].
  39. Neal Koblitz, Alfred J. Menezes, Another look at “provable security” (2004). URL: http://www.cacr.math.uwaterloo.ca/~ajmeneze/publications/ provable.pdf. Citations in this paper: §3.
  40. C¸ etin Kaya Ko¸c, Christof Paar, Cryptographic hardware and embedded systems— CHES 2000: Proceedings of the 2nd International Workshop held in Worcester, MA, USA, August 2000, Lecture Notes in Computer Science, Springer, 2000. ISBN 3–540–42521–7. See [34].
  41. Fabian Kuhn, Rene Struik, Random walks revisited: extensions of Pollard’s rho algorithm for computing multiple discrete logarithms, in [64] (2001), 212–229. URL: http://www.distcomp.ethz.ch/publications.html. Citations in this paper: §3.
  42. Chae Hoon Lim, Pil Joong Lee, A key recovery attack on discrete log-based schemes using a prime order subgroup, in [37] (1997), 249–263. URL: http:// dasan.sejong.ac.kr/~chlim/english pub.html. Citations in this paper: §3, §3.
  43. Mitsuru Matsui, Robert Zuccherato (editors), Selected areas in cryptography: 10th annual international workshop, SAC 2003, Ottawa, Canada, August 14–15, 2003, revised papers, Lecture Notes in Computer Science, 3006, Springer, 2004. ISBN 3–540–21370–8. See [6].
  44. Ueli M. Maurer, Towards the equivalence of breaking the Diffie-Hellman protocol and computing discrete logarithms, in [20] (1994), 271–281. URL: http://www. crypto.ethz.ch/~maurer/publications.html. Citations in this paper: §3.
  45. Alfred Menezes, Another look at HMQV (2005). URL: http://eprint.iacr.org/ 2005/205. Citations in this paper: §2.
  46. Victor S. Miller, Use of elliptic curves in cryptography, in [65] (1986), 417–426. MR 88b:68040. Citations in this paper: §1.
  47. Peter L. Montgomery, Speeding the Pollard and elliptic curve methods of factorization, Mathematics of Computation 48 (1987), 243–264. ISSN 0025–5718. MR 88e:11130. URL: http://cr.yp.to/bib/entries.html#1987/montgomery. Citations in this paper: §5.
  48. A. Muzereau, Nigel P. Smart, Frederik Vercauteren, The equivalence between the DHP and DLP for elliptic curves used in practical applications, LMS Journal of Computation and Mathematics 7 (2004), 50–72. URL: http://www.lms.ac.uk/ jcm/7/lms2003-034/. Citations in this paper: §3.
  49. David Naccache (editor), Topics in cryptology—CT-RSA 2001: Proceedings of the Cryptographers’ Track at the RSA Conference held in San Francisco, CA, April 8–12, 2001, Lecture Notes in Computer Science, 2020, Springer, 2001. ISBN 3– 540–41898–9. MR 2003a:94039. See [18].
  50. Dag Arne Osvik, Adi Shamir, Eran Tromer, Cache atacks and countermeasures: the case of AES (extended version) (2005). URL: http://www.wisdom.weizmann. ac.il/~tromer/. Citations in this paper: §1.
  51. Colin Percival, Cache missing for fun and profit (2005). URL: http://www. daemonology.net/hyperthreading-considered-harmful/. Citations in this paper: §1.
  52. Nicholas Pippenger, On the evaluation of powers and related problems (preliminary version), in [1] (1976), 258–263; newer version split into [53] and [54]. MR 58:3682. URL: http://cr.yp.to/bib/entries.html#1976/pippenger. Citations in this paper: §5.
  53. Nicholas Pippenger, The minimum number of edges in graphs with prescribed paths, Mathematical Systems Theory 12 (1979), 325–346; see also older version [52]. ISSN 0025–5661. MR 81e:05079. URL: http://cr.yp.to/bib/entries.html# 1979/pippenger.
  54. Nicholas Pippenger, On the evaluation of powers and monomials, SIAM Journal on Computing 9 (1980), 230–250; see also older version [52]. ISSN 0097–5397. MR 82c:10064. URL: http://cr.yp.to/bib/entries.html#1980/pippenger.
  55. John M. Pollard, Kangaroos, Monopoly and discrete logarithms, Journal of Cryptology 13 (2000), 437–447. ISSN 0933–2790. Citations in this paper: §3.
  56. John Proos, Christof Zalka, Shor’s discrete logarithm quantum algorithm for elliptic curves (2003). URL: http://www.cacr.math.uwaterloo.ca/techreports/2003/ tech reports2003.html. Citations in this paper: §1.
  57. Nigel P. Smart, A comparison of different finite fields for use in elliptic curve cryptosystems (2000); see also newer version [58]. URL: http://www.cs.bris.ac. uk/Publications/pub info.jsp?id=1000458.
  58. Nigel P. Smart, A comparison of different finite fields for elliptic curve cryptosystems, Computers and Mathematics with Applications 42 (2001), 91–100; see also older version [57]. MR 2002c:94033. Citations in this paper: §1.
  59. Martijn Stam, Arjen K. Lenstra, Speeding up XTR, in [15] (2001), 125–143. MR 2003h:94049. Citations in this paper: §5.
  60. Edlyn Teske, Square-root algorithms for the discrete logarithm problem (a survey), in [2] (2001), 283–301. MR 2003c:11156. URL: http://www.cacr.math.uwaterloo. ca/~eteske/publications.html. Citations in this paper: §3.
  61. Edlyn Teske, Computing discrete logarithms with the parallelized kangaroo method (2001); see also newer version [62]. URL: http://www.cacr.math.uwaterloo.ca/ techreports/2001/tech reports2001.html. Citations in this paper: §3.
  62. Edlyn Teske, Computing discrete logarithms with the parallelized kangaroo method, Discrete Applied Mathematics 130 (2003), 61–82; see also older version [61]. MR 2004h:11112.
  63. Paul C. van Oorschot, Michael Wiener, Parallel collision search with cryptanalytic applications, Journal of Cryptology 12 (1999), 1–28. ISSN 0933–2790. URL: http://members.rogers.com/paulv/papers/pubs.html. Citations in this paper: §3.
  64. Serge Vaudenay, Amr M. Youssef (editors), Selected areas in cryptography: 8th annual international workshop, SAC 2001, Toronto, Ontario, Canada, August 16– 17, 2001, revised papers, Lecture Notes in Computer Science, 2259, Springer, 2001. ISBN 3–540–43066–0. MR 2004k:94066. See [41].
  65. Hugh C. Williams (editor), Advances in cryptology: CRYPTO ’85, Lecture Notes in Computer Science, 218, Springer, Berlin, 1986. ISBN 3–540–16463–4. See [46].

A 付録: 環、体と曲線

この付録では定理 2.1 の一般性のレベルで楕円曲線をレビューする。楕円曲線に関する詳細は [24, Chapter 13] を参照。

基礎体 (the base field)

\(p\) を \(p \ge 5\) となる素数とする。\({\bf F}_p\) を集合 \(\{0,1,\ldots,p-1\}\)、\({\bf F}_p\) の二項演算子 + を (加算値 \(\bmod p\))、二項演算子 \(\cdot\) を (乗算値 \(\bmod p\))、単項演算子 \(-\) を (否定値 \(\bmod p\)) と定義する。

\({\bf F}_p\) は \(0\), \(1\), \(-\), \(+\), \(\cdot\) の下で可換環である。これは \({\bf Z}\) により、例えば恒等式 \(a(b+c+1)=ab+ac+a\) のように \(0\), \(1\), \(-\), \(+\), \(\cdot\) のそれぞれの恒等式が満たされることを意味している。さらに、\(p\) が素数であるため \({\bf F}_p\) は体である。\({\bf F}_p\) の全ての非ゼロ元は \({\bf F}_p\) に逆数を持つ。

基礎体における正方 (squares in the base field)

正方は \({\bf F}_p\) の非ゼロ元上の 2 対 1 マップであるため、\({\bf F}_p\) には正確に \((p-1)/2\) の非正方が存在する。\({\bf F}_p\) 内で正方でない最小の \(\delta \in \{1,2,\ldots,p-1\}\) を求めよ。

フェルマーの小定理は、\(\alpha\) が \({\bf F}_p\) における非ゼロの正方であれば \(\alpha^{(p-1)/2} = 1\) であり、\(\alpha=0\) であれば \(\alpha^{(p-1)/2} = 0\) であることを暗に示している。従って、もし \(\alpha\) が \({\bf F}_p\) において非正方であれば \(\alpha/\delta\) は \({\bf F}_p\) において非ゼロの正方である。

拡大体 (the extension field)
楕円曲線 (the elliptic curve)
定理 2.1 の証明

B 付録: モンゴメリーの double-and-add 式

参照

通常の楕円曲線アルゴリズム (EC) より高速で鍵の小さい Curve25519 を使用した暗号計算に関する 2006 年の論文。

  1. Daniel J. Bernstein (2006) "Curve25519: new Diffie-Hellman speed records"