\( \def\vector#1{\boldsymbol{#1}} \)

秘密分散共有

2019年11月3日 (since 2017年12月28日) #SecretSharing #VSS

概要

秘密分散共有 (secret sharing) または単に秘密分散は秘密情報 \(S\) を \(n\) 個の分散情報に符号化する暗号化アルゴリズムの一種。特に (k,n) しきい値法では \(n\) 個の分散情報のうち任意の \(k\) 個が揃えば元の秘密情報 \(S\) を再構築することができる (\(k\) 個に満たない場合は再構築することができない)。つまり分散情報の \(k-1\) 個までの盗難、あるいは \(n-k\) 個までの紛失・破損に耐えることができる。

\(n\) 個の鍵が全て揃わないと復号化できない暗号は全ての鍵を使用して暗号化すれば良い。ただしこの方法では 1 つでも鍵の紛失が発生すると秘密情報の復号化が不可能となる。また暗号化処理が \(n\) 回行われるため計算コストも高い。システムの参加者 (ユーザまたはノードなど) に復号化用の鍵を配布する場合、事故的な状況を想定して全参加者を揃えることが難しい事がある。

概要
1. (k, n) しきい値法
Shamir の秘密分散法
Blakley の秘密分散法
RSA 秘密分散共有
参考リンク

(k, n) しきい値法

\((k,n)\) しきい値法は秘密情報 \(S\) を以下の条件を満たす \(n\) 個の分散情報 \(S_1, S_2, \ldots, S_n\) に分割する。

任意の \(k\) 個以上の分散情報 \(S_i\) から容易に秘密情報 \(S\) を算出することができる。
任意の \(k-1\) 個以下の分散情報 \(S_i\) から秘密情報 \(S\) は完全に未定義となる (分散情報が 1 つもない状況での \(S\) の推定と同等の難しさを持つ)。つまり秘密情報 \(S\) は \(k\) 個未満の分散情報では再構築できない。

\(k=n\) のケースは元の秘密情報 \(S\) を復元するために全ての分散情報が必要であることを意味する。

Shamir の秘密分散法

Shamir の秘密分散法 [SMR] は \(k-1\) 次多項式において \(k\) 個の点が判明すれば式が決定することを利用する。秘密情報を \(S\) としたとき、\(a_0 = S\) とし残りの \(k-1\) 個の係数 \(a_1, \ldots, a_{k-1}\) を正の乱数整数から選択した多項式を定義する。\[ \begin{equation} f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_{k-1} x^{k-1} \pmod{p} \label{poly} \end{equation} \] ここで \(p\) は有限体とするための \(p \gt \max(S, k)\) となるような素数である。

最後に、多項式 (\(\ref{poly}\)) 上で \(i = 1, \ldots, n\) に対応する点を採取し、それらを分散情報 \(S_i = (i, f(i))\) として関係者に配布する。

結合 (復号) 過程では \(k\) 個の分散情報 \(S_i\) が与えられればラグランジュ補間を使用して秘密情報 \(a_0\) を容易に得ることができる。\(x\) が全て異なる \(k\) 個の点 \((x_1,y_1),\ldots,(x_k,y_k)\) を通る \(k-1\) 次多項式はラグランジュ補間公式より: \[ f(x) = \sum_{i=1}^k y_i \frac{\prod_{k \neq i}(x-x_k)}{\prod_{k \neq i}(x_i-x_k)} \] と表すことができる。従って秘密情報である切片 \(a_0\) は以下のように求めることができる。\[ \begin{equation} a_0 = f(0) = \sum_{i=1}^k y_i \frac{\prod_{k \neq i}(-x_k)}{\prod_{k \neq i}(x_i-x_k)} \label{lagrange-interpolation} \end{equation} \]

例1: \(k=3\) の秘密分散

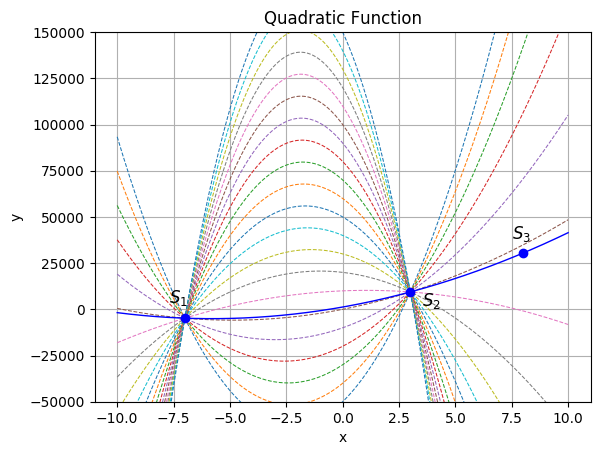
\(k=3\) のケースについて考えてみよう。目的とする多項式は、秘密情報を \(S = a_0\) とした 2 次関数である。\[ f(x) = a_0 + a_1 x + a_2 x^2 \] Fig 1. のように 2 次関数上の 2 点が分かったとしても関数を定めることはできないが、3 点が定まれば関数を定めることができる。これは 3 つの分散情報 \(\{S_1, S_2, S_3\}\) から元の秘密情報 \(S=a_0\) を復元することと等価である。

この 2 次関数から \((x, y)\) ペアを \(n\) 個採集した点を分散情報とすることで \(n\) 個のうち 3 個が揃えば復元できる鍵を作成することができる。

Undefined Quadratic Function — Fig 1. \(k=3\) 個以上の点が定まれば \(a_i\) を求めることができる。

例2: \(S=1234\) の秘密分散

例 1 の 2 次関数に具体的な値を適用してみよう。以下は秘密情報を \(S = 1234\) とし、\(a_1\), \(a_2\) は乱数から得た値である。\[ f(x) = 1234 + 2163x + 186x^2 \pmod{65521} \]

ここで位数の \(p=65521\) は \(p \gt \max(3,1234)\) を満たしデータサイズとして 16bit 幅に収まる最大の素数とした。条件を満たすだけであれば 1237 が最小の素数だが、それから秘密情報 1234 の推測が容易であることは明かだろう。大きな \(p\) を選択することで安全性を高めることができる。

各分散情報 \(\{S_1,S_2,\ldots,S_n\}\) は \(f(x)\) から任意の \(n\) 個の点を採集すれば良い。ここでは \(x=i\) とする。

\(k=3\) 個の分散情報が以下のように判明した場合: \[ \left\{ \begin{array}{rcl} S_1 & = & (1, 3583) \\ S_2 & = & (2, 6304) \\ S_3 & = & (3, 9397) \end{array} \right. \] これらの秘密分散を式 (\(\ref{lagrange-interpolation}\)) に当てはめると: \[ \begin{eqnarray} a_0 & = & 3583 \frac{-2 \times -3}{(1-2) \times (1-3)} + 6304 \frac{-1 \times -3}{(2-1) \times (2-3)} + 9397 \frac{-1 \times -2}{(3-1) \times (3-2)} \label{example1234} \pmod{65521}\\ & = & 1234 \nonumber \end{eqnarray} \] 秘密情報 \(S = 1234\) を復元することができる。式 (\(\ref{example1234}\)) の Wolfram|Alpha による解はこちら。

(k,n) しきい値法は参加者が不正な動作を行うと秘密情報を正しく復元することができないが、これに検証可能なスキーム (VSS; verifiable secret sharing scheme) を追加することができる。

Feldman (1987) の方法はディーラーが不正な分散情報を共有していないかを各参加者が検証できるように、素数位数 \(p\) を持つ有限巡回群 \(G_p\) とその生成元 \(g\) とする離散対数問題を使用する。

ディーラーは秘密情報の分散共有時に \(g^S, g^{a_1}, \ldots, g^{a_{k-1}} \in G_p\) を公開する (DLP 仮定の下では \(g\), \(p\), \(g^x \bmod p\) から \(x\) を求めることが困難であることに注意)。
参加者 \(P_i\) は自身に与えられた \(S_i = f(i) = S + a_1 i + \ldots + a_{k-1} i^{k-1}\) に対して \[ g^{S_i} = g^S \times (g^{a_1})^i \times \ldots \times (g^{a_{k-1}})^{i^{k-1}} \] が成り立つかを検証する。

この方法により秘密情報 \(S\) や各係数 \(a_i\)、\(P_i\) 以外の分散情報 \(S_{j \neq i}\) を明かすことなく \(S_i\) が正しいことを検証することができる。

Blakley の秘密分散法

Blakley の秘密分散 [BLK,SHM] はベクトル空間を使用した (k,n) しきい値スキーム。Shamir と同年に発表された。

同じ平面上の非平行線は必ずどこかの 1 点で交差し、同じ空間無いの非並行面は必ずどこかの 1 点で交差する。Blakley のスキームはこれを一般化し \(n\) 個の非並行な \((n-1)\) 次元超平面を各参加者の分散情報とし、秘密情報 \(S\) をそれらの交点とする。

RSA 公開鍵を使用して分散秘密鍵 \(sk_i\) を持つ全ての参加者が協力することで秘密情報を復元するスキーム。

鍵生成: ディーラーは RSA 秘密鍵 \(sk=d\) と公開鍵 \(pk=(e, n)\) を生成し公開鍵を公開する。そして、秘密鍵から \(d = (\sum_{i=1}^n d_i) \bmod \lambda(n)\) となるような \(n\) 個の分散秘密鍵 \(sk_i=d_i\) を生成し各参加者に配布する。
暗号化: 公開鍵 \(pk\) を使用して秘密情報 \(S\) を暗号化する。。
復号化: 参加者 \(P_i\) は \(S_i = e^{d_i} \bmod n\) を算出して他の参加者と共有する。全ての \(S_i\) から \(S = (\prod_{i=1}^n S_i) \bmod n\) を計算することができる。