ホワイトボックス暗号
概要
ホワイトボックス暗号 (white-box cryptography; WBC) は攻撃者が暗号プリミティブの実装やその実行プラットフォームに対して特権的アクセスを持つ状況においても暗号鍵そのものの漏洩 (つまり鍵復元) を防止することを目的とした難読化 (obfuscation) の手法である。安全性の完全な証明はされておらず、疑問の多い製品も販売されてはいるものの、強力な敵対者からの防衛に関してそれなりに有効なソフトウェアソリューションである [6]。
ホワイトボックス暗号は DES や AES といった一般的な対称鍵 (共有鍵) 暗号のブロックのラウンドの手順を難読化することによって行われる。これによって暗号化/復号化の機能に公開鍵暗号のような非対称性の特徴を与えている。公開鍵暗号と異なる点は、難読化した復号機構から鍵そのものを取り出すことが困難であるため、復号機構をハードウェア実装することで特定のハードウェアを持っているユーザのみが配信内容を復号化できるようなシステムを構築できる点である。
ホワイトボックス暗号の研究の背景には、このような暗号化されたコンテンツを販売・配信する DRM (digital rights management) への考慮がある。199x～200x 年にかけて、ユーザサイドで再生されるコンテンツのいくつかは BackupHDDVD
や FairUse4WM といったサイドチャネル攻撃を行う解読ツールを使って鍵そのものを復元・共有され誰でも販売内容を再生できた。ホワイトボックス暗号はそのような状況でもコンテンツを保護できるようにマルチメディアや DRM と同時期の 200x 年前半に盛んに研究された。昨今ではクラウド環境で安全に機密データを扱うための技術として再び注目を浴びている。
Table of Contents
暗号鍵 \(k\) による暗号化処理を \(E_k\) とし、平文 \(m\) の暗号文を \(E_k(m)\) とする。特にデータ保護を行っていなければ \(E_k\) はプレーンな (暗号論的に復元可能な) 鍵情報が含まれているため、攻撃者は \(E_k\) を解読すれば容易に暗号鍵 \(k\) を取り出すことができる。このような \(E_k\) は攻撃者の制御下に置かれた環境で実行されることを想定しないことは明らかである。
ホワイトボックス暗号は、たとえ攻撃者が暗号プリミティブの知識やその実行バイナリ、実行時のメモリやレジスタ状況を観測可能であったとしても、ある処理 \(P_k\) に含まれる鍵情報 \(k\) を復元することが現実的に困難となるように難読化した \(P'_k\) を生成する手法である。この変換を \(O\) とすると難読化とホワイトボックス暗号はそれぞれ式 (\(\ref{obfuscation}\)), (\(\ref{wbc}\)) のように表すことができる。\[ \begin{eqnarray} O & : & P_k & \to & P'_k \label{obfuscation} \\ \wb_p & : & k & \to & P'_k = O(P_k) \label{wbc} \end{eqnarray} \] 難読化前後の処理は等価 \(P_k \equiv O(P_k)\) でなければならないのは明らかである。一般に、このような難読化によってプログラムのサイズは大きく増加し、処理も大幅に遅くなる。
\(P'_k\) から鍵を抽出する代わりに \(P'_k\) の実装自体をコピーして使用することをコードリフティング (code lifting) と呼ぶ。ホワイトボックス暗号は解読した暗号鍵が再配布され悪意をもって使用されることを防ぐことを意図しているためコードリフティングまで考慮していないが、例えば難読化 \(O\) の中に状況依存の外部エンコーディング (例えばランダムに対消滅する処理 \(F\) と \(F^{-1}\) のペア) を埋め込むことで (完全ではないが) 特定のコンテキストでのみ利用可能な難読化を構築するといった対策が考えられる。
脅威モデル
完全なセキュリティの暗号技術は存在しないという仮定のもとで、ある暗号技術がどのようなセキュリティを提供するかはその暗号技術がどのような驚異モデル (threat model) に対処できるかを示すことによって行われる。脅威モデルとは 1) 攻撃者のゴールは何か、2) 攻撃者が利用できるリソースは何かの 2 点の定義である。
ブラックボックス暗号
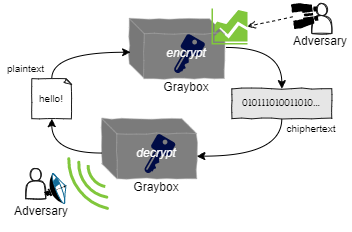
攻撃者が暗号プリミティブの知識を持ち暗号化/復号化処理の入出力のみを観測できる (つまり平文や暗号文を観測可能だが内部状態は分らない) という脅威モデルに基づく暗号をブラックボックス暗号 (black-box cryptography) と呼ぶ (Fig 1)。DES や AES のような従来の暗号プリミティブはブラックボックス攻撃からデータや鍵を保護するように設計されている。
ブラックボックス暗号はアルゴリズム自体が公知であっても鍵情報の機密性が保たれている限り安全であるというケルクホフスの原理に基づいた考えである。
しかし、スマートカードや HSM (hardware security module) のように攻撃者がハードウェアを制御下に置いている状況では暗号化/復号化の処理時間や消費電力、発生する電磁波といったサイドチャネルの物理的な観測によってブラックボックス内の鍵の推測を試みることができる。このため昨今のクラウド環境のようにハードウェアを他人に委ねている状況では鍵情報を安全に保護できていると断言することは難しいという見方もある。このような脅威モデルに対する暗号をグレイボックス暗号 (gray-box cryptography) と呼ぶ (Fig 2)。
ホワイトボックス暗号
ペネトレーションテストのような攻撃者が OS やソフトウェア実装に無制限にアクセスできる脅威モデルでは、サイドチャネル攻撃に加えて、暗号化/復号化処理を自由に呼び出したり、実行コードを改変して秘匿情報の可視化を試みたり、また逆アセンブルしてハードコードされたデータを取り出すことを想定する。そのような状況においても暗号化/復号化のための鍵やデータを漏洩しない暗号をホワイトボックス暗号 (white-box cryptography) と呼ぶ。
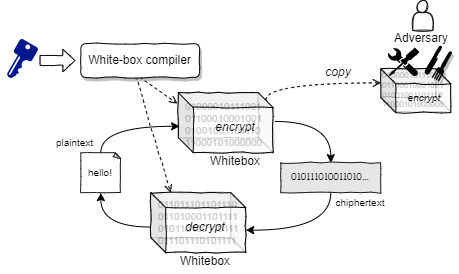
一般にホワイトボックス暗号は暗号化/復号化のような機能だけを提供して鍵情報そのものを含まず、機能を解読しても鍵を復元することが現実的に困難であるという不可逆性を持つ。
エントロピー攻撃
暗号鍵と暗号化/復号化処理をビットの並びとして比較したとき、暗号鍵は非常に大きな定義域からランダムに選択されるためエントロピーが高く、一方でコンパイル済みのバイナリは限られた数の命令セットの中から選択された命令の並びであるためエントロピーが低い。Fig 4 は鍵を含むプログラムのビットの並びをピクセルに置き換えた画像である。データ保護されていない実行ファイルやメモリ上の並びから暗号鍵の位置を推測することは困難ではない。
エントロピー攻撃に対して鍵のデータを分割して保存したり、同時にメモリ上に乗らないような手法が提案が行われたが、プログラムの動的解析 (実行時解析) を使ってメモリの位置を追跡することで元の鍵を復元することが難しくないことが分かった。結果的に 199x 年代の終わりにはプログラムに埋め込んだ鍵を秘匿化することは不可能だろうと考えられるようになった [2]。
キーホワイトニング攻撃
AES などの反復ブロック暗号は key whitening と呼ばれる \(P(S(x)) \oplus k\) 処理を行っている。S-box に相当する処理 \(S\) は公知であるため、攻撃者がプログラム内から処理 \(P\) の位置を見つけだすことは困難ではない。ここで攻撃者が \(P\) のすべての出力が 0 となるように書き換えた場合、\(P(S(x)) \oplus k = k\) となり暗号鍵がそのまま出力されることになる。
コード難読化
難読化 (obfuscation) はプログラム \(P\) の動作を変えずにランダム性を加えた改変 \(O(P) \equiv P\) を行うことである。人がプログラムの意図を読み解くことを困難にすることで、プログラムの動作アルゴリズムを秘匿したり、カスタマイズされることを防ぐことを目的としている。一般的に難読化 \(O\) は以下の特徴を満たす必要がある。
- 機能性: あるプログラム \(P\) とそれを難読化したプログラム \(O(P)\) は機能的に同等である。
- 実用性: \(O(P)\) のサイズやパフォーマンスが現実的である (一般に難読化によってプログラムのサイズや実行時間は大きく増加する)。
- 仮想ブラックボックス (virtual black-box): 難読化されたコードからプログラムに関するいかなる秘密ビットも明らかにされない。
任意のプログラムを難読化できる \(O\) を構築することが不可能であることが [4] によって示されている。ただし難読化の可能性そのものを否定するものではなく、鍵情報の秘匿に関してはランダムオラクルモデル、近似多重写像 (approximate multi-linear maps)、トラップドアなどを使ったいくつかの実用的なメカニズムが提案がされている。
鍵情報は実装全体に分散している必要があり、攻撃者は実装全体を分析しなければならない。エントロピー攻撃やキーホワイトニング攻撃のような局所的な解析による鍵の復元を防ぐために構成要素をランダム化する必要がある。
Chow ら (2002) による最初のホワイトボックス実装は暗号化処理が \(E_k(x) = T_k(x)\) となるような巨大なルックアップテーブル \(T_k: x \to y\) を構築することだった。ルックアップテーブルはランダム化されており、にはランダム対消滅エンコード (random annihilating encoding) を行うことで
メモリ上の読み取りは
参考文献
- A.Shamir, N.V.Someren. Playing hide and seek with stored keys, Lecture Notes in Computer Science, 1998.
- Brecht Wyseur. White-Box Cryptography: hiding keys in software, MISC magazine, Apr 2012.
- Brecht Wyseur. White-Box Cryptography, , Mar 2009.
- B.Barak, O.Goldreich, R.Impagliazzo, S.Rudich, A.Sahai, S.Vadhan, K.Yang. On the (Im)possibility of obfuscating programs, In CRYPTO 2001, pages 1–18. Springer, 2001.
- Matthieu Rivain (2017) White-Box Cryptography
- David Wong. Real-World Cryptography. Manning (2021)