セキュリティ
\(\newcommand{\wb}{W\!B}\)

論文翻訳: WHITE-BOX CRYPTOGRAPHY: HIDING KEYS IN SOFTWARE

Takami Torao 2012年の論文 #WBC #ホワイトボックス暗号
  • このエントリーをはてなブックマークに追加

著者: Brecht Wyseur Brecht.wyseur@nagra.com, NAGRA Kudelski Group, Switzerland

Table of Contents

  1. 1. 導入
  2. 2. ホワイトボックス暗号
    1. 2.1 ホワイトボックス実装
    2. 2.2 ホワイトボックス暗号解析
    3. 2.3 理論的アプローチ
  3. 3. ホワイトボックス暗号の実用化
    1. 3.1 コードリフティング
    2. 3.2 ソフトウェアフィンガープリント
  4. 4. 結論
  5. ACKNOWLEDGEMENTS
  6. BIBLIOGRAPHY
  7. 翻訳抄

1. 導入

暗号技術の当初の目的は通信チャネルを盗聴から守るためのアルゴリズムとプロトコルを設計することだった。これは過去 30 年間の現代暗号の主な活動であり、(AES, (T)DES, RSA, ECC など) 多くの優れた暗号やプロトコルが生み出されてきた。これらのスキームではエンドポイントが信頼されていると仮定されており (ブラックボックス)、攻撃者はアルゴリズムの入力/出力にのみアクセスできる。このようなモデルに準拠するにはアルゴリズムを安全な環境で実行する必要がある。この分野では改良された特殊用途の暗号 (軽量ブロック暗号、認証スキーム、準同型公開鍵アルゴリズムなど) や、その暗号解読に関する研究が盛んにおなわれている。しかし産業の観点から見ると主な問題は実用的な配備にある。誤ったコンテキストで導入されたプロトコル、不適切に実装されたアルゴリズム、または不適切なパラメータは攻撃者の侵入口となる可能性がある。暗号を実際に配備すること自体が課題となっている。

この問題はブラックボックス攻撃モデルが満たされなくなるとさらに悪化する。この 10 年間で暗号アルゴリズムの実行中に観測される実行タイミング、電磁波、消費電力などのサイドチャネル情報を組み込んだ新しい暗号解読技術が次々と登場している。このサイドチャネル情報を秘密鍵の操作と非相関に行うことは困難であるため、このようなサイドチャネル攻撃を軽減することは難問である。さらに、プラットフォームにはサイズや性能の要件が課されていることが多く、保護技術の導入が困難になっている。

最近では、オープンなデバイス (セキュアな要素を使用していない PC やタブレット/スマートフォンなど) で実行されるアプリケーションに暗号が配備されるといったさらに悪い攻撃モデルに遭遇することもある。ここではこれを "ホワイトボックス攻撃" (white-box attack) と呼ぶ。このような状況で "ホワイトボックス攻撃者" は暗号アルゴリズムのソフトウェア実装に完全にアクセスすることができる。すなはち、攻撃者はバイナリを完全に可視化して変更することができ、実行プラットフォーム (CPU コール、メモリやレジスターなど) を完全に制御することができる。そのため実装そのものが唯一の防衛策となる。

ホワイトボックス暗号で対処する課題は、ホワイトボックス攻撃を受けても暗号化資産 (cryptographic assets) が安全に保たれるようにソフトウェアに暗号アルゴリズムを実装することである。

このようなホワイトボックス攻撃に対抗するソフトウェア実装はホワイトボックス実装と呼ばれる。ホワイトボックス実装は DRM アプリケーションなど、資産を保護するために暗号鍵を使用するアプリケーションの基礎となるものである。このようなケースでは、ソフトウェアのユーザはアプリケーションをリバースエンジニアリングして秘密鍵を抽出するインセンティブを持っている。同様の攻撃は、例えばバンキングアプリケーションがマルウェアに感染したデバイス上で実行された場合や、他のユーザが特権を持つマルチユーザシステム上で実行された場合など、アプリケーションのユーザにインセンティブがない場合でも発生する可能性がある。このような状況で OpenSSL などの標準的な暗号ライブラリを使用して暗号処理を行ったり、暗号鍵をプレーンメモリに保存すると、どんなに強力な暗号プリミティブを使用していても秘密鍵は簡単に公開されてしまう。

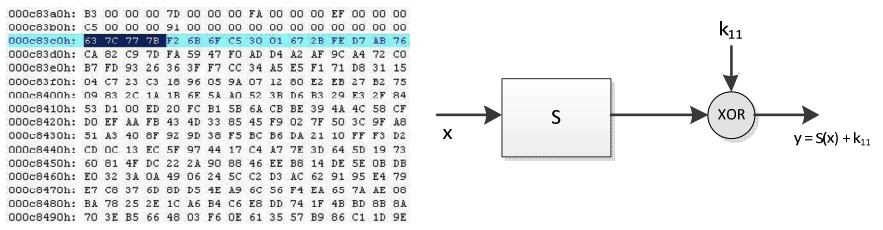
このようなホワイトボックス攻撃を説明するために Kerins and Kursawe [Kerins06] の ”キーホワイトニング攻撃" (key whitening attack) を紹介する。この攻撃は OpenSSL 実装を含むほとんどの AES 実装に展開することができる。AES は操作の最終ステップにキーホワイトニング操作 ─ 暗号の最終ラウンドを消滅 (annihilate) から保護するために最終ラウンドの鍵を使って追加される操作を配置していることに注意 (Figure 1 参照)。後ろから二番目の操作はテーブルルックアップ操作である。この暗号スキームは公開されているためテーブルルックアップの定義は公知でありホワイトボックス攻撃者もアクセス可能である。実際、シンプルな 16 進数エディタを使ってこれらのルックアップテーブルをバイナリ上に配置しセロに変更することができる。その結果、後ろから二番目の演算の出力はゼロになり、実装を実行すると最終ラウンドの鍵が出力され、そこから元の AES 鍵を簡単に導き出すことができる。

Figure 1 - キーホワイトニング攻撃

この記事ではホワイトボックス暗号の幅広い領域を紹介する。最初に発表されたホワイトボックス実装を紹介し、主要な暗号解読結果を説明する。結果として提起された存在証明 (existence proof) や境界などの存在問題はホワイトボックス暗号の研究においてより理論的なサイドトラックで扱われるが、このトピックでは簡単にしか触れない。最後に、ホワイトボックス実装が実際にどのように攻撃されているか、現実的な問題を軽減するためにどのような追加のセキュリティメカニズムを導入できるのか、そして今後どのような課題があるのかといった、より実践的な側面について説明する。

2. ホワイトボックス暗号

最初のホワイトボックス暗号は Chow ら [Chow02DES] が固定鍵ホワイトボックス DES 実装を取り上げて発表した。ここでの課題はブロック暗号の実装に DES の共通鍵をハードコーディングすることである。主なアイディアは、固定鍵 (データの形式だがコードの形式でもある) とランダムデータ (コンパイル時にインスタンス化される) の両方を、元の鍵を導き出すことが困難な構成で埋め込むことだった。

暗号技術の主要な設計原理の一つに、暗号システムは鍵を除くシステムの全てが公知であっても安全でなければならないというケルクホフの原理 (Kerckhoffs’ principle) がある。ホワイトボックス暗号は同様の公的な監視に耐えることを目的としている。攻撃者は実装にフルアクセスできるだけでなく、どのアルゴリズムが実装され、どのようなホワイトボックス保護技術が適用されているかも知っている。セキュリティは秘密鍵とランダムデータの機密性に依存している。これは、攻撃者が秘密のアルゴリズムは IP に敏感なコードを開示できないようにアプリケーションコードのリバースエンジニアリングを防ぐことを目的としたコード難読化でしばしば考えられる "隠すことによるセキュリティ" アプローチとは対照的である。

2.1 ホワイトボックス実装

最初のホワイトボックス実装は 2002 年に Chow ら [Chow02DES, Chow02AES] によって DES と AES のそれぞれについて発表された。彼らのホワイトボックス技術は暗号を鍵に依存する一連のルックアップテーブルに変換する (Figure 2 (a) 参照)。秘密鍵はルックアップテーブルにハードコードされており、ランダム化技法を適用することで保護されている。この方法では、ランダム対消滅エンコーディングをルックアップテーブルに挿入してルックアップテーブルとその間のデータフローをランダム化することで実装全体のセマンティクス機能を維持している。これは Figure 2 (b) に示されており、F と G はそれぞれ A, B と B, C 間に挿入されるランダムエンコーディングである。全体的な機能 (入力 A - 出力 C) は変わらない。

Figure 2. Chow らのホワイトボックス実装

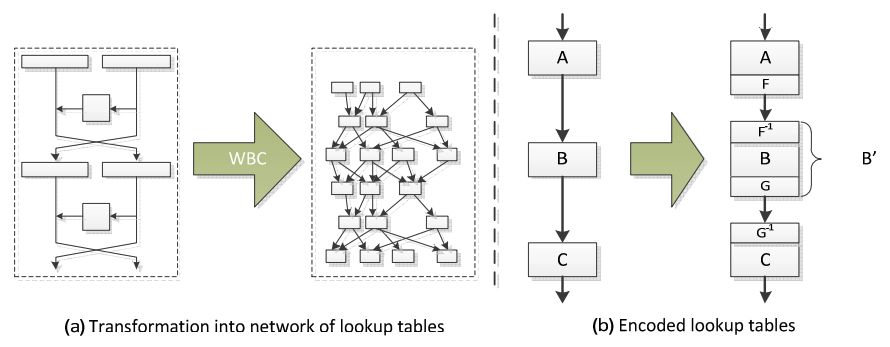
暗号をルックアップテーブルのネットワークに変換する手法を他の SPN (substitution-permutation network) 構造ブロック暗号に拡張することは簡単である。非常に高いレベルから、手順は次のようになる:

  1. S-box 演算とラウンドキーを含む演算が互いに隣接するように暗号を再編成し、例えば \(T_k(x) = S(x) + k\) のように S-box に秘密鍵をハードコーディングする。
  2. アフィングロック暗号のそうに対消滅するアフィン演算を挿入する。こうすることで S-box の順序を変えたり、(通常は可能な限り効率的になるように設計されている) アフィン演算のスパース性を下げることができる (Chow らの論文ではこれを "mixing bijections" の導入と呼んでいる)。
  3. すべてのアフィン演算を一連のルックアップテーブルに分解する。これにより XOR 演算もルックアップテーブルとして実装することもできる。
  4. ルックアップテーブルの配列にランダム対消滅エンコーディングを挿入する。

これは非常にアドホックな暗号プリミティブの実装方法であり、そのセキュリティを定量化することは困難である。導かれる唯一のセキュリティステートメントは "局所的な安全性" であり、B が全単射で F と G がランダムに選択されているなら B' は何の情報も漏洩しない。実際、B' が与えられた場合、入力と出力が同等のビット数を持つ任意の全単射 B が候補となる。なぜなら B' = G.B.F-1 となるような F, G のペアが常に存在するためである。したがって、攻撃者は実装の他のコンポーネントも分析する必要がある。最終的に攻撃者はあまりにも多くの変数を考慮しなければならず、攻撃が不可能になることを目的としている。残念ながらこのステートメントを裏付けるセキュリティ証明はない。次のセクションでは Chow らのアプローチがどのようにして破られるかを説明する。

XOR 演算子などの効率的な演算がルックアップテーブルに変換されるため、パフォーマンスとサイズのオーバーヘッドが大きくなる。

実装 サイズ 参考
WB-AES [Chow02AES] 770 kBytes 14.5 kBytes (OpenSSL 1.0)
WB-DES [Chow02DES] 4.5 MBytes 8.25 kBytes (OpenSSL 1.0)
WB-DES [Link05] 2.3 MBytes

2.2 ホワイトボックス暗号解析

ホワイトボックス DES 実装 [Chow02DES] は安全でないことが最初に示されたものだった。その脆弱性は主に DES の Feistel 構造に起因するもので、ルックアップテーブル表現で区別することができる。最初のホワイトボックス暗号解析技術は fault propagation correlation [Jacob02] や guess & determine attacks [Link05] などのサイドチャネル攻撃にその期限を見出すことができる。ただしこれらの技術にはいくつかの仮定を置いており容易に緩和することができる [Link05]。Wyseur ら [Wyseur07] や Goubin ら [Goubin07] による truncated differential cryptanalysis でホワイトボックス DES 実装が完全に破られたのは 2007 年になってからだった。

ホワイトボックス AES 実装は Billet ら [Bil04] によって代数的な暗号解読技術を用いて破られている。ここで提示された代数的手法はルックアップテーブルのランダム化という戦略を直接ターゲットとしているため非常に協力であることが示されている。詳細は省くが、攻撃の考え方は以下の通りである:

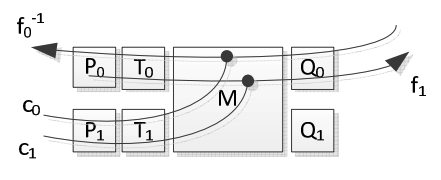
  1. 基礎となる AES 実装の 1 つの (エンコードされた) ラウンドを表すルックアップテーブルのセットを分離する。展開される変換は (秘密鍵と導入されたランダム性まで) 既知であるためこれは簡単である。Figure 3 はこのようなラウンドの構成を示しており、P と Q は内部エンコーディング、Ti はハードコードされた鍵を持つ S-box、M は暗号の線形部分 (MixColumns 演算など) を表している。
  2. 関数 fi ラウンドの入力側のバイトと出力側のバイトとの間の全単射関数として定義する。他のバイトへの入力は一定だが fi ごとに異なる。
  3. これらの fi は全単射で 8-bit で動作するするため容易に反転することができる。このため合成関数 hij = fj.fi-1 を計算することができる。
  4. これらの関数 hij から Q0 の非線形成分を導き出すことができる。これは、関数 hij が Q0 と定数 ci, cj にのみ依存し P0 と T0 には依存しないためである。
  5. Q0 の情報は次のラウンドの P0 につながっている (これらは対消滅するエンコーディングであるため互いに逆である)。したがって手順 1〜4 を数ラウンドに渡って繰り返すと線形エンコーディングでのみ保護された AES 実装となる。あとは残りの方程式を説いて埋め込まれた秘密鍵を導出することができる。
Figure 3 - ホワイトボックス AES 実装の 1 ラウンド分の解析結果

Michiels ら [Mich08] はこの代数的暗号解析技術が AES と同様の特性を持つ任意の暗号 (すなはち MDS 行列を使用する SPN 暗号) に展開できることを示した。実際彼らは、ホワイトボックス攻撃に対して脆弱となるのはまさにブラックボックスセキュリティの観点から選択した特性であることを示している。[Wyseur09] では代数的攻撃を使ってルックアップベースのホワイトボックス全体を打ち破る方法を示した。損失のあるルックアップテーブル (ルックアップテーブルベースのホワイトボックス実装では避けられない) は悪用できる情報を漏洩する。

代数的暗号解析技術はルックアップテーブル戦略を超えた新しい構造の設計に繋がり、ランダム化された代数方程式を用いた実装への方向性 [Bil03] や、代数的攻撃を実装できる代数構造を打ち破る摂動の導入 [Bri06wbc] をもたらした。Billet と Gilbert による実装 [Bil03] は基礎となるプリミティブの暗号解読結果が破られた。この問題を解決する試みは Ding [Ding04] に触発され、代数的構造を "破壊" する摂動関数を挿入するようになった。これは改良された追跡可能なブロック暗号スキーム [Bri06trace] につながり、最終的にはホワイトボックス AES 実装に適用された [Bri06wbc]。しかし改良されたこれらの新しい構造でさえ De Mulder ら [Dem10] によって安全でないことが示されている。

これまでに発表されたすべての新しい構造にもかかわらず、ホワイトボックス暗号の安全性は非常に不明確である。発表されたほとんどすべての構造は学術的に発表された暗号解析の論文で安全でないことが示されている。わずかに "壊れていない" 構造が残っているが、それは既存の構造に少し手を加えただけのもので、したがって既存の攻撃は殆ど労力をかけずに適用できる。

"学術的な" ホワイトボックス暗号の現状を考慮すると以下のような疑問が残る:

  • "強力な" ホワイトボックス実装は存在するのか、また、どのようなホワイトボックスセキュリティが実現可能か?
  • 現実のシナリオにおいて攻撃を悪用することはどれほど難しいか?

これらの質問については次のセクションで説明する。

2.3 理論的アプローチ

ホワイトボックス暗号はソフトウェア実装の保護を目的としているため、しばしばコードの難読化と結び付けられる。そのどちらも実現可能性と論理的根拠の欠如については同等の懐疑的な意見がある。コード難読化の理論的な研究は Barak ら [Barak01] の重要な論文で勢いを増した。Barak らは汎用難読化装置、すなはち任意のプログラムを保護できる難読化装置を構築することは不可能であることを示した。Barak らはソフトウェアがその機能を維持したまま常にコピーできるという事実を利用して難読化できない関数群を構築した。しかしこの結果は安全なコード難読化装置の存在を廃城するものではない。Wee [Wee05] は実際に認証機能を駆逐するために使うことができる、ポイントファンクション向けの証明可能なセキュア難読化装置を発表した。

同様の論理的アプローチはホワイトボックス暗号についても [Sax09] で考案されている。コード難読化とホワイトボックス暗号の主な違いは、後者はセキュリティ概念に基づいてセキュリティを検証する必要があるということである。セキュリティ概念とは暗号化スキームのセキュリティを形式的に記述したものである。例えば、攻撃者が特定の暗号文から平文を算出できない場合は CPA セキュア、秘密鍵を復元できない場合は KR セキュアというスキームが定義されている。

ホワイトボックス暗号はより現実的なものを反映しているため、それに応じて定義することが理にかなっている。実際、アプリケーションに埋め込まれた秘密鍵の抜き取りを防止するだけでは不十分である。例えばスマートカードに搭載された AES 暗号と同等の機能をソフトウェアで実装するためには、埋め込まれた鍵を抜き取られないだけではなく、反転が困難でなければならない。[Sax09] において Saxena と Wyseur はいくつかのセキュリティ概念はソフトウェアでは満たせないことを示し (IND-CCS2)、IND-CPA セキュリティ概念に関して証明可能なセキュア構造を提示した。

論理的にはホワイトボックス暗号が対称暗号と非対称暗号の間の架け橋と見なせることが示されている。プライベートな操作は対称鍵でインスタンス化されたブロック暗号によって効率的に実行され、パブリックな操作は同じ対称鍵をコードに埋め込んだ暗号化関数のホワイトボックス実装であるような、新しいタイプの公開スキームを構築することができる。これは単に秘密鍵の抽出を保護するよりも実現が難しいことに注意。例えば暗号解析の結果を考慮しない場合、各ラウンドは 4 つの並列 32-bit から 32-bit 演算として記述できるため、元のホワイトボックス AES 実装は間t何に "反転" させることができる。

3. ホワイトボックス暗号の実用化

Microsoft, Apple, Irdeto, NAGRA, Sony, Arxan など、多くの企業がホワイトボックス技術の導入を発表したり、特許を取得したり、またそのような技術を導入したことを示したりしている。これはmでは秘密鍵がハードコーディングされている固定鍵のホワイトボックス実装について説明してきた。しかし実施兄は、動的なホワイトボックス実装のほうが適している。これは、呼ばれたときにだけ鍵がインスタンス化される実装である。もちろんそのような場合、元の鍵ではなく (それでは簡単に公開されてしまう)、保護されたバージョンの鍵が提示される。動的ホワイトボックス実装では、この鍵に関する情報が公開されないように保護バージョンの鍵を解析して暗号化/復号化操作を実行する。

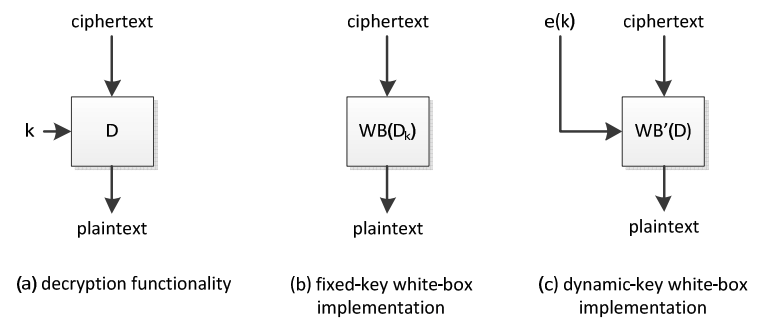
ホワイトボックス暗号の主な懸念はパフォーマンスとサイズの問題、そしてセキュリティである。パフォーマンスの問題はモバイルシステムなどの高スループットや制約のあるユースケースでのホワイトボックス暗号の利用を制限する。この問題はハードウェアアクセラレータを有効利用する専用のホワイトボックス実装を使用して解決できる。

セキュリティに関しては、これまでに発表された暗号解読結果にも関わらず、我々が知る限り実際の製品で鍵復元攻撃を受けたホワイトボックス実装は存在しない。これは理論と実践の間に明確なギャップがあることを示しており、したがって "弱い" ホワイトボックス実装であっても、ある程度までその目的を果たすことができるということである。このような攻撃を実際に展開することがどれほど難しいかを知るために、我々は "弱い" ホワイトボックス実装に関するいくつかの公開チャレンジを行った。その結果、2 つの独立した鍵復元結果が得られた。これらの攻撃の結論は、実際にホワイトボックス実装を破壊することは、単独で非常に時間のかかる作業であるということである。これらの攻撃はホワイトボックス実装の構造や基礎となる暗号の特性に大きく依存する。したがって、広く適用可能な攻撃を展開することは困難であり、それらを破るための自動ツールは存在しない。

3.1 コードリフティング

ホワイトボックス実装が実際に被る主な問題は "コードリフティング" (code lifting) である。このような攻撃では攻撃者は実装から秘密鍵を抽出しようとはせず、実際に何度か見たケースでは代わりにアプリケーション全体をあたかも大きな鍵であるかのように利用する。セキュリティライブラリをリバースエンジニアリングされていないが、その代わりにその復号化機能を直接呼び出して機能を悪用する。

コードリフティングはホワイトボックス実装の境界を押し上げることで緩和することができる。これは、元のスキームに外部エンコーディングを適用し、アプリケーション内の他の場所に対消滅エンコーディングを含めることで実現できる。例えば対消滅エンコーディングは復号化操作を呼び出す関数に組み込むことができる。その結果、攻撃者が G と F の知識を持たなければ意図した文脈以外で復号化操作を使用することはできない (G.Dk.F-1) が実装される。次に難読化技術やプロセス分離などを安全な環境に組み込むことで、これらの関数 G および F が呼び出し関数から抽出されないようにする。その結果、暗号操作を安全なコンポーネントに関連付ける方法としてノードロックを行うことができる。これは予防的ソフトウェア保護手法の一例である。

3.2 ソフトウェアフィンガープリント

もう一つの方向性は (鍵を埋め込んだ) コードを共有しているユーザを検出できるようなリアクティブな戦略を展開することである。[Mich07] において Michiels と Gorissen はホワイトボックスの実装にフィンガープリントを挿入する手法を発表した。アイディアの主旨は、最終ルックアップテーブルに任意の定義済み値を含むように内部の対称滅エンコーディングを選択するという観察である。この値はソフトウェアを識別したり暗号鍵に著作権を導入するフィンガープリントとして使用することができる。同じ方法でソフトウェアの耐タンパー性を実現することができる。結果として得られるルックアップテーブルにバイトコードやアセンブリ命令を表す値が含まれている場合、この表現を変更するとホワイトボックスのルックアップテーブルが変更されてレンダリングされる。その結果、基礎となる暗号の機能が使用できなくなる。そのためソフトウェアには二重の表現が存在することになる。しかしながら、このアプローチのセキュリティには疑問がある ─ まず、これはすでに疑問だがホワイトボックス実装のセキュリティに依存すること。次に、攻撃者はフィンガープリントを破壊するために追加の内部エンコーディングを挿入したり、コードの実行の基盤となるホワイトボックス実装の実行を区別するクローニング攻撃を手なきすることができるため、このようなアプローチは簡単に破られる。

より強力なリアクティブ戦略は、本質的に追跡可能なホワイトボックス実装を作成した Billet と Gilbert [Bil03] によって提示された。つまり、彼らは新しいブロック暗号の構造を提示し、そこからいくつかのインスタンスを生成することができる。各インスタンスは機能的に同等だが、コードを検査すれば識別が可能である。しかし残念ながらこのブロック暗号を構築するための基本的な構成要素が破られてしまった。Bringer ら [Bri06trace] は摂動を導入するというアイディアに基づいて追跡可能なブロック暗号を強化した。

4. 結論

ホワイトボックス暗号はあらゆる健全なソフトウェアセキュリティ戦略において必要な構成要素であり、敵対的な実行プラットフォーム上で実行されるアプリケーションの暗号プリミティブを保護するための基礎となる。最初のホワイトボックス技術は 2002 年に発表され、DES 暗号と AES 暗号の実装が行われた。それ以来、ホワイトボックス暗号は勢いを増し、いくつかの暗号解読結果や新しい構造を目の当たりにして論理的な基礎が確立されてきた。

最近ではホワイトボックス暗号が主に DRM アプリケーションなどの実世界のアプリケーションで使用されてる。学術的な攻撃が発表されているが、我々が知る限り商用のホワイトボックス実装に対する攻撃は見られていない。むしろ、攻撃者はシステムの他の部分に注目し、暗号機能を攻撃することなく利用している。ホワイトボックスの実装をアプリケーションにロックする子男でコードリフティング攻撃を軽減したり、トレーサビリティなどの他のセキュリティ機能をホワイトボックス実装に搭載することができる。

ACKNOWLEDGEMENTS

The original version of this article has been written in English, and can be retrieved at www.whiteboxcrypto.com. We would like to thank Jean-Bernard Fischer for his effort to translate this article into French.

BIBLIOGRAPHY

  1. [Barak01] Boaz Barak, Oded Goldreich, Rusell Impagliazzo, Steven Rudich, Amit Sahai, Salil Vadhan, and Ke Yang. On the (Im)possibility of Obfuscating Programs. In Advances in Cryptology - CRYPTO 2001, volume 2139 of Lecture Notes in Computer Science, pages 1–18. Springer-Verlag, 2001.
  2. [Bil03] Olivier Billet and Henri Gilbert. A Traceable Block Cipher. In Advances in Cryptology - ASIACRYPT 2003, volume 2894 of Lecture Notes in Computer Science, pages 331–346. SpringerVerlag, 2003.
  3. [Bil04] Olivier Billet, Henri Gilbert, and Charaf Ech-Chatbi. Cryptanalysis of a White Box AES Implementation. In Proceedings of the 11th International Workshop on Selected Areas in Cryptography (SAC 2004), volume 3357 of Lecture Notes in Computer Science, pages 227–240. Springer-Verlag, 2004.
  4. [Bri06trace] Julien Bringer, HervèF Chabanne, and Emmanuelle Dottax. Perturbing and Protecting a Traceable Block Cipher. In Proceedings of the 10th Communications and Multimedia Security (CMS 2006), volume 4237 of Lecture Notes in Computer Science, pages 109–119. SpringerVerlag, 2006.
  5. [Bri06wbc] Julien Bringer, Herve Chabanne, and Emmanuelle Dottax. White box cryptography: Another attempt. Cryptology ePrint Archive, Report 2006/468, 2006.
  6. [Chow02DES] Stanley Chow, Philip A. Eisen, Harold Johnson, and Paul C. van Oorschot. A white-box DES implementation for DRM applications. In Proceedings of the ACM Workshop on Security and Privacy in Digital Rights Management (DRM 2002), volume 2696 of Lecture Notes in Computer Science, pages 1–15. Springer, 2002.
  7. [Chow02AES] Stanley Chow, Philip A. Eisen, Harold Johnson, and Paul C. van Oorschot. White-Box Cryptography and an AES Implementation. In Proceedings of the 9th International Workshop on Selected Areas in Cryptography (SAC 2002), volume 2595 of Lecture Notes in Computer Science, pages 250–270. Springer, 2002.
  8. [Dem10] Yoni De Mulder, Brecht Wyseur, and Bart Preneel, "Cryptanalysis of a Perturbated White-box AES Implementation," In Progress in Cryptology - INDOCRYPT 2010,Lecture Notes in Computer Science 6498, K. Chand Gupta, and G. Gong (eds.), Springer-Verlag, pp. 292-310, 2010.
  9. [Ding04] Jintai Ding. A New Variant of the Matsumoto-Imai Cryptosystem through Perturbation. In Proceedings of the 7th International Workshop on Theory and Practice in Public Key Cryptography (PKC 2004), volume 2947 of Lecture Notes in Computer Science, pages 305–318. Springer-Verlag, 2004.
  10. [Goubin07] Louis Goubin, Jean-Michel Masereel, and Micha¨el Quisquater. Cryptanalysis of White Box DES Implementations. In Proceedings of the 14th International Workshop on Selected Areas in Cryptography (SAC 2007), volume 4876 of Lecture Notes in Computer Science, pages 278–295. Springer-Verlag, 2007.
  11. [Jacob02] Matthias Jacob, Dan Boneh, and Edward W. Felten. Attacking an Obfuscated Cipher by Injecting Faults. In Proceedings of the ACM Workshop on Security and Privacy in Digital Rights Management (DRM 2002), volume 2696 of Lecture Notes in Computer Science, pages 16–31. Springer, 2002.
  12. [Kerins06] Tim Kerins and Klaus Kursawe. A cautionary note on weak implementations of block ciphers. In 1st Benelux Workshop on Information and System Security (WISSec 2006), page 12, Antwerp, BE, 2006.
  13. [Link05] Hamilton E. Link and William D. Neumann. Clarifying Obfuscation: Improving the Security of White-Box DES. In Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC 2005), volume 1, pages 679–684, Washington, DC, USA, 2005. IEEE Computer Society.
  14. [Mich07] Wil Michiels and Paul Gorissen. Mechanism for software tamper resistance: an application of white-box cryptography. In Proceedings of 7th ACM Workshop on Digital Rights Management (DRM 2007), pages 82–89. ACM Press, 2007.
  15. [Mich08] Wil Michiels, Paul Gorissen, and Henk D.L. Hollmann. Cryptanalysis of a Generic Class of WhiteBox Implementations. In Proceedings of the 15th International Workshop on Selected Areas in Cryptography (SAC 2008), Lecture Notes in Computer Science. Springer-Verlag, 2008.
  16. [Sax09] A. Saxena, Brecht Wyseur, and Bart. Preneel, "Towards Security Notions for White-Box Cryptography," In Information Security - 12th International Conference, ISC 2009, Lecture Notes in Computer Science 5735, C. A. Ardagna, F. Martinelli, P. Samarati, and M. Yung (eds.), Springer-Verlag, 10 pages, 2009.
  17. [Wee05] Hoeteck Wee. On Obfuscating Point Functions. In Proceedings of the 37th ACM Symposium on Theory of Computing (STOC 2005), pages 523–532, New York, NY, USA, 2005. ACM Press.
  18. [Wyseur07] Brecht Wyseur, Wil Michiels, Paul Gorissen, and Bart Preneel. Cryptanalysis of White-Box DES Implementations with Arbitrary External Encodings. In Proceedings of the 14th International Workshop on Selected Areas in Cryptography (SAC 2007), volume 4876 of Lecture Notes in Computer Science, pages 264–277. Springer-Verlag, 2007.
  19. [Wyseur09] Brecht Wyseur, "White-Box Cryptography," PhD thesis, Katholieke Universiteit Leuven, Bart Preneel (promotor), 169+32 pages, 2009.

翻訳抄

ホワイトボックス暗号に関する概要と 2012 年時点の現状をサーベイした論文。

  1. Brecht Wyseur. white-box cryptography: hiding keys in software, MISC magazine, April 2012.