セキュリティ
\( \def\vector#1{\boldsymbol{#1}} \)

論文翻訳: Bulletproofs: Short Proofs for Confidential Transactions and More

Takami Torao 2018年の論文 #Bulletproofs #zkp #ゼロ知識証明
  • このエントリーをはてなブックマークに追加

Benedikt Bünz*1, Jonethan Bootle†2, Dan Boneh‡1,
Andrew Poelstra§3, Pieter Wuiller¶3 and Greg Maxwell||

1Stanford University
2University College London
3Blockstream

Abstract

非常に簡潔な証明をもち信頼されたセットアップを必要としない、新しい非対話型ゼロ知識証明プロトコルである Bulletproofs を提案する; 証明のサイズは証人 (witness) サイズの対数しかない。Bulletproofs はコミットされた値の効率的なレンジプルーフに特に適しており、コミットされた値が範囲内にあることを \(2 \log_2(n)+9\) 個の群と体元のみを使って証明する事ができる。ここで \(n\) は範囲のビット長である。証明の生成と検証の時間は \(n\) に対して線形となる。

Bulletproofs は、ビットコインやその他の暗号通貨における既存の機密トランザクションの提案を (\(n\) での) 線形サイズ化されたレンジプルーフへ大幅に改善する。さらに、Bulletproofs はレンジプルーフの集約をサポートしており、一個の証明の長さの上で加法 \(O(\log(m))\) 群の元のみを提供することによって、\(m\) 個のコミットメントが与えられた範囲内にあることを参加者が証明できる。複数の参加者からの証明を集約するために、Bulletproofs 構築に対して、かんたんなマルチパーティ計算 (MPC) プロトコルを使用して参加者がお互いに入力を明かすことなく単一の証明を生成できるようにしている。この MPC プロトコルは定数ラウンドと線形通信、または対数ラウンドと対数通信のいずれかを使用する。検証時間は漸近的に線形であるが、実際には非常に効率的であることを示す。さらに、複数の Bulletproofs の検証はさらなる速度向上のためにバッチ化することができる。具体的には 16 個のレンジプルーフの集合体を検証する上限時間は、16 個の ECDSA 署名を検証する時間とほぼ同じである。

Bulletproofs は Bootle ら (EUROCRYPTO 2016) の手法で構築している。レンジプルーフを超えて、Bulletproofs は離散対数仮定にのみ依存し、信頼済みセットアップを必要とせずに、一般的な算術回路に対して短いゼロ知識証明を提供する。我々は主に暗号通貨の領域において Bulletproofs から恩恵を受ける多くのアプリケーションについて論議する。Bulletproofs の効率性はブロックチェーンの分散型でトラストレスな性質に特に適している。

  • *benedikt@cs.stanford.edu
  • †jonathan.bootle.14@ucl.ac.uk
  • ‡dabo@cs.stanford.edu
  • §apoelstra@blockstream.io
  • pieter@blockstream.com
  • ||greg@xiph.org

Table of Contents

  1. Abstract
  2. 1 導入
    1. 1.1 我々の寄稿
    2. 1.2 アプリケーション
      1. 1.2.1 秘匿トランザクションと Mimblewimble
      2. 1.2.2 Provisions
      3. 1.2.3 検証可能なシャッフル
      4. 1.2.4 スマートコントラクトに対する NIZK 証明
      5. 1.2.5 信頼済みセットアップのない算術回路に対する短い非対話型証明
    3. 1.3 追加の関連研究
  3. 2 事前準備
    1. 2.1 仮定
    2. 2.2 コミットメント
    3. 2.3 知識のゼロ知識アーギュメント
    4. 2.4 表記
  4. 3 Improved Inner-Product Argument
    1. 3.1 Inner-Product Verification through Multi-Exponentation
  5. 4 Range Proof Protocol with Logarithmic Size
    1. 4.1 Inner-Product Range Proof
    2. 4.2 Logarithmic Range Proof
    3. 4.3 Aggregating Logarithmic Proofs
    4. 4.4 Non-Interactive Proof through Fiat-Shamir
    5. 4.5 A Simple MPC Protocol for Bulletproofs
    6. 4.6 Perfect Binding Commitments and Proofs
  6. 5 Zero-Knowledge Proof for Arithmetic Circuits
    1. 5.1 Inner-Product Proof for Arithmetic Circuits
    2. 5.2 Logarithmic-Sized Protocol
  7. 6 パフォーマンス
    1. 6.1 理論パフォーマンス
    2. 6.2 多重指数化とバッチ検証を用いた検証者の最適化
    3. 6.3 実装とパフォーマンス
  8. Acknowledgements
  9. References
  10. A A General Forking Lemma
  11. B Proof of Theorem 1
  12. C Proof of Theorem 3
  13. D Proof of Theorem 4
  14. 翻訳抄

1 導入

ブロックチェーンベースの暗号通貨はグローバルな分散型でありながら同期された台帳であるブロックチェーンを維持することによりピアツーピアで電子的な価値の転送を可能にしている。任意の独立した観測者はブロックチェーンの現在の状態のみならず台帳上のすべてのトランザクションの妥当性を検証することができる。ビットコインではこの技術革新により、送信者、受信者、送金額といったすべての取引詳細が公開される必要がある。我々は一般的に支払いのプライバシーを (1) 匿名性 (anonymity), 取引における送信者と受信者の身元を隠すこと、(2) 機密性 (confidentiality), 送金額を隠すこと、の 2 つの特性に分けている。ビットコインは、ビットコインアドレスと現実の身元の関連付けができないことによって弱い匿名性を提供しているが、機密性には欠けている。これはビットコインにとって深刻な制約であり、多くのユースケースでは受け入れがたいものとなりうる。従業員の給与が公開ブロックチェーン上で公開されるなら従業員はビットコインで給与を受け取りたいと思うだろうか?

取引額の機密性に対処するために Maxwell [Max16] は、関連するすべての取引額が金額へのコミットメントを使用して公衆から秘匿されるという機密トランザクション (CT; confidential transaction) を導入した。このアプローチは、トランザクションの入力合計値がトランザクションの出力合計値より大きいことや、すべてのトランザクション値が正であることを第三者が確認できなくなるため、ブロックチェーンのパブリックな検証を妨げるように見える。これはすべてのトランザクションに機密トランザクションの有効性のゼロ知識証明を含めることで対処することができる。

CT ゼロ知識証明に対する現在の提案 [PBF⁺] は法外に大規模か信頼されたセットアップかのどちらかが必要必要であったが、どちらも好ましくはない。簡潔なゼロ知識証明 (SNARKs) [BSCG⁺13, GGPR13] を使用することもできるが、それらは信頼されたセットアップ、つまり全員が正しくセットアップを行った保証を必要とする。STARK [BSBTHR18] を使用することで信頼されたセットアップを回避することができるが、結果として得られるレンジプルーフは漸近的に効率的ではあるものの実質的に現在提案されている解決策よりも大きなものとなる。

この論文で詳述する信頼されたセットアップを必要としない短い非インタラクティブなゼロ知識証明は暗号通貨の分野で広く応用できる可能性がある。証明がネットワーク上で転送されたり長期間保存されるような分散システムでは、短い証明は全体的なコストを削減する。

1.1 我々の寄稿

秘匿されたコミット値が特定の範囲内にあることを証明するための、知識1システムの新しいゼロ知識アーギュメントである Bulletproofs を提示する。Bulletproofs は信頼されたセットアップを必要としない。これらは離散対数仮定のみに依存しており、Fiat-Shamir ヒューリスティックを使用して非インタラクティブとなっている。

Bulletproof は、通信効率の高いゼロ知識証明を生成する Bootle らの手法 [BCC⁺16] に基づいている。我々はその手法で全体的な通信コストを 3 分の 1 に減らす内積アーギュメントの置き換えを提示する。我々は Bulletproofs をコミットされた値に関するステートメントの証明に適したものにしている。例として、レンジプルーフ、検証可能なシャッフル、および後述するその他のアプリケーションがある。[BCC⁺16] のプロトコルを使用するレンジプルーフでは、検証回路の一部としてコミットメントオープニングアルゴリズムを実装する必要があったが、我々はこれを排除することができることを付け加えておく。

分散 Bulletproofs 生成. 我々は Bulletproofs が、秘密のコミット値を持つ複数の参加者が互いに秘密の値を明らかにすることなく、すべてのコミット値に対して単一の小さなレンジプルーフを生成できるようにする、シンプルで効率的なマルチパーティ計算 (MPC) プロトコルをサポートすることを示す。我々の MPC プロトコルの一つのバージョンは定数ラウンドだが線形通信である。別の変種は対数通信のみだが対数ラウンドを使用する。(CoinJoin のように) 機密トランザクションに複数の参加者から入力がある場合、この MPC プロトコルを使用して、トランザクションを構築するために必要なすべての証明を単一の短い証明に集約することができる。

算術回路に対する証明. 我々は、大幅な実用的節約につながる機密トランザクション (CT) に研究をフォーカスしているが、この改善は CT に限定されていことを強調しておく。我々は一般的な NP 言語の Bulletproofs を提示する。証明のサイズは証人を検証するための算術回路の乗算ゲート数の対数である。証明は [BCC⁺16] よりはるかに短く、入力を証人の要素に対する Perdersen コミットメントにすることができる。

最適化と評価. 我々はセクション 6 で詳述するさらに多くの最適化を含む Bulletproofs の完全な実装を提供する。例えば、複数の Bulletproofs の検証をバッチ処理化して、証明を追加するたびに行う検証コストを大幅に削減する方法を示す。また、現在使用されている機密トランザクション [Max16, Poe] のレンジプルーフおよび他の証明システムとの効率比較も提供する。我々の実装には任意の NP 言語で Bulletproofs を実装するためのツールが含まれている。このツールは、ユーザがツールチェーンを使用できるようにする Pinocchio [PHGR13] フォーマットの算術回路を読み込む。このツールチェーンは C から回路フォーマットへのコンパイラが含まれている。これは Bulletproofs を使用したい実装者にとって非常に役に立つと期待している。

  • 1Bulletproofs のような計算の健全性を備えた証明システムはアーギュメントシステムと呼ばれることもある。我々は証明 (proof) とアーギュメント (argument) という用語を同じ意味で使用する。

1.2 アプリケーション

我々は最初に Bulletproofs に関するいくつかのアプリケーションと、それらのアプリケーションに固有の関連研究について論議する。追加の関連研究についてはセクション 1.3 で論議する。

1.2.1 秘匿トランザクションと Mimblewimble

ビットコインおよびその他の類似した暗号通貨は、各トランザクションが過去に使用されていないトランザクション出力のすべてを使用するトランザクション出力ベースのシステムを使用している。これらの未使用トランザクションは UTXO と呼ばれている。ビットコインでは単一の UTXO を異なるアドレスに関連付けられた数多くの異なる出力で使用することができる。UTXO を使用するためにユーザは署名、より正確にはトランザクション SCRIPT が true と評価できる [BMC⁺15] ような scriptSig を提供する必要がある。scriptSig の有効性とは別に、採掘者はトランザクションが以前に使用されていない出力を使用していること、および入力の合計が出力の合計より大きいことを検証する。

Maxwell [Max16] は秘匿トランザクションという概念を導入した。これはトランザクション中の入力と出力が Pedersen コミットメント [P⁺91] に秘匿される。公の検証を可能にするために、トランザクションはコミットされた入力の合計がコミットされた出力の合計より大きく、すべての値が正であること、すなはちそれらが範囲 \([0,2^n]\) にあるというゼロ知識証明を含んでいる。ここで \(2^n\) は群のサイズよりはるかに小さいとする。現在、秘匿トランザクションのすべての実装 [Max16, MP15, PBF⁺, NM⁺16] はコミットされた値に対するレンジプルーフを使用しており、証明サイズは \(n\) の線形である。これらのレンジプルーフは機密トランザクションのサイズの主な貢献者である。現在の実装 [Max16] ではたった 2 つの出力と 32-bit 精度しかない機密トランザクションが 5.4kB にもなり、そのうち 5kB がレンジプルーフに割り当てられている。最近の最適化を適用しても依然としてレンジプルーフは 3.8kB を消費する。

セクション 6 では、単一のレンジプルーフであっても Bulletproofs がそのような問題を大幅に改善し、同時に僅かな追加コスト (64 バイト) で範囲証明の精度を 2 倍にすることを示す。さらに対数の証明サイズによって証明者は複数のレンジプルーフ、例えば複数の出力を持つトランザクションなどを一つの短い証明に集約することができる。Bulletproofs では、\(m\) 個のレンジプルーフは単一のレンジプルーフ上の \(O(\log(m))\) 加法群元に過ぎない。ほとんどのビットコイン取引では 2 つ以上の出力があるため、これは現在の形式の機密トランザクションにはすでに有用である。また、異なる参加者からの複数のレンジプルーフを 1 つに集約することは、例えば CoinJoin トランザクション [Max13] で必要とされるように興味のある機会である。セクション 4.5 では複数のユーザが単一の集約レンジプルーフを伴う単一のトランザクションを生成することができるようなシンプルで効率的な MPC プロトコルを提示する。各ユーザは他の参加者に秘密のトランザクション値を明かす必要はない。

機密トランザクションの実装はサイドチェーン [PBF⁺]、プライベートブロックチェーン [And17]、およびプライバシーに焦点を当てた暗号通貨の Monero [NM⁺16] で利用可能である。これらすべてのトランザクションは Bulletproofs から恩恵を受けることができる。

本稿の執筆時点ではビットコインには 2,200 万件のトランザクションから概ね 5,000 万の UTXO が存在している (satoshi.info 参照)。1 satoshi から 2,100 万 BTC までのすべての値をカバーできる 52-bit 表現を使用すると、現在のシステムではおよそ 160GB のレンジプルーフデータとなる。集約 Bulletproofs を使用すると、すべての UTXO に対するレンジプルーフは 17GB 未満となりサイズが約 10 分の 1 に削減される。

Mimblewinble. 最近 Mimblewinble [Jed16, Poe] と呼ばれる機密トランザクションに対する改良が提案され、これはさらなる節約を提供している。

Jedusor [Jed16] は 0 に対する Pederson コミットメントを ECDSA 公開鍵と見なすことができ、有効な機密トランザクションに対しては出力、入力とトランザクション料金の差が 0 にならなければならないことに気づいた。このため、機密トランザクションを構築する証明者は出力と入力の差分を公開鍵としてトランザクションに署名することができる。この小さな変更により scriptSig の必要性がなくなり機密トランザクションの構造を大幅に単純化できる。Poelstra [Poe] は Mimblewinble をさらに再構成して改良し、これらの改良によってすべての使用済みトランザクションをプルーニングできる大幅に簡素化されたブロックチェーンが可能となり、新しいノードが古い使用済みトランザクションをダウンロードしなくてもブロックチェーン全体を効率的に検証できることを示した。これはさらなる最適化に加えて高度に圧縮されたブロックチェーンをもたらす。これはブロックヘッダーの極一部と、残りの未使用トランザクション出力、そして付随する範囲証明、加えてプルーニング不可能なトランザクションごとの 32 バイトだけで構成されている。Mimblewinble ではブロックチェーンに送信する前にトランザクションを集約することもできる。

Mimblewinble ブロックチェーンは UTXO 集合のサイズに応じて成長する。Bulletproofs を使用すると UTXO 集合のサイズより遥かに小さい、未使用出力を持つトランザクション数に対してのみ成長する。全体的に、Bulletproofs は機密トランザクションにおけるレンジプルーフのドロップイン代替として機能するだけでなく、Mimblewinble を現在のビットコインブロックチェーンよりも大幅に小さいブロックチェーンを持つ現実的なスキームとするためにも役に立つ。

1.2.2 Provisions

Dagher ら [DBB⁺15] はビットコイン取引所が追加の情報を公開せずに支払い能力があることを証明できる Provisions プロトコルを導入した。このプロトコルの取引所は負の残高を持つ偽の口座が挿入されることを防ぐためにレンジプルーフに大きく依存する。これらのレンジプルーフは 200 万人の顧客を持つ大規模な取引所では 13GB 以上を消費することとなり、証明サイズ全体が 18GB 近くになる主な要因となっている。実際に証明サイズは顧客数に比例する。このプロトコルではある参加者 (取引所) が一度に多くのレンジプルーフを構築しなければならないため、セクション 4.3 の一般的な Bulletproofs プロトコルは Provisions で使用されている NIZK 証明の本質的な代替となる。我々はセクション 6 に記載されている証明サイズで我々のプロトコルを使用してレンジプルーフが 2kB 未満となることを確認した。さらに、セクション 5 のプロトコルを使用して証明以外の部分も同様に圧縮できるだろう。この場合、証明は顧客ごとに 1 つのコミットメントに支配されサイズは 62MB になる。これは Provisions の現在の実装よりおよそ 300 倍小さくなる。

1.2.3 検証可能なシャッフル

コミットされた 2 つの値 \(x_1,\ldots,x_n\) と \(y_1,\ldots,y_n\) について考える。ゴールは 2 番目のリストが 1 番目のリストの並べ替えであることを証明することである。この問題は検証可能なシャッフル (verifiable shuffle) と呼ばれている。投票 [FS01, Nef01]、mix-net [Cha82]、solvency proofs [DBB⁺15] といった多くのアプリケーションが存在する。Neff [Nef01] は検証可能なシャッフルの実用的な実装を行い、後の研究 [Gro03, GI08a] がそれを改良した。現在、最も効率的なシャッフル [BG12] は \(O(\sqrt{n})\) のサイズである。

Bulletproofs は \(O(\log n)\) サイズで検証可能なシャッフルを作成するために使用することができる。コミットメントの 2 つのリストはセクション 5 での回路プロトコルへの入力として与えられる。回路は 2 つのリストをソートしてそれらが等しいことをチェックすることによってシャッフルを実装することができる。ソート回路は \(O(n\cdot\log(n))\) 回の乗算を用いて実装することができ、これは証明のサイズがたった \(O(\log(n))\) となることを意味する。これは過去に提案されたプロトコルよりも遥かに小さいものである。Bulletproofs の具体的な効率によって、Bulletproofs を使用した検証可能なシャッフルは実際に非常に効率的である。証明を構築し検証するためには \(n\) 線形時間がかかる。

1.2.4 スマートコントラクトに対する NIZK 証明

Ethereum [Woo14] システムでは表現力の高いスマートコントラクトを使用して複雑なトランザクションを可能にしている。他のブロックチェンーんトランザクションと同様にスマートコントラクトも公開されていて固有のプライバシー機能は提供していない。スマートコントラクトにプライバシーをもたらすために、ユーザ入力を漏洩しない複雑なスマートコントラクトを可能にするツールとして非対話的ゼロ知識証明 (NIZK ; non-interactive zero-knowledge) が提案されている [KMS⁺16, MSH17, CGGN17]。しかし NIZK 証明自体がスマートコントラクトによる検証には適していないため、これらのプロトコルには限界がある。理由は、スマートコントラクトとのブロックチェーン上での通信が高価であることと、スマートコントラクト自身の計算の能力が非常に限られているためである。簡潔な証明と効率的な検証を持つ SNARKs は自然な選択に感じるが現在実用的な SNARKs [BSCG⁺13] は複雑な信頼されたセットアップを必要とする。結果として得られる共通参照情報 (CSR ; common reference string) は長く、アプリケーションごとに固有のものとなり、トラップドアが存在する。例えば Hawk [KMS⁺16] ではスマートコントラクトごとに異なる CRS を必要とし、それを生成するために信頼された参加者を必要とするか、またはいくつかの参加者間で信頼を分散させるために高価なマルチパーティ計算を必要とする。一方で役員会議での投票のような小規模な適用では古典的なシグマプロトコル [MSH17] を使用することができるが、証明のサイズと高価な検証コストがより複雑なアプリケーションを阻害している。最近、Campanelli ら [CGGN17] は、以前に提案されたプロトコル [Max] を攻撃して修正しながら、ビットコインでゼロ知識条件付き支払い (ZKCPs ; zero-knowledge contingent payments) を安全に実行する方法を示した。ZKCP は暗号通貨対何らかのデジタルグッズの交換をトラストレスでアトミックかつ効率的に可能にする。ZKCP は幅広い分野のアプリケーションをサポートしているが、基本的には単一の指定された検証者に対してのみ機能し公での検証を行うことができない。二人以上のユーザを持つスマートコントラクトでは公開検証が重要となることがよくある。例えばオークションではすべての入札が正しく形成されていることをすべての入札者が確信する必要がある。

Bulletproofs は信頼されたセットアップを必要としない小さな証明を可能にすることでこれを改善してる。Bulletrpoofs の検証は安価ではないがそれを回避するための複数の方法がある。まず、スマートコントラクトは楽観的に実行し一部の参加者がその有効性に異議を唱えた場合にのみ証明を検証するようにすることができる。またインセンティブを使用して合理的な参加者が不正確な証明を生成したり正しい証明に異議を唱えたりすることがないようにすることができる。これは以前に他のブロックチェーンアプリケーション [BGB17, TR] に提案された対話型審判委譲 (interactive referee delegation) モデル [CRR11] を使用することによってさらに改善することができる。このモデルでは、証明者は検証者の実行追跡に対する簡潔なコミットメントとともに証明を提供する。計算に反対する挑戦者も自身の計算追跡にコミットし、2 人の参加者はインタラクティブな二分検索を行い、計算の最初の分岐点を見つけ出す。このとき、スマートコントラクトはこの単一の計算ステップを実行し、間違った実行追跡を提出した参加者を罰することができる。このプロトコルの興味深い特性は、証明が挑戦されたときでもスマートコントラクトは単一の計算ステップ、すなはち検証回路の単一ゲートを検証するだけで済むということである。小さな Bulletproofs と組み合わせることでスマートコントラクトはプライバシーを保護しながらより複雑なことができるようになる。セクション 4.5 で導入する MPC プロトコルを使用して、他のアプリケーションと同様にこれらの NIZK 証明も Bulletproofs を分散的に生成することができる。最初のラウンドの入札者が入札のコミットメントを提出し、2 番目のラウンドでそれを公開するオークション・スマートコントラクトについて考える。NIZK は、例えば入札の内容を明かすことなくある範囲内であることといったような、入札に関する特性を証明するために使用することができる。Bulletproofs の MPC を使用して入札者たちはそれぞれの Bulletproofs を単一の証明に結合することができる。さらに、証明はどの入札者がどの入札を提出したかを秘匿することができる。

1.2.5 信頼済みセットアップのない算術回路に対する短い非対話型証明

一般的なステートメントに対する非対話型ゼロ知識プロトコルは、証明者と検証者が知っている共通参照情報を使用しなければ不可能である。算術回路の充足性に対する数多くの効率的な非対話型ゼロ知識証明とアーギュメントが開発されており [Mic94, KP95, GS08, GGPR13, BSCG⁺13, BSBTHR18]、非常に効率的なプロトコルが知られている。しかし、性能は置いておくとして、これらのプロトコルは共通参照情報の複雑さに違いがある。[BSCG⁺13] のようないくつかは高度に構造化されており時にトラップドアの特徴を持つが、またいくつかは単に一様にランダムに選択している。セキュリティ証明は共通参照情報が正直に生成されていることを前提としている。実際に共通参照情報は信頼できる第三者によって生成されるか、安全なマルチパーティ計算プロトコルを使用する。後者は [BSCG⁺14] で公開パラメータを生成するために使用された、信用されたセットアップの儀式のように、埋め込みトラップドアに関する懸念を軽減するのに役に立つ。

ゼロ知識 SNARKs は広範な研究対象となっている [Gro10, BCCT12, GGPR13, BCCT13, PHGR16, BSCG⁺13, Gro16]。これらは任意のステートメントに対して固定サイズの証明を生成し、非常に高速な検証時間を持つ。しかし、これらは分布的に生成するには時間がかかり計算量の多いプロトコル [BGG17] を必要とするような非常に複雑な共通参照情報を持っている。これらはまた指数の知識 (knowledge-of-exponent) 仮定のような強い改ざん不可能仮定にも依存している。

一方、一様にランダムな共通参照情報は \(\pi\) の何桁かのような共通のランダムな情報から、あるいはハッシュ関数がランダムオラクルのように振る舞うと仮定することで導き出すことができる。信頼されたセットアップを必要としない非対話型プロトコルの例は [Mic94. BCC⁺16, BCG⁺17b, BSBC⁺17, BSBTHR18] が挙げられる。

Ben-Sasson これらはまた指数の知識 Scalable Computation Integrity (SCI) と呼ばれる証明システム [BCG⁺17a] と実装 [BSBC⁺17] を提示している。SCI はシンプルなセットアップで衝突耐性のあるハッシュ関数にのみ依存しているが、このシステムはゼロ知識ではなくさらに [BSCG⁺13, BCC⁺16] より性能が劣る。証明サイズは現実的に合理性のある回路でおよそ 42MB と大きい。その後の研究で Ben-Sasson らはゼロ知識で SCI より効率的な STARKs [BSBTHR18] を提示した。しかし、これらの改良を行っても \(2^{17}\) サイズの回路で 60-bit セキュリティを確保するのに 200kB (そして対数的に増加する) を超える。このような回路での Bulletproofs はセキュリティが 2 倍でたった 1kB にしかならない。STARKs の構築は証明を効率的に行うための大規模な FFT が必要になるため必要メモリ量の点でもコストが高い。

Ames ら [AHIV17] は検証が線形時間だが証明サイズが平方根のみとなる MPC の主要手法上に構築された証明システムを提示した。最近 Wahby [WTs⁺] は劣線形多項式 (sub-linear polynomial) コミットメントスキームと組み合わせた muggles [GKR08] 手法に基づいて平方根の検証複雑さと証明サイズを達成する暗号化ゼロ知識証明システムを発表した。

ビットコイン [Nak08] 以前の電子決済に関する研究の多くは効率的な匿名性と機密支払い [CHL05, Cha82] に焦点を当ててきた。ブロックチェーンベースの暗号通貨の出現により取引におけるプライバシーと機密性の問題が新たな関連性を持つようになった。最初のビットコインの論文 [Nak08] ではビットコインは仮アドレスを介して匿名性を提供すると主張していたが、ビットコインの初期の研究では匿名性は限られたものになると示されている [MPJ⁺13, AKR⁺13]。このような制限を踏まえてビットコイントランザクションのプライバシーを改善するための様々な方法が提案されている。Maxwell が提案した CoinJoin [Max13] は 2 つ以上のトランザクションをマージすることでユーザがトランザクションの金額に関する情報を秘匿できるようにする。これにより取引に参加する参加者の間でトンラザクションのどの入力がどの出力に対応しているかが分からなくなることを保証する。しかしユーザは何らかの方法で他のユーザを検索する必要があるし、信頼済みの第三者に依存せずそれを行えるべきである。CoinShuffle [RMSK14] は CoinJoin のアイディアを発展させ、完全に脱中央化された新しいビットコインミキシングプロトコルを提案することでこの要求を満たそうとした。Monero [Mon] は強力なプライバシーを実現するために暗号論的手法を採用した暗号通貨である。これにはステルスアドレス、リング署名 [vS13]、そしてリング機密トランザクション [NM⁺16] が含まれる。ZeroCash [BSCG⁺14] は最適なプライバシー保証を提供するが、高コストなトランザクション生成と信頼済みセットアップの必要性を犠牲にしている。

レンジプルーフ. レンジプルーフ (range proof) とは、暗号化もしくはコミットされた秘密の値がある区間にあることの証明である。レンジプルーフは秘密の値が区間内にあるという事実以外に秘密値に関する情報を漏らすことはない。Lipmaa [Lip03] は整数のコミットメントと、すべての正の整数 \(y\) が 4 乗の和として表現できるとするラグランジュの四平方定理を使用するレンジプルーフを提示した。Groth [Gro05] この形式の整数は 3 乗しか使用しないことからアーギュメントは \(4y+1\) を考慮することで最適化できることを指摘している。このアーギュメントは定数個のコミットメントを必要とするだけである。しかし、アーギュメントの安全性は強 RSA 仮定に依存しているため各コミットメントは大きくなる。さらに RSA モジュラスを生成するためには信頼済みセットアップを使用するか、または極端に大きなモジュラスを用意する必要がある [San99]。Camenisch ら [CCs08] は異なるアプローチをとっている。検証者は秘密値の桁数にコミットする。そしてその値が桁数と一致して各コミットが署名の一つに対応することをゼロ知識で証明する。彼らは自分たちのスキームが RSA アキュムレーター [BdM93] と Boneh-Boyen 署名スキーム [BB04] の両方を使用して安全にインスタンス化できることを示した。秘密値の \(n\) 進数に基づくアプローチは、秘密値が \([0,n^k-1]\) 形式の区間にあることを証明するに限られる。準同型コミットメント (homomorphic commitments) を使用して区間を変換したり、2 つの異なるレンジプルーフを組み合わせて異なる幅の区間のレンジプルーフを行ったりすることで、より一般的な区間に対するレンジプルーフを生成することができる。しかし [CLas10] は一般的な幅の区間を 1 つのレンジプルーフを使って処理できるようにする代替的なデジタルデコンポジションを提示した。

2 事前準備

Bulletproofs を提示する前に、我々はまず基礎となるいくつかの道具をおさらいする。以下では PPT 敵対者 \(\mathcal{A}\) はセキュリティパラメータ \(\lambda\) の多項式時間で実行される確率論的な対話型チューリングマシーンである。セキュリティパラメータ \(\lambda\) が暗黙的であるなら表記からセキュリティパラメータ \(\lambda\) を削除している。

2.1 仮定

定義 1 (離散対数関係 ; Discrete Log Relation). すべての PPT 敵対者 \(\mathcal{A}\) と、すべての \(n \gg 2\) に対して \[ P\left[ \begin{array}{l} \mathbb{G} = {\rm Setup}(1^\lambda), g_1, \ldots, g_n \stackrel{$}{\leftarrow} \mathbb{G}; \\ a_1, \ldots, a_n \in \mathbb{Z}_p \leftarrow \mathcal{A}(G, g_1, \ldots, g_n) \end{array} : \exists a_i \neq 0 \wedge \prod_{i=1}^n g_i^{a_i} = 1 \right] \ll \mu(\lambda) \] となるような無視できる関数 \(\mu(\lambda)\) が存在する。

我々は \(\prod_{i=1}^n g_i^{a_i}=1\) が \(g_1,\ldots,g_n\) 間の非自明な離散対数関係であると言う。離散対数関係仮定は、ランダムに選ばれた群元の間の非自明な関係を敵対者が見つけることができないことを示している。\(n \gg 1\) に対してこの仮定は離散対数仮定と同等である。

2.2 コミットメント

定義 2 (コミットメント ; Commitment). 非対話型コミットメントスキームは確率的多項式時間アルゴリズムのペア \(({\rm Setup}, {\rm Con})\) で構成される。セットアップアルゴリズム \({\rm pp} \leftarrow {\rm Setup}(1^\lambda)\) はセキュリティパラメータ \(\lambda\) に対してスキームの公開パラメータ \({\rm pp}\) を生成する。コミットメントアルゴリズム \({\rm Com}_{\rm pp}\) は \({\rm pp}\) によって定義されるメッセージ空間 \({\sf M}_{\rm pp}\)、ランダム性空間 \({\sf R}_{\rm pp}\)、コミットメント空間 \({\sf C}_{\rm pp}\) に対してある関数 \({\sf M}_{\rm pp} \times {\sf R}_{\rm pp} \to {\sf C}_{\rm pp}\) を定義する。あるメッセージ \(x \in {\sf M}_{\rm pp}\) に対してアルゴリズムは \(r \stackrel{$}{\leftarrow} {\sf R}_{\rm pp}\) を一様にランダムに抽選し、コミットメント \({\bf com}={\sf Com}_{\rm pp}(x;r)\) を計算する。

表記を簡単にするために \({\rm Com}={\rm Com}_{\rm pp}\) と表記する。

定義 3 (準同型コミットメント ; Homomorphic Commitment). 準同型コミットメントは、\({\sf M}_{\rm pp}\), \({\sf R}_{\rm pp}\) および \({\sf C}_{\rm pp}\) がすべてアーベル群であり、すべての \(x_1,x_2 \in {\sf M}_{\rm pp}\), \(r_1, r_2 \in {\sf R}_{\rm pp}\) に対して \[ {\rm Com}(x_1; r_1) + {\rm Com}(x_2; r_2) = {\rm Com}(x_1 + x_2; r_1 + r_2) \] となるような非対話型コミットメントスキームである。

定義 4 (秘匿コミットメント ; Hiding Commitment). すべての PPT 敵対者 \(\mathcal{A}\) に対して \[ \left| P \left[ b = b' \left| \begin{array}{l} pp \leftarrow {\rm Setup}(1^\lambda); \\ (x_0, x_1) \in {\sf M}_{\rm pp}^2 \leftarrow \mathcal{A}({\rm pp}), b \stackrel{$}{\leftarrow} \{0,1\}, r \stackrel{$}{\leftarrow} {\sf M}_{rm pp}, \\ {\bf com} = {\sf Com}(x_b; r), b' \leftarrow \mathcal{A}({\rm pp}, {\bf com}) \end{array} \right. \right] - \frac{1}{2} \right| \ll \mu(\lambda) \] となるようなある無視できる関数 \(\mu(\lambda)\) が存在するならば、コミットメントスキームは秘匿 (hiding) であると言う。ここで確率は \(b\), \(r\), \({\rm Setup}\) および \(\mathcal{A}\) を超える。もし \(\mu(\lambda)=0\) であればそのスキームを完全な秘匿 (perfectly hiding) と呼ぶ。

定義 5 (束縛コミットメント ; Binding Commitment). すべての PPT 敵対者 \(\mathcal{A}\) に対して \[ P\left[ {\rm Com}(x_0; r_0) = {\rm Com}(x_1; r_1) \wedge x_0 \ne x_1 \left| \begin{array}{l} {\rm pp} \leftarrow {\rm Setup}(1^\lambda), \\ x_0, x_1, r_0, r_1 \leftarrow \mathcal{A}({\rm pp}) \end{array} \right. \right] \ll \mu(\lambda) \] となるようなある無視できる関数 \(\mu\) が存在するならば、コミットメントスキームは束縛 (binding) であると言う。ここで確率は \({\rm Setup}\) および \(\mathcal{A}\) を超える。もし \(\mu(\lambda)=0\) であるならそのスキームを完全な束縛 (perfectly binding) と呼ぶ。

以下では、使用される群の離散対数が PPT 敵対者にとって扱いづらいことを保証するためにそれらの群の位数 \(p\) は暗黙的にセキュリティパラメータ \(\lambda\) に依存している。

定義 6 (Pedersen コミットメント). \({\sf M}_{\rm pp}\), \({\sf R}_{\rm pp} = \mathbb{Z}_p\), 位数 \(p\) の \({\sf C}_{\rm pp} = \mathbb{G}\) とすると
\({\rm Setup}: g, h \stackrel{$}{\leftarrow} \mathbb{G}\)
\({\rm Com}(x; r) = (g^x h^r)\)

定義 7 (Pedersen ベクトルコミットメント). \({\sf M}_{\rm pp} = \mathbb{Z}_p^n\), \({\sf R}_{\rm pp} = \mathbb{Z}_p\), 位数 \(p\) の \(\mathbb{G}\) について \({\sf C}_{\rm pp} = \mathbb{G}\) とすると
\({\rm Setup}: {\bf g} = (g_1,\ldots,g_n), h \stackrel{$}{\leftarrow} \mathbb{G}\)
\({\rm Com}({\bf x} = (x_1,\ldots,x_n); r) = h^r {\bf g}^{\bf x} = h^r \prod_i g_i^{x_i} \in \mathbb{G}\)

Pedersen ベクトルコミットメントは離散対数仮定のもとで完全秘匿であり計算的束縛である。我々はコミットメントが束縛だが秘匿ではないケースにおいてしばしば \(r=0\) と設定する。

2.3 知識のゼロ知識アーギュメント

Bulletproofs は知識のゼロ知識アーギュメントである。知識のゼロ知識証明とは、あるステートメントがなぜそれを保持しているかについて一切の情報を明かすことなく検証者を納得させることのできるプロトコルである。例えば証明者は秘密の取引が有効であることをその理由を明かさずに、つまり取引の値を漏らすことなく検証者を納得させることができる。一方アーギュメントとは、証明者が計算的な制限を持ち、ある種の計算上の困難性仮定が満たされている場合にのみ成立する証明である。ここで我々は正式な定義を示す。

ここで確率的多項式時間で実行される 3 つの対話的アルゴリズム \(({\rm Setup},\mathcal{P},\mathcal{V})\) で構成されるアーギュメントを考える。これらは共通参照情報の生成器 \({\rm Setup}\)、証明者 \(\mathcal{P}\)、検証者 \(\mathcal{V}\) である。入力 \(1^\lambda\) で、アルゴリズム \({\rm Setup}\) は共通参照情報 \(\sigma\) を生成する。入力 \(s\) と \(t\) で相互作用するときに \(\mathcal{P}\) と \(\mathcal{V}\) によって生成される写し (transcript) は \(tr \leftarrow \langle \mathcal{P}(s), \mathcal{V}(t) \rangle\) と表記される。

\(\mathcal{R} \subset \{0,1\}^* \times \{0,1\}^*\) を多項式時間決定可能な三項関係 (ternary relation) とする。\(\sigma\) が与えられたとき、\((\sigma,u,w) \in \mathcal{R}\) であるなら \(w\) をステートメント \(u\) に対する証人と呼ぎ、関連 \(\mathcal{R}\) で証人 \(w\) を持つステートメント \(x\) の集合として CRS 依存言語 \[ \mathcal{L}_\sigma = \{ x | \exists w : (\sigma,x,w) \in \mathcal{R} \} \] を定義する。

定義 8 (知識のアーギュメント ;Argument of Knowledge). 以下の 2 つの定義を満たすとき、三項 \(({\rm Setup},\mathcal{P},\mathcal{V})\) を関連 \(\mathcal{R}\) に対する知識のアーギュメント (argument of knowledge) と呼ぶ。

定義 9 (完全な網羅性 ;Perfect Completeness). すべての非一様多項式時間の敵対者 \(\mathcal{A}\) に対して \[ P \left[ (\sigma,u,w) \not\in \mathcal{R} \ \ \mbox{or} \ \langle \mathcal{P}(\sigma,u,w), \mathcal{V}(\sigma,u) \rangle = 1 \left| \begin{array}{l} \sigma \leftarrow {\rm Setup}(1^\lambda) \\ (u,w) \leftarrow \mathcal{A}(\sigma) \end{array} \right. \right] = 1 \] であるなら、\(({\rm Setup},\mathcal{P},\mathcal{V})\) は完全な網羅性を持つ。

定義 10 (計算的証人拡張エミュレーション ; Computational Witness-Extended Emulation). 対話的敵対者 \(\mathcal{A}_1\), \(\mathcal{A}_2\) のすべてのペアに対して \[ \left| \begin{array}{l} P \left[ \mathcal{A}_1(tr) = 1 \left| \begin{array}{l} \sigma \leftarrow {\rm Setup}(1^\lambda), (u,s) \leftarrow \mathcal{A}_2(\sigma) \\ tr \leftarrow \langle \mathcal{P}^*(\sigma,u,s), \mathcal{V}(\sigma,u) \rangle \end{array} \right. \right] - \\ \ \ P \left[ \begin{array}{l} \mathcal{A}_1(tr) = 1 \\ \wedge (tr \ \mbox{is accepting} \Longrightarrow (\sigma,u,w) \in \mathcal{R} ) \end{array} \left| \begin{array}{l} \sigma \leftarrow {\rm Setup}(1^\lambda), \\ (u,s) \leftarrow \mathcal{A}_2(\sigma), \\ (tr, w) \leftarrow \mathcal{E}^\mathcal{O}(\sigma,u) \end{array} \right. \right] \end{array} \right| \ll \mu(\lambda) \] となるような無視できる関数 \(\mu(\lambda)\) が存在し、特定の点に巻き戻してその点以降の検証者に対してフレッシュなランダム性で再開することが可能であるような予期される多項式時間エミュレータ \(\mathcal{E}\) がすべての決定論的多項式時間 \(\mathcal{P}^*\) に対して存在するのであれば、\(({\rm Setup},\mathcal{P},\mathcal{V})\) は証人拡張エミュレーション (witness-extended emulation)を持つ。ここでオラクルは \(\mathcal{O} = \langle \mathcal{P}^*(\sigma,u,s),\mathcal{V}(\sigma,u)\rangle\) によって与えられる。また、非一様な多項式時間の敵対者 \(\mathcal{A}_1\) と \(\mathcal{A}_2\) に限定することで計算論的証人拡張エミュレーションを定義することができる。

我々は、例えば [BCC⁺16] が使用している [GI08b, Lin03] で定義されているような知識の健全性 (knowledge-soundness) を定義するために証人拡張エミュレーションを使用する。非公式には、検証者を満足させるアーギュメントを敵対者がある確率で生成できるときはいつでも、同じ確率で同一に分布するアーギュメントを生成するエミュレータだけでなく証人も存在する。値 \(s\) はランダム性を含んだ \(\mathcal{P}^*\) の内部状態を考えることができる。エミュレータは証明者と検証者の間の対話を任意の位置まで巻き戻し、証明者は同じ内部状態、検証者は新しいランダム性を持った状態で再開することができる。状態 \(s\) の時に \(\mathcal{P}^*\) が説得力のあるアーギュメントを出すときはいつでも \(\mathcal{E}\) は証人を抽出することができ、したがって我々は \((\sigma,u,w) \in \mathcal{R}\) となるような \(w\) の知識のアーギュメントを持つことになる。

定義 11 (公開コイン ; Public Coin). 検証者から証明者に送信されるすべてのメッセージが証明者のメッセージとは独立して一様にランダムに選ばれている場合、つまりチャレンジが検証者のランダム性 \(\rho\) に対応する場合、知識のアーギュメント \(({\rm Setup},\mathcal{P},\mathcal{V})\) は公開コインと呼ばれる。

\((\sigma,x,w)\in\mathcal{R}\) であるという事実から推論できるものを除いて \(w\) に関する情報を漏らさないのであれば知識のアーギュメントはゼロ知識である。我々は特別な正直検証者のゼロ知識 (special honest-verifier zero-knowledge) を持つ知識のアーギュメントを提示する。これは、検証者のチャレンジ値が与えられれば、証人を知らなくてもアーギュメント全体を効率的にシミュレーションすることが可能であることを意味している。

定義 12 (完全で特別な正直検証者のゼロ知識 ;Perfect Special Honest-Verifier Zero-Knowledge). 対話的敵対者 \(\mathcal{A}_1\) と \(\mathcal{A}_2\) のすべてのペアに対して \[ \begin{eqnarray*} & & Pr\left[ (\sigma,u,w) \in \mathcal{R} \ \ \mbox{and} \ \ \mathcal{A}_1(tr) = 1 \left| \begin{array}{l} \sigma \leftarrow {\rm Setup}(1^\lambda), 8u,w,\rho) \leftarrow \mathcal{A}_2(\sigma), \\ tr \leftarrow \langle \mathcal{P}(\sigma,u,w), \mathcal{V}(\sigma,u;\rho) \rangle \end{array} \right. \right] \\ & = & Pr\left[ (\sigma,u,w) \in \mathcal{R} \ \ \mbox{and} \ \ \mathcal{A}_1(tr) = 1 \left| \begin{array}{l} \sigma \leftarrow {\rm Setup}(1^\lambda), (u,w,\rho) \leftarrow \mathcal{A}_2(\sigma), \\ tr \leftarrow \mathcal{S}(u,\rho) \end{array} \right. \right] \end{eqnarray*} \] となるような確率的多項式時間シミュレータ \(\mathcal{S}\) が存在するのであれば、知識の公開コインアーギュメント \(({\rm Setup},\mathcal{P},\mathcal{V})\) は \(\mathcal{R}\) に対する知識の完全で特別な正直検証者ゼロ知識 (SHVZR) アーギュメントである。ここで \(\rho\) は検証者によって使用される公開コインランダム性である。

この定義では敵対者はステートメントと証人に対して分布を選択するが、依然として有効なステートメントと証人に対してはシミュレートされたものと正直に生成された写しを区別することはできない。

ここでレンジプルーフを定義する。レンジプルーフとは、コミットされた値が特定の範囲にあるというコミットメントの開始を証明者が知っている証明である。レンジプルーフは整数のコミットメントが正の値であることや、素数位数の体の元に対する 2 つの準同型コミットメントが加算された時に素数を法としてオーバーフローしないことを示すために使うことができる。

定義 13 (ゼロ知識レンジプルーフ). 全順序 (total ordering) を持つ集合のメッセージ空間 \({\sf M}_{\rm pp}\) におけるコミットメントスキーム \(({\rm Setup},{\rm Com})\) が与えられたとき、ゼロ知識レンジプルーフは関連 \(\mathcal{R}_{\sf Range}\): \[ \mathcal{R}_{\sf Range}: ({\rm pp}, ({\bf com}, l, r), (x, \rho)) \in \mathcal{R}_{\sf Range} \leftrightarrow {\bf com} = {\rm Com}(x; \rho) \wedge l \ll x \lt r \] に対する知識の SHVZK アーギュメントである。

2.4 表記

\(\mathbb{G}\) を素数位数 \(p\) の巡回群、\(\mathbb{Z}_p\) を \(p\) を法とする整数の環とする。\(\mathbb{G}^n\) と \(\mathbb{Z}_p^n\) をそれぞれ \(\mathbb{G}\) と \(\mathbb{Z}_p\) 上の次元 \(n\) のベクトル空間とする。\(\mathbb{Z}_p^*\) を \(\mathbb{Z}_p \backslash\{0\}\) とする。\(\mathcal{G}\) の生成系を \(g,h,v,u \in \mathbb{G}\) と表記する。コミットメントを表す群要素は大文字で表記され、ブラインドファクターはギリシャ文字で表記する。例えば \(C=g^\alpha h^\alpha \in \mathbb{G}\) は \(a\) に対する Pedersen コミットメントである。文脈から明らかではない場合 \(x,y,z \in \mathbb{Z}_p^*\) は一様分布のチャンレジである。\(\mathbb{Z}_p^*\) からの要素の一様サンプリングを \(x \stackrel{$}{\leftarrow} \mathbb{Z}_p^*\) と表記する。本稿では次のように定義されたベクトル表記も使用する。ボルドーフォントはベクトルを示す。例えば \(\vector{A} \in \mathbb{F}^{n\times m}\) は \(a_{i,j}\) が \(\vector{A}\) の \(i\) 行目と \(j\) 列目にあるような \(n\) 行 \(m\) 列の行列である。スカラー \(c \in \mathbb{Z}_p\) とベクトル \(\vector{a} \in \mathbb{Z}_p^n\) に対して、\(b_i = c \cdot a_i\) となるベクトルを \(\vector{b} = c\cdot\vector{a} \in \mathbb{Z}_p^n\) と表記する。さらに \(\langle\vector{a},\vector{b}\rangle=\sum_{i=1}^n a_i\cdot b_i\) を 2 つのベクトル \(\vector{a}, \vector{b} \in \mathbb{F}^n\) の内積とし、\(\vector{a} \circ \vector{b} = (a_1\cdot b_1,\ldots,a_n \cdot b_n) \in \mathbb{F}^n\) を 2 つのベクトルのアダマール積またはエントリごとの乗算とする。

我々はまた各コヒーレント \(\vector{p_i}\) が \(\mathbb{Z}_p^n\) のベクトルであるようなベクトル多項式 \(p(X) = \sum_{i=0}^d \vector{p_i} \cdot X^i \in \mathbb{Z}_p^n[X]\) を定義する。2 つのベクトル多項式 \(l(X)\), \(r(X)\) 間の内積は \[ \begin{equation} \langle l(X), r(X) \rangle = \sum_{i=0}^d \sum_{j=0}^i \langle \vector{l_i}, \vector{r_i} \rangle \cdot X^{i+j} \in \mathbb{Z}_p{X} \end{equation} \] と定義される。\(t(X)=\langle\vector{l}(X),\vector{r}(X)\rangle\) とすると、内積はすべての \(x \in \mathbb{Z}_p\) に対して \(t(x) = \langle l(x), r(x) \rangle\) を保持するように定義される。つまり \(x\) で多項式を評価して内積を得ることは、\(x\) で内積多項式を評価することと同じである。

ベクトル \(\vector{g}=(g_i,\ldots,g_n) \in \mathbb{G}^n\) と \(\vector{a} \in \mathbb{Z}_p^n\) に対して \(C = \vector{g}^\vector{a} = \prod_{i=1}^n g_i^{a_i} \in \mathbb{G}\) と書く。この量はベクトル \(\vector{a}\in\mathbb{Z}_p^n\) に対する束縛 (秘匿ではない) コミットメントである。そのようなコミットメント \(C\) と非ゼロのエントリを持つベクトル \(\vector{b} \in \mathbb{Z}_p^n\) が与えられると \(C\) を \(\vector{a} \circ \vector{b}\) への新しいコミットメントとして扱うことができる。そのためには \(C=\prod_{i=1}-n(g'_i)^{a_i \cdot b_i}\) となるような \(g'_a = g_i^{b_i^{-1}}\) を定義する。この新しいコミットメントの束縛特性は古いコミットメントから継承されている。

2 つのベクトルの連結を \(\vector{a} || \vector{b}\) とする: \(\vector{a} \in \mathbb{Z}_p^n\) と \(\vector{b} \in \mathbb{Z}_p^m\) であれば \(\vector{a} || \vector{b} \in \mathbb{Z}_p^{n+m}\) である。\(0 \ll \ell \ll n\) に対してベクトルのスライスを表記するために Python 表記を使用する: \[ a_{[:\ell]} = (a_1,\ldots,a_\ell) \in \mathbb{F}^\ell, \ \ \ \ a_{[\ell:]} = (a_{\ell+1},\ldots,n) \in \mathbb{F}^{n-l} \] \(k \in \mathbb{Z}_p^*\) に対して \(k\) の最初の \(n\) 乗を含むベクトルを表すために \(\vector{k}^n\) を使用する。つまり \[ \vector{k}^n = (1, k, k^2, \ldots, k^{n-1}) \in (\mathbb{Z}_p^*)^n \] 例えば \(\vector{2}^n = (1,2,4,\ldots,2^{n-1})\)。\(\vector{k}^{-n} = (\vector{k}^\vector{-1})^n = (1,k^{-1},\ldots,k^{-n+1})\) 等価。

最後に、我々は指定された Public Input と Witness を用いた関連 Relation を表記するのに \(\{(\mbox{Public Input}; \mbox{Witness}): \mbox{Relation}\}\) とする。

3 Improved Inner-Product Argument

3.1 Inner-Product Verification through Multi-Exponentation

4 Range Proof Protocol with Logarithmic Size

4.1 Inner-Product Range Proof

4.2 Logarithmic Range Proof

4.3 Aggregating Logarithmic Proofs

4.4 Non-Interactive Proof through Fiat-Shamir

4.5 A Simple MPC Protocol for Bulletproofs

4.6 Perfect Binding Commitments and Proofs

5 Zero-Knowledge Proof for Arithmetic Circuits

5.1 Inner-Product Proof for Arithmetic Circuits

5.2 Logarithmic-Sized Protocol

6 パフォーマンス

6.1 理論パフォーマンス

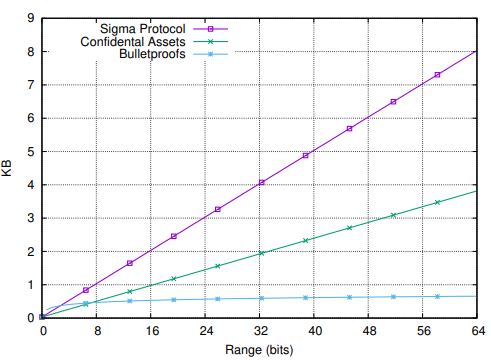
Table 1 に様々なレンジプルーフプロトコルにおける証明サイズの分析的測定値を示す。単一の証明と範囲 \([0,2^n-1]\) の \(m\) 個の証明の両方の証明サイズを比較する。我々は Bulletproofs を [PBF⁺] と、各ビットに対してコミットしコミットが 0 または 1 であることを示す証明である \(\Sigma\) プロトコルと比較する。表は複数のレンジプルーフを一度に提供する場合に Bulletproofs が有意に有利であることを示している。セクション 4.3 で示したプロトコルの証明サイズは \(m\) 個のレンジプルーフを実行する場合には加算対数ファクターでしか成長しないが、他のすべての方法は \(m\) に乗数的に成長する。

Table 1: \(m\) 個の証明に対するレンジプルーフのサイズ。\(m=1\) は単一のレンジプルーフの特殊なケースである。
# \(\mathbb{G}\) elements # \(\mathbb{Z}_p\) elements
\(\Sigma\) Protocol [CD98] \(mn\) \(3mn+1\)
Poelstra et al. [PBF⁺] \(0.63 \cdot mn\) \(1.26 \cdot mn + 1\)
Bulletproofs \(2\left(\log_2(n) + \log_2(m)\right) + 4\) \(5\)

6.2 多重指数化とバッチ検証を用いた検証者の最適化

セクション 1.2 で論議したアプリケーションの多くでは検証者の実行時間が特に重要である。例えば機密トランザクションについては各フルノードは機密トランザクションと関連するレンジプルーフをすべてチェックする必要がある。そこで我々は非対話的検証者のための最適化をいくつか紹介する。我々は単一のレンジプルーフに対する最適化を提示するが、それらはすべて集約レンジプルーフと演算回路プロトコルにも適用される。

単一の多重指数化 (single multi-exponentiation). セクション 3.1 では内積の検証が単一の多重指数化に削減できることを示した。この考えからさらに、サイズ \(2n+2\log_2(n)+7\) の単一の多重指数化を使用してレンジプルーフ全体を検証するために拡張することができる。Bulletproofs の検証者は (68) と (16) の 2 つのチェックのみを実行していることに注意。このアイディアはこれらのチェックが実際に実行されるまで指数計算を遅らせ、それらを単一のチェックに連結することである。したがってセクション 3.1 で議論したようにレンジプルーフからの入力を使用して内積アーギュメントを展開する。結果として得られたプロトコルを以下に示す。\(x_u\) はプロトコル 1 からのチャレンジであり \(x_j\) はプロトコル 2 のラウンド \(j\) からのチャレンジである。\(L_j\) と \(R_j\) はプロトコル 2 のラウンド \(j\) からの \(L\), \(R\) 値である。検証者は以下の検証手順を実行する:

乱数 \(c \stackrel{$}{\rightarrow} \mathbb{Z}_p\) を使用することで (98) と (105) の 2 つの多重指数化を結合することができる。これは、もし乱数 \(c\) に対して \(A^cB=1\) であれば高い確率で \(A=1 \wedge B=1\) である。

多重指数化 (105) と (98) を効率的に計算するための様々なアルゴリズムが知られている。[BDLO12] で説明されているように、Pippenger の [Pip80] のようなアルゴリズムは \(O\frac{n}{\log(n)}\) でスケールする群演算、すなはち劣線形に実行される。現実的に問題なサイズではこれらの演算が検証時間を支配している。

スカラー計算. さらなる最適化は \(l_i\) と \(r_i\) 値の計算に関係する。すべての \(i\) に対して \(x^{(i)}=\prod_{j=1}^{\log_2 n} x_j^{b(i,j)}\) を計算する代わりに、バッチ除算を適用することで \(\mathbb{Z}_p\) の 1 回の乗算のみを使用して各チャレンジ積を計算することができる。まず単一の反転を用いて最初のチャレンジを得るために \(x^{(1)}=(\prod_{j=1}^{\log_2 n} x_j)^{-1}\) を計算する。それから \(x^{(2)}=x^{(1)}x_1^2\), \(x^3=x^{(1)}x_2^2\), そして例えば \(x^{(7)}=x^{(3)}x_5^2\) を計算する。一般的に、\(x^{(i)}\) を計算するには \(k\) を \(i-1\) の 2 の次に低い累乗とし、\(\mathbb{Z}_p\) での一つの追加の乗算のみを取り反転を行わない \(x^{(i)} = x^{(i-k)} \cdot x_{k+1}^2\) を計算する。さらに式 (105) をチェックするためにどのみちチャレンジの 2 乗が計算されることに注意。

バッチ検証. さらに重要な最適化は複数の証明の検証に関することである。セクション 1.2 で論議した多くのアプリケーションでは、検証者は一度に複数の (別々の) レンジプルーフを検証する必要がある。例えばトランザクションのブロックを受信しているビットコインのノードはすべてのトランザクション、すなはちレンジプルーフを並列で検証する必要がある。前述のように検証は大規模な多重指数化に集約される。事実、生成系の \(2n+2\) は公開パラメータのみに依存し、\(2 \log(n)+5\) のみが証明に依存する。したがって我々は高価なべき乗の回数を減らすためにバッチ検証 [BGR98] を適用することができる。バッチ検証は、\(g^x = 1 \wedge g^y = 1\) をチェックすることが十分な大きさのドメインからランダムなスカラー \(\alpha\) を描画し、\(g^{\alpha\cdot x + y} = 1\) をチェックすることでチェックされることができるという観測に基づいている。後者の式は高い確率で \(g^x = 1 \wedge g^y = 1\) を意味するが後者のほうが効率的にチェックできる。同じトリックが多重指数化に適用され追加の証明ごとに \(2n\) のべき乗を節約することができる。これは底が同等であるという違いはあるが複数のべき乗を 1 つに結合するために使うトリックと同等である。サイズ \(n\) の \(m\) 個の異なるレンジプルーフを検証するには \(O(m\cdot n)\) スカラー演算とともにサイズ \(2n + 2 + m \cdot (2 \cdot \log(n) + 5)\) の単一の多重指数化のみを必要とする。

同じ公開パラメータを使用しているのであれば、この最適化は回路や異なる回路の証明にも適用できることに注意。

単一の検証に対してであっても、ほとんどの生成系が公開パラメータで固定されているという事実を利用できる。検証者と証明車の両方が事前計算 [Gor98] を使った高速の固定ベースのべき乗を使用してすべての多重指数化を高速化できる。

6.3 実装とパフォーマンス

実際に Bulletproofs のパフォーマンスを評価するために我々は C でのリファレンス実装を提供し、多くの暗号通貨クライアントで使用されている一般的なライブラリ libsecp256k1 に統合する。libsecp256k1 は 128 ビットセキュリティの楕円曲線 secp256k12 を使用する。

圧縮された形では secp256k1 の点は 32 バイト + 1 ビットて保存することができる。生成系の事前計算を除いて前述のすべての最適化を使用する。証明者は \(\vector{l}\) と \(\vector{r}\) の計算までに定数演算時間を使用する。定理 2 により内積アーギュメントは \(\vector{l}\) と \(\vector{r}\) を秘匿する必要がないため、可変時間演算を使用することができる。検証者は秘密を持たないため多重指数化のように安全に可変時間演算を使用することができる。

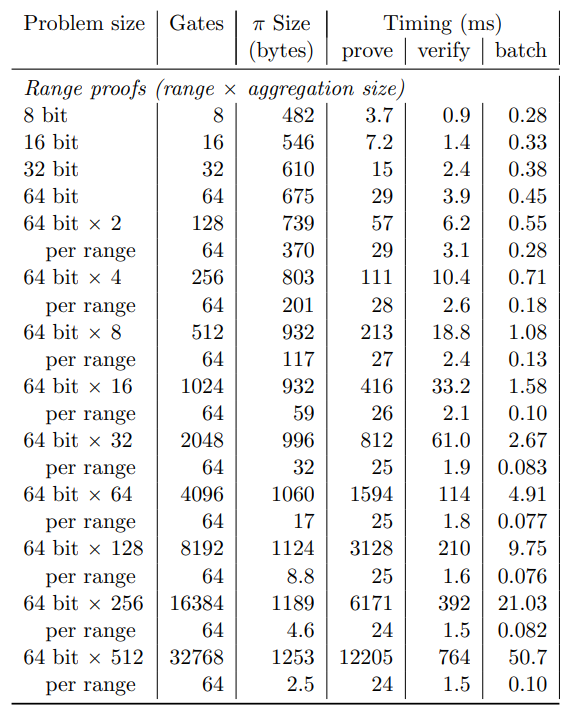
すべての実験は 2.00GHz にスロットルされた Intel i7-6820HQ システムでシングルスレッドを使用して実行された。すべての実験で 100MB 未満のメモリを使用した。参考までに、このシステムで ECDSA 署名の検証は 86μs を要する。Table 2 は証明サイズの点で [PBF⁺] での 3.8kB 証明サイズよりも Bulletproofs のほうが大幅に改善されていることを示している。単一の 64 ビットレンジプルーフは 688 バイトである。[PBF⁺] の 32 個の証明では 121kB を消費していたのに対して 32 個のレンジを集約した証明はわずか 1kB となる。単一の 64 ビットレンジプルーフを検証するためのコストは 3.9ms だが、多数の証明をバッチ検証することで償却コストを 450 マイクロ秒または 5.2 ECDSA 検証に抑えることができる。64 レンジの集約証明の検証にはレンジごとに 61 ミリ秒または 1.9 ミリ秒かかる。追加の証明の検証にかかる限界コストは 1 レンジあたり 2.67 ミリ秒または 83 マイクロ秒であり、このようなバッチ検証の恩恵を受けない ECDSA 署名の検証よりも少ない。

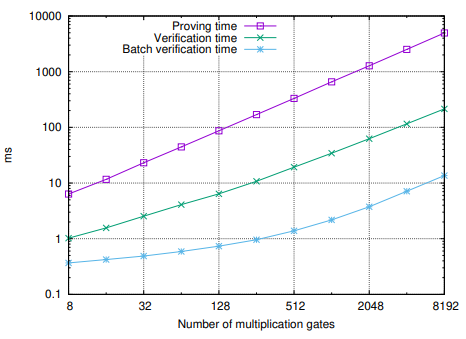
将来の Bulletproofs の利用を支援するっために算術回路用のプロトコル 3 も実装し、Pinocchio [PHGR13] フォーマットの回路に対する Bulletproofs フォーマットへのパーサを提供した。これは C のサブセットから回路フォーマットへのコンパイラを含む Pinocchio ツールチェーンに Bulletproofs をフックする。実装を評価するためにハッシュ原像に対するいくつかの回路を Table 3 と Figure 3 で分析する。

具体的には jsnark3 によってい生成された SHA256 回路と、Jubjub4 に似た埋め込み楕円曲線上の Pedersen ハッシュ関数がベンチマークされる。384 ビットの Pedersen ハッシュ原像を知るための Bulletproofs は約 1kB で検証に 61ms がかかる。SHA256 原像証明は 1.4kB で検証に 750ms かかる。追加の証明を検証する限界コストは 41.5ms である。Figure 3 は証明と検証時間が線形に伸びていることを表している。バッチ検証は最初対数的に成長し、その後線形に成長する。小さな回路では指数演算の対数的回数がコストを支配するが、大きな回路の場合は線形スカラー演算が支配する。

Figure 1. レンジプルーフのサイズ
Figure 2. レンジプルーフの時間
Figure 3. 算術回路の時間 (Pedersen Hash)
Table 2. レンジプルーフ: 性能と証明サイズ

Acknowledgements

We thank Shashank Agrawal for coming up with the Bulletproof name (short like a bullet with bulletproof security assumptions). We thank Peter Dettman for pointing out the batch inversion trick. We thank Sean Bowe and Daira Hopwood for various optimizations applicable to arithmetic circuits for Pedersen hash functions. Further we thank Philip Hayes, Cathie Yun and the anonymous reviewers for helpful corrections. This work was supported by NSF, DARPA, a grant from ONR, and the Simons Foundation.

References

  1. [AHIV17] Scott Ames, Carmit Hazay, Yuval Ishai, and Muthuramakrishnan Venkitasubramaniam. Ligero: Lightweight sublinear arguments without a trusted setup. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pages 2087–2104. ACM, 2017.
  2. [AKR⁺13] Elli Androulaki, Ghassan O Karame, Marc Roeschlin, Tobias Scherer, and Srdjan Capkun. Evaluating User Privacy in Bitcoin. In Financial Cryptography, 2013.
  3. [And17] Oleg Andreev. Hidden in Plain Sight: Transacting Privately on a Blockchain. blog. chain.com, 2017.
  4. [BB04] Dan Boneh and Xavier Boyen. Short signatures without random oracles. In Advances in Cryptology - EUROCRYPT 2004, pages 56–73, 2004.
  5. [BBB⁺18] Benedikt Bünz, Jonathan Bootle, Dan Boneh, Andrew Poelstra, Pieter Wuille, and Greg Maxwell. Bulletproofs: Short proofs for confidential transactions and more (conference version). In Security and Privacy (SP), 2018 IEEE Symposium on, pages 319–338. IEEE, 2018.
  6. [BCC⁺16] Jonathan Bootle, Andrea Cerulli, Pyrros Chaidos, Jens Groth, and Christophe Petit. Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 327–357. Springer, 2016.
  7. [BCCT12] Nir Bitansky, Ran Canetti, Alessandro Chiesa, and Eran Tromer. From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again. In Innovations in Theoretical Computer Science 2012, pages 326–349, 2012.
  8. [BCCT13] Nir Bitansky, Ran Canetti, Alessandro Chiesa, and Eran Tromer. Recursive composition and bootstrapping for SNARKS and proof-carrying data. In Symposium on Theory of Computing Conference, STOC’13, Palo Alto, CA, USA, June 1-4, 2013, pages 111–120, 2013.
  9. [BCG⁺17a] Eli Ben-Sasson, Alessandro Chiesa, Ariel Gabizon, Michael Riabzev, and Nicholas Spooner. Interactive oracle proofs with constant rate and query complexity. In 44th International Colloquium on Automata, Languages, and Programming, ICALP 2017, July 10-14, 2017, Warsaw, Poland, pages 40:1–40:15, 2017.
  10. [BCG⁺17b] Jonathan Bootle, Andrea Cerulli, Essam Ghadafi, Jens Groth, Mohammad Hajiabadi, and Sune K. Jakobsen. Linear-time zero-knowledge proofs for arithmetic circuit satisfiability. Cryptology ePrint Archive, Report 2017/872, 2017. http://eprint.iacr.org/2017/872.
  11. [BDLO12] Daniel J Bernstein, Jeroen Doumen, Tanja Lange, and Jan-Jaap Oosterwijk. Faster batch forgery identification. In International Conference on Cryptology in India, pages 454–473. Springer, 2012.
  12. [BdM93] Josh Cohen Benaloh and Michael de Mare. One-way accumulators: A decentralized alternative to digital sinatures (extended abstract). In Advances in Cryptology - EUROCRYPT ’93, pages 274–285, 1993.
  13. [BG12] Stephanie Bayer and Jens Groth. Efficient zero-knowledge argument for correctness of a shuffle. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 263–280. Springer, 2012.
  14. [BGB17] Benedikt Bünz, Steven Goldfeder, and Joseph Bonneau. Proofs-of-delay and randomness beacons in ethereum. IEEE SECURITY and PRIVACY ON THE BLOCKCHAIN (IEEE S&B), 2017.
  15. [BGG17] Sean Bowe, Ariel Gabizon, and Matthew D. Green. A multi-party protocol for constructing the public parameters of the pinocchio zk-snark. IACR Cryptology ePrint Archive, 2017:602, 2017.
  16. [BGR98] Mihir Bellare, Juan A. Garay, and Tal Rabin. Fast batch verification for modular exponentiation and digital signatures. In Kaisa Nyberg, editor, Advances in Cryptology — EUROCRYPT’98, pages 236–250, Berlin, Heidelberg, 1998. Springer Berlin Heidelberg.
  17. [BLS01] Dan Boneh, Ben Lynn, and Hovav Shacham. Short signatures from the weil pairing. In International Conference on the Theory and Application of Cryptology and Information Security, pages 514–532. Springer, 2001.
  18. [BMC⁺15] Joseph Bonneau, Andrew Miller, Jeremy Clark, Arvind Narayanan, Joshua A. Kroll, and Edward W. Felten. Research Perspectives and Challenges for Bitcoin and Cryptocurrencies. IEEE Symposium on Security and Privacy, 2015.
  19. [BR93] Mihir Bellare and Phillip Rogaway. Random oracles are practical: A paradigm for designing efficient protocols. In CCS ’93, pages 62–73, 1993.
  20. [BSBC⁺17] Eli Ben-Sasson, Iddo Bentov, Alessandro Chiesa, Ariel Gabizon, Daniel Genkin, Matan Hamilis, Evgenya Pergament, Michael Riabzev, Mark Silberstein, Eran Tromer, et al. Computational integrity with a public random string from quasilinear pcps. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 551–579. Springer, 2017.
  21. [BSBTHR18] Eli Ben-Sasson, Iddo Ben-Tov, Yinon Horesh, and Michael Riabzev. Scalable, transparent, and post-quantum secure computational integrity. https://eprint.iacr.org/2018/046.pdf, 2018.
  22. [BSCG⁺13] Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin, Eran Tromer, and Madars Virza. SNARKs for C: Verifying program executions succinctly and in zero knowledge. In CRYPTO, 2013.
  23. [BSCG⁺14] Eli Ben-Sasson, Alessandro Chiesa, Christina Garman, Matthew Green, Ian Miers, Eran Tromer, and Madars Virza. Zerocash: Decentralized anonymous payments from Bitcoin. In IEEE Symposium on Security and Privacy. IEEE, 2014.
  24. [CCs08] Jan Camenisch, Rafik Chaabouni, and abhi shelat. Efficient protocols for set membership and range proofs. Advances in Cryptology-ASIACRYPT 2008, pages 234–252, 2008.
  25. [CD98] Ronald Cramer and Ivan Damgård. Zero-knowledge proofs for finite field arithmetic, or: Can zero-knowledge be for free? In CRYPTO 98, pages 424–441. Springer, 1998.
  26. [CGGN17] Matteo Campanelli, Rosario Gennaro, Steven Goldfeder, and Luca Nizzardo. Zeroknowledge contingent payments revisited: Attacks and payments for services. Commun. ACM, 2017.
  27. [Cha82] David Chaum. Blind signatures for untraceable payments. In CRYPTO, 1982.
  28. [CHL05] Jan Camenisch, Susan Hohenberger, and Anna Lysyanskaya. Compact e-cash. In EUROCRYPT, 2005.
  29. [CLas10] Rafik Chaabouni, Helger Lipmaa, and abhi shelat. Additive combinatorics and discrete logarithm based range protocols. In Information Security and Privacy - 15th Australasian Conference, ACISP 2010, Sydney, Australia, July 5-7, 2010. Proceedings, pages 336–351, 2010.
  30. [CRR11] Ran Canetti, Ben Riva, and Guy N Rothblum. Practical delegation of computation using multiple servers. In Proceedings of the 18th ACM conference on Computer and communications security, pages 445–454. ACM, 2011.
  31. [DBB⁺15] G Dagher, B Bünz, Joseph Bonneau, Jeremy Clark, and D Boneh. Provisions: Privacy-preserving proofs of solvency for bitcoin exchanges (full version). Technical report, IACR Cryptology ePrint Archive, 2015.
  32. [FS01] Jun Furukawa and Kazue Sako. An efficient scheme for proving a shuffle. In Crypto, volume 1, pages 368–387. Springer, 2001.
  33. [GGPR13] Rosario Gennaro, Craig Gentry, Bryan Parno, and Mariana Raykova. Quadratic span programs and succinct nizks without pcps. In Advances in Cryptology - EUROCRYPT 2013, pages 626–645, 2013.
  34. [GH98] Oded Goldreich and Johan Håstad. On the complexity of interactive proofs with bounded communication. Inf. Process. Lett., 67(4):205–214, 1998.
  35. [GI08a] Jens Groth and Yuval Ishai. Sub-linear zero-knowledge argument for correctness of a shuffle. Advances in Cryptology–EUROCRYPT 2008, pages 379–396, 2008.
  36. [GI08b] Jens Groth and Yuval Ishai. Sub-linear zero-knowledge argument for correctness of a shuffle. In Advances in Cryptology - EUROCRYPT 2008, pages 379–396, 2008.
  37. [GKR08] Shafi Goldwasser, Yael Tauman Kalai, and Guy N Rothblum. Delegating computation: interactive proofs for muggles. In Proceedings of the fortieth annual ACM symposium on Theory of computing, pages 113–122. ACM, 2008.
  38. [Gor98] Daniel M Gordon. A survey of fast exponentiation methods. Journal of algorithms, 27(1):129–146, 1998.
  39. [Gro03] Jens Groth. A verifiable secret shuffle of homomorphic encryptions. In Public Key Cryptography, volume 2567, pages 145–160. Springer, 2003.
  40. [Gro05] Jens Groth. Non-interactive zero-knowledge arguments for voting. In International Conference on Applied Cryptography and Network Security, pages 467–482. Springer, 2005.
  41. [Gro10] Jens Groth. Short pairing-based non-interactive zero-knowledge arguments. In Advances in Cryptology - ASIACRYPT 2010, pages 321–340, 2010.
  42. [Gro16] Jens Groth. On the size of pairing-based non-interactive arguments. In Advances in Cryptology - EUROCRYPT 2016, pages 305–326, 2016.
  43. [GS08] Jens Groth and Amit Sahai. Efficient non-interactive proof systems for bilinear groups. In Advances in Cryptology - EUROCRYPT 2008, pages 415–432, 2008.
  44. [GVW02] Oded Goldreich, Salil P. Vadhan, and Avi Wigderson. On interactive proofs with a laconic prover. Computational Complexity, 11(1-2):1–53, 2002.
  45. [Jed16] TE Jedusor. Mimblewimble, 2016.
  46. [KMS⁺16] Ahmed Kosba, Andrew Miller, Elaine Shi, Zikai Wen, and Charalampos Papamanthou. Hawk: The blockchain model of cryptography and privacy-preserving smart contracts. In Security and Privacy (SP), 2016 IEEE Symposium on, pages 839–858. IEEE, 2016.
  47. [KP95] Joe Kilian and Erez Petrank. An efficient non-interactive zero-knowledge proof system for NP with general assumptions. Electronic Colloquium on Computational Complexity (ECCC), 2(38), 1995.
  48. [Lin03] Yehuda Lindell. Parallel coin-tossing and constant-round secure two-party computation. J. Cryptology, 16(3):143–184, 2003.
  49. [Lip03] Helger Lipmaa. On diophantine complexity and statistical zero-knowledge arguments. In International Conference on the Theory and Application of Cryptology and Information Security, pages 398–415. Springer, 2003.
  50. [Max] G Maxwell. Zero knowledge contingent payment. 2011. URl: https://en.bitcoin.it/wiki/Zero_Knowledge_Contingent_Payment (visited on 05/01/2016).
  51. [Max13] Gregory Maxwell. CoinJoin: Bitcoin privacy for the real world. bitcointalk.org, August 2013.
  52. [Max16] Greg Maxwell. Confidential transactions. https://people.xiph.org/~greg/confidential_values.txt, 2016.
  53. [Mic94] Silvio Micali. Cs proofs. In Foundations of Computer Science, 1994 Proceedings., 35th Annual Symposium on, pages 436–453. IEEE, 1994.
  54. [Mon] Monero - Private Digital Currency . https://getmonero.org/.
  55. [MP15] Gregory Maxwell and Andrew Poelstra. Borromean ring signatures. http://diyhpl.us/~bryan/papers2/bitcoin/Borromean%20ring%20signatures.pdf, 2015.
  56. [MPJ⁺13] Sarah Meiklejohn, Marjori Pomarole, Grant Jordan, Kirill Levchenko, Damon McCoy, Geoffrey M Voelker, and Stefan Savage. A fistful of bitcoins: characterizing payments among men with no names. In IMC, 2013.
  57. [MSH17] Patrick McCorry, Siamak F Shahandashti, and Feng Hao. A smart contract for boardroom voting with maximum voter privacy. IACR Cryptology ePrint Archive, 2017:110, 2017.
  58. [Nak08] S Nakamoto. Bitcoin: A peer-to-peer electionic cash system. Unpublished, 2008.
  59. [Nef01] C Andrew Neff. A verifiable secret shuffle and its application to e-voting. In Proceedings of the 8th ACM conference on Computer and Communications Security, pages 116–125. ACM, 2001.
  60. [NM⁺16] Shen Noether, Adam Mackenzie, et al. Ring confidential transactions. Ledger, 1:1–18, 2016.
  61. [P⁺91] Torben P Pedersen et al. Non-interactive and information-theoretic secure verifiable secret sharing. In Crypto, volume 91, pages 129–140. Springer, 1991.
  62. [PBF⁺] Andrew Poelstra, Adam Back, Mark Friedenbach, Gregory Maxwell, and Pieter Wuille. Confidential assets.
  63. [PHGR13] Bryan Parno, Jon Howell, Craig Gentry, and Mariana Raykova. Pinocchio: Nearly practical verifiable computation. In Security and Privacy (SP), 2013 IEEE Symposium on, pages 238–252. IEEE, 2013.
  64. [PHGR16] Bryan Parno, Jon Howell, Craig Gentry, and Mariana Raykova. Pinocchio: nearly practical verifiable computation. Commun. ACM, 59(2):103–112, 2016.
  65. [Pip80] Nicholas Pippenger. On the evaluation of powers and monomials. SIAM Journal on Computing, 9:230–250, 1980.
  66. [Poe] Andrew Poelstra. Mimblewimble.
  67. [RM] Tim Ruffing and Giulio Malavolta. Switch commitments: A safety switch for confidential transactions.
  68. [RMSK14] Tim Ruffing, Pedro Moreno-Sanchez, and Aniket Kate. CoinShuffle: Practical decentralized coin mixing for Bitcoin. In ESORICS, 2014.
  69. [San99] Tomas Sander. Efficient accumulators without trapdoor extended abstract. Information and Communication Security, pages 252–262, 1999.
  70. [TR] Jason Teutsch and Christian Reitwießner. A scalable verification solution for blockchains.
  71. [vS13] Nicolas van Saberhagen. Cryptonote v 2. 0, 2013.
  72. [Woo14] Gavin Wood. Ethereum: A secure decentralized transaction ledger. http://gavwood.com/paper.pdf, 2014.
  73. [WTs⁺] Riad S Wahby, Ioanna Tzialla, abhi shelat, Justin Thaler, and Michael Walfish. Doubly-efficient zksnarks without trusted setup.

A A General Forking Lemma

(省略)

B Proof of Theorem 1

(省略)

C Proof of Theorem 3

(省略)

D Proof of Theorem 4

(省略)

翻訳抄

高速でデータサイズの小さいレンジプルーフ (範囲証明) のゼロ知識証明である Bulletproofs に関する 2018 年の論文。

  1. Benedikt Bunz, Jonathan Bootle, Dan Boneh, Andrew Poelstra, Pieter Wuille, and Gregory Maxwell. Bulletproofs: Short proofs for confidential transactions and more. In 2018 IEEE Symposium on Security and Privacy, SP 2018, Proceedings, 21-23 May 2018, San Francisco, California, USA.