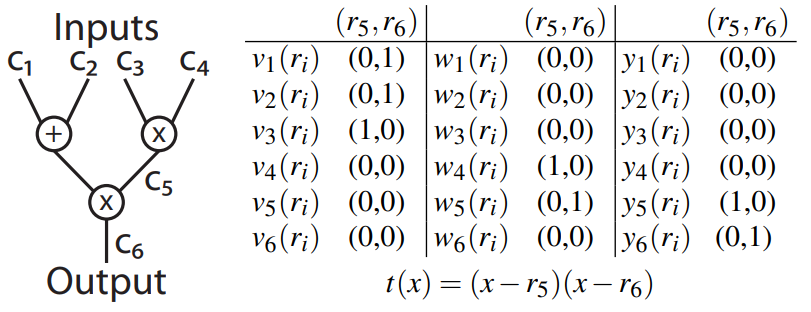セキュリティ

論文翻訳: Pinocchio: Nearly Practical Verifiable Computation

Takami Torao 2013年の論文 #zk-SNARK #Pinocchio
  • このエントリーをはてなブックマークに追加
Bryan Parno
Jon Howell
Microsoft Research
Graig Gentry
Mariana Raykova
IBM Research

Abstract

クラウドにアウトソースされた計算の信頼性を高めるに、クライアントは返された結果の正当性を検証できるべきである。我々はこの目的のために、暗号的仮定のみに依存ながら一般的な計算を効率的に検証するために構築されたシステムである Pinocchio を導入する。Pinocchio を使用することで、クライアントは自身の計算を記述する公開評価鍵 (public evaluation key) を作成する; この設定は計算を 1 回評価するごとに行われる。次に、ワーカーは特定の入力に対する計算を評価し、その評価鍵を使用して正当性の証明を作成する。この署名は、実行される計算や入出力のサイズに関係なくわずか 288 バイトである。誰でも公開検証鍵を使用して証明を確認することができる。

重要なことに、7 つのアプリケーションに対する評価は Pinocchio が実際に効率的であることを示している。Pinocchio の検証時間は通常 10ms であり、過去の研究よりも 5〜7 桁短い。実際、Pinocchio は (一部のアプリに対する) ネイティブ実行よりも低コストで検証を実証した最初の汎用システムである。pinocchio はまたワーカーの証明作業をさらに 19〜60 倍削減する。付加的な特徴として Pinocchio は基本プロトコルに無視できるコストを追加してコストでゼロ知識証明に一般化する。最後に、開発を支援するために、Pinocchio は検証可能な計算プロトコルを実装するプログラムに C のサブセットをコンパイルする End-to-End のツールチェーンを提供する。

Table of Contents

  1. Abstract
  2. 1 導入
  3. 2 背景
    1. 2.1 検証可能計算 (VC)
    2. 2.2 二次プログラム
      1. 2.2.1 算術回路と QAPs
      2. 2.2.2 論理回路と QSPs
    3. 2.3 二次プログラムからの VC の構築
  4. 3 理論的改良 [under construction]
    1. 3.1 Our New VC Protocol
  5. 4 Implementation
    1. 4.1 Compiler Toolchain
    2. 4.2 Quadratic Programs and Cryptographic Protocol
      1. 4.2.1 Optimizing Operations
    3. 4.3 Applications
  6. 5 Evaluation
    1. 5.1 Microbenchmarks
    2. 5.2 Comparison With Previous Work
    3. 5.3 End-to-End Application Performance
    4. 5.4 Impact of Our Optimizations
    5. 5.5 QSPs versus QAPs
  7. 6 Related Work
  8. 7 Conclusion and Future Work
  9. Acknowledgements
  10. References
  11. A Cryptographic Assumptions
  12. B Security Proof for Our VC Scheme
  13. 翻訳抄

1 導入

多くの場合、(特にモバイルか機器向け) 計算能力は非対称であるため、比較的弱いクライアントは 1 つ以上の強力なワーカーに計算をアウトソースすることを望むかも知れない。一般的な例としてはクラウドコンピューティングやグリッドコンピューティング、ボランティアによる分散コンピューティング [1] などがある。クライアントはこれらの全ての構成で返された結果を検証し、悪意や誤動作のあるワーカーから保護する必要がある。正当なワーカーの観点からも、検証可能な結果はより高い価値を要求する可能性が高いため有益である。またワーカーは責任を放棄することができる。。望ましくない出力はクライアントが提供したデータの結果であることを証明することができる。

計算の検証問題については多くのシステムや理論研究が行われてきた。(§6) しかしこれらの研究のほとんどは特定の機能に特化しているか、避けがたい仮定に依存しているか、単純に基本的な実用性要件を満たしていなかった。関数固有のソリューション [2, 3, 4, 5, 6] は多くの場合に効率的だが狭いクラスの計算に対してのみ有効である。例えばレプリケーション [1, 7, 8] に基づくシステムでは相関のない障害のみを想定しているが、Trusted Computing [9, 10, 11] またはその他のセキュアなハードウェア [12, 13, 14, 15] は物理的な保護を無効にすることはできないと想定している。最後に、理論コミュニティは魅力的な漸近性を提供する多くの美しい汎用プロトコル [16, 17, 18, 19, 20, 21, 22, 23] を生み出した。しかし、実際には複雑な確率的検証可能証明 (Probabilistically Checkable Proofs) (PCPs) [17] や完全準同形暗号 (fully-homomorphic encryption) (FHE) [24] に依存しているためパフォーマンスは許容できず、小さなインスタンスの検証には数百～数兆年 (§5.2) がかかる。ごく最近の研究 [25, 26, 27, 28] によりこれらのプロトコルは大幅に改善されたが、効率性にはまだ問題がありプロトコルには公開検証などの機能がない。

対照的に、我々は暗号論的仮定のみを行いながら一般的な計算を効率的に検証する具体的なシステムである Pinocchio に付いて説明する。特に Pinocchio は信頼できないワーカーが計算の署名を作成できるような公開検証可能計算 (public verifieable computation) [22, 29] をサポートしている。最初にクライアントは関数を選択し、公開評価鍵と (小さな) 公開検証鍵を生成する。ワーカーは評価鍵が与えられると入力を選択 (またはクライアントが提供するものを検証可能に使用) し、結果に付随する証明 (または署名) を生成することができる。これにより、(クライアントだけではなく) 誰でも検証鍵を使用して、使用した特定の入力に対するワーカーの結果の正確性を確認することができる。追加機能として Pinocchio はゼロ知識検証可能な計算 (zero-knowledge verifiable computation) をサポートする。これによりワーカーは入力に関する情報を一切公開せずに特定のプロパティを持つ入力を知っていることをクライアントに確信させることができる。

Pinocchio の漸近性 (asymptotics) は優れている。鍵の設定と証明の生成には、元の計算のサイズに比例する暗号的努力が必要であり、検証には入力と出力のサイズに対して線形の時間が必要である。さらに驚くべきことに、実行される計算に関係なく Pinocchio の証明は一定のサイズである。重要なこととして、我々の評価 (§5) はこの漸近性に小さな定数が付属していることを示しており、Pinocchio が様々なアプリケーションで実用に近いものとなっていることを示している。

過去の研究と比較すると、Pinocchio は検証時間を 5～7 桁改善し、ほとんどの構成で 10 ミリ秒未満で済み、一部のアプリでネイティブ C 実行を上回ることができる。また過去の研究に比較してワーカーの実証作業を 19～60 倍改善している。結果として得られる証明は計算に関係なく 288 バイトという非常に小さなもの (RSA-2048 署名よりわずかに大きい) である。計算をゼロ知識にすることも安価であり、無視できる程度のオーバーヘッド (鍵生成に 213μs、証明生成に 0.1%) の追加だけで済む。

これらの改善は有望だが、オーバーヘッドが実際の実用性に影響する前にさらなる進歩が必要になる可能性がある。ただし、現在でも高い保証を必要とするシナリオや、Pinocchio がサポートするゼロ知識の特性を必要とするシナリオではこのオーバーヘッドが許容されるケースがある。

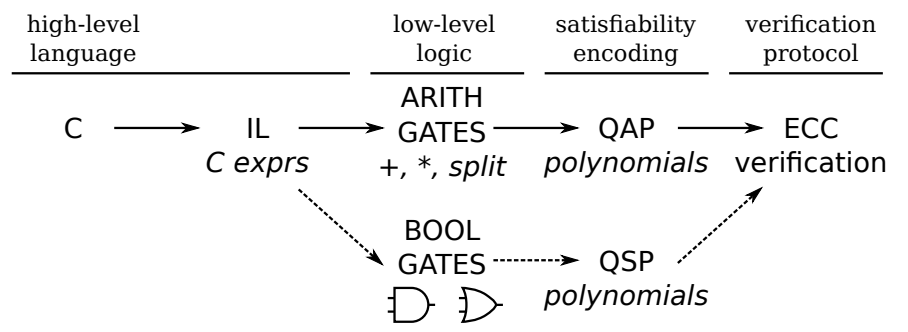
効率的に検証可能な計算を実現するために、Pinocchio は計算を検証するための end-to-end ツールチェーンを生成するための、Gennaro ら [30] によって導入された計算モデルである二次プログラム (quadratic program) と一連の論理的改良およびシステムエンジニアリングを組み合わせる。具体的には、改良されたプロトコルと証明技術により鍵生成のコストを 61% 削減し、証明の生成コストを 64% 削減した。開発者の観点では、Pinocchio は C コードを回路表現に変換し (我々はブール演算と算術演算の両方をサポートする)、その回路を二次プログラムに変換してから暗号プロトコルを実行するプログラムを生成するコンパイラを提供する (Fig.1)。

Figure 1: Ponocchio ツールチェーンの概要. Pinocchio は高レベルの C プログラムを、検証済みの方法でプログラムを実行する実行可能形式の分散セットまで持って行く。二次算術プログラム (§2.2.1) による算術回路と二次スパンプログラム (§2.2.2) によるブール回路の両方をサポートする。

Pinocchio の end-to-end ツールチェーンとブール回路、算術回路の両方のサポートにより、検証の恩恵を受ける実際のアプリケーションを実装することができる。特に、行列乗算の 2 形式、多変量多項式評価、画像照合、全対最短経路、格子気体科学シミュレータ、および SHA-1 を実装する。最初の 3 つのアプリケーションは効率的に演算回路に変換されることが分かり (§5)、従って Pinocchio は同じプログラムをネイティブで実行するよりも早くその結果を検証することができる。後者の 4 つのアプリケーションは不等式の評価やビット単位の演算に依存しているため変換の効率が低下しているが、それでもゼロ知識アプリケーションに役立つ可能性がある。

Contributions. 要約するとこの論文は次のようにコントリビュートしている:

  1. 1 つまたは複数の信頼できないワーカーによって実行される計算を効率的に検証するための end-to-end システム。これには C コードを検証に適したフォーマットに変換するコンパイラと、実際のプロトコルを実行するためのツール一式が含まれる。
  2. 処理時間を 5～7 桁低下させ妥当な領域に入る、理論およびシステムレベルでの改善。
  3. 7 つの実際の C アプリケーションの評価。一部のアプリケーションでは 32 ビットネイティブ整数実行よりも高速な検証を示す。

2 背景

2.1 検証可能計算 (VC)

公開の検証可能計算 (VC) スキームは、計算能力の制限されたクライアントが入力 \(u\) の関数 \(F\) の評価をワーカーにアウトソーシングすることを可能にする。そしてクライアントは、関数評価に必要な作業よりも少ない作業を実行して、返された結果 \(F(u)\) の正確性を検証することができる。

より正しくは公開 VC を以下のように定義し、過去の定義 [22, 29, 30] を一般化する。

定義 1 (Public Verifiable Computation)

公開検証可能計算スキーム \(\mathscr{VC}\) は以下のように定義される 3 つの多項式時間アルゴリズム (\({\sf KeyGen}\), \({\sf Compute}\), \({\sf Verify}\)) のセットで構成される。

  • \((EK_F,VK_F) \leftarrow {\sf KeyGen}(F, 1^\lambda)\): ランダム化された鍵生成アルゴリズムは関数 \(F\) をアウトソースし、セキュリティパラメータ \(\lambda\) を取る。公開評価鍵 \(EK_F\) と公開検証鍵 \(VK_F\) を出力する。
  • \((y,\pi_y) \leftarrow {\sf Compute}(EK_f,u)\): 決定論的ワーカーアルゴリズムは公開評価鍵 \(EK_F\) と入力 \(u\) を使用する。\(y \leftarrow F(u)\) と \(y\) の正しさの証明 \(\pi_y\) を出力する。
  • \(\{0,1\} \leftarrow {\sf Verify}(VK_F,u,u,\pi_y)\): 検証鍵 \(VK_F\) が与えられると、決定論的検証アルゴリズムは \(F(u)=y\) の場合に 1 を出力し、そうでなければ 0 を出力する。

過去の研究では正確性、セキュリティ、および効率 [30] の正式な定義を与えているため、ここではそれらを単純にまとめている:

  • 正確性. 任意の関数 \(F\) と \(F\) への任意の入力 \(u\) に対して、\((EK_F,VK_F) \leftarrow {\sf KeyGen}(F,1^\lambda)\) と \((y,\pi_y) \leftarrow {\sf Compute}(EK_F,u)\) を実行すると、常に \(1 = {\sf Verify}(VK_F,u,y,\pi_y)\) が得られる。
  • セキュリティ. 任意の関数 \(F\) と任意の多項式時間敵対者 \(\mathscr{A}\) に対して \({\rm Pr}[(\hat{u},\hat{y},\hat{\pi}_y) \leftarrow \mathscr{A}(EK_F,VK_F): F(\hat{u}) \neq \hat{y} \ \ \mbox{and}\ \ 1 = {\sf Verify}(VK_F,\hat{u},\hat{y},\hat{\pi}_y)] \le {\rm negl}(\lambda)\) である。
  • 効率. KeyGen は多くの計算でコストが償却される 1 回限りの操作であると想定しているが、Verify は \(F\) を評価するよりも低コストである必要がある。

過去のいくつかの VC スキーム [22, 23] は公開ではなく検証者が指定されているものであった。つまり検証鍵 \(VK_F\) は秘密にしておく必要があった。実際、これらのスキームでは検証関数の出力 (つまりワーカーが不正行為を行ったかどうか) を明らかにするだけでシステムへの攻撃につながる可能性がある。公開 VC スキームはこのような問題を回避する。ゼロ知識検証可能計算 (Zero-Knowledge Verifiable Computation). また我々はアウトソースされた計算がクライアントの入力 \(u\) とワーカーからの補助入力 \(w\) の 2 つの入力を取る関数 \(F(u,w)\) である拡張された設定も考慮している。クライアントが計算の出力以外にワーカーの入力について何も知識を持たない場合、VC スキームはゼロ知識である1。

ゼロ知識はワーカーの入力がプライベートである実用的なシナリオに関連している。例えば匿名で承認するために、ワーカーの入力 \(w\) は第三者からの署名である可能性がある。クライアントの入力 \(u\) はサードパーティの公開鍵であり、関数 \(F(u,w)\) は署名を検証する。クライアントはワーカーが有効何印象譲歩を保持していることを学習するが、認証情報自体については何も学習しない。別の潜在的なアプリケーションでは、例えばスマートメータ請求 [32] のコンテキストで機密データをプライベートに集計するためのものであり、個々のメーターの読み取りはクライアントには非公開である必要があるが、ユーティリティは支払いの総額を認証する必要がある。

Figure 2: 算術回路と等価 QAP. 各ワイヤー値は体 \(\mathbb{F}\) に由来し全ての操作は \(\mathbb{F}\) 上で実行される。QAP の多項式は 2 つの根 \(r_5\) と \(r_6\) での評価によって定義される。詳細は本文を参照。
  • 1 このようなスキームは非対話型ゼロ知識 (NIZK; non-interactive zero-knowledge) 証明 [31] とも呼ばれる

2.2 二次プログラム

Gennaro, Gentry, Parno and Raykova (GGPR) は効率的な VC とゼロ知識 VC スキームを取得するために、計算を二次プログラム (quadratic program) としてコンパクトにエンコードする方法 [30] を最近になって示した。具体的には、算術回路を同等のサイズの二次算術プログラム (Quadratic Arithmetic Program) (QAP) に変換し、ブール回路を同等のサイズの二次スパンプログラム (Quadratic Span Program) (QSP) に変換する方法をである。我々はこれらの変換を要約する。

多項式サイズの回路は多項式時間で動作するチューリングマシンと同等 (多くても対数係数まで) であることを標準的な結果が示している [33]。もちろん、ネイティブハードウェアに対する回路経由の計算の実際の効率はアプリケーションに大きく依存する (例えば、行列計算のための演算回路は本質的なオーバーヘッドを追加しないが、整数乗算のブール回路は単一の 32 ビットアセンブリ命令を実行するより効率が悪い)。

2.2.1 算術回路と QAPs

算術回路は体 \(\mathbb{F}\) から値を運び加算ゲートと乗算ゲートに接続するワイヤーで構成される - Figure 2 参照。我々はそのような回路のエンコーディングである以下の QAP を定義する。

定義 2 (Quadratic Arithmetic Program (QAP [30])

体 \(\mathbb{F}\) 上の QAP \(Q\) には \(m+1\) \(k \in \{0,\ldots,m\}\) に対して多項式の 3 集合 \(\mathscr{V}=\{v_k(x)\}\), \(\mathscr{W}=\{w_k(x)\}\), \(\mathscr{y}=\{y_k(x)\}\) とターゲット多項式 \(t(x)\) が含まれている。\(F\) を、\(\mathbb{F}\) 上の \(n\) 個の元を入力に取り \(n'\) 個の元を出力する関数とする。これは合計して \(N=n+n'\) 個の I/O 元を持つ。そして \((c_1,\ldots,c_N) \in \mathbb{F}^N\) が \(F\) の入出力の有効な割り当てである場合、\(t(x)\) が \(p(x)\) を割り切るような係数 \((c_{N+1},\ldots,C_m)\) が存在するならば、\(Q\) は \(F\) を計算すると言う。ここで:

\[ \eqalignno{ p(x) = & \left(v_{0}(x)+\sum_{k=1}^{m}c_{k}\cdot v_{k}(x)\right)\cdot\left(w_{0}(x)+\sum_{k=1}^{m}c_{k}\cdot w_{k}(x)\right)\cr & -\left(y_{0}(x)+\sum_{k=1}^{m}c_{k}\cdot y_{k}(x)\right)\cdot} \]

言い換えると、\(h(x) \cdot t(x) = p(x)\) となるような多項式 \(h(x)\) が存在しなければならない。\(Q\) のサイズは \(m\)、次数は \(t(x)\) である。

算術回路 \(C\) に対する QAP \(Q\) を作成するのはかなり簡単である。\(C\) の各乗算ゲート \(g\) に対して任意の根 \(r_g \in \mathbb{F}\) を選択し、\(t(x)=\prod_g(x-r_g)\) となるターゲット多項式を定義する。インデックス \(k \in [m] = \{1,\ldots,m\}\) を回路の各入力と乗算ゲートからの出力に割り当てる (加算ゲートは乗算ゲートの根トリビュートに圧縮される)。最後に、\(\mathscr{V}\) の多項式で←入力を各ゲートにエンコードし、\(mathscr{W}\) で右入力を格ゲーと二エンコードし、\(mathscr{Y\) で出力をエンコードすることで \(\mathscr{V}\), \(\mathscr{W}\) および \(\mathscr{Y}\) の多項式を定義する。例えば \(k\) 番目のワイヤーがゲート \(g\) の出力である場合 \(y_k(r_g)=1\) であり、それ以外の場合は \(y_k(r_g)=0\) である。従って、特定のゲート \(g\) とその根 \(r_g\) を考慮すると、式 1 は次のように簡略化される: \[ \begin{eqnarray*} \left( \sum_{k=1}^m c_k \cdot v_k(r_g) \right) \cdot \left( \sum_{k=1}^m c_k \cdot w_k(r_g) \right) & = & \left( \sum_{k \in I_{\rm left}} c_k \right) \cdot \left( \sum_{k \in I_{\rm right}} c_k \right) \\ & = & c_g y_k(r_g) = c_g \end{eqnarray*} \] これはゲートの出力値が入力の積に等しいことを示しており、乗算ゲートの定義そのものである。

要するに、\(t(x)\) が \(p(x)\) を割り切る分割可能性チェックは、それぞれのゲート \(g\) と \(t(x)\) の根 \(r_g\) ごとに 1 つの \(\deg(t(x))\) に分割され、\(p(r_g) = 0\) である。

Figure 2 の回路を具体例として次のように同等の QAP を構築する。まず 2 つの乗算ゲートを表す 2 つの根 \(r_5,r_6 \in \mathbb{F}\) を選択する。つまり QAP の次数は 2 である。各集合 \(\mathscr{V}\), \(\mathscr{W}\) および \(\mathscr{Y}\) に対して 6 つ、入力ワイヤーに対して 4 つ、乗算ゲートからの出力に対して 2 つの多項式を定義する。従って QAP のサイズは 6 である。これらの多項式を乗算ゲートへの各ワイヤの影響に基づいて定義する。具体的には、第三の入力ワイヤーが \(c_5\) の乗算ゲートの左入力に影響するため、\(v_3(r_5)=1\) を除く全てで\(v_k(r_6)=0\) である。同様に、最初の二つの入力はいずれも \(c_6\) ゲートの左入力に影響するため、\(v_1(r_6)=v_2(r_6)=1\) を除き \(v_k(r_6)=0\) である。\(\mathscr{W}\) に対しては正しい入力を調べる。最後に、\(\mathscr{Y}\) は出力を表す。入力ワイヤーはいずれも出力ではないため \(k \in \{1,\ldots,4\}\) に対して \(y_k(r_5)=y_k(r_6)\) であり \(y_5(r_5)=y_6(r_6)=1\) である。

この例の多項式の (多項式の評価に関して) 極端なスパース性に注意。VC プロトコル (§2.3) はこのスパースさを利用して効率を達成する。

実際の構造 [30] は定数による加算と乗算を処理するためもう少し複雑である。それでもなお、GGPR は \(d\) 個の乗算ゲートと \(N\) 個の I/O 要素を持つ任意の演算回路に対して、次数 (根 \(r_g\) の数) \(d\) とサイズ (各集合の多項式数) \(d+N\) で同等の QAP を構築できることを示している。加算ゲートと定数による乗算ゲートは QAP のサイズや次数に影響しないことに注意。従って QAP ベースの VC スキームではこれらのゲートは本質的に "フリー" である。

強力な QAP (strong QAP). 以下に説明する QAP ベースの VC スキームでは、残念ながら GGPR は QAP の強力なプロパティを必要とする。定義 2 では同じ係数の集合 \(c_i\) が 3 つの多項式の集合全てに適用される場合のみを考慮していることに注意。さらに GGPR は定義 2 の if-and-only-if 条件が異なる係数 \(a_i\), \(b_i\), \(c_i\) に適用された場合、すなはち、\[ p(x) = \left( \sum_{k=1}^m c_k \cdot v_k(x) \right) \cdot \left( \sum_{k=1}^m b_k \cdot w_k(x) \right) - \left( \sum_{k=1}^m a_k \cdot y_k(x) \right) \] の場合でも成立することを要求している。それらは QAP をこのより強い条件を満たす強力な QAP に変換する方法を示している。残念ながら、この強化手順により QAP の次数を \(3d+2N\) に増加させ 3 倍以上となる。これにより鍵生成コスト、評価鍵のサイズ、および証明を作成ワーカーの作業量が 3 倍以上となる。

2.2.2 論理回路と QSPs

論理回路は AND, OR, XOR などのビット単位のゲートを使用してビット上で動作する。GGPR は論理回路 [30] のカスタムエンコーディングとして二次スパンプログラム (QSPs; quadratic span programs) を提案する。QSP は表面的には QAP と似ているが、boolean ワイヤー値のみをサポートしているため 2 セットの多項式 \(\mathscr{V}\) と \(\mathscr{W}\) のみを使用する。分割可能性 (divisibility) チェックは \[ p(x) = \left( v_0(x) + \sum_{k=1}^m c_k \cdot v_k(x) \right) \cdot \left( w_0(x) + \sum_{k=1}^m c_k \cdot w_k(x) \right) \] を考慮するように置き換えられる。前述の算術回路ベースの多項式構造に代わり QSP は各 boolean ゲートごとに小さな多項式セットを構築する。具体的には、格ゲーとは 9 個の根と 12 個の多項式を追加する。QAP と同様に QSP には強化ステップが必要である。

2.3 二次プログラムからの VC の構築

二次プログラム (quadratic program) から VC プロトコルを構築するための主なアイディアは、それぞれの多項式、例えば二次プログラム \(v_k(x) \in \mathbb{F}\) が双線形群の元 \(g^{v_k(s)}\) にマップされることである。ここで \(s\) はクライアントが選択した秘匿値、\(g\) は群の生成元、\(\mathbb{F}\) は \(g\) の離散対数の体である。これらの群要素はワーカーに与えられる。ワーカーは所定の入力に対して回路を直接評価し、出力と内部回路ワイヤーの値を取得する。これらの値は二次プログラムの係数 \(c_i\) に対応する。従って VC ワーカーは \(g^{v(s)\) を得るために "指数内で" (in the exponent) \(v(s)=\sum_{k \in [m]} c_k \cdot v_k(s)\) を評価することができる。\(w(s)\) と \(y(s)\) も同様に指数で行える。最後にワーカーは \(h(x)=p(x)/t(x)=\sum_{i=0}^d h_i \cdot x^i\) を計算し、評価鍵の \(g^{s^i}\) 項とともに \(h_i\) を使用して \(g^{h(s)}\) を計算する。大幅に単純化すると証明は \((g^{v(s)},g^{w(s)},g^{y(s)},g^{h(s)})\) で構成される。検証者は双線形写像を使用して \(p(s)=h(s)t(s)\) をチェックする。実際のプロトコル (プロトコル 1) は、ワーカーがクライアントの入力 \(u\) を正しく組み込み、ワーカーが実際に (例えば) \(v_k(s)\) 値の線形関数として指数部 \(v(s)\) を生成することを保証するために追加の機構が必要であるためもう少し複雑である。

プロトコル 1 (Verifiable Computation from strong QAPs)

  • \((EK_F,VK_F) \leftarrow {\sf KeyGen}(F,1^\lambda)\): \(F\) を \(\mathbb{F}\) から \(N\) 個の入出力値を持つ関数とする。\(F\) を算術回路 \(C\) に変換する; そしてサイズ \(m\) と次数 \(d\) に相当する SQP \(Q=(t(x), \mathscr{V},\mathscr{W},\mathscr{Y})\) を構築する。\(I_{\it mid} = \{N+1,\ldots,m\}\)、つまり IO に関連しないインデックスとする。\(e\) を非自明な双線形写像 (non-trivial bilinear map) [30] \(e: G \times G \to G_T\) とし、\(g\) を \(G\) の生成元とする。

    \(s, \alpha, \beta_v, \beta_w, \beta_y, \gamma \overset{R}{\leftarrow} \mathbb{F}\) を選択する。

    パブリックな評価鍵 \(EK_F\) を以下のように構築する。\[ \matrix{(\{g^{v_{k}(s)}\}_{k\in I_{mid}},\hfill & \{g^{w_{k}(s)}\}_{k\in[m]},\hfill & \{g^{y_{k}(s)}\}_{k\in[m]},\hfill\cr \{g^{\alpha v_{k}(s)}\}_{k\in I_{mid}},\hfill& \{g^{\alpha w_{k}(s)}\}_{k\in[m]},\hfill& \{g^{\alpha y_{k}(s)}\}_{k\in[m]},\hfill\cr \{g^{\beta_{v}v_{k}(s)}\}_{k\in I_{mid}},\hfill& \{g^{\beta_{w}w_{k}(s)}\}_{k\in[m]},& \{g^{\beta_{y}y_{k}(s)}\}_{k\in[m]}\hfill\cr \{g^{s^{i}}\}_{i\in[d]},\hfill& \{g^{\alpha s^{i}}\}_{i\in[d]}\hfill & \hfill&)} \]

    パブリックな検証鍵を: \[ VK_F = \left( g^1, g^\alpha, g^\gamma, g^{\beta_v \gamma}, g^{\beta_w \gamma}, g^{\beta_y \gamma}, g^{t(s)}, \{ g^{v_k(s)} \}_{k \in [N]}, g^{v_0(s)}, g^{w_0(s)}, g^{y_0(s)} \right) \] とする。

  • \((y,\pi_y) \leftarrow {\sf Compute}(EK_F,u)\): \(u\) を入力とする。ワーカーは \(F\) に対する回路を評価して \(y \leftarrow F(u)\) を取得する。評価の結果として回路のワイヤー値 \(\{c_i\}_{i \in [m]}\) を知る。

    \(h(x)\) (\(p(x)=h(x) \cdot t(x)\) のような多項式) を時、証明 \(\pi_y\) を以下のように計算する: \[ \eqalignno{(\quad &g^{v_{mid}(s)},\quad g^{w(s)},\quad g^{y(s)},\quad g^{h(s)},\cr &g^{\alpha v_{mid}(s)},\ \, g^{\alpha w(s)},\ \, g^{\alpha y(s)},\ \ g^{\alpha h(s)},\cr &g^{\beta_{v}v(s)+\beta_{w}w(s)+\beta_{y}y(s)}\qquad\qquad\qquad)} \] ここで \(v_{\rm mid}(x) = \sum_{k \in I_{\rm mid}} c_k \cdot v_k(x)\)、\(v(x)=\sum_{k \in [m]} c_k \cdot v_k(x)\)、\(w(x)=\sum_{k \in [m]} c_k \cdot w_k(x)\)、そして \(y(x) = \sum_{k \in [m]} c_k \cdot y_k(x)\) である。これらは線形方程式であるため評価鍵の材料を使って "in the exponent"、つまり \(g^{v(s)} = g^{v_0(s)} \cdot \prod_{k \in [m]} \left( g^{v_k(s)} \right)^{c_k}\) で計算することができる。

  • \(\{0,1\} \leftarrow {\sf Verify}(VK_F,u,y,\pi_y)\): 証明を検証するために、検証鍵 \(VK_F\) にアクセスできる誰でもペアリング関数 \(e\) を使用して \(\alpha\) および \(\beta\) 証明項が正しいことを (例えば \(e(g^{v_{\rm mid}(s)}, g^\alpha) = e(g^{\alpha v_{\rm mid}(s)}, g)\) をチェックすることで) 確認できる。これは \(\alpha\) 項に 8 ペアリング、\(\beta\) 項に 3 ペアリングが必要である。

    最後に、検証者は \(VK_F, g^{v_{\rm io}(s) = \prod_{k \in [N]} (g^{v_k(s)})^{c_k}}\) の要素を使用して係数 \(c_1, \ldots, c_N \in \mathbb{F}\) として表して計算することにより、I/O、\(u\) および \(y\) を表す項を計算できる。

    最後のチェック (3 つのペアリングを持つ) は分割可能性要件を検証する。つまり \[ e(g^{v_0(s)} \cdot g^{v_{\rm io}} \cdot g^{v(s)}, g^{w_{0(s)}} \cdot g^{w(s)}) / e(g^{y_0(s)} \cdot g^{y(s)}, g) = e(g^{h(s)}, g^{t(s)}) \]

    指定された検証者設定 (検証者は \(s\), \(\alpha\) などを知っている) では、ペアリングはこの最後のチェックにのみ必要であり I/O 項は "in the exponent" ではなく \(\mathbb{F}\) を介して直接計算できる。

効率に関して、GGPR [30] は KeyGen の一回限りのセットアップが元の回路のサイズで線形時間 \(O(|C|)\) で実行されることを示している。ワーカーは \(O(|C|)\) で暗号化作業を実行するが、\(h(x)\) を計算するには \(O(|C| \log^2 |C|)\) の非暗号化作業も行わなければならない。このパフォーマンスを達成するためにワーカーは評価ベクトル \((v_k(r_1),\ldots,v_k(r_d))\) の全てが非常にスパースである (\(w\) と \(y\) の多項式についても) という事実を利用する。証明自体は一定の大きさであり、QSP に対しては 7 つの群の要素、QAP に対しては 9 群要素だけであるが、検証者の作業は関数の入力と出力のサイズで線形 \(O(N)\) である。

セキュリティの観点から GGPR [30] はこの VC スキームが \(d\)-PKE および \(q\)-PDH の仮定の下で健全であることを示している (Appendix A 参照)。これは過去の研究 [21, 35, 36] における仮定の弱いバージョンである。\(q\)-PDH 仮定は効率的な改ざん [37] には向かない暗号仮定のクラスに属するが、一部のメンバーは実際に誤りであることが証明されている [38]。Gentry と Wichs は最近、このクラスからの仮定が NP 関係の効率的で非対話的な引数に固有である可能性が高いことを示した [39]。

ゼロ知識 (zero knowledge). VC スキームをゼロ知識にすることは非常に簡単で、目的多項式 \(t(x)\) 自体を多項式集合 \(\mathscr{V}\), \(\mathscr{W}\) および \(\mathscr{Y}\) に含めるだけである。これにより作業者は、乱数 \(\delta_v\), \(\delta_w\), \(\delta_y\) に対して、指数部において \(\delta_v t(s)\) を \(v_{\rm mid}(s)\) へ、\(\delta_w t(s)\) を \(w(s)\) へ、そして \(\delta_y t(s)\) を \(y(s)\) へ加算し、それに応じて証明の他の要素を修正することによって、証明を "randomize" することができる。\(p(x)\) の修正値は \(t(x)\) で割り切れるが、ランダム化によりスキームは統計的にゼロ知識となる [30]。

3 理論的改良

このセクションでは Protocol 1 を改善して回gの生成時間、評価鍵のサイズおよびワーカーの計算量を大幅に削減する。新しいプロトコルのコストモデルは別の場所 [40] で提供されており §5.4 で経験的に改善を分析している。

3.1 Our New VC Protocol

4 Implementation

4.1 Compiler Toolchain

4.2 Quadratic Programs and Cryptographic Protocol

4.2.1 Optimizing Operations

4.3 Applications

5 Evaluation

5.1 Microbenchmarks

5.2 Comparison With Previous Work

5.3 End-to-End Application Performance

5.4 Impact of Our Optimizations

5.5 QSPs versus QAPs

7 Conclusion and Future Work

Acknowledgements

The authors gratefully thank: Peter Montgomery, Michael Naehrig, and Patrick Pierola for assisting us with the cryptographic library used by Pinocchio; Chris Hawblitzel for his sage guidance on compiler development; Rosario Gennaro for valuable discussions; and the anonymous reviewers for their helpful comments. Mariana Raykova was supported by NSF Grant No. 1017660.

References

  1. D. P. Anderson, J. Cobb, E. Korpela, M. Lebofsky, and D. Werthimer, “SETI@Home: An experiment in public-resource computing,” Communications of the ACM, vol. 45, no. 11, 2002.
  2. F. Monrose, P. Wyckoff, and A. Rubin, “Distributed execution with remote audit,” in Proc. of ISOC NDSS, 1999.
  3. P. Golle and S. G. Stubblebine, “Secure distributed computing in a commercial environment,” in Proc. of Financial Cryptography, 2002.
  4. W. Du and M. T. Goodrich, “Searching for high-value rare events with uncheatable grid computing,” in ACNS, 2005.
  5. P. Golle and I. Mironov, “Uncheatable distributed computations,” in Proc. of CT-RSA, 2001.
  6. R. Sion, “Query execution assurance for outsourced databases,” in The Very Large Databases Conference (VLDB), 2005.
  7. M. Castro and B. Liskov, “Practical Byzantine fault tolerance and proactive recovery,” ACM Trans. on Comp. Sys., vol. 20, no. 4, 2002.
  8. B. Carbunar and R. Sion, “Uncheatable reputation for distributed computation markets,” in Financial Cryptography, 2006.
  9. R. Sailer, X. Zhang, T. Jaeger, and L. van Doorn, “Design and implementation of a TCG-based integrity measurement architecture,” in Proc. of the USENIX Security, 2004.
  10. L. Chen, R. Landfermann, H. Lohr, M. Rohe, A.-R. Sadeghi, and ¨ C. Stuble, “A protocol for property-based attestation,” in ¨ Proc. of the ACM Workshop on Scalable Trusted Computing (STC), 2006.
  11. B. Parno, J. M. McCune, and A. Perrig, Bootstrapping Trust in Modern Computers. Springer, 2011.
  12. A. Seshadri, M. Luk, E. Shi, A. Perrig, L. VanDoorn, and P. Khosla, “Pioneer: Verifying integrity and guaranteeing execution of code on legacy platforms,” in Proc. of the ACM SOSP, 2005.
  13. R. B. Lee, P. Kwan, J. P. McGregor, J. Dwoskin, and Z. Wang, “Architecture for protecting critical secrets in microprocessors,” in Proc. of the International Symposium on Computer Architecture (ISCA), 2005.
  14. D. Lie, C. A. Thekkath, M. Mitchell, P. Lincoln, D. Boneh, J. C. Mitchell, and M. Horowitz, “Architectural support for copy and tamper resistant software,” in Proc. of the ACM ASPLOS, 2000.
  15. A.-R. Sadeghi, T. Schneider, and M. Winandy, “Token-based cloud computing: secure outsourcing of data and arbitrary computations with lower latency,” in TRUST, 2010.
  16. S. Goldwasser, S. Micali, and C. Rackoff, “The knowledge complexity of interactive proof systems,” SIAM J. Comput., vol. 18, no. 1, 1989.
  17. S. Arora and S. Safra, “Probabilistic checking of proofs: A new characterization of NP,” J. ACM, vol. 45, no. 1, pp. 70–122, 1998.
  18. J. Kilian, “A note on efficient zero-knowledge proofs and arguments (extended abstract),” in STOC, 1992.
  19. S. Micali, “Computationally sound proofs,” SIAM J. Comput., vol. 30, no. 4, pp. 1253–1298, 2000. Extended abstract in FOCS ’94.
  20. S. Goldwasser, Y. T. Kalai, and G. N. Rothblum, “Delegating computation: Interactive proofs for muggles,” in STOC, 2008.
  21. J. Groth, “Short pairing-based non-interactive zero-knowledge arguments,” in ASIACRYPT, 2010.
  22. R. Gennaro, C. Gentry, and B. Parno, “Non-interactive verifiable computing: Outsourcing computation to untrusted workers,” 2010.
  23. K.-M. Chung, Y. T. Kalai, and S. P. Vadhan, “Improved delegation of computation using fully homomorphic encryption,” in CRYPTO, 2010.
  24. C. Gentry, A fully homomorphic encryption scheme. PhD thesis, Stanford University, 2009. crypto.stanford.edu/craig.
  25. J. Thaler, M. Roberts, M. Mitzenmacher, and H. Pfister, “Verifiable computation with massively parallel interactive proofs,” in USENIX HotCloud Workshop, 2012.
  26. G. Cormode, M. Mitzenmacher, and J. Thaler, “Practical verified computation with streaming interactive proofs,” in ITCS, 2012.
  27. S. Setty, R. McPherson, A. J. Blumberg, and M. Walfish, “Making argument systems for outsourced computation practical (sometimes),” in Proceedings of the ISOC NDSS, 2012.
  28. S. Setty, V. Vu, N. Panpalia, B. Braun, A. J. Blumberg, and M. Walfish, “Taking proof-based verified computation a few steps closer to practicality,” in Proc. of USENIX Security, 2012.
  29. B. Parno, M. Raykova, and V. Vaikuntanathan, “How to delegate and verify in public: Verifiable computation from attribute-based encryption,” in IACR Theory of Cryptography Conference (TCC), 2012.
  30. R. Gennaro, C. Gentry, B. Parno, and M. Raykova, “Quadratic span programs and succinct NIZKs without PCPs,” in EUROCRYPT, 2013. Originally published as Cryptology ePrint Archive, Report 2012/215.
  31. M. Blum, A. D. Santis, S. Micali, and G. Persiano, “Noninteractive zero-knowledge,” SIAM J. on Computing, vol. 20, no. 6, 1991.
  32. A. Rial and G. Danezis, “Privacy-preserving smart metering,” in Proc. of the ACM WPES, 2011.
  33. N. Pippenger and M. J. Fischer, “Relations among complexity measures,” J. ACM, vol. 26, no. 2, 1979.
  34. D. Boneh and M. Franklin, “Identity-based encryption from the Weil pairing,” Proceedings of IACR CRYPTO, 2001.
  35. D. Boneh, X. Boyen, and E.-J. Goh, “Hierarchical identity based encryption with constant size ciphertext,” in EUROCRYPT, 2005.
  36. D. Boneh, C. Gentry, and B. Waters, “Collusion resistant broadcast encryption with short ciphertexts and private keys,” in CRYPTO, 2005.
  37. M. Naor, “On cryptographic assumptions and challenges,” in Proceedings of IACR CRYPTO, 2003.
  38. M. Bellare and A. Palacio, “The knowledge-of-exponent assumptions and 3-round zero-knowledge protocols,” in CRYPTO, 2004.
  39. C. Gentry and D. Wichs, “Separating succinct non-interactive arguments from all falsifiable assumptions,” in STOC, 2011.
  40. I. Damgard, “Towards practical public key systems secure against cho- ˚ sen ciphertext attacks,” in IACR CRYPTO, 1991.
  41. “Verifiable computation: Pinocchio.” http://research. microsoft.com/verifcomp/, Mar. 2013.
  42. D. A. Wheeler, “SLOCCount.” http://www.dwheeler.com/ sloccount/.
  43. M. Aliasgari, M. Blanton, Y. Zhang, and A. Steele, “Secure computation on floating point numbers,” in Proc. of ISOC NDSS, 2013.
  44. A. Holzer, M. Franz, S. Katzenbeisser, and H. Veith, “Secure two-party computations in ANSI C,” in Proc. of ACM CCS, 2012.
  45. M. Naehrig, R. Niederhagen, and P. Schwabe, “New software speed records for cryptographic pairings,” in Proc. of LATINCRYPT, 2010.
  46. P. S. L. M. Barreto and M. Naehrig, “Pairing-friendly elliptic curves of prime order,” in Selected Areas in Cryptography (SAC), 2006.
  47. N. Pippenger, “On the evaluation of powers and related problems (preliminary version),” in Proc. of FOCS, 1976.
  48. A. Aho, J. Hopcroft, and J. Ulman, The Design and Analysis of Computer Algorithms. Addison-Wesley, 1974.
  49. G. Adomavicius and A. Tuzhilin, “Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions,” Trans. Knowledge and Data Engineering, vol. 17, no. 6, 2005.
  50. D. A. Wolf-Gladrow, Lattice-Gas Cellular Automata and Lattice Boltzmann Models: An Introduction. Springer, 2005.
  51. R. Motwani and P. Raghavan, Randomized Algorithms. Cambridge University Press, 1995.
  52. Y. Ishai, E. Kushilevitz, and R. Ostrovsky, “Efficient arguments without short PCPs,” in IEEE Conference on Computational Complexity, 2007.
  53. C. Gentry, S. Halevi, and N. Smart, “Homomorphic evaluation of the AES circuit,” in Proceedings of CRYPTO, 2012.
  54. Y. Chen and R. Sion, “To cloud or not to cloud? Musings on costs and viability,” in Proc. of the ACM Symposium on Cloud Computing, 2011.
  55. G. O. Karame, M. Strasser, and S. Capkun, “Secure remote execution of sequential computations,” in Intl. Conf. on Information and Communications Security, 2009.
  56. S. Arora, C. Lund, R. Motwani, M. Sudan, and M. Szegedy, “Proof verification and the hardness of approximation problems,” J. ACM, vol. 45, no. 3, 1998.
  57. D. Malkhi, N. Nisan, B. Pinkas, and Y. Sella, “Fairplay—a secure twoparty computation system,” in Proc. of USENIX Security, 2004.
  58. Y. Huang, D. Evans, J. Katz, and L. Malka, “Faster secure two-party computation using garbled circuits,” in USENIX Security, 2011.
  59. B. Kreuter, abhi shelat, and C.-H. Shen, “Billion-gate secure computation with malicious adversaries,” in Proc. of USENIX Security, 2012.
  60. S. Setty, B. Braun, V. Vu, A. J. Blumberg, B. Parno, and M. Walfish, “Resolving the conflict between generality and plausibility in verified computation,” in Proc. of the ACM European Conference on Computer Systems (EuroSys), Apr. 2013.
  61. V. Vu, S. Setty, A. J. Blumberg, and M. Walfish, “A hybrid architecture for interactive verifiable computation,” in IEEE Symposium on Security and Privacy, May 2013.
  62. J. B. Almeida, E. Bangerter, M. Barbosa, S. Krenn, A.-R. Sadeghi, and T. Schneider, “A certifying compiler for zero-knowledge proofs of knowledge based on σ-protocols,” in Proc. of ESORICS, 2010.
  63. S. Meiklejohn, C. C. Erway, A. Kupc¸ ¨ u, T. Hinkle, and A. Lysyanskaya, ¨ “ZKPDL: A language-based system for efficient zero-knowledge proofs and electronic cash,” in Proc. of USENIX, 2010.
  64. M. Backes, M. Maffe, and K. Pecina, “Automated synthesis of privacypreserving distributed applications,” in Proc. of ISOC NDSS, 2012.
  65. R. Cramer, I. Damgard, and B. Schoenmakers, “Proofs of partial ˚ knowledge and simplified design of witness hiding protocols,” in Proc. of CRYPTO, 1994.
  66. J. Groth and A. Sahai, “Efficient non-interactive proof systems for bilinear groups,” in Proc. of EUROCRYPT, 2008.
  67. D. Boneh and X. Boyen, “Short signatures without random oracles,” in EUROCRYPT, 2004.
  68. R. Gennaro, “Multi-trapdoor commitments and their applications to proofs of knowledge secure under concurrent man-in-the-middle attacks,” in CRYPTO, 2004.

A Cryptographic Assumptions

B Security Proof for Our VC Scheme

翻訳抄

  1. Bryan Parno, Jone Howell, Graig Gentry, Mariana Raykova, Pinocchio: Nearly Practical Verifiable Computation (HTML), 2013 IEEE Symposium on Security and Privacy, (2013)
  2. Karim Baghery (2016) A short report on: Pinocchio: Nearly Practical Verifiable Computation