ナッシュ均衡

2024年2月16日

概要

ナッシュ均衡 (Nash equilibrium) は各プレーヤーの戦略が互いに最適反応となっている状態である。つまり、集団の中で 1 人が戦略を変えたとしても本人の利得が増えない状況がすべてのプレーヤーに対して成り立っている状態である。

プレーヤー \(i\) の選択することのできる戦略 (行動) の集合を \(A_i = \{a_{i1},a_{i2},\ldots,a_{iN}\}\) とし、\(i\) が実際に選択した戦略を \(a_i \in A_i\) と表す。またすべてのプレーヤーが選択した戦略の組み合わせを \(a^* = (a_1, a_2, \ldots, a_i, \ldots)\) と表す。

ある戦略の組み合わせ状況でのプレーヤー \(i\) の利得 \(g_i(a^*)\) に対して、\(i\) のみが \(a_i\) から \(a_i' \in A_i\) に戦略を変えたときの利得を \(g_i(a^*_{-i},a_i')\) とすると、ナッシュ均衡はすべてのプレーヤーに対して式 (\(\ref{nash}\)) が成り立つ状況である。\[ \begin{equation} g_i(a^*) \ge g_i(a_{-i}^*, a_i') \label{nash} \end{equation} \] ナッシュ均衡を表す式 (\(\ref{nash}\)) はプレーヤー \(i\) のみが戦略を変えても \(i\) の利得は多くならないという状況を意味している。

ナッシュ均衡は必ずしもパレート効率的 (全体の効率が最大化している状態) ではないことに注意。またナッシュ均衡は複数存在することがあり、ある均衡が他の均衡より全体として効率的であることがある。

概要
例1. 囚人のジレンマ
例2. 技術の選択
例3. ホテリングの立地ゲーム
例4. 道路交通
参考文献

例1. 囚人のジレンマ

問題設定: 二人の囚人 1 と 2 が独房で別々に尋問を受けている。囚人は黙秘するか告白するかのどちらかの行動を取ることができる。ここで囚人の刑量を:

両者が黙秘すればそれぞれ禁固 1 年で済む。
両者が告白すればそれぞれ禁固 3 年となる。
片方のみが告白すれば、告白した方は無罪放免となり、黙秘した方は禁固 5 年となる。

と定めるとき、囚人はどのように意思決定するかを考える。

囚人のジレンマのプレーヤーは \(i \in \{1,2\}\)、戦略は \(A_1=A_2=\{\text{黙秘},\text{告白}\}\) であり、禁錮年数は効用 (利得) と見なすことができる。この利得表は Table 1 のように表すことができる。

Table 1. 囚人のジレンマの利得表。
		囚人 2
		黙秘	告白
囚人 1	黙秘	\((-1, -1)\)	\((-5, 0)\)
囚人 1	告白	\((0, -5)\)	\((-3, -3)\)

囚人 1 にとっては、囚人 2 が黙秘/告白のどちらの行動を取ったとしても自身は告白した方が得であることが分る。これは囚人 2 にとっても同様である。したがって囚人のジレンマは相手の判断に関わらず告白する方が常に得であり、ナッシュ均衡は「互いが告白する」ことである。このように他の参加者がどのように判断しても常に最適な戦略がある場合、その戦略を支配戦略と呼ぶ。

全体にとって効用が最大化する "パレート効率的" な状況は両者が黙秘することだが、この選択はナッシュ均衡になっていないため (例え事前に黙秘で申し合わせていたとしても) 実現が困難である。両者の最大利益ではない戦略をとらざるを得ない状況が囚人のジレンマと呼ばれる理由である。

例2. 技術の選択

問題設定: 2 人のエンジニアが Mac か Windows を買おうとしている。ただし 2 人とも同じ OS でなければ作業ができない。彼らの作業には Windows より Mac の方が向いている。

Table 2. 技術の選択の利得表。
		エンジニア 2
		Mac	Windows
エンジニア 1	Mac	\((3, 3)\)	\((0, 0)\)
エンジニア 1	Windows	\((0, 0)\)	\((2, 2)\)

このときナッシュ均衡は Mac-Mac または Windows-Windows で双方が同じマシンを買うことである。この例のように相手に合わせた方が得をすることをネットワーク外部性があると言う。ネットワーク外部性がある状況では複数の均衡が存在することが多く、特定の均衡が他の均衡より良いという状況がある。

複数のナッシュ均衡があるときにどの均衡が選ばれるかを予想することは難しく、現実にはたまたまシェアの大きくなったものが支配的にデファクトスタンダードとなることが多い。双方が Mac を選択すれば最良だが、現実は最良でない均衡にはまってしまうこともある。この場合、個々の参加者の努力ではその状況から抜け出すことは困難である。

例3. ホテリングの立地ゲーム

問題設定: ある通りにプレーヤー 1 と 2 がそれぞれ店を出そうとしている。客は通りの上に均等に分布しており、自分に近い方の店を利用する。もし 2 つの店が同じ場所にあれば、客は双方の店を均等に利用するものとする。このゲームは、双方のプレーヤーが自分の店により多くの客が入るように店を出す場所を決める。

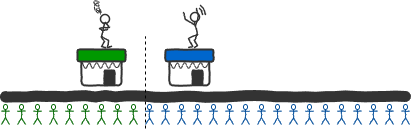
Hotelling's location game — Fig 1. ホテリングの立地ゲーム。通りにいる客は自分が近い方の店を利用する。

この問題は利得表に表すことができないが、以下のように推論することができる。

1 と 2 が異なる場所に店を出す場合、双方ともより相手の店の近くになるように判断を変えた方が自分の客 (利得) が多くなるためナッシュ均衡ではない。
1 と 2 が通りの中央ではない同じ場所に店を出す場合、双方ともより中央に近い位置に判断を変えた方が自分の客が多くなるためナッシュ均衡ではない。
1 と 2 が通りの中央の同じ場所に店を出す場合、双方とも位置を変えると自分の客が少なくなることからナッシュ均衡である。

したがってこのゲームのナッシュ均衡は双方のプレーヤーが通り中央の同じ場所に店を出すことである。

例4. 道路交通

問題設定: A 地点と B 地点をつなぐ 3 つのルートがあり、それぞれの距離を 25km, 20km, 35km とする。ここで 150 台の車が A から B へ移動しようとしているが、同じルートを選択した車が多いと混雑して到着までの所要時間が増加する。車はルート上に他の車が居なければ時速 60km/h で (つまり 1km を 1 分で) 走行できる。単純化のため、本来の所要時間に (そのルートを選択した車の台数÷10) 分を加算したものを実際の所要時間とする。