認知科学

論文翻訳: Graph learning: How humans infer and represent networks

Takami Torao 2019年の論文 #認知科学 #GraphLearning #CognitiveEngineering
  • このエントリーをはてなブックマークに追加

Christopher W. Lynnaa and Danielle S. Bassettabcdef1

This manuscript was compiled on September 17, 2019

Abstract

人は、文中の単語や音楽のメモから講義や本の抽象的な概念まで、一連の項目を使用して情報の伝達、受信、保存を行っている。これらの項目 (ノード) とそれらの間の連続的な遷移 (エッジ) によって形成されるネットワークは人間のコミュニケーションと知識の重要な構造的特徴を符号化している。しかし、どうやって人間は項目のシーケンスの基礎となる確率的遷移のネットワークを学習しているのだろうか? さらに、これらのネットワークの内部マップはどのようになっているのだろうか? ここでは、人間が周囲の世界のネットワークをどのように学習し、表現するかを研究するとに焦点を当てた、成長中の学術的分野であるグラフ学習 (graph learning) を紹介する。まず、人間が連続した項目間の遷移確率の違いを検出する能力があることを示す統計的学習による確立された結果を説明する。次に、遷移確率の違いを直接制御する最近の実験を紹介し、人間の行動も遷移の抽象的なネットワーク構造に大きく依存することを示す。最後に、我々は認知科学者やネットワーク科学者からの創造的な洞察を必要とするグラフ学習の研究における多くのエキサイティングな未解決問題を強調している。

Keywords: graph learning | statistical learning | network science | knowledge networks

Table of Contents

  1. Abstract
  2. 遷移確率を学ぶ
  3. 遷移のネットワーク構造を学ぶ
    1. 局所的構造を学ぶ
    2. 中規模と大域的構造を学ぶ
    3. 遷移確率の違いを制御する
  4. ヒューマングラフ学習のモデリング
  5. グラフ学習の将来
    1. 既存のグラフ学習パラダイム
      1. 定常性
      2. マルコフ特性
      3. 情報探索
    2. 実世界ネットワーク構造の研究
  6. 結論と展望
  7. Acknowledgements
  8. 翻訳抄

日常生活は一連のスナップショットで構成されており、それぞれの瞬間は基礎となる規則と遷移のネットワークに従って次の瞬間に変わる。人間は未来を予測するためにこの遷移のネットワークを推測し、原因と結果のメンタルマップを形成しなければならない。実際、脳の主要な機能の一つは、過去の経験を支配する統計的構造を推測することであり (1, 2, 3, 4)、言語を理解し解釈することを可能にし (5, 6)、刺激 (stimuli) の連続的な流れを解析することを可能にし (5, 7)、社会的直観を構築し (8, 9)、抽象的な推論を実行し (10)、視覚パターンを分類することを可能にしている (11)。8 ヵ月の子供でさえ単語間の境界を識別するために話し言葉の統計的な規則性を検出している (5)。このように、ネットワークの構造を迅速かつ正確に学習する能力は幅広い認知機能をサポートする。

複雑な関係を推論及び表現する我々の能力は、人間がネットワーク化されたシステムの抽象的な並びを構築する原動力にもなっている。今日では、言語 (13, 14) や音楽 (15) からソーシャルネットワーク (16, 17)、インターネット (18)、芸術や科学を構成する概念のウェブ (19, 20) に至るまで、個別のコンポーネント (12) のネットワークを使用して情報を通信、受信、保存を行っている。したがって、人間がどのようにしてネットワークを学習し表現するかを研究することは、我々が多くの基本的な認知機能をどのように実行するかについての理解をもたらすだけではなく、我々の周りの世界における人工ネットワークの構造と機能にも光を当てることになる。

ここでは、人間の認知と行動に対するネットワーク構造の影響を測定および理解するために最近開発された実験技術とネットワークベースのモデル、理論および直感に及ぶグラフ学習の分野について簡単に紹介する。統計的学習と言語学からの実験的方法を利用し、ネットワーク科学、情報理論、強化学習からの計算技術に基づいて構築されているこの分野の高度に学術的な性質を考慮して、簡単な動機付けのある例を用いてアクセス可能な概観を示すことを目的とする。

まず人がどのようにして並びの中の項目間の遷移確率の変動を学習し検出するのか、そしてそのような遷移がどのように連結され全体の並びの大規模構造を符号化するネットワークを形成するのかを示す実験結果について議論する。次に、遷移確率の違いを直接制御することにより、人間の行動に対するネットワーク構造の影響を測定する最近の実験を提示し、これらのネットワーク効果を説明するために提案された計算モデルを説明する。最後に我々は既存のグラフ学習パラダイムの重要な一般化および現代世界における人工ネットワークの理解に対する直接的な意味合いを含む、グラフ学習の最近の進歩に由来するいくつかのオープンな研究の方向性を強調して締めくくる。

遷移確率を学ぶ

人間が環境を移動する際には、予想、計画、知覚のすべてにおいて経験を支配する統計的規則性の正確なマップを必要とする (21, 22, 23)。一連の刺激または事象が与えられたとき、学習者が利用できるもっとも単純な統計は様々な項目の頻度およびそれらの間の遷移 (または条件付き) 確率である。当選のことながら、人間が環境から統計的な規則性を抽出する方法を解明することを目的とする統計学習の分野では主にこれらの単純な統計に焦点が当てられてきた。指針となる例として、単語間の休止や境界線なしに連続した流れの中で異なる音節が遷移する話し言葉を考える (24)。人々はどのようにしてこのような連続したデータの流れをセグメント化し、ある単語がどこから始まり、別の単語がどこから始まるのかを認識するのだろうか。その答えは研究によって確実に確立しているように (25, 26, 27, 28)、音節間の遷移の統計的性質にある。

連続した発話から単語を検出する能力は、それぞれが 3 つの音節からなる 4 つの疑似単語のシーケンス (Fig.1A) を幼児に聞かせた Saffran ら (5) によって最初に実証された。各単語の音節の順序は一貫しており、単語内の遷移確率は 1 であった。ただし単語の順序はランダムで単語間の遷移確率は 1/3 だった。幼児はこの音節の遷移確率の違いを確実に検出することができたことから、言語習得中の単語識別のための説得力のあるメカニズムを提供することができた。この実験のパラダイムは、色 (29) や形 (11) から視覚シーン (30) および物理的動作 (31) に至る刺激を用いて、他の領域における統計的学習を研究するために一般化されてきた。実際、遷移確率の変動を明らかにする能力は、今や人間の学習の中心的かつ一般的な特徴として認識認識されている (25, 26, 27, 28, 32)。

Fig. 1. Saffran ら (5) による加工言語の音節間の遷移。(A) 4 つの異なる疑似単語を含むシーケンス: todaro (青), bikuti (緑), budopa (赤) および pigola (黄)。話すときのシーケンスは単語間の明瞭な区切りなしに音節の連続した流れを形成する。ある音節から別の音節への遷移確率は、単語内で遷移が発生する場合は 1、音節間で遷移が発生する場合は 1/3 である。個の遷移確率の違いにより、乳児は話し言葉を個別単語に分割できる (5, 25, 33)。(B) 音節間の遷移はネットワークを形成し、エッジの重みは音節の遷移確率を表している。遷移ネットワークのランダムウォークは、疑似言語の音節のシーケンスを定義する。4 つの疑似単語は、目で、または標準的なコミュニティ検出アルゴリズム (34) を使用して簡単に識別できる明確なコミュニティ (強調表示された領域) を形成する。(35) で適合された。

遷移のネットワーク構造を学ぶ

個々の遷移確率は一連の刺激についての重要な情報を提供するがストーリー全体を伝えているわけではない (36)。また、遷移は結合して複雑なウェブを形成してシーケンス内の高次の統計構造を特徴づける。これらの統計醸造を研究するために科学者はますますネットワーク科学の言語 (37) に注目を集めており、ネットワーク内のノードとして刺激または項目を概念化し、それらの間の可能な遷移を定義している (Figs 1B and 2)。次に、一連の刺激を、この基礎となる遷移ネットワークをウォークスルーするように表すことができる (38, 38, 39, 40, 41)。この観点は人工文法学習の研究 (42, 43, 44, 45) において特に有用であり、そこでは人間の被験者は人工言語の基礎となる文法規約 (すなはち文字と単語の間の遷移ネットワーク) を推論するタスクを課せられる。

シーケンスの統計的規則性をネットワーク科学の言語に翻訳することによって、様々な遷移構造を特徴づける記述ツールと視覚化手法の強力なセットを継承する。たとえば Saffran ら (5; Fig. 1A) の統計的学習実験をもう一度考えてみよう。遷移構造をネットワークとして可視化するだけで (Fig. 1B) 音節が自然に 4 つの異なる単語に対応する 4 つの異なるクラスタに分割されることが明らかになる。この観察は次のような重要な疑問を提起してい: 単語を解析する (または他の統計学習タスクを実行する) とき、人々は個々の遷移確率の違いについてのみ敏感なのか、それとも基盤となるネットワークの大規模な特徴も明らかにするのか? 以下ではまさにこの問題に焦点を当てるグラフ学習の最近の進歩について述べる。

局所的構造を学ぶ

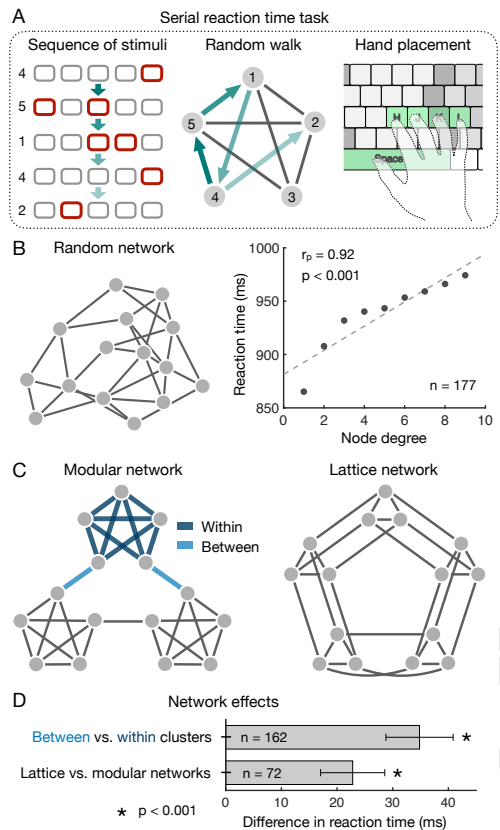
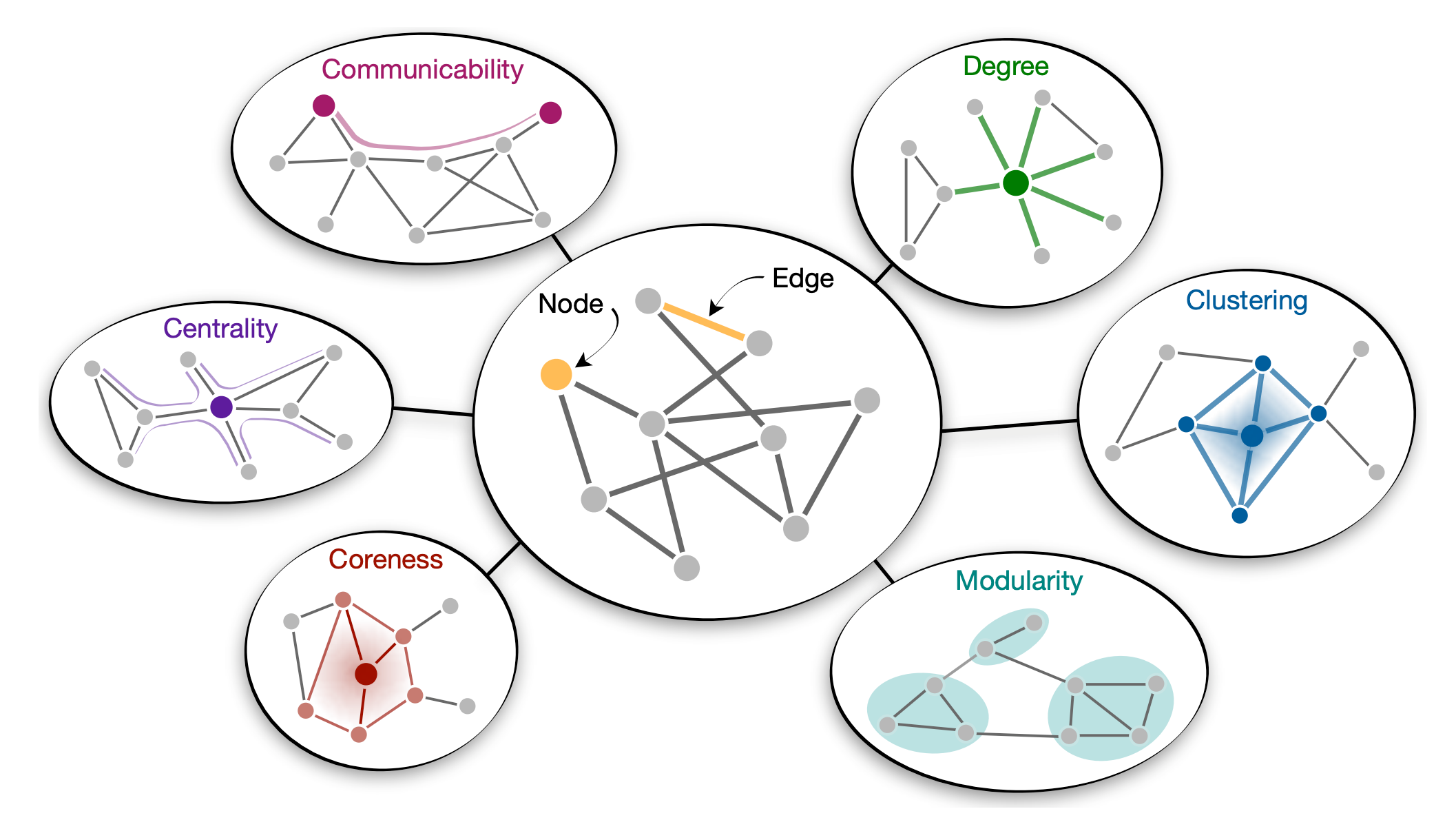
ネットワークのもっとも単純な特徴は個々のノードとエッジに関連漬けられた特徴である (Fig. 2)。例えばノードの次数やその隣接数、エッジの重みはある刺激から別の刺激への遷移確率を決定する。統計的学習の結果に基づいた最近の研究では人々がこれらの局所的ネットワーク特性に敏感であることを実証している。指針となる例としては、ネットワーク構造が人の反応時間に与える影響を測定するために設計された実験的パラダイム (46, 47, 48) を検討する一方で、このアプローチの変種 (4, 9, 33, 35, 40, 41, 49) を用いて同様の結果が達成されたことを留意したい。具体的には、各被験者には一連の刺激が示され、刺激の順序は基礎となる遷移ネットワーク (Fig. 3A) 上のランダムウォークによって定義される。被験者はそれぞれの刺激に対してアクションを実行することにより応答するように指示されている (混乱を避けるためネットワーク内のノードへの刺激の割り当ては被験者間でランダム化されている)。被験者が刺激に反応する速度を測定することで遷移構造に対する期待を推測することができる: すなはち、速い反応は強く推測される遷移を反映し、遅い反応は弱く推測される (または意外な) 遷移を反映する (1, 2, 46, 47, 50)。

統計学的学習の過去の成果 (25, 26, 27, 28) を考えると、特定の遷移に対する被験者の予想がより可能性の高い変化に対して増加する (つまり反応時間が減少する) ことを期待すべきである。この予想を検証するために、重みづけされていない無向ネットワークでのランダムウォークに対して、あるノード \(i\) から隣接ノード \(j\) への遷移確率が \(P_{ij}=1/k_i\) で与えられることに我々は注目した。ここで \(k_i\) はノード \(i\) の次数である。実際、研究者らは人の反応時間が過去の刺激の程度と正に相関することを示しており (Fig. 3B)、そのため人はより可能性の高い遷移を予測することができる (46, 47, 48)。興味深いことに、現在の刺激の程度を考慮すると逆のことがいえる: つまり高度の刺激に対してはより迅速に反応する (47) が、これはおそらく高次数のノードがランダムウォーク中に頻繁にアクセスされるという事実によるものである。これらの結果は人がノードとエッジの局所的性質の変動に敏感であることを示しているが、ネットワーク全体の大規模トポロジーについてはどうだろうか?

Fig. 2. ネットワーク特性入門。(中央) 円で示されたノードは刺激、項目またはシーケンス内の状態を表す。線で示されているエッジはあるノードから別のノードに遷移できる場合にノードのペアを接続している。ノード間のエッジの編成はネットワークのトポロジーまたは構造と呼ばれている。(周辺) ネットワークのトポロジーは局所的組織、中規模組織または大域的組織を特徴づける統計情報を使用して説明することができる。例えば最も単純な局所的統計はノードの次数 (緑; Degree) つまりノードから出ているエッジの数である。中規模構造の 2 つの概念には (i) クラスタリング係数 (青; Clustering) つまり接続された三角形とノードのトリプル比率、および (ii) モジュール性 (ターコイズ; Modularity) を含み、内部的に密な接続と外部的に疎な接続を持つノードのコミュニティが存在する。最後に、大域的測定は (i) コアネス (赤; Coreness) つまり低い程度のノードの除去に耐えるノードの能力、(ii) 長距離接続を促進するためのノードの重要性を定量化する媒介中心性 (betweenness centrality) のような中心性の概念 (紫; Centrality) および (iii) 2 つのノードを接続する様々な長さの経路の数を補足する通信可能性 (マゼンタ; Communicability) を含んでいる。全体として、ネットワーク表現と関連する統計は研究中のシステム構造に対する重要な洞察を提供できる。

中規模と大域的構造を学ぶ

過去 10 年の間、研究者たちはネットワークの中規模 (mesoscale) と大域的トポロジーが人間の学習と行動にどのように影響するかについて理解する著しい進歩を遂げた。単語のクラスタリングは中規模特性 (Fig. 2) に関してその獲得を促進することが示されている (51)。対照的に、クラスタリングの低い単語は長期記憶 (52) で認識しやすく、処理 (53, 54) と生産 (55) に利点があることが研究により実証されている。さらに、ネットワークのモジュール性 (4, 35, 46, 47, 48, 49)、すなはちノードが密に接続されたクラスタを形成する傾向と関連する動作および神経活動における著しい変化を発見した。これについては次のサブセクションで説明する。

研究では中規模の特徴に加えて人間の認知に対する大域的ネットワークトポロジーの影響も調査した (Fig. 2)。例えば上記の反応時間実験 (Fig. 3A) では、人は長距離接続を仲介する際のノードの役割の尺度である低い中心性 (46) を持つノードをよく予測することができた。他の実験では、ノードがネットワークにどれほど深く埋め込まれているかの尺度であるコアネスの低い単語を、幼い子供がより容易に獲得して生成することが示され (56)、ニューラルシグネチャがノード対の接続経路数の尺度であるネットワーク通信可能性を反映することが示された (40)。総合すると、これらの結果は大規模なネットワーク構造と人間の認知の間の堅牢で一般的な関係を示している。しかしながら、因果関係を確立するためには上記の効果が実際にはローカルネットワーク構造の変動に左右されないことをも実装しなければならない。

遷移確率の違いを制御する

局所的構造の影響から大規模なネットワーク構造の影響を分離するために、最近の研究ではネットワークの特定のファミリーに焦点を当てることにより遷移確率の違いを直接制御している (4, 35, 46, 47, 48)。重み付けされていない無向ネットワークのランダムウォークの場合、遷移確率はノードの次数によって決定されることは前述の通り。このためすべての遷移確率が等しい確率となるためには一定の程度で変化するトポロジーを持つグラフに単純に焦点を当てることができる。例えば Fig. 3C に示されたモジュラーグラフと格子グラフを考えてみると、両方のネットワークは一定の次数 4 (つまりすべてのエッジで一定の遷移確率 1/4) であるため、ネットワークの異なる部分の間、または 2 つのネットワーク自体の間の挙動または認識の変動は、ネットワークの大域的トポロジーに起因する必要がある。

このアプローチは Schapiro ら (4) によって開発された。彼らは、人がモジュラーグラフ (Fig. 3C) でクラスタ間の仙仁を検出することができ、これらのクラスタ間遷移がクラスタ内遷移と比較して神経活動の異なるパターンをもたらすことを示した。反応時間実験 (Fig. 3A) に戻ると、被験者はクラスタ間遷移よりもクラスタ内遷移に対してより迅速に反応する (つまりより良く予想できる) ことが示された (46, 47; Fig. 3D)。さらに、格子グラフ (46, 47; Fig. 3D) またはランダムに生成された次数 4 のグラフ (48) に比べて、モジュラーグラフの反応時間は全体的な減少を示している。

これらの結果は、他の最近の調査結果 (35, 49) と組み合わせて、局所的構造の違いを制御した後でも、人が大域的ネットワークトポロジーの変動に敏感であることを明確に示している。従って、人は個々の遷移確率を学習できるだけではなく、日々の経験の根底にある複雑な統計的依存関係を明らかに為ることもできる。しかし、過去の観測から遷移ネットワークの高次の特徴をどのようにして学ぶのだろうか?

Fig. 3. 人の行動はネットワークトポロジーに依存する。(A) 被験者に一連の刺激を提示して行動によって応答するように求める連続反応時間実験を考える。ここで各刺激は 5 つの正方形で構成されており、そのうち一つか二つは赤で強調されている (左)。刺激の順序は基盤となるネットワーク (中) のランダムウォークによって決定される。被験者はそれぞれの刺激に対してハイライトされたマス目 (右) に対するキーボードを押す。(B) 15 ノード、30 エッジの Erdös‐Rényi ランダム遷移ネットワーク (左) を考えると、遷移 \(i \to j\) に対する被験者の平均反応時間は先行ノードの \(k_i\) が増加するに連れて増加する (右)。同様に、被験者の反応時間は遷移確率 \(P_{ij} = 1/k_i\) が減少するにつれて増加する (47, 48)。(C) 遷移確率の変動を制御するために一定次数 \(k=4\) の 2 つのネットワークを考える。それぞれ 5 つのノード (左) の 3 つのコミュニティでこうせいされるモジュラーネットワークと周期的境界条件 (右) を持つ 3×5 グリッドを表す格子ネットワーク。(D) 実験はネットワーク構造の 2 つの一貫した効果を示している。第一に、モジュラーネットワークではクラスタ間の遷移の反応時間がクラスター内の遷移よりも長くなる (35, 45, 47, 48, 49)。第二に、反応時間はモジュラーネットワークよりも格子ネットワークの方が平均して長い (46, 47)。

ヒューマングラフ学習のモデリング

グラフ学習実験は人の刺激や事象の予測、すなはち遷移確率の内部表現が遷移ネットワークの大域的トポロジーに決定的に依存することを立証した。人間がこれらの大域的特徴をどのように検出するかを理解し、人の行動について定量的に予測するには、人間が過去の経験から遷移ネットワークを学習する方法の研鑽モデルが必要である。興味深いことに、人間は体系的に最も正確でおそらく最も単純であろう学習規則から逸脱している。

これらの考えを具体化するために、遷移確率行列 \(P_{ij}\) によって記述される一連の刺激を考える。観測された項目のシーケンスが与えられると \(i\) が \(j\) に遷移した回数 (\(n_{ij}\) で示される) を単純に \(i\) が出現した回数 (これは \(\sum_k n_{ik}\) に等しい) で割ることで、項目 \(i\) から別の項目 \(j\) に遷移する確率を推定することができると考えられている。\[ \begin{equation} \hat{P}_{ij} = \frac{n_{ij}}{\sum_k n_{ik}} \end{equation} \] 実際、これはおそらく実行可能な最も単純な推定であるだけではなく、過去の観測からの遷移確率の最も正確な (または最尤の) 推定値でもある。最尤推定の定義的性質は遷移構造の不偏近似を提供することである。つまり、推定遷移確率 \(\hat{P}_{ij}\) は大域的ネットワークトポロジーに関係なく、真の値 \(P_{ij}\) について均等に分布する (57)。しかし、遷移確率が固定値に保持されている場合であっても人の行動と認知は大域的ネットワーク特性に体系的に依存することが分かった (4, 35, 46, 47, 48)。このように最尤推定は人が遷移確率をどのように学習するかについて単純で原理的なモデルを提供するにもかかわらず、人間が遷移ネットワークの大域的特徴を検出する方法を説明できない (47)。

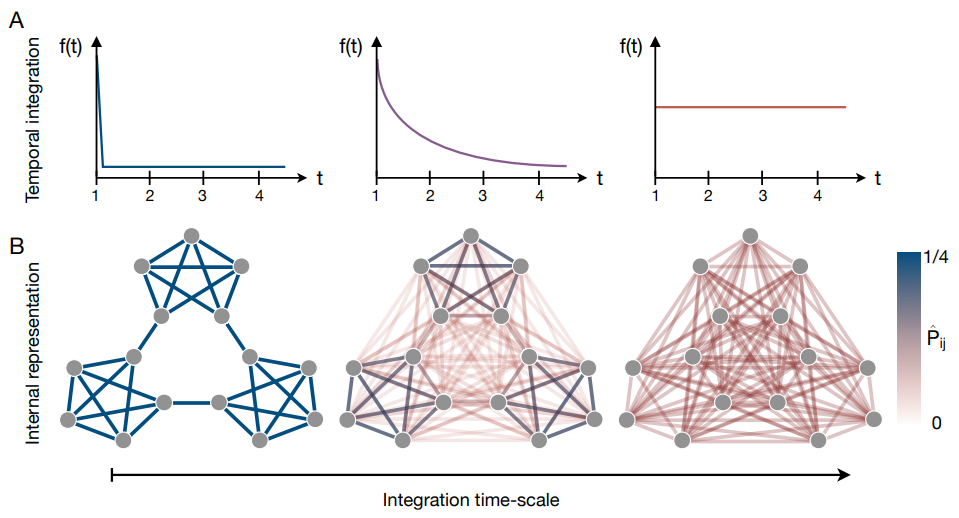
大域的ネットワークトポロジーが人間の認知に及ぼす影響を理解するために、研究者たちは人が遷移ネットワークを学習および表現する方法を説明する多くのモデルを最近になって提案した (4, 40, 47, 48, 58, 59, 60, 61, 62, 63)。特にこれらのモデルの多くは基礎となる共通のメカニズムに依存している。つまり、一連の刺激を観測するとき人は時間の経過と共に遷移構造を統合する (40, 47, 48, 59, 62, 64)。簡単に言えば、(最尤推定と同様に) シーケンス内で直接隣接している項目を接続するだけではなく、二段階、三段階、またはそれ以上離れている項目を関連づけることもある。数学的には、このような時間積分から推定される遷移確率行列の形式は以下のようになる: \[ \begin{equation} \hat{P} = C \sum_{t \ge 1} f(t) P^t \end{equation} \] ここで \(t\) は 2 つの項目間の時間の距離を表し、\(f(g) \ge 0\) は特定の距離の遷移に置かれる重みを定義する減少関数、\(C=(\sum_t f(t))^{-1}\) は正規化定数である。

例えば \(f(t)\) が \(t=1\) を中心とするデルタ関数の場合 (Fig. 4A)、学習者は長さ 1 の遷移に焦点を合わせる。この場合、人は単純に最尤推定を実行し、推定 \(\hat{P}\) は真の遷移構造 \(P\) に収束する (Fig. 4B)。逆に \(f(t)\) がすべての \(t \le 1\) 時間スケールで均一である場合、学習器はすべての距離の遷移を統合し (Fig. 4A)、推定 \(\hat{P}\) は真の遷移構造との類似性を失う (Fig. 4B)。しかし重要なことは中間の時間スケール (Fig. 4A) で遷移を統合する学習者にとっては、密に接続されたノードのコミュニティなどの遷移ネットワークの大域的な特徴がより焦点となり、一方でコミュニティ間のエッジのような局所的特徴のいくつつかが消えてゆくことである (Fig. 4B)。

最近、研究者らは時間統合のプロセスを使用して Fig. 3 に示した反応時間の結果 (47) から強化学習過程の計画 (64)、ランダムシーケンスにおける構造の知覚 (40, 62)、人の情報処理 (48)、および脳における神経活動のパターンの変化 (59, 62) まで、人間の認知に対する観察されたネットワーク効果の多くを説明した。さらに説明のあった効果は反応時間 (46, 47, 48, 65, 66)、データセグメンテーション (4, 35)、タスクエラー (46, 47)、ランダム性検出 (67)、EGG シグナル (68, 69)、および fMRI 記録 (4, 65) を含む、様々なタイプの行動的および神経的観察に及んでいる。加えて、時間的統合のメカニズム自体が生物学的に実行可能であることが示されており (59, 62, 70, 71, 72)、時間的文脈学習から強化学習 (58, 64, 73, 74, 75, 76) まで、既存の認知理論の広い範囲に現れている。統合すると、これらの結果は人間の行動と認知に対するネットワークトポロジーの影響が、個々の遷移確率を学習する能力だけでなく、トポロジースケールを超えて遷移ネットワークの特徴を組み合わせる能力からも現れることを示している。

Fig. 4. 遷移の時間的統合により中規模および大域的ネットワークの特徴が出現する。(A) 時間積分なし(左)、定数積分(右)、および減少積分(中)の積分関数 \(f(x)\) の図。(B) Fig. 3C のモジュラーネットワークの遷移確率の結果の推定 \(\hat{P}\)。時間積分を行わない場合(左)、内部表現は真の遷移ネットワークの最尤推定値である。すべての時間スケールに渡って積分する対象(右)の場合、内部表現は全体となり真の遷移ネットワークとの類似性が失われる。中間の時間的統合ではコミュニティ構造などの遷移ネットワーク高次機能が有機的に注目され(中)、クラスター間の遷移よりもクラスター内の遷移の方が高い予測確率が得られる。(47) より改変。

グラフ学習の将来

グラフ学習に関する過去と現在の進歩は、認知科学、神経科学およびネットワーク科学の交差点で新しい研究課題を喚起する。ここでは実世界の遷移ネットワークの構造と機能を理解するためのグラフ学習の意味を議論する前に、既存の利用可能なグラフ学習パラダイムの一般化から始めていくつかの重要な方向性を強調する。

既存のグラフ学習パラダイム

Fig. 1 と 3 で論議されたものを含む殆どのグラフ学習実験では、被験者には (おそらく重み付き有向) 遷移ネットワークのランダムウォークによって定義される一連の刺激が提示される (4, 5, 9, 33, 35, 38, 39, 40, 42, 43, 44, 45, 46, 47, 48, 49)。同様に、確率過程の言語では各シーケンスは定常マルコフ過程 (77) を表している。ランダムウォークはグラフ学習の研究において自然な出発点を提供するが、それらは 3 つの主要な家庭によっても成約される: (i) 基礎となる遷移構造が時間とともに静的であること(定常性)、(ii) 将来の刺激が現在の刺激のみに依存すること(マルコフ特性)、および (iii) シーケンスが観測者からの入力無しで事前に決定されていること。将来のグラフ学習実験では、既存のグラフ学習パラダイムを体系的に一般することによりこれらの制約の協会をテストすることができる。

定常性

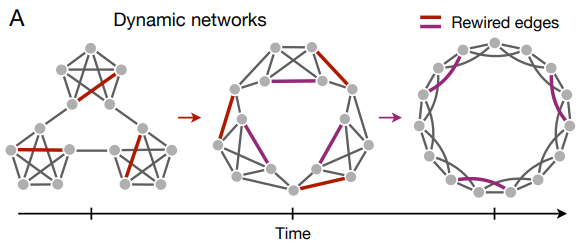
殆どのグラフ学習実験は静的遷移ネットワークに焦点を当てているが、現実世界で遭遇するネットワークの多くは時間とともに変化する (78, 79, 80, 81)。従って単に単一のネットワークを学習する人の能力を調査するのではなく、将来の実験では、動的に進化するネットワーク (Fig. 5A) の一時的な構造的特徴を人間が検出する能力を調査する必要がある。初期の結果によると、ある遷移構造から別の遷移構造へと変換する一連の刺激を観察すると、初期のネットワークで学習された表現が次のネットワークへの反応行動に影響を与えるが、この影響は時間の経過とともに減少してゆく (46)。従って、ネットワーク構造を学習するために必要な観測される遷移の数などのグラフ学習に関する時間スケールが、基礎となるネットワークトポロジー間の遷移の数のようなグラフ進化の時間スケール (81) とどのように関係するかを考えることは興味深い。

マルコフ特性

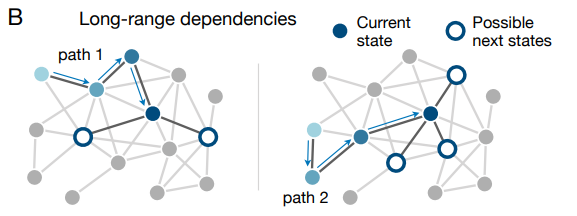
これまでは既存のグラフ学習研究の大部分と同様に、次の刺激が現在の刺激のみに依存するシーケンスのみに使用点を当ててきた。つまり我々はマルコフ特性に (77) に従う並びに焦点を合わせている。しかし現実世界の刺激や項目のほとんどのシーケンスには長期の相関や依存関係を持っている (86; Fig. 5B)。例えば話し言葉における単語の確率は、前の単語だけではなく文の前の単語や文が存在するより広いコンテキストにも依存する (12, 82)。同様に音楽システムではシーケンスの長さと構造に制約を課すことが多く、それによって音譜間の長期依存性を誘導している (83, 84)。興味深いことに人が時間の経過と共に遷移を統合するという証拠が増えている (40, 47, 48, 59, 62, 64) ことを考えると、その結果として得られる遷移構造の内部推定は非マルコフ過程に似ている (47)。従って、将来の研究では刺激の時間的統合により人が日常生活のシーケンスの非マルコフ特性を推測することを可能にするか、この後の研究が可能である。

情報探索

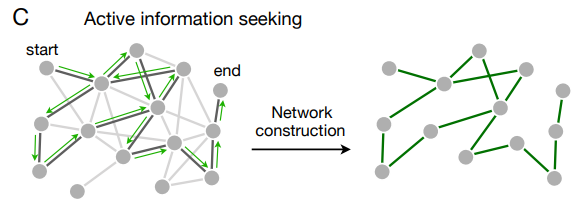
最後に、人間が観測するシーケンスの多くは観察者からの入力なしに規定されているが、シーケンスの構造を決定する際に人が関与する設定も存在する。例えばネットサーフィンをしているとき (85, 90, 91, 92, 93) や、科学論文の引用をたどっているとき (94, 95)、人は基礎となるハイパーリンクと引用ネットワークを通る経路を選択する。このようにして人は単に情報を提示するだけではなくて、遷移構造に関する情報を探し出すことができる (Fig. 5C)。このような情報探索は人によって異なり (85, 92)、基礎となるネットワークのトポロジーに大きく依存することが示されている (85, 90, 91, 93)。グラフ学習のコンテキストでは、被験者が積極的に情報を求めることができるようにすることで多くの魅力的な質問が発生する。遷移ネットワークを経由するパスを選択することで被験者はトポロジーをより効率的に学習できるだろうか? それとも、情報を探す能力があるからこそ、人は真の遷移構造の偏った表現ができるのだろうか (96, 97)? これらの疑問は上記の方向性と組み合わせて、認知科学者とネットワーク科学者からの創造的な洞察と強行の貢献を必要とするエキサイティングなグラフ学習の拡張の一部であることを強調する。

Fig. 5. グラフ学習パラダイムの一般化。
(A) 遷移ネットワークは時間と共に変遷し変化することがしばしばある。このような非定常遷移確率は動的遷移ネットワークを使用して記述することができる。動的遷移ネットワークはエッジを繰り返し再配線することにより、あるネットワーク (左側のモジュラーネットワークなど) から別のネットワーク (右側のモジュラーネットワークなど) に変化する (78, 79, 80, 81)。
(B) 次の状態が現在の状態だけではなく過去の多くの状態にも依存しているように、実世界のシーケンスの多くは長期の依存関係がある (12, 82, 83, 84)。たとえば、表示しているネットワークのパス 1 は次の状態に対して 2 つの可能性をもたらし (左)、パス 2 は 3 つの可能性をもつ状態の異なるセットをもたらす (右)。
(C) 人はしばしば、単に規定されたシーケンスを提示されるのではなく、遷移ネットワークを通るパスを選択することにより積極的に情報を探す。そのような情報探索は歩行者が通過するノードとエッジを含むサブネットワークを生成する (85)。

実世界ネットワーク構造の研究

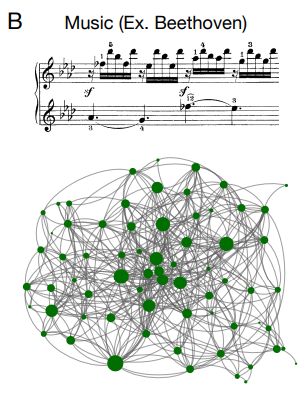
グラフ学習の研究は人間の行動や認知に光を当てるだけではなく現実世界のネットワーク構造や機能にも洞察をもたらす可能性を秘めている。実際、人間の認知とネットワークの間には密接な関係がある。人は、言語 (Fig. 6A) や音楽 (Fig. 6B) を使った通信から、科学やインターネット (Fig. 6C) を使った情報の保存や検索に至るまで幅広いタスクをネットワーク化されたシステムに頼っているが、これらのネットワークの多くは人間と共に進化してきたか、あるいは人間によって明示的に設計されたものである。したがって人がネットワークの構造を学習するのと同じように、一部のネットワークは人間の学習と認知をサポートするように構成されているものがあるのではないかと考える人もいるだろう。

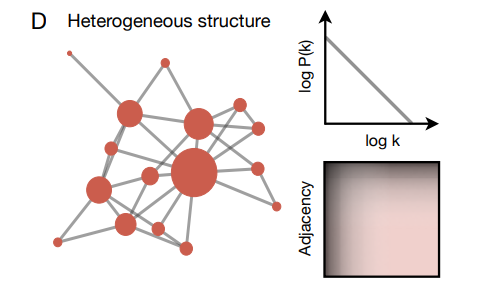
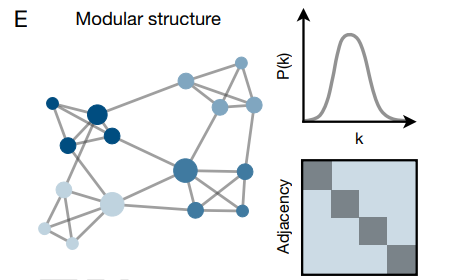
興味深いことに、実世界の多くの遷移ネットワークは二つの異なる構造的特徴を共有している: (i) それらは非常に高い次数のハブノードの存在によって特徴付けられている (19, 88, 98) 異種 (heterogineous) であり (Fig. 6D)、(ii) 密結合クラスター (16, 89, 99, 100) の存在によって特徴付けられているモジュール (Fig. 6E) である。異種性とモジュール性は共に階層的組織化の二つの決定的な特徴を表しており、それらは今や広範な人為的遷移ネットワークで観測されている (87, 101)。これらのネットワークの共通の構造的特徴は、人間の学習とコミュニケーションを促進するという共通の機能的目的の結果として現れているのだろうか?

グラフ学習はこのような疑問に答えるための定量モデルと実験ツールを提供している。例えば Fig. 3 で説明したような実験結果はモジュール構造により遷移を予測する能力が向上することを示しており (46, 47, 48)、この結果は Fig. 4 の形式のモデルを使用して数値的に確認されている (47, 48)。さらに、異種ネットワークに見られる高次のハブは人が情報を検索し (90, 93)、効率的に通信するのに役立つ (48) ことが示されている。まとめると、これらの結果はグラフ学習が我々の周辺世界の遷移ネットワークを研究するためのユニークで建設的なレンズを提供することを示している。

Fig. 6. 実際の遷移ネットワークは階層構造を示す。(D, E) 現実世界の遷移ネットワークの多くは二つのトポロジー機能によって特徴付けられる階層的組織 (87) を示す。
(A) シェークスピアの全作品における単語 (ノード) とそれらの間の遷移 (エッジ) から構築された言語ネットワーク。
(B) ベートーベンのソナタ第23番の音譜間の遷移を表す音楽ネットワーク。
(C) ウィキペディアのページ間のハイパーリンクによって定義される知識ネットワーク。
(D) スケールフリーネットワークに関連づけられることが多い異種構造は、典型的に、べき乗則次数分布と高次ハブノード (88) の存在によって特徴付けられる。
(C) モジュール構造は密なクラスター内接続性と疎なクラスター間接続性 (89) を持つノードのクラスタの存在により定義される。

結論と展望

グラフ学習はこのような疑問に答えるための定量モデルと実験ツールを提供する。例えば Fig. 3 で説明したような実験結果は、世界を統治する統計的規則性を人がどのように学習し表現するかをモジュールで理解することは人間の認知の研究における最大の未解決問題の一つであることを示している。人がどのようにして項目の頻度とそれらの間の遷移確率を検出するかを研究した統計的学習における数十年の研究 (5, 11, 25, 26, 27, 28, 29, 30, 31, 41) に続いて、現在では人の行動や認知、神経活動が遷移の大域的トポロジー (4, 9, 33, 40, 46, 47, 48, 49) に明確に依存することを証明する決定的な証拠が示されている。一連の項目とそれらの間の遷移をネットワークのノードとエッジとしてキャストすることにより、科学者は統一された原理に基づくフレームワーク (37) で人間のの認知に対するネットワーク構造の影響を調べることができる。

この分野の実験的および数値的な基礎は確立されているが、グラフ学習は多くの学際的機械を豊富に提供する研究の新分野のままである。新しい認知モデリング技法 (Fig. 4) および既存の実験パラダイムの拡張 (Fig. 5) から新しい構造の応用まで、人が遷移を予測する能力を向上させ (46, 47, 48)、その結果は Fig. 4 のモデルを用いて数値的に確認された (47, 48)。さらに、異種ネットワークに見られる高度なハブは、人が情報を検索し (90, 93)、効率的に通信するのに役立つことが示されている (48)。まとめると、これらの結果はグラフ学習が我々の周辺世界における遷移ネットワーク (Fig. 6) を研究するためのユニークで建設的なレンズを提供することを示している。グラフ学習は、人間の認知や複雑なネットワーク、それらが交差する無数の方法についての考え方を変えるために準備されている。

Acknowledgements

We thank David Lydon-Staley, Nico Christianson, and Jennifer Stiso for comments on previous versions of the paper. D.S.B. and C.W.L. acknowledge support from the John D. and Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the ISI Foundation, the Paul G. Allen Family Foundation, the Army Research Laboratory (W911NF-10-2-0022), the Army Research Office (Bassett-W911NF-14-1-0679, Grafton-W911NF-16-1-0474, DCIST- W911NF-17-2-0181), the Office of Naval Research, the National Institute of Mental Health (2-R01-DC-009209-11, R01- MH112847, R01-MH107235, R21-M MH-106799), the National Institute of Child Health and Human Development (1R01HD086888- 01), National Institute of Neurological Disorders and Stroke (R01 NS099348), and the National Science Foundation (BCS-1441502, BCS-1430087, NSF PHY-1554488 and BCS-1631550). The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies.

  1. Hyman R (1953) Stimulus information as a determinant of reaction time. J. Exp. Psychol. 45(3):188.
  2. Sternberg S (1969) Memory-scanning: Mental processes revealed by reaction-time experiments. Am. Sci. 57(4):421–457.
  3. Johnson-Laird PN (1980) Mental models in cognitive science. Cogn. Sci. 4(1):71–115.
  4. Schapiro AC, Rogers TT, Cordova NI, Turk-Browne NB, Botvinick MM (2013) Neural representations of events arise from temporal community structure. Nat. Neurosci. 16(4):486–492.
  5. Saffran JR, Aslin RN, Newport EL (1996) Statistical learning by 8-month-old infants. Science 274(5294):1926–1928.
  6. Friederici AD (2005) Neurophysiological markers of early language acquisition: From syllables to sentences. Trends Cogn. Sci. 9(10):481–488.
  7. Reynolds JR, Zacks JM, Braver TS (2007) A computational model of event segmentation from perceptual prediction. Cogn. Sci. 31(4):613–643.
  8. Gopnik A, Wellman HM (2012) Reconstructing constructivism: Causal models, bayesian learning mechanisms, and the theory theory. Psychol. Bull. 138(6):1085.
  9. Tompson SH, Kahn AE, Falk EB, Vettel JM, Bassett DS (2019) Individual differences in learning social and nonsocial network structures. J. Exp. Psychol. Learn. Mem. Cogn. 45(2):253.
  10. Bousfield WA (1953) The occurrence of clustering in the recall of randomly arranged associates. J. Gen. Psychol. 49(2):229–240.
  11. Fiser J, Aslin RN (2002) Statistical learning of higher-order temporal structure from visual shape sequences. J. Exp. Psychol. 28(3):458.
  12. Shannon CE (1948) A mathematical theory of communication. Bell Syst. Tech. J. 27(3):379–423.
  13. Bar-Hillel Y, Carnap R (1953) Semantic information. Br. J. Philos. Sci. 4(14):147–157.
  14. Dretske FI (1981) Knowledge and the Flow of Information.
  15. Cohen JE (1962) Information theory and music. Behav. Sci. 7(2):137–163.
  16. Rosvall M, Bergstrom CT (2008) Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. U.S.A. 105(4):1118–1123.
  17. Gómez-Gardeñes J, Latora V (2008) Entropy rate of diffusion processes on complex networks. Phys. Rev. E 78(6):065102.
  18. Liben-Nowell D, Kleinberg J (2008) Tracing information flow on a global scale using internet chain-letter data. Proc. Natl. Acad. Sci. U.S.A. 105(12):4633–4638.
  19. Newman ME (2001) The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. U.S.A. 98(2):404–409.
  20. Hummon NP, Dereian P (1989) Connectivity in a citation network: The development of dna theory. Soc. Netw. 11(1):39–63.
  21. Koechlin E, Hyafil A (2007) Anterior prefrontal function and the limits of human decisionmaking. Science 318(5850):594–598.
  22. Koechlin E, Corrado G, Pietrini P, Grafman J (2000) Dissociating the role of the medial and lateral anterior prefrontal cortex in human planning. Proc. Natl. Acad. Sci. U.S.A. 97(13):7651–7656.
  23. Wilensky R (1983) Planning and understanding: A computational approach to human reasoning.
  24. Brent MR, Cartwright TA (1996) Distributional regularity and phonotactic constraints are useful for segmentation. Cognition 61(1-2):93–125.
  25. Romberg AR, Saffran JR (2010) Statistical learning and language acquisition. Wiley Interdiscip. Rev. Cogn. Sci. 1(6):906–914.
  26. Aslin RN, Newport EL (2012) Statistical learning: From acquiring specific items to forming general rules. Curr. Dir. Psychol. Sci. 21(3):170–176.
  27. Aslin RN, Newport EL (2014) Distributional language learning: Mechanisms and models of category formation. Lang. Learn. 64(s2):86–105.
  28. Schapiro A, Turk-Browne N (2015) Statistical learning in Brain Mapping: An Encyclopedic Reference. (Elsevier), pp. 501–506.
  29. Turk-Browne NB, Isola PJ, Scholl BJ, Treat TA (2008) Multidimensional visual statistical learning. J. Exp. Psychol. Learn. Mem. Cogn. 34(2):399.
  30. Brady TF, Oliva A (2008) Statistical learning using real-world scenes: Extracting categorical regularities without conscious intent. Psychol. Sci. 19(7):678–685.
  31. Baldwin D, Andersson A, Saffran J, Meyer M (2008) Segmenting dynamic human action via statistical structure. Cognition 106(3):1382–1407.
  32. Himberger K, Finn A, Honey CJ (2019) Reconsidering the automaticity of visual statistical learning.
  33. Karuza EA, Thompson-Schill SL, Bassett DS (2016) Local patterns to global architectures: Influences of network topology on human learning. Trends Cogn. Sci. 20(8):629–640.
  34. Pons P, Latapy M (2005) Computing communities in large networks using random walks in International symposium on computer and information sciences. (Springer), pp. 284–293.
  35. Karuza EA, Kahn AE, Thompson-Schill SL, Bassett DS (2017) Process reveals structure: How a network is traversed mediates expectations about its architecture. Sci. Rep. 7(1):12733.
  36. Pennington J, Socher R, Manning C (2014) Glove: Global vectors for word representation in Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP). pp. 1532–1543.
  37. Newman ME (2003) The structure and function of complex networks. SIAM Rev. 45(2):167–256.
  38. Gómez RL (2002) Variability and detection of invariant structure. Psychol. Sci. 13(5):431–436.
  39. Newport EL, Aslin RN (2004) Learning at a distance I. Statistical learning of non-adjacent dependencies. Cogn. Psychol. 48(2):127–162.
  40. Garvert MM, Dolan RJ, Behrens TE (2017) A map of abstract relational knowledge in the human hippocampal–entorhinal cortex. Elife 6.
  41. Karlaftis VM, et al. (2019) Multimodal imaging of brain connectivity reveals predictors of individual decision strategy in statistical learning. Nat. Hum. Behav. 3:297–307.
  42. Reber AS (1967) Implicit learning of artificial grammars. J. Verbal Learning Verbal Behav. 6(6):855–863.
  43. Mathews RC, et al. (1989) Role of implicit and explicit processes in learning from examples: A synergistic effect. J. Exp. Psychol. Learn. Mem. Cogn. 15(6):1083.
  44. Cleeremans A, McClelland JL (1991) Learning the structure of event sequences. J. Exp. Psychol. Gen. 120(3):235.
  45. Gomez RL, Gerken L (1999) Artificial grammar learning by 1-year-olds leads to specific and abstract knowledge. Cognition 70(2):109–135.
  46. Kahn AE, Karuza EA, Vettel JM, Bassett DS (2018) Network constraints on learnability of probabilistic motor sequences. Nat. Hum. Behav. 2(12):936.
  47. Lynn CW, Kahn AE, Bassett DS (2019) Structure from noise: Mental errors yield abstract representations of events. In revision, Nat. Phys., <arxiv.org/abs/1805.12491 >.
  48. Lynn CW, Papadopoulos L, Kahn AE, Bassett DS (2019) Human information processing in complex networks. Submitted, <arxiv.org/abs/1906.00926>.
  49. Karuza EA, Kahn AE, Bassett DS (2019) Human sensitivity to community structure is robust to topological variation. Complexity 2019.
  50. McCarthy G, Donchin E (1981) A metric for thought: A comparison of p300 latency and reaction time. Science 211(4477):77–80.
  51. Goldstein R, Vitevitch MS (2014) The influence of clustering coefficient on word-learning: how groups of similar sounding words facilitate acquisition. Front. Psychol. 5:1307.
  52. Vitevitch MS, Chan KY, Roodenrys S (2012) Complex network structure influences processing in long-term an d short-term memory. J. Mem. Lang. 67(1):30–44.
  53. Chan KY, Vitevitch MS (2009) The influence of the phonological neighborhood clustering coefficient on spoken word recognition. J. Exp. Psychol. Hum. Percept. Perform. 35(6):1934.
  54. Yates M (2013) How the clustering of phonological neighbors affects visual word recognition. J. Exp. Psychol. Learn. Mem. Cogn. 39(5):1649.
  55. Chan KY, Vitevitch MS (2010) Network structure influences speech production. Cogn. Sci. 34(4):685–697.
  56. Carlson MT, Sonderegger M, Bane M (2014) How children explore the phonological network in child-directed speech: A survival analysis of children?s first word productions. J. Mem. Lang. 75:159–180.
  57. Boas ML (2006) Mathematical methods in the physical sciences. (Wiley).
  58. Howard MW, Kahana MJ (2002) A distributed representation of temporal context. J. Math. Psychol. 46(3):269–299.
  59. Angela JY, Cohen JD (2009) Sequential effects: superstition or rational behavior? in Advances in Neural Information Processing Systems. pp. 1873–1880.
  60. Dehaene S, Meyniel F, Wacongne C, Wang L, Pallier C (2015) The neural representation of sequences: From transition probabilities to algebraic patterns and linguistic trees. Neuron 88(1):2–19.
  61. Meyniel F, Dehaene S (2017) Brain networks for confidence weighting and hierarchical inference during probabilistic learning. Proc. Natl. Acad. Sci. U.S.A. p. 201615773.
  62. Meyniel F, Maheu M, Dehaene S (2016) Human inferences about sequences: A minimal transition probability model. PLOS Comput. Biol. 12(12):e1005260.
  63. Chien HYS, Honey CJ (2019) Constructing and forgetting temporal context in the human cerebral cortex. bioRxiv p. 761593.
  64. Momennejad I, et al. (2017) The successor representation in human reinforcement learning. Nat. Hum. Behav. 1(9):680.
  65. Huettel SA, Mack PB, McCarthy G (2002) Perceiving patterns in random series: dynamic processing of sequence in prefrontal cortex. Nat. Neurosci. 5(5):485.
  66. Cho RY, et al. (2002) Mechanisms underlying dependencies of performance on stimulus history in a two-alternative forced-choice task. Cogn. Affect. Behav. Neurosci. 2(4):283–299.
  67. Falk R, Konold C (1997) Making sense of randomness: Implicit encoding as a basis for judgment. Psychol. Rev. 104(2):301.
  68. Squires KC, Wickens C, Squires NK, Donchin E (1976) The effect of stimulus sequence on the waveform of the cortical event-related potential. Science 193(4258):1142–1146.
  69. Kolossa A, Fingscheidt T, Wessel K, Kopp B (2013) A model-based approach to trial-by-trial p300 amplitude fluctuations. Front. Neurol. 6:359.
  70. Ossmy O, et al. (2013) The timescale of perceptual evidence integration can be adapted to the environment. Curr. Biol. 23(11):981–986.
  71. Wang XJ (2002) Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36(5):955–968.
  72. Honey CJ, et al. (2012) Slow cortical dynamics and the accumulation of information over long timescales. Neuron 76(2):423–434.
  73. Gershman SJ, Moore CD, Todd MT, Norman KA, Sederberg PB (2012) The successor representation and temporal context. Neural Comput. 24(6):1553–1568.
  74. Russek EM, Momennejad I, Botvinick MM, Gershman SJ, Daw ND (2017) Predictive representations can link model-based reinforcement learning to model-free mechanisms. PLoS Comput. Biol. 13(9):e1005768.
  75. Dayan P (1993) Improving generalization for temporal difference learning: The successor representation. Neural Comput. 5(4):613–624.
  76. Jazayeri M, Shadlen MN (2010) Temporal context calibrates interval timing. Nat. Neurosci. 13(8):1020.
  77. Ross SM, et al. (1996) Stochastic Processes. (Wiley New York) Vol. 2.
  78. Holme P, Saramäki J (2012) Temporal networks. Phys. Rep. 519(3):97–125.
  79. Gautreau A, Barrat A, Barthélemy M (2009) Microdynamics in stationary complex networks. Proc. Natl. Acad. Sci. U.S.A. 106(22):8847–8852.
  80. Wang X, McCallum A (2006) Topics over time: A non-markov continuous-time model of topical trends in SIGKDD. (ACM), pp. 424–433.
  81. Starnini M, Baronchelli A, Barrat A, Pastor-Satorras R (2012) Random walks on temporal networks. Phys. Rev. E 85(5):056115.
  82. Amit M, Shmerler Y, Eisenberg E, Abraham M, Shnerb N (1994) Language and codification dependence of long-range correlations in texts. Fractals 2(01):7–13.
  83. Pachet F, Roy P, Barbieri G (2011) Finite-length markov processes with constraints in TwentySecond International Joint Conference on Artificial Intelligence.
  84. Jafari G, Pedram P, Hedayatifar L (2007) Long-range correlation and multifractality in Bach’s inventions pitches. J. Stat. Mech.: Theory Exp. (04).
  85. Lydon-Staley DM, Zhou D, Sizemore Blevins A, Zurn P, Bassett DS (2019) Hunters, busybodies, and the knowledge network building associated with curiosity. Submitted, <psyarxiv.com/undy4>.
  86. Taqqu MS, Teverovsky V, Willinger W (1995) Estimators for long-range dependence: An empirical study. Fractals 3(04):785–798.
  87. Ravasz E, Barabási AL (2003) Hierarchical organization in complex networks. Phys. Rev. E 67(2):026112.
  88. Barabási AL, Albert R (1999) Emergence of scaling in random networks. Science 286(5439):509–512.
  89. Girvan M, Newman ME (2002) Community structure in social and biological networks. Proc. Natl. Acad. Sci. U.S.A. 99(12):7821–7826.
  90. Adamic LA, Lukose RM, Puniyani AR, Huberman BA (2001) Search in power-law networks. Phys. Rev. E 64(4):046135.
  91. Dodds PS, Muhamad R, Watts DJ (2003) An experimental study of search in global social networks. Science 301(5634):827–829.
  92. O’Day VL, Jeffries R (1993) Orienteering in an information landscape: How information seekers get from here to there in Proceedings of the INTERACT’93 and CHI’93 conference on Human factors in computing systems. (ACM), pp. 438–445.
  93. West R, Leskovec J (2012) Human wayfinding in information networks in Proceedings of the 21st international conference on World Wide Web. (ACM), pp. 619–628.
  94. Ding Y (2011) Scientific collaboration and endorsement: Network analysis of coauthorship and citation networks. J. Informetr. 5(1):187–203.
  95. Martin T, Ball B, Karrer B, Newman M (2013) Coauthorship and citation patterns in the Physical Review. Phys. Rev. E 88(1):012814.
  96. Schulz-Hardt S, Frey D, Lüthgens C, Moscovici S (2000) Biased information search in group decision making. J. Pers. Soc. Psychol. 78(4):655.
  97. Jonas E, Schulz-Hardt S, Frey D, Thelen N (2001) Confirmation bias in sequential information search after preliminary decisions: an expansion of dissonance theoretical research on selective exposure to information. J. Pers. Soc. Psychol. 80(4):557.
  98. Cancho RFI, Solé RV (2001) The small world of human language. Proc. R. Soc. Lond., B, Biol. Sci. 268(1482):2261–2265.
  99. Motter AE, De Moura AP, Lai YC, Dasgupta P (2002) Topology of the conceptual network of language. Phys. Rev. E 65(6):065102.
  100. Eriksen KA, Simonsen I, Maslov S, Sneppen K (2003) Modularity and extreme edges of the internet. Phys. Rev. Lett. 90(14):148701.
  101. Arenas A, Fernandez A, Gomez S (2008) Analysis of the structure of complex networks at different resolution levels. New J. Phys. 10(5):053039.
  • aDepartment of Physics & Astronomy, College of Arts & Sciences, University of Pennsylvania, Philadelphia, PA 19104, USA
  • bDepartment of Bioengineering, School of Engineering & Applied Science, University of Pennsylvania, Philadelphia, PA 19104, USA
  • cDepartment of Electrical & Systems Engineering, School of Engineering & Applied Science, University of Pennsylvania, Philadelphia, PA 19104, USA
  • dDepartment of Neurology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA 19104, USA
  • eDepartment of Psychiatry, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA 19104, USA
  • fSanta Fe Institute, Santa Fe, NM 87501, USA C.W.L. and D.S.B. conceived the project, C.W.L. wrote the paper, and D.S.B. edited the paper.
  • 1To whom correspondence should be addressed. E-mail: dsb@seas.upenn.edu. The authors declare no competing financial interests

翻訳抄

話し言葉や音楽といった人間が認知できる刺激ははグラフ構造で表すことができる。人間がどのように時系列のグラフ構造を認識しているかに関する最近の研究をまとめた 2019 年の論文。

  1. Christopher W. Lynn, Danielle S. Bassett (2019) Graph learning: How humans infer and represent networks