消費者行動の理論
 概要
概要
ミクロ経済学は個々の主体が自己利益を最大化する合理的な行動をとるという一貫した前提に基づいて経済現象を説明する。経済活動の善し悪しは消費者一人一人の利益や損失に即して民主的に判断される。経済行動を誘因やインセンティブの観点から理解し、消費者の合理的行動がどのように現われるかを理解することが重要である。この記事では、消費者の合理的行動が消費者の行動に及ぼす影響を分析し、商品の需要がどのように形成されるかを明らかにする。
Table of Contents
 無差別曲線
無差別曲線
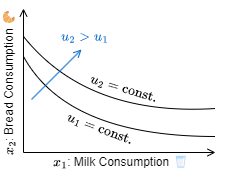
ある財 (商品) 1 と 2 があったとき、それぞれの消費量 \(x_1,x_2\) に対して消費者の効用 (満足度) \(u(x_1,x_2)\) が一定となる点によって構成される曲線を無差別曲線 (indifference curve) または等効曲線と呼ぶ。
 例1. パンと牛乳
例1. パンと牛乳
例えばパンと牛乳があり、パンを減らす代わりに牛乳を飲んで補うことで同じ満足感を得られるとする。しかし牛乳のありがたみはその量が増えるにしたがって鈍化する。最初の一杯目は満足感に大きく作用するが、三杯目、四杯目となるに従ってその作用は小さくなる。言い換えると、一杯目の牛乳はより多くのパンの価値に相当し、牛乳の量が増えるにつれてパンに対する一杯あたりの価値は低くなってゆく。つまりパンで計った牛乳の価値は牛乳の量が多くなると減少する。
このように、価値の減少を考慮して効用 \(u\) が一定となる点を描写すると、効用曲線は一般に Fig 1 に示すような原点に向かって凸の形をした曲線となる。そしてこの曲線の傾きは「パン (第 2 財) で計った牛乳 (第 1 財) の価値」を表している。これを第 2 財に対する第 1 財の限界代替率 (marginal rate of substitution) と呼び \({\rm MRS}_{12}\) で表す。また曲線が右に行くにつれ限界代替率が減少することを限界代替率
パンや牛乳の消費量が多いということはより満腹感をもたらしたり多くの食事をまかなえるということであり、したがって無差別曲線は右上に位置する方がより高い満足感を示している。
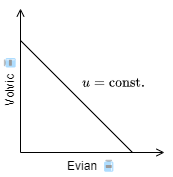
 例2. ミネラルウォーター
例2. ミネラルウォーター
極端な例として、価値が完全に等価と見なされる財では一方の消費を減らした分を他方の消費で補うことで同じ効用を得ることができる。このような財を完全代替財と呼ぶ。例えばミネラルウォーターの銘柄にこだわらない人にとってボルビックとエビアンは同じであるため、ボルビックを減らした量と同じ量のエビアンを飲んでも満足感は同じである。このような完全代替材を無差別曲線として表すと、牛乳で起きたような限界代替率の逓減 (牛乳の対パン価値の減少) はなくなり Fig 2 のような直線となる。
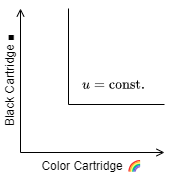
 例3. プリンターカートリッジ
例3. プリンターカートリッジ
もう一つの極端な例として同じ割合で消費しないと効用とならない財がある。このような財を完全補完財と呼ぶ。例えばカラープリンターはカラーとブラックのカートリッジをセットで使わなければならず、ブラックカートリッジだけを多く持っていてもカラーカートリッジの個数より大きい効用を得ることはない (余った分は消費できないので効用に寄与しない)。したがって、無差別曲線は少ない方のカートリッジ数の位置で効用が一定となるように現われ、完全補完財に対する無差別曲線は Fig 3 のような直角の線となる。
 最適消費
最適消費
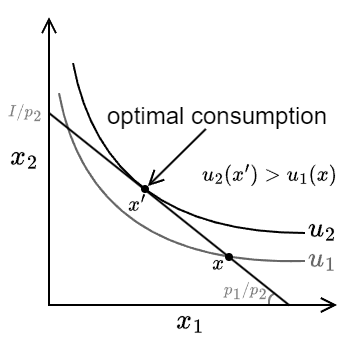
\(n\) 個の財がそれぞれ価格 \(p_1,p_2,\ldots,p_n\) を持つとき、全体の価格体系を \(p=(p_1,p_2,\ldots,p_n)\) と表す。ここである消費者が所得 \(I\) を持っており、各財に対するその消費者の消費計画を \(x=(x_1,x_2,\ldots,x_n)\) とすると、その消費者の購買できる上限を表す予算制約式は式 (\(\ref{budget_constraint_line}\)) のようなベクトルの内積として表すことができる。また予算制約式 (\(\ref{budget_constraint_line}\)) を \(x\) のグラフ空間に表した直線を予算線と呼ぶ。\[ \begin{equation} p_1 x_1 + p_2 x_2 + \ldots + p_n x_n = p x = I \label{budget_constraint_line} \end{equation} \] 消費者にとって合理的な消費行動は制約式 (\(\ref{budget_constraint_line}\)) の下で効用 \(u(x)\) を最大化する消費計画 \(x\) を選ぶことである。この最適消費計画問題を式 (\(\ref{optimal_consumption}\)) のように表す。\[ \begin{equation} \max_{x} u(x) \quad \text{s.t.} \quad p x = I \label{optimal_consumption} \end{equation} \] これは数理計画 (線形計画問題) での式 (\(\ref{optimal_consumption_lp}\)) の定式化と同じである。\[ \begin{equation} \begin{aligned} & \text{maximize} & & f(x) = u(x) \\ & \text{subject to} & & g(x) = p x - I = 0 \end{aligned} \label{optimal_consumption_lp} \end{equation} \] maximize を目的関数、subject to を制約式と呼ぶ。また制約式を満たすすべての変数の組を実行可能解、実行可能解のなかで最も良い目的関数の値を達成するものを最適解、最適解の目的関数値を最適値と呼ぶ。
例として \(n=2\) 財について考える。式 (\(\ref{budget_constraint_line}\)) より、第 2 財の消費計画 \(x_2\) は式 (\(\ref{budget_constraint_line_x2}\)) のような第 1 財の消費計画 \(x_1\) の一次式で表すことができる。\[ \begin{equation} x_2 = - \frac{p_1}{p_2} x_1 + \frac{I}{p_2} \label{budget_constraint_line_x2} \end{equation} \] 予算制約式 (\(\ref{budget_constraint_line_x2}\)) は消費計画 \(x=(x_1,x_2)\) が取り得る値を制限する。最適消費とはその制約の中で効用が最大化する \(x\) である。ここで無差別曲線が原点に凸の形をしており左上に位置するほど効用が高いことを思い出すと、予算制約式 (\(\ref{budget_constraint_line_x2}\)) 上で最も効用が高い点は、予算制約式とある効用曲線が (交差ではなく) 接する点であることがわかる。Fig 4 は予算線と無差別曲線から得られる最適消費の位置を示している。
 限界効用
限界効用
ある財 \(i\) の消費量 \(x_i\) を微調整したときの満足の変化を限界効用 (marginal utility) と呼ぶ。ラグランジュの未定乗数法より、式 (\(\ref{optimal_consumption_lp}\)) のような制約付き最適化問題における極値は式 (\(\ref{lagrange_function}\)) の \(\mathcal{L}\) の各 \(x\) に対する勾配が 0 となる点であることから: \[ \begin{equation} \mathcal{L}(x,\lambda) = f(x) - \lambda g(x) = u(x) - \lambda (p x - I) \label{lagrange_function} \end{equation} \] 式 (\(\ref{lagrange_function_gradient}\)) となるような \(x=(x_1,\ldots,x_n)\) が最適消費計画である。\[ \begin{equation} \forall i \in \{1,\ldots,n\}, \ \frac{\partial \mathcal{L}}{\partial x_i} = \frac{\partial u}{\partial x_i} - \lambda p_i = 0 \quad \Rightarrow \quad \frac{\frac{\partial u}{\partial x_i}}{p_i} = \lambda \label{lagrange_function_gradient} \end{equation} \] ラグランジュ乗数 \(\lambda\) は所得が 1 円増減した時の効用の増減分を表しており所得の限界効用と呼ぶ。式 (\(\ref{lagrange_function_gradient}\)) において \(\lambda\) は財 \(i\) に依存しない定数であることから 1 円の所得増分を追加でどの財の消費に充てたとしても効用は変わらない、つまりこれ以上効用を改善できない最適消費であることを意味している。この式 (\(\ref{lagrange_function_gradient}\)) を限界効用均等の法則と呼ぶ。
 最適消費の性質
最適消費の性質
最適消費計画 \(x'\) は価格体系 \(p\) や所得 \(I\) に依存することから \(x'=x(p,I)\) のように表される。この効用最大化問題から得られる需要 \(x(p,I)\) を需要関数と呼ぶ。
 所得変動の効果
所得変動の効果
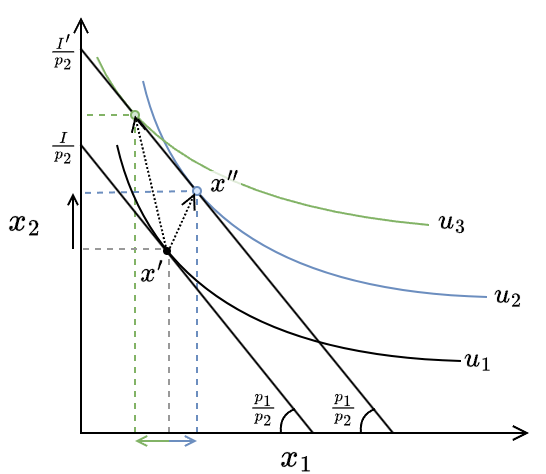
価格体系 \(p\)、所得 \(I\) の予算線が最適消費 \(x'\) で無差別曲線 \(u_1\) に接していると想定する。ここで \(p\) が一定のまま \(I\) が \(I'\) に増加した場合、予算線の傾きは \(-p_1/p_2\) であることから変化はなく切片 \(I/p_2\) のみが増加する (Fig 5)。これにより予算線は右上に平行移動し、より効用の高い無差別曲線 \(u_2\), \(u_3\) と接するようになる。
これは所得が増えると満足度が向上することを表している。消費の増減は所得増加後の無差別曲線により決まる。所得が増えると消費が増える財を上級財または正常財といい、所得が増えると消費が減る財を下級財という。例えば所得の増加により菓子パンの代わりにケーキを食べることが増えたのなら菓子パンは下級財でケーキは上級財である。
 価格変動の効果
価格変動の効果
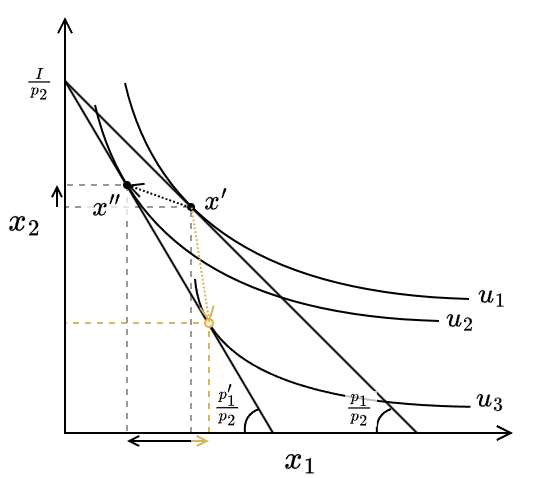
所得 \(I\) が変わらないまま第 1 財の価格が \(p_1'\) に増加した場合、予算線の切片 \(I/p_2\) は変化せずより急な傾き \(-p_1'/p_2\) に変わることから (Fig 6) 予算線はより効用の低い無差別曲線 \(u_2\) と接するようになる。
これは財の価格が上がると満足度が低下することを表しており、一般にはその財の消費が減る方向に作用する。このように価格が上がると需要が減ることは需要法則として知られている。
ただし、理論上は Fig 6 の \(u_3\) のように財の価格 \(p_1\) の上昇により消費 \(x_1\) が増える可能性が存在する。このような特殊な性質の財をギッフェン財と呼ぶ。ギッフェン財は下級財でなければならない。
19 世紀のアイルランドではジャガイモは貧しい人々の主食だった。ある年、ジャガイモの不作によりジャガイモの価格が上昇したところ、贅沢品である肉の消費が減りジャガイモの消費が増えるという現象が起きた。これは第 1 財 (ジャガイモ) の価格が上昇した効果で第 2 財 (肉) に消費が移る作用 (代替効果がマイナス) よりも高価な第 2 財の消費を抑えその分で第 1 財の購入を増やす作用 (所得効果がプラス) が大きかったギッフェン財であるという見方がある。
 補償需要
補償需要
所得 \(I\) が一定であることを想定する需要関数 \(x(p,I)\) に対して、効用 \(u\) が一定の下で最も安上がりな消費計画、つまり費用最小化問題から得られる需要 \(\bar{x}(p,u)\) を補償需要という。式 (\(\ref{compensated-demand}\)) の解は補償需要である。\[ \begin{equation} \begin{aligned} & \text{minimize} & & px \\ & \text{subject to} & & u(x) = \bar{u} \end{aligned} \label{compensated-demand} \end{equation} \]
ある財の価格が上がったとき、その補償需要が増えることは決してない。2 つの価格体系 \(p^0\) と \(p^1\) の下で効用 \(\bar{u}\) を達成する最も安上がりな消費計画 \(\bar{x}^0\) と \(\bar{x}^1\) が存在するとは \(p^1\bar{x}^1 \le p^1\bar{x}^0\) と \(p^0\bar{x}^0 \le p^0\bar{x}^1\) が成り立つことから \((p^1-p^0)(\bar{x}^1-\bar{x}^0) \le 0\) が導かれる。価格が上がったとは \(p^1-p^0 \gt 0\) であるから式 (\(\ref{compensated-demand-change}\)) が成り立ち、補償需要は価格の上昇に対して減少する (または変化しない) ことがわかる。\[ \begin{equation} \bar{x}^1-\bar{x}^0 \le 0 \label{compensated-demand-change} \end{equation} \] 言い換えると \(\delta p_i \gt 0\) に対して \(\delta x_i \le 0\) であるから式 (\(\ref{compensated-demand-derivative}\)) が成り立つ。\[ \begin{equation} \frac{\partial x_i}{\partial p_i} \le 0 \label{compensated-demand-derivative} \end{equation} \] これは自己代替効果は非正となることを表している。
 代替財と補完財
代替財と補完財
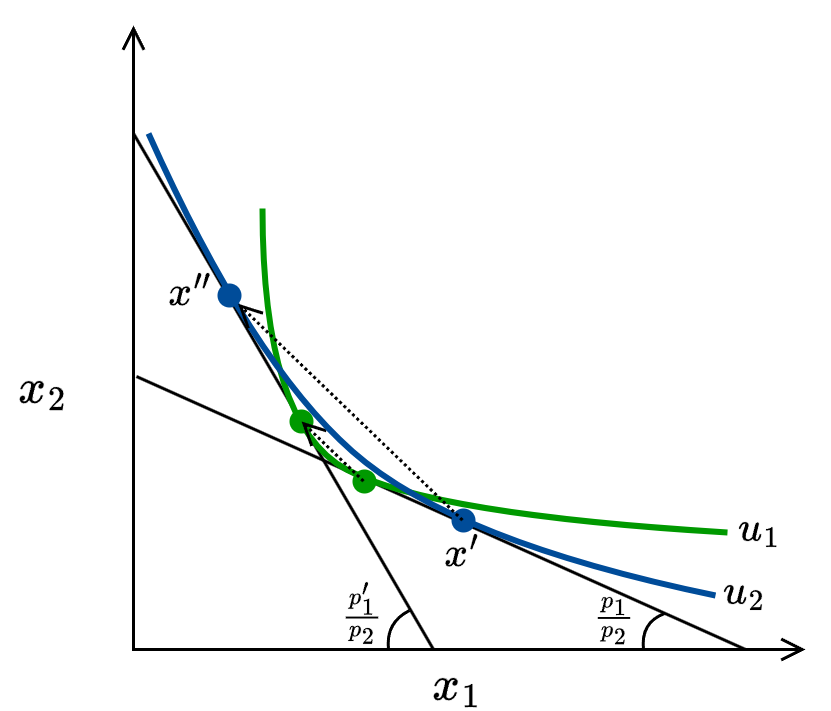
パンと牛乳の例 Fig 1 は完全代替材 Fig 2 と完全補完財 Fig 3 の中間的な無差別曲線と見なすことができる。
完全代替財に近い財は無差別曲線が直線に近く (Fig 7 の \(u_2\))、価格 \(p_1\) の変化に対して消費 \(x_1\) の変化が大きく現われる。完全補完財に近い財 (Fig 7 の \(u_1\)) では逆に価格 \(p_1\) の変化に対して消費 \(x_1\) の変化が小さい。ミネラルウォーターの例では、双方の財は消費者にとって些細な差しかないため小さな価格変動でも消費量の大きな代替が起きやすい。
自己代替効果の非正性により財 \(i\) の価格 \(p_i\) の上昇で需要 \(\bar{x}_i\) が減ったとき、他の財 \(j\) の需要 \(\bar{x}_j\) はどのように変動するだろうか。財の代替性が高ければ他方の \(j\) の需要は増加し、補完性が高ければ \(j\) の需要は減少するはずである。この性質から代替財と補完財を定義することができる。
ある財 \(i\) の価格 \(p_i\) の変動に対する財 \(j\) の補償需要 \(\bar{x}_i\) の変化は \(\frac{\partial \bar{x}_j}{\partial p_i}\) で表されることから、財 \(i\) と \(j\) は \(\frac{\partial \bar{x}_j}{\partial p_i} \gt 0\) であれば代替財であり、\(\frac{\partial \bar{x}_j}{\partial p_i} \lt 0\) であれば補完財であると言える。
 例1. 医療費補助と現金支給
例1. 医療費補助と現金支給
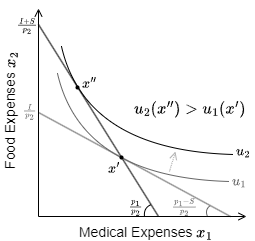
ある消費者の医療消費を \(x_1\)、食料消費を \(x_2\) とする。医療費は \(p_1\) だが、政府による医療費補助 \(S\) により消費者の負担は \(p_1-S\) である。したがって消費者の予算制約式は \((p_1-S)x_1 + p_2 x_2 = I\) となることから予算線は式 (\(\ref{budget_constraint_line_medical1}\)) で表す直線になる。\[ \begin{equation} x_2 = - \frac{p_1-S}{p_2} x_1 + \frac{I}{p_2} \label{budget_constraint_line_medical1} \end{equation} \]
ここで式 (\(\ref{budget_constraint_line_medical1}\)) の最適消費を \(x'=(x_1',x_2')\) とする。
ここで政府が医療費補助の代わりに最適消費と同等の金額をベーシックインカムや年金で現金支給するとどうなるだろうか。式 (\(\ref{budget_constraint_line_medical1}\)) での最適消費の医療費補助分は \(S x_1'\) であることから、この場合の予算制約式は \(p_1 x_1 + p_2 x_2 = I + S x_1'\) であり予算線は式 (\(\ref{budget_constraint_line_medical2}\)) で表す直線になる。\[ \begin{equation} x_2 = - \frac{p_1}{p_2} x_1 + \frac{I + S x_1'}{p_2} \label{budget_constraint_line_medical2} \end{equation} \] この直線は Fig 8 が示すように式 (\(\ref{budget_constraint_line_medical1}\)) より切片が大きく傾きが急である。したがって式 (\(\ref{budget_constraint_line_medical2}\)) の最適消費 \(x''\) はより効用の高い無差別曲線と接することになる。
これは医療費を補助するよりもその最適消費分を現金支給する方が政府の負担は同じで消費者の満足度は高くなることを示唆している。より実生活的な表現では、消費者は以前と同じだけ医療にかかることができるがその分を節約して食事を豪華にすることができるようになっている。「できるのにやらない」とはより良い選択ができるようになったことを示しているため、生活の満足度が上がったことを意味する。
誰の満足も下げずに誰かの満足を上げることをパレート改善と呼ぶ。社会全体のパイが大きくなれば、それをうまく分けることで必ずパレート改善ができる。経済学では、パイが大きくなっているかやパレート改善ができるかという効率性の問題と、パイを童話蹴るかという公平性の問題があり、ミクロ経済は主に効率性の問題を扱う。
 支出関数
支出関数
補償需要関数 \(\bar{x}(p,u)\) に対してある価格体系 \(p\) の下で一定の効用 \(u\) を達成するために最低限必要な金額を (最小) 支出関数と言い式 (\(\ref{expenditure_function}\)) のように表す。\[ \begin{equation} I(p,u) = p \bar{x}(p,u) \label{expenditure_function} \end{equation} \] 支出関数は価格の変動が消費者にもたらす利益や損失を金額として表す。例えば農作物の輸入自由化によって市場価格が下落したときに、農家への補償金はいくらまでなら自由化して利益があったと言えるかといった問題を考えることができる。効用水準 \(u\) は通常観測できないことから代わりに価格に対する支出関数の変動を知ることが重要になる。
式 (\(\ref{expenditure_function}\)) の支出関数を価格で微分すると \(\frac{\partial I(p,u)}{\partial p_i} = x_i = \bar{x}_i(p,u)\) のように補償需要が現われる。これをシェファードの補題と呼ぶ。
 スルツキー方程式
スルツキー方程式
消費者が合理的に行動しているのであれば、ある時点で効用最大化された消費計画、つまり需要関数 \(x(p,I)\) は支出最小化された消費計画、つまり補償需要 \(\bar{x}(p,u)\) と等しい。このような二面性を
スルツキー方程式 (\(\ref{slutsky_equation}\)) の第一項 \(\frac{\partial \bar{x}_i}{\partial p_i}\) は代替効果 (substitution effect) と呼ばれ、第 \(i\) 財の補償需要関数 (最も安上がりに効果を達成できる消費計画) が価格 \(p_i\) の変動に対してどのように反応するかを示しており、価格の変動により消費者が他の財の購入に移行して代替が起こる効果を現している。自己代替効果を示す式 (\(\ref{compensated-demand-derivative}\)) より、代替効果は常に負またはゼロである。
第二項 \(-\frac{\partial x_i}{\partial I}x_i\) の所得効果 (income effect) は、財の価格変動によって相対的に所得の価値が増減したこと (実質所得) による需要量への効果を表している。正常財であれば所得が上がると消費が増える (\(\frac{\partial x_i}{\partial I} \gt 0\)) ことから負、下級財であれば所得が上がると消費が減る (\(\frac{\partial x_i}{\partial I} \lt 0\)) ことから正の値を取る。
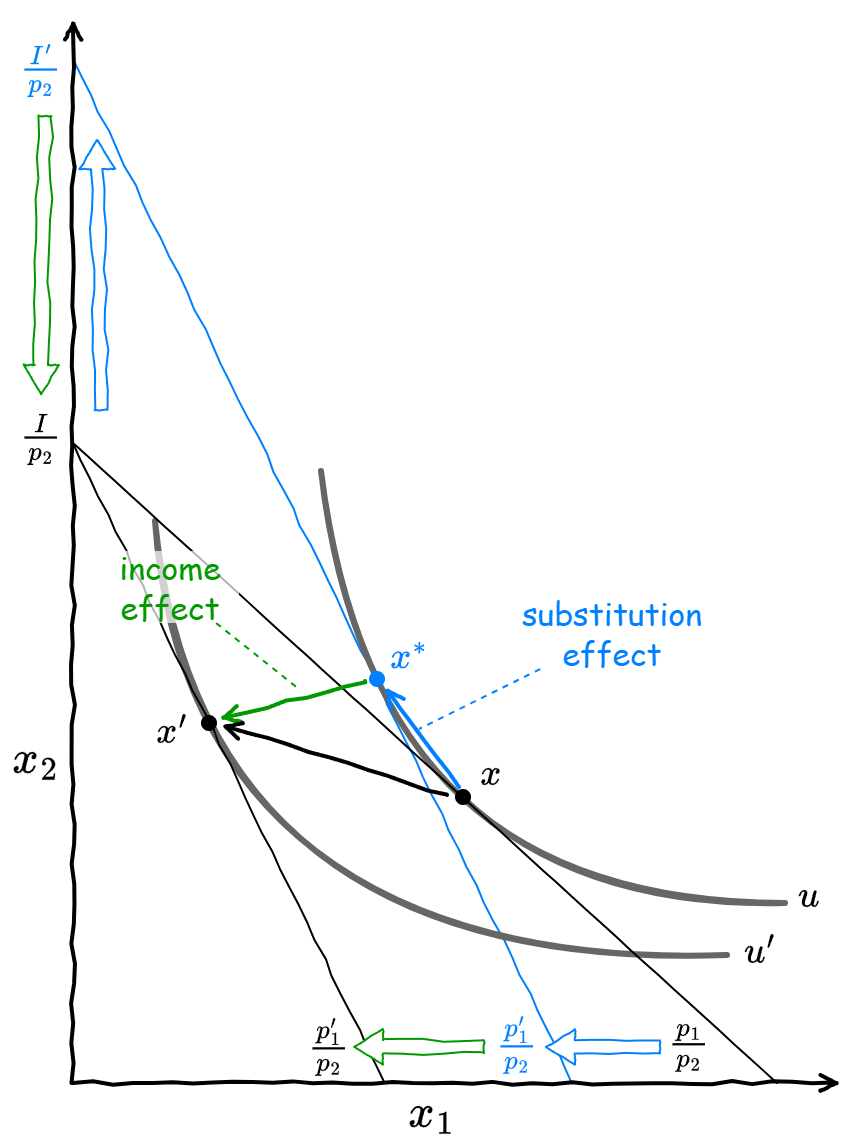
Fig 9 はスルツキー方程式を図で表したものである。第 1 財の価格が \(p_1\) から \(p'_1\) に変動すると予算線の傾きが変化する (\(p' \gt p\) なら傾きはより急になる)。ここで価格変更前と同じ効用 \(u\) を維持しようとすると消費計画を \(x\) から \(x^*\) に変更する必要がある。この変更は価格変動による第 1 財と第 2 財の置き換えを示していることから代替効果である。
さて、代替効果により予算線の \(y\) 軸の切片が \(\frac{I}{p_2}\) から \(\frac{I'}{p_2}\) へ変化している。仮に消費計画を \(x^*\) としたまま消費者に金額 \(I'-I\) を与えれば、消費者は負担も効用も変わっていないことになる。したがってこの \(I'-I\) は価格変動に対する妥当な補償金額と言える。
ただし実際にはそのような補償は行われず消費者の所得は \(I\) のままである。このとき消費者は、傾きが \(\frac{p'_1}{p_2}\) のままで切片が \(\frac{I}{p_2}\) となるような予算線上で最も効用の高い \(u'\) の接点となるように消費計画を \(x^*\) から \(x'\) に変更することになる。これは価格変更前と比べて実質的に所得が \(I'-I\) 減ったのと同じ効果を受ける所得効果である。
最終的にスルツキー方程式の第一項と第二項は、Fig 9 におけるベクトル加算 \(\overrightarrow{x x'} = \overrightarrow{x x^*} + \overrightarrow{x^* x'}\) を表している。
 需要の価格弾力性
需要の価格弾力性
需要の価格弾力性 (price elasticity of demand) とは価格の変動に対して需要がどのように変化するかである。価格の変動 \(\delta p\) に対して需要が \(-\delta x\) だけ変化するとき価格弾力性 \(\varepsilon = \frac{-\delta x/x}{\delta p/p}\) であることから式 (\(\ref{price-elasticity-of-demand}\)) のように表される。\[ \begin{equation} \varepsilon = -\frac{d x}{d p} \frac{p}{x} \label{price-elasticity-of-demand} \end{equation} \] 需要の価格弾力性は、ある時点で価格が 1% 上昇したときに需要がおおよそ何 % 減少するかを示している。\(\varepsilon\) の値が小さいほど価格上昇の影響が小さい財であると言える。
売り上げは \(px\) で表されることから、売り上げの価格に対する変化率は式 (\(\ref{revenue-price-elasticity}\)) のように表すことができる。\[ \begin{equation} \frac{d(px)}{dp} = x + p \frac{dx}{dp} = x \left( 1 - \left(-\frac{dx}{dp} \frac{p}{x}\right) \right) = x \left( 1 - \varepsilon \right) \label{revenue-price-elasticity} \end{equation} \] \(\frac{d px}{dp}\) の傾きは価格変動に対して売り上げがどのように変動するかを表している。したがって:
- \(\varepsilon \lt 1\) のとき、値上げに対して売り上げは増える。
- \(\varepsilon = 1\) のとき、値上げに対して売り上げは変わらない。
- \(\varepsilon \gt 1\) のとき、値上げに対して売り上げは減る。
つまり、需要の価格弾力性 \(\varepsilon\) が小さい財は販売量を制限して価格を上げる高級品路線、\(\varepsilon\) が大きい財は価格を下げて販売量を伸ばす薄利多売路線が合理的と言える。
スルツキー方程式 (\(\ref{slutsky_equation}\)) の両辺に \(-\frac{p}{x}\) を掛けると式 (\(\ref{slutsky-elasticity}\)) のように \(\varepsilon\) を分解することができる。\[ \begin{equation} \varepsilon_i = - \frac{\partial x_i}{\partial p_i} \frac{p_i}{x_i} = - \frac{\partial \bar{x}_i}{\partial p_i} \frac{p_i}{\bar{x}_i} + \left( \frac{\partial x_i}{\partial I} \frac{I}{x_i} \right) \left( \frac{p_i x_i}{I} \right) \label{slutsky-elasticity} \end{equation} \] ここで右辺第一項は補償需要の価格弾力性、第二項は需要の所得弾力性 ✕ 支出中で第\(i\)財が占める割合である。したがって需要の価格弾力性 \(\varepsilon\) はつぎのように変動する:
第一項は密接な代替財があるとき上昇する。ミネラルウォーターの例では安易に他の商品に乗り換えることができるため、ボルビックやエビアンは値上げに対して消費が落ちやすい。これは前述のように完全代替財に近い財は価格の変化に対して消費の変化が大きく現われることを意味する。
第二項左は所得の増減が消費に影響を受けやすい財のとき上昇する。価格の上昇は実質的な所得の減少と同義であるため、所得の増減に敏感な財は価格上昇に対しても消費が落ちやすい。
第二項右はその財の支出が所得全体の中で大きく占めているのとき上昇する。そのような財は 1% の上昇であっても家計に与える影響が大きいことから価格上昇に対して消費が落ちやすい。
 例5. 最適消費を求める例
例5. 最適消費を求める例
2 つの財 1, 2 それぞれの消費量を \(x_1\), \(x_2\)、所得を \(I\) としたとき、効用関数 \(u(x_1,x_2) = x_1^{c_1} x_2^{c_2}\) を持つ消費者の両財に対する最適消費を求める。ここで \(c_1\), \(c_2\) は正の定数とする。
これは予算制約 \(p_1 x_1 + p_2 x_2 = I\) の下で \(u(x_1,x_2)\) を最大化する問題であることから、ラグランジュの未定乗数法を用いると: \[ \mathcal{L} = x_1^{c_1} x_2^{c_2} - \lambda (p_1 x_1 + p_2 x_2 - I) \\ \left\{ \begin{aligned} \frac{\partial \mathcal{L}}{\partial x_1} & = c_1 x_1^{c_1 - 1} x_2^{c_2} - \lambda p_1 = 0 \\ \frac{\partial \mathcal{L}}{\partial x_2} & = c_2 x_1^{c_1} x_2^{c_2 - 1} - \lambda p_2 = 0 \\ \end{aligned} \right. \] より式 (\ref{ex5_ratio}) が得られる。\[ \begin{equation} \therefore \frac{c_1}{c_2} = \frac{p_1 x_1}{p_2 x_2} \label{ex5_ratio} \end{equation} \] これは、この例においては所得 \(I\) の中で財 1 と財 2 の支出比 \(p_1x_1:p_2x_2\) が \(c_1:c_2\) となるような消費が最適消費であることを意味している。それぞれの支出 \(\frac{c_1}{c_1+c_2}I=p_1x_1\) と \(\frac{c_2}{c_1+c_2}I=p_2x_2\) より最適消費は式 (\ref{ex5_optimal}) のように表される。\[ \begin{equation} \left\{ \begin{aligned} x_1 & = \frac{c_1}{c_1 + c_2} \frac{I}{p_1} \\ x_2 & = \frac{c_2}{c_1 + c_2} \frac{I}{p_2} \\ \end{aligned} \right. \label{ex5_optimal} \end{equation} \]
この例は「所得の何割を特定の財の消費に充てると効用が最も高くなるか」が分っているようなモデルを表している。例えば住宅ローンの返済は手取りの 20% が目安とされている。手取り年収 1000 万円の人であれば年 200 万円であることは容易に計算できるが、この例から財 1 をローン返済、財 2 をそれ以外の消費としたとき、このモデルの効用関数は \(u(x_1,x_2) = x_1^{20} x_2^{80}\) と表すことができることがわかる。
 参考文献
参考文献
- 神取道宏. ミクロ経済学の力. 日本評論社, 2014.