ミクロ経済学

企業行動の理論

Takami Torao
  • このエントリーをはてなブックマークに追加

概要

企業は市場経済における主要な経済主体の一つである。企業の行動は市場の価格や生産量などの経済変数に影響を与え、市場の機能や効率性に大きな影響を及ぼす。その動機は利益最大化であり、生産、価格設定、競争戦略などのさまざまな活動を通じてその目標を実現しようとする。本章では、企業の行動に焦点を当て、企業の意思決定が市場経済に及ぼす影響を考える。

企業内部の経済活動は経営学の範疇であり、制度や規則、慣習などの下で遂行されていて経済学の市場メカニズムとは本質的に異なる力が働いている。古典的なミクロ経済、価格理論では企業を生産要素を導入すると生産物を生み出すブラックボックスとして扱う。

Table of Contents

  1. 概要
  2. 生産関数
  3. 利潤最大化
    1. 費用関数と供給曲線
      1. 標準的なケース
  4. 参考文献

生産関数

市場から企業への労働や資材といった投入 \(L\) した結果としてもたらされる生産量を \(y\) としたとき、達成可能な生産の集まりを生産可能性集合 (product possibility set) と言う。また投入に対して達成可能な生産の最大量からなる線を生産関数 (production function) と呼び \(y=f(L)\) のように表す。

Fig 1 でグレーで表されている領域が生産可能性集合で、その縁となる曲線が生産関数を表している。ここで生産 \(A\) は投入に対して生産を上げる余地があり非効率的である。生産 \(B\) は投入に対して達成可能な上限にあり効率的と言える。

生産関数
Fig 1. 生産関数 \(y=f(L)\) と生産可能領域。

労働の生産性は労働投入あたりの生産量 \(\frac{f(L)}{L}\) で表し労働の平均生産性と言う。また労働投入に対する生産量の変化は \(\frac{df(L)}{dL}\) で表される。これを労働の限界生産性と言う。生産工場では通常、効率の良い方法や機械を優先して使用してゆくためその限界生産性は次第に落ちてゆく。一般には Fig 1 のように、労働投入が少ないときは労働の限界生産性は高いが、労働投入が増加してゆくと効率が落ちて労働の限界生産性は下がる傾向にある。これを限界生産性逓減の法則と言う。

ミクロ経済では (生産機械などを含む) すべての生産要素の量を変えることができる期間を長期といい、一部の生産要素の量が固定されている期間を短期と言う。

利潤最大化

市場に多数の生産者、消費者が存在し、個々の生産者や消費者が生産や消費を変えても市場で成立している価格や需要に影響がない状態を完全競争という。また個々の生産者や消費者が「市場価格は一定」と想定して行動することをプライステイカーの仮定と言う。

価格 \(p\) と労賃 \(w\) が一定で (つまりプライステイカー仮定の下で) 完全競争的な環境における企業の利潤最大化問題は式 (\(\ref{pfmax}\)) のように表される。\[ \begin{equation} \max_{L} p f(L) - wL \label{pfmax} \end{equation} \] 利潤を \(\pi = pf(L) - wL\) とすると \(f(L) = \frac{w}{p}L + \frac{\pi}{p}\) が成り立つ。これは \(L\) についての一次線形の直線である。

費用関数と供給曲線

標準的なケース

標準的なケースとは、生産関数が Fig 1 で示すような上に凸で固定費がすべてサンクコストの場合とする。

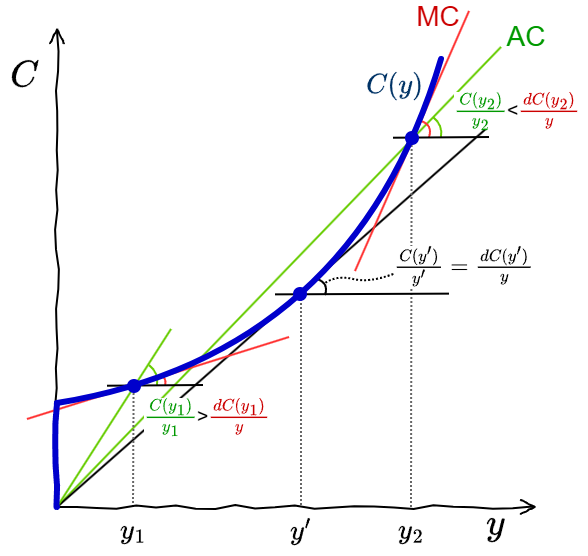
  • 生産 1 単位あたりの費用 \(\frac{C(y)}{y}\) を平均費用 (AC; average cost) と言う。平均費用は、ある生産に対する総費用 \(C(y)\) の原点からの傾きを表している。

    標準的なケースでは費用関数 \(C(y)\) は下に凸の形をしていることから、平均費用は一度下がり、費用関数が原点との直線で接する点 \(y'\) で最小値を取り、それ以降は上昇する。つまり平均費用は生産 \(y\) に対して U 字型の曲線を描く。

  • 生産物を限定的に増やすために必要な費用、つまり費用関数の微分 \(\frac{dC(y)}{dy}\) を限界費用 (MC; marginal cost) と言う。

    限界費用は生産量 \(y\) に対して単調増加する。ただし労働の限界生産性の逓減よりその増加速度は \(y\) が大きくなるほど鈍くなる。

Fig 1. 平均費用と限界費用の関係。

利潤は生産物によって得られた利益 \(py\) から費用 \(C(y)\) を引いたものである。つまり利潤最大化問題は式 (\(\ref{profitmax}\)) となるような \(y'=S(p)\) を求めることである。\[ \begin{equation} \max_{y} py - C(y) \label{profitmax} \end{equation} \] この \(S(p)\) を供給関数と呼び、その曲線を供給曲線と言う。標準的なケースでは供給曲線は限界費用曲線に等しい。

限界費用は費用に対する生産量の微分であることから、供給関数の生産量に対する積分は費用を表す。価格 \(p\) の下で生産 \(y\) を行ったときの収入は \(p \times y\) であるため、これより供給関数の積分を引いたものが利潤となる。生産者余剰はサンクされた固定費を差し引く前の利潤のことである。

参考文献

  1. 神取道宏. ミクロ経済学の力. 日本評論社, 2014.