論文翻訳: Characterizing Reference Locality in the WWW
(virgilio@bu.edu)
(best@bu.edu)
(crovella@bu.edu)
(dri@dcc.ufmg.br)
 ABSTRACT
ABSTRACT
本論文では、Web サーバに到来するリクエストストリームにおける時間的局所性と空間的局所性の両方を考慮したモデルを提案する。文書の人気度のみに基づく単純なモデルでは、時間的局所性あるいは空間的局所性のいずれをも十分に捉えられないことを明らかにする。代わりに、我々は参照ストリームの数値的表現であるスタック距離トレースに着目する。時間的局所性はスタック距離トレースの周辺分布によって特徴付けられることを示し、典型的な分布パターンに基づくモデルを提案した上で、それらのキャッシュ性能を実際のトレースデータと比較検証する。さらに、参照ストリームにおける空間的局所性を自己相似性の概念を用いて特徴付けられることを示す。自己相似性とは、データセット内に存在する長距離相関を記述する特性であり、従来の研究では合成参照列に組み込むことが困難とされてきたものである。本研究では、スタック距離列が強く自己相似性を示すことを実証し、我々のトレースデータにおける自己相似性の度合いについて詳細な測定結果を提示する。最後に、本研究で測定した時間的局所性と空間的局所性の特性を忠実に再現する合成Webトレースを生成するための手法について考察する。
Table of Contents
 1 導入
1 導入
参照の局所性原理は、コンピュータシステム設計において極めて重要な意味を持つ。時間的局所性 (temporal locality) を示す参照ストリームはキャッシュ機構の恩恵を受けることができ、空間的局所性 (spatial locality) を示すストリームはプリフェッチ機構の効果を享受できる。これらの原理の応用例 (例えばメモリシステムにおける実装) については十分に研究がなされている [10, 23]。
World Wide Web (Web) のキャッシュシステムおよびプリフェッチシステムの設計にこれらの原理を適用するためには、典型的な Web 参照ストリームに存在する局所性の度合いを特性評価することが不可欠である。Web アクセスにおける時間的局所性とは、あるアイテムが過去に頻繁にアクセスされた場合、将来的にもアクセスされる可能性が高いという性質を指す。一方、空間的局所性とは、過去に頻繁にアクセスされたアイテムに隣接する (neighboring) アイテムも、将来的にアクセスされる可能性が高いという性質を意味する。メモリシステムにおいては、このような隣接関係 (neighborhoods) はアドレス空間上の近接性という観点から容易に定義可能であり、これがキャッシュラインやメモリページといったプリフェッチ対象の単位を生み出す要因となっている。Web システムの場合、空間的局所性を適切に特性評価できれば、同様のプリフェッチ対象を特定することが可能であると考えられる。
これまでの研究において、記号参照ストリームの局所性特性に関して、参照ストリームを同等の数値表現に変換することの有効性が示されている。具体的には、スタック距離ストリーム (stack distance stream) [19] がその代表例である。この変換処理は、元のトレース情報の全てを保持しつつ、具体的な参照名のみを削除するため、可逆的である。これにより、元のトレースを再構築することが可能となる (ただし再構築されたトレースには人工的な名称が付与される)。スタック距離ストリームには周辺分布 (marginal distribution) と相関構造 (correlation structure) [19, 22] という 2 つの重要な特性があり、これらを用いて時間的局所性と空間的局所性を定量的に評価できる。周辺分布は、ストリーム内で同一オブジェクトへの 2 つの参照が、何らかの中間参照によってどの程度分離されているかの確率を測定する。一方、ストリームの相関構造は、過去の参照ストリームに基づいて将来の参照を予測できる可能性の度合いを測定するものである。
本論文では、スタック距離に基づく定量的手法を用いて、Web 参照ストリームの時間的局所性と空間的局所性の特性を測定する。具体的には、4 つの Web サーバで収集した参照ストリームを分析し、スタック距離の周辺分布 (すなわち時間的局所性) に関するモデルを提案するとともに、関連するパラメータの典型的な値範囲を明らかにする。さらに、スタック距離の相関構造に基づいて、参照ストリームの空間的局所性を記述するモデルも提案する。これらの測定結果を用いて、任意の長さの合成参照ストリームを生成する方法を示し、その性能特性が実測データの特性を忠実に再現できることを実証する。
本手法の新規性は、統計的自己相似性 (statistical self-similarity) を利用して参照ストリームの相関構造を捉える点にある。すなわち、Web 参照ストリームが統計的自己相似性を示すことを明らかにし、この特性が空間的局所性に起因する参照ストリームの諸特性を説明する上で有効であることを実証する。参照ストリームに自己相似性が存在することは、オブジェクト参照間の相関が極めて多様な時間スケールで発生し得ることを意味する (長距離依存性 (long-range dependence))。長距離依存性を示す時系列データは、短期依存性あるいは依存性が全くない時系列データと比較して、はるかに「バースト的」な性質を示す。これは、一般的に観察される参照局所性の特性と一致する。スタック距離時系列における長距離依存性はまた、キャッシュミスパターンに見られる既知のフラクタル特性 [26] とも関連しており、我々はこれまでのフラクタル参照パターンに関する研究結果を、本研究の知見に基づいて再解釈する。
この空間局所性の測定手法は、参照ストリームが数値ではなく記号で構成されている場合においても、空間局所性の概念に対する新たな解釈を提供する。オブジェクト \(A\) がオブジェクト \(B\) に近いと判断される条件は、\(A\) への参照が \(B\) への参照直後に高い確率で発生する場合である。すなわち、オブジェクト間の距離は、第一次マルコフ連鎖として考慮したオブジェクト参照の遷移確率の逆数で定義される。この定義は通常考えられるノルムの概念には該当しない (対称性を持たない) ものの、プリフェッチ処理における空間局所性の重要な特性 ― すなわちプリフェッチが成功する可能性 ― を適切に捉えている。
本手法では、文書サイズを考慮せずに参照ストリームの局所性特性に着目する。このため、シミュレーションにおいてはキャッシュ容量を固定データ量ではなく一定の文書数を保持できるサイズとして設定している。この仮定は、我々が関心を持つ局所性という特性が、いかなるキャッシュサイズにも依存しない参照ストリームの本質的な性質であるためである2。
本節の残りの部分では、本研究の測定データおよびトレースシミュレーションの基礎となるデータについて述べる。セクション 2 では、Web 文書の人気度特性を特徴付け、人気度に基づくキャッシュ参照モデルでは、実際の Web トレースに見られる参照特性の時間的・空間的局所性を十分に表現できないことを明らかにする。これらの参照特性に関する証拠はセクション 3 で提示する。セクション 4 およびセクション 5 では、これらの特性を詳細に特徴付け、これらの特性を捉える統計モデルを提案する。セクション 6 では関連研究について考察する。最後にセクション 7 では、本研究の総括と今後の研究方向について述べる。
データ収集: Web はクライアント・サーバー型アーキテクチャを基盤とした大規模分散情報システムである。したがって、サーバー側から観測される処理負荷は、多数の異なるクライアントから発信されるリクエストの集合体として現れる。参照局所性を分析するため、国立スーパーコンピューティング応用センター (NCSA) 設置の NCSA Web サーバー、サンディエゴ・スーパーコンピュータセンター (SDSC) 設置の SDSC Web サーバー、ノースカロライナ州リサーチ・トライアングル・パーク所在の EPA Web サーバー、ボストン大学コンピュータサイエンス学部 (BU) 設置の Web サーバーの 4 種類の Web サーバーのアクセスログを調査した。NCSA のデータに関しては、対象は単一のサーバー (Costello) のみである。SDSC および EPA のログデータはインターネット・トラフィック・アーカイブ [14] で公開されている。NCSA のログデータは現地スタッフへの問い合わせにより取得し、BU のログデータは学部内の Web サーバーから直接収集した。
各ログファイルには、サーバーが処理した各リクエストごとに 1 行の情報が記録されている。各行には、リクエストを送信したホスト名、リクエストが送信されたタイムスタンプ、要求されたオブジェクトのファイル名、および応答データのバイトサイズが含まれている。Table 1 に、これら 4 種類の Web サーバーのログに関する統計情報を要約する。
| ログ | NCSA | SDSC | EPA | BU |
|---|---|---|---|---|
| 期間 | 1 日 | 1 日 | 1 日 | 2週間 |
| 開始日 | 1995年12月 | 1995年8月 | 1995年8月 | 1995年10月 |
| 総リクエスト数 | 46,965件 | 28,338件 | 47,748件 | 80,518件 |
| ユニークリクエスト数 | 4,891件 | 1,267件 | 6,318件 | 4,471件 |
- 2先行研究 [9] において、文書サイズと参照頻度の期待値との間に相関関係があることを実証している。この前提条件は、キャッシュ性能分析を直接的に適用する上でやや制約要因となる。このため、我々は現在この研究を拡張し、分析対象に文書サイズを含める作業を進めている。それにもかかわらず、現行の手法は Web 参照ストリームの空間的局所性と時間的局所性の両方を簡潔かつ効果的に捉える有効な手段であると確信している。
 2 Web 文書の人気度特性分析
2 Web 文書の人気度特性分析
Web 文書の人気度に著しい偏りが見られる現象は、従来から十分に研究されており、キャッシュ管理、複製戦略、情報拡散に関する既存研究でも広く活用されている。これらの研究において「人気のあるファイルは極めて人気が高い」ことが実証されている [4, 13]。[9] では、Cunha, Bestavros, Crovella がクライアントから要求される Web 文書の人気度特性を分析し、Web 文書に対しても Zipf の法則[27, [17] で議論されている) が成立することを確認した。Zipf の法則は本来、単語の人気度 (順位) と使用頻度の関係に適用された経験則である。具体的には、特定のテキスト中で使用される単語の人気度を使用頻度3 (\(P\) と表記) でランク付けした場合、\[ P \sim 1/\rho \] という関係が成り立つ。この分布はパラメータを持たない双曲線分布であることに注意。すなわち、\(\rho\) は正確に \(-1\) の冪乗とされ、これにより \(n\) 番目に人気のある文書は、\(2n\) 番目に人気のある文書と比較して、アクセスされる確率が正確に 2 倍となる。
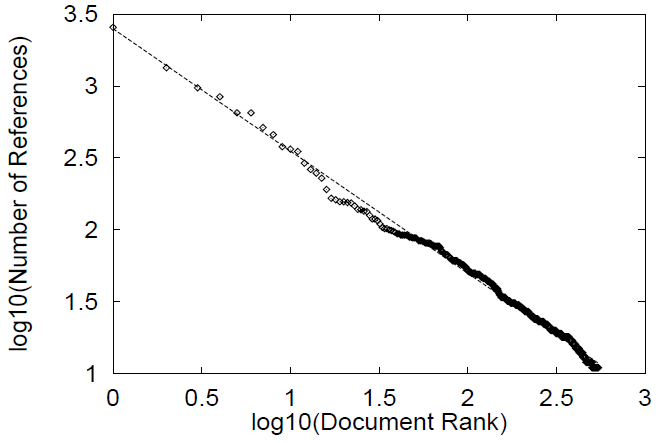
本研究のデータによれば、Zipf の法則はWeb サーバーが提供する Web 文書に対して極めて強く適用されることが確認される。この結果は Figure 1 に示されており、BU トレースで観測された全 2135 文書について分析した結果である。図は、各文書に対する参照回数の総数 (Y軸) を、文書の総合的人気度における順位 (X軸) の関数として対数-対数プロットしたものである。直線への適合度は非常に高く (\(R^2=0.99\))、直線の傾きも \(-0.85\) と明確である (図中で示されているとおり)。したがって、Web 文書における人気度と順位の関係を表す指数は、Zipf の法則が予測する \(-1\) に極めて近い値となっている。
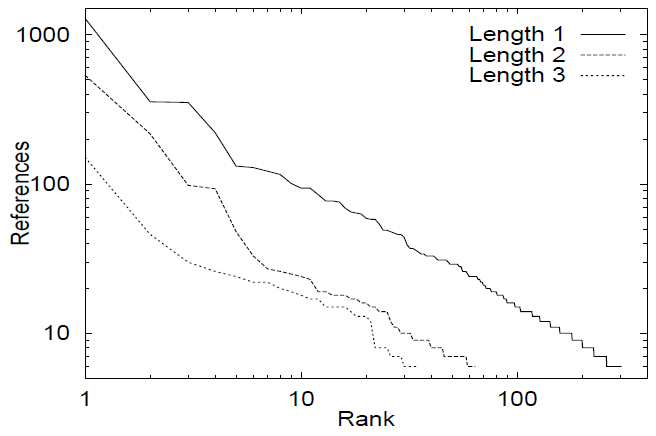
我々の測定結果によれば、Zipf の法則は文書の単一リクエストだけでなく、リクエストストライド (strides; 連続パターン) にも適用されることが示唆される。リクエストストライドとは、同一クライアントからの連続リクエストの系列を指し、その系列内における連続リクエスト間の時間間隔が所定のストライド閾値を超えない場合を指す。Figure 2 は、長さ \(k=1,2,3\) のストライドに対する総参照回数 (Y軸) を、ストライドの全体的な人気度順位 (X軸) の関数として、対数-対数プロットで示したものである。このプロットに使用したデータは BU トレースであり、ストライド閾値は 10 秒に設定されている。Figure 2 に示す曲線群と直線との適合度の高さ (傾きが \(-1\) に近い値を示すこと) は、ジップの法則がリクエストの連続パターンにも確かに適用されることを示唆している。
上述の観察結果を踏まえると、文書アクセスモデル [12, 2] の一つとして、文書の人気度プロファイルに基づいて文書要求を生成する方法が考えられる。このモデルを Zipf 分布ベースモデル (Zipf-based model) と呼ぶ。このモデルの妥当性を検証するため、BU で観測された文書の人気度プロファイルを満たすように人工的に生成した要求に対して、サーバでのミス率を測定した。さらに、実際の BU トレースを用いてシミュレーションを実行した場合の測定結果と比較した。人工トレースは、BU の実際のトレースにランダムな順列を適用することで生成した。この比較結果を Figure 3 に示す。
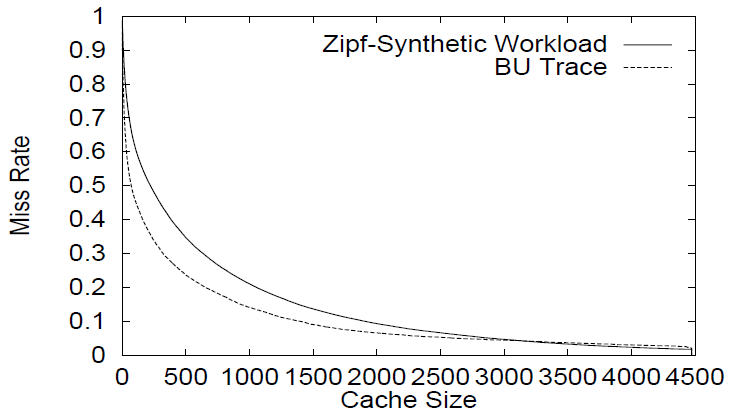
明らかに、Web 文書のキャッシュモデルにおいて人気度を基本要素として用いることは、満足のいく結果をもたらさない。Figure 3 が示すように、キャッシュサイズが 400 アイテムの場合、ジップ分布ベースのキャッシュモデルによるミス率は、実際のミス率に比べて約 33% も低い値となる。
Zipf 分布ベースモデルの主な欠点は、実際のトレースに存在する可能性のある参照局所性特性を捉えられない点にある。特に、このモデルは文書の一般的な人気度プロファイルは保持するものの、時間的・空間的な参照局所性特性を捉えることができない。次節では、これらの特性が実際に Web トレースに存在することを示す証拠を提示し、セクション 4 およびセクション 5 では、これらの特徴を簡潔かつ表現力豊かに記述する統計モデルを提案する。
- 3ジップの法則はその後、社会科学分野における他の人気度事例にも適用されている [27]。
 3 参照局所性の根拠
3 参照局所性の根拠
時間的局所性: 時間的局所性とは、最近アクセスされた文書は近い将来に再び参照される可能性が高いという性質を指す。[19, 24] で提案された概念に基づき、我々は要求ストリーム内に存在する時間的局所性関係を捉えるスタック距離モデルを定義する。ここで、参照ストリーム \(R_t = r_1,r_2,\ldots,r_t\) を考える。ここで \(r_t\) は仮想時間 \(t\) において要求されたオブジェクトの名称を表す。我々の時間単位は \(1\) 要求とし、仮想時間 \(t\) はこれまでに \(t\) 個の要求がサーバに到達したことを意味する。さらに、LRU スタック \(S_t\) を定義する。これは、サーバ上の全オブジェクトを使用頻度の新しさに基づいて順序付けたものである。したがって、仮想時間 \(t\) tにおける LRU スタックは以下のように表される: \[ \begin{equation} S_t = \{o_1,o_2,\ldots,o_N\} \label{eq1} \end{equation} \] ここで \(o_1,o_2,\ldots,o_N\) はサーバ上のオブジェクトであり、\(o_1\) は最も最近アクセスされたオブジェクト、\(o_2\) はその次に最近参照されたオブジェクト、といった具合である。もし \(o_1\) が最も最近アクセスされた文書であるならば、\(r_t=o_1\) となる。オブジェクトへの参照が行われるたびに、スタックは更新されなければならない。\(r_{t+1}=o_1\) であると仮定すると、スタックは \(S_{t+1}=\{o_i,o_1,o_2,\ldots,o_N\}\) となる。今、\(S_{t-1}=\{o_1,o_2,\ldots,o_N\}\) かつ \(r_t=o_i\) であると仮定しよう。この場合、要求 \(r_t\) はスタック \(S_{t-1}\) において距離 \(i\) に位置すると言える。時刻 \(t\) において参照された文書のスタック距離を \(d_t\) と表記する。このとき、以下の関係が成り立つ: \[ \begin{equation} \text{if } r_t = o_i \text{ then } d_t = i \label{eq2} \end{equation} \] このように、任意の要求列 \(R_t=r_1,r_2,\ldots,r_t\) に対して、対応する距離列 \(\delta=d_1,d_2,\ldots,d_t\) が存在する。したがって、距離列と要求列は参照情報の観点から同等とみなすことができる。距離列は Web ユーザがサーバから文書を要求する際のパターン (実際の文書内容ではなく) を反映しているため、これをオブジェクト参照パターンのモデルとして採用する4。
距離確率の周辺分布は、同一対象物への 2 つの参照間に存在する中間参照の数を測定するものであるため、時間的局所性の指標となる。スタック距離が短い場合、それは文書への頻繁な参照が行われていることを示している。言い換えれば、最も頻繁に参照される文書は、スタックの上部付近に位置している傾向が強い。
我々のトレースデータにおける時間的局所性の度合いを評価するため、BU トレースで観測された平均スタック距離と、同じトレースをランダムに並べ替えたスクランブルトレースの平均スタック距離を比較した。その結果を Table 2 に示すが、スクランブルトレースの方が平均スタック距離が明らかに大きいことが確認され、これは時間的局所性が低下していることを意味している。
| BU トレース | オリジナル | スクランブル済み |
|---|---|---|
| 平均スタック距離 | 479.798 | 645.586 |
| 標準偏差 | 941.430 | 968.840 |
空間的局所性: 参照の空間的局所性の存在を確認するためには、トレース内で実際に観測された固有の参照系列の総数と、そのトレースをランダムに並べ替えた場合に得られる固有の参照系列の総数を比較すればよい。注意すべき点として、トレースのランダムな並べ替え (以下スクランブルトレースと呼ぶ)は、そのトレース内の各文書の人気度プロファイルを保持するものの、参照系列間の相関関係を破壊するため、元のトレースに存在していた可能性のある空間的局所性を消失させることになる。もし参照が実際に相関しているのであれば、トレース内で観測される固有の参照系列の総数は、スクランブルトレースで観測される総数よりもはるかに少なくなることが予想される。
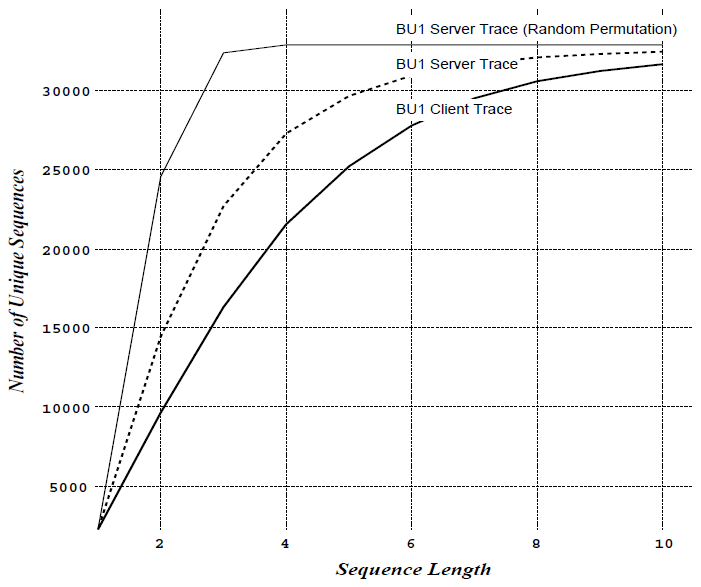
Figure 4 に、BU トレースの最初の 1 週間 (最初の 32,839 件の参照データ) において観測された、長さ \(k\) の固有シーケンスの総数 (Y軸) を示す。このデータセットを BU1 サーバートレースと呼ぶ。3 つのケースを示している。最上部の曲線は、乱数化処理を施した BU1 トレースにおいて観測された長さ \(k\) の固有シーケンスの総数を表している。中央の曲線は、元の BU1 トレースで観測された長さ \(k\) の固有シーケンスの総数を示している。サーバーに送信されるトレースは複数の個別クライアントトレースの混在を反映しているため、最下部の曲線では、BU1 トレース内の各個別クライアントを個別に考慮した場合に観測される長さ \(k\) の固有シーケンスの総数をプロットしている。
3 つの曲線はいずれも、\(k\) の値が大きくなるにつれて固有シーケンスの総数が増加する傾向を示している5。ランダム化されたトレースが最も急激な増加を示し、クライアントトレースが最も緩やかな増加を示している。これらの結果は、クライアントアクセスパターンにおいて顕著な空間的局所性が存在することを裏付けている。例えば、乱数処理を施した BU1 トレースでは長さ 3 のシーケンスが最大 32,327 種類観測されるのに対し、BU1 クライアントトレースでは長さ 3 のシーケンスが 16,114 種類しか観測されない (これは50%以上の減少率に相当する)。この空間的局所性はある程度「希薄化」されているものの、BU1 サーバートレースにおいても依然として明確に確認できる。具体的には、BU1 サーバートレースでは長さ 3 のシーケンスが 22,680 種類観測されており (これは約 30% の減少率に相当)、これはクライアントトレースの場合よりもさらに顕著である。
- 4スタック順序アルゴリズムとして LRU を採用したことは、本手法の適用範囲を特定のキャッシュ戦略に限定するものではない。しかしながら、これにより LRU キャッシュを本手法の精度検証手段として直接評価することが可能となる。この検証作業については第4節で詳細に述べる。
- 53 つの曲線がすべて横ばいになる現象は、トレースの長さに制限があることに起因している。特に、長さ \(l\) のトレースにおいては、\(l-k\) 種類を超える長さ \(k\) の固有シーケンスを観測することは不可能である。本実験では \(l=32,839\) を採用しているため、これが観測された上限値となっている。
 4 時間的局所性の特徴付け
4 時間的局所性の特徴付け
実際のトレースとスクランブル処理を施したトレースでは、そのスタック距離トレースの集約特性に明確な差異が見られることから、本研究ではスタック距離の周辺分布について詳細に分析する。
セクション 1 で述べたように、スタック距離の周辺分布はトレースに内在する時間的局所性を反映している。具体的には、スタック距離に対応する確率変数 \(D\) とその分布関数 \(F_D\) が与えられた場合、また \(C\) ファイルを保持可能なキャッシュのミス率 \(M(C)\) (スタック距離トレース生成時に使用した置換アルゴリズムと同じものを使用する) を定義すると、以下の関係が成り立つ: \[ P[D \gt C] = 1 - F_D(C) = M(C) \] したがって、補数分布関数 \(1-F_D\) の知識があれば、与えられたトレースに対して任意のサイズのキャッシュの性能を予測するのに十分な情報が得られる。
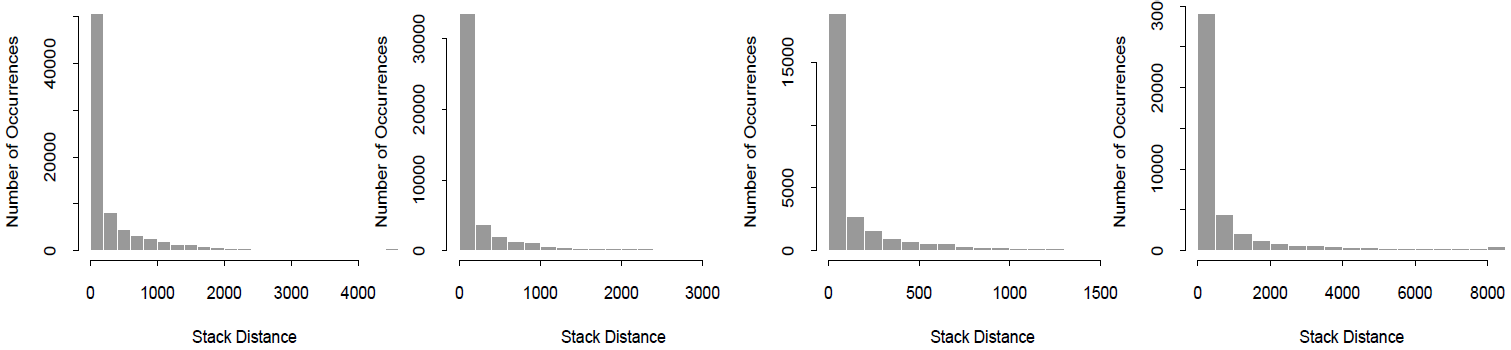
検討対象とする4種類のトレースについて分布を推定するため、Figure 5 にヒストグラムを示す。この図から、ほとんどのスタック距離が \(1\) に近い値に集中していること (すなわちトレースが良好な時間的局所性を示していること) が確認できる一方で、分布には長い裾が存在することがわかる。このデータをモデル化するため、我々は複数種類の長裾分布を検討した。特に、パレート分布 [8] は候補から除外した。その理由は、確かに裾が長いものの、その形状がべき乗則に従っていないように見えるためである。分析の結果、データは対数正規分布 (lognormal distribution) によって最もよく説明されることが判明した。対数正規分布に従うデータは、その対数が正規分布に従うという特性を持つ。得られた分布は非常に長い裾を持つものの、厳密な意味でのべき乗則に従う重尾 (heavy-tailed) ではない。
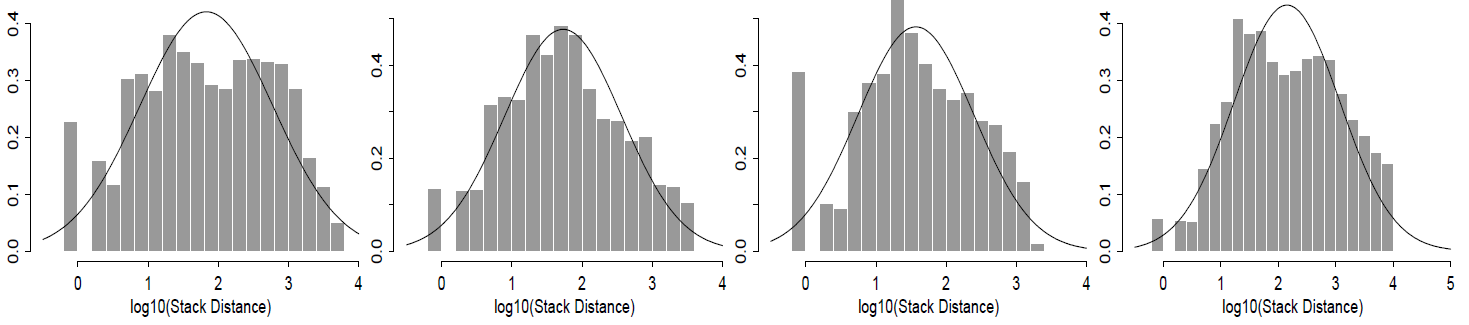
スタック距離をモデル化する際の対数正規分布の適用例を示すため、Figure 6 には実測された分布と適合させた分布をそれぞれ表示している。各プロットでは、スタック距離データの底 \(10\) 対数のヒストグラムを示しており、さらにデータに対する対数正規分布の適合形状も併記している。データセットは一見すると正規分布からある程度乖離しているように見えるかもしれないが、実際にはこの差異は対数変換処理によって強調されたものである。実際、データへの適合度は非常に良好であり、以下に示す通りである。
Figure 6 に示した適合分布を生成するために用いたパラメータ値は Table 3 に記載されている。\(\hat{\mu}\) 列と \(\hat{\sigma}\) 列にはそれぞれ、データセットの底 \(10\) 対数の平均値と標準偏差が示されている。表から明らかなように、本研究で分析対象としたトレース群において、\(\hat{\sigma}\) の値はわずかに変化する程度である。データセット間の差異のほとんどは \(\hat{\mu}\) パラメータに起因している。
| BU | NCSA | SDSC | EPA | |
|---|---|---|---|---|
| \(\hat{\mu}\) | 1.829 | 1.730 | 1.568 | 2.150 |
| \(\hat{\sigma}\) | 0.947 | 0.836 | 0.827 | 0.921 |
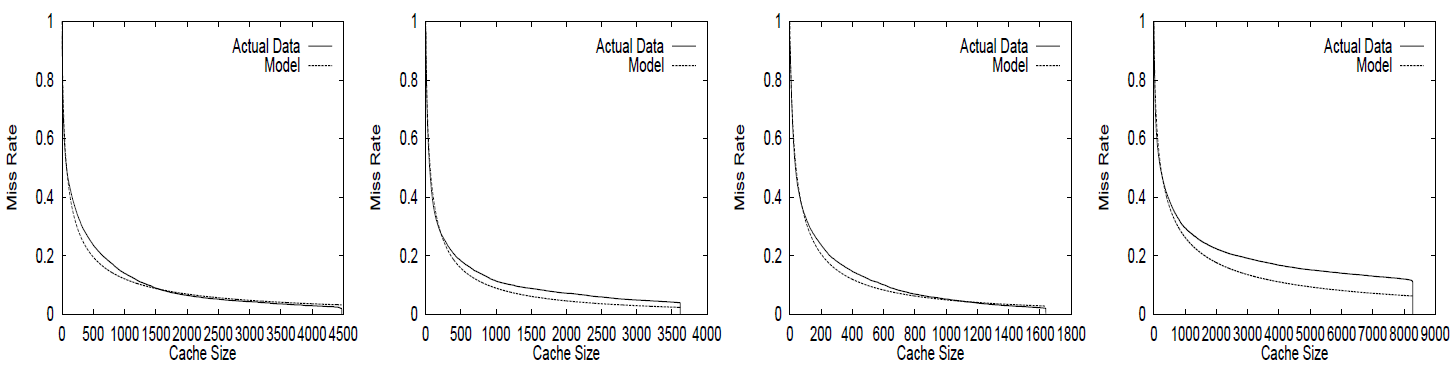
有限キャッシュにおける実際のミス率を対数正規分布がどの程度予測できるかを Figure 7 に示す。前述の通り、\(P[D\gt C]\) をプロットしているが、これはミス率と等価な指標である。各プロットでは、対数正規スタック距離モデルによる予測ミス率と、データから得られた実際のミス率を比較している。いずれのケースにおいても、モデルとデータの一致度は良好である。ただし、EPA トレースに関しては局所性が非常に低いため、この限りではない。
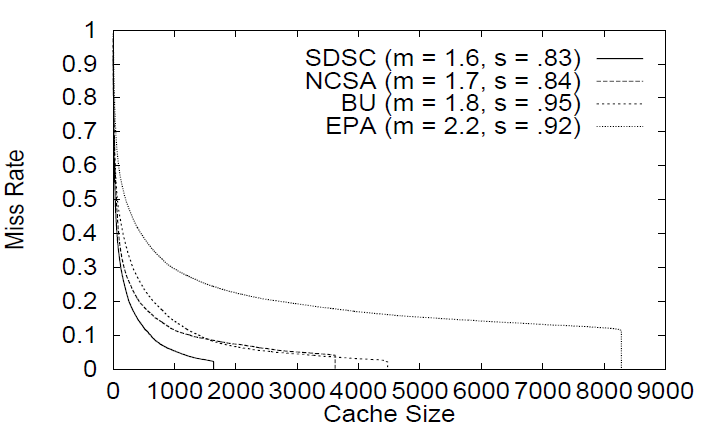
適合パラメータの観点からトレースを比較した結果を Figure 8 に示す。この図は、時間的局所性 (ミス率で測定) が各トレース間でどのように変化するか、およびそれに対応する局所性を捉えるパラメータ値を示している。図から明らかなように、トレースの時間的局所性が低下するにつれて、対数正規分布の平均値は約 1.6 から 2.2 へと上昇し、対数正規分布の標準偏差も緩やかに増加する傾向が見られる (0.83 から 0.95 へと変化)。
 5 空間的局所性の特徴付け
5 空間的局所性の特徴付け
トレース中に観察される時間的局所性を特徴付けた後、ここでは空間的局所性に関するモデルを提示する。これまでの研究により、スタック距離ストリームの相関構造が空間的局所性のモデリングに有効であることが示されている [22]。しかしながら、参照列の相関構造をモデル化する従来の試みでは、有限一次マルコフ連鎖のような短期依存性のみを考慮したモデルが用いられてきた。[24] で指摘されているように、このような短期依存性モデルでは、位相変化挙動を含む参照列の長期的構造を捉えることができない。
スタック距離の自己相似性の測定: スタック距離列における長期的依存性を捉えるため、我々は自己相似性の統計量を用いる。時系列 \(T_t\) が \(H\)-自己相似であるとは、任意の正の伸縮因子 \(c\) に対して、時間スケールを \(ct\) に拡大した再スケーリング過程 \(c^{-H}Y_{ct}\) が、元の過程 \(Y_t\) と分布的に等しくなることを意味する。すなわち: \[ \begin{equation} Y_t =_d c^{-H}Y_{ct} \quad \text{ for all }c,t \gt 0 \label{eq3} \end{equation} \] これは、時系列 \(Y_t\) がフラクタル的な性質を持つことを示している: 詳細があらゆるスケールで存在する。したがって、フラクタル次元に関連する単一パラメータ \(H\) のみを用いることで、幅広いスケール範囲にわたる変動を捉えることが可能となる。
式 \(\ref{eq3}\) はブラウン運動のような運動過程 (この場合 \(H=0.5\)) に適用される。我々のスタック距離トレースのような定常過程に対しては、同等の定義が用いられ、これは定常過程をその定常過程の連続和から構成される対応する運動過程と関連付けるものである。
定義: 連続時間パラメータtを持つ定常過程 \(\{X_t\}\) を考える。このとき、\(X_t\) が \(H\)-自己相似的であるとは、任意の正の集約係数 \(m\) に対して、\(X_t\) を \(m\) 回集約して得られる系列が、分布の意味で \(X_t\) と等しくなることを意味する。すなわち: \[ \begin{equation} X_t =_d m^{-H} \sum_{i=(t-1)m+1}^{tm} X_i \quad \text{ for all } m \in N, t \gt 0 \label{eq4} \end{equation} \]
式 \(\ref{eq4}\) が示すように、すべてのスケールにわたって存在する相関関係により、定常自己相似過程は長距離依存性 (long-range dependency) という特性も有する。長距離依存性を示す時系列データには、通常「バースト」(平均値から大きく乖離した値) があらゆる時間スケールで発生する。つまり、時系列をどのスケールで観察しても、バースト的なパターンが観測可能である。この特性は、長時間スケールでは滑らかな挙動を示す短期依存性モデル (マルコフ過程やポアソン過程など) とは対照的である。
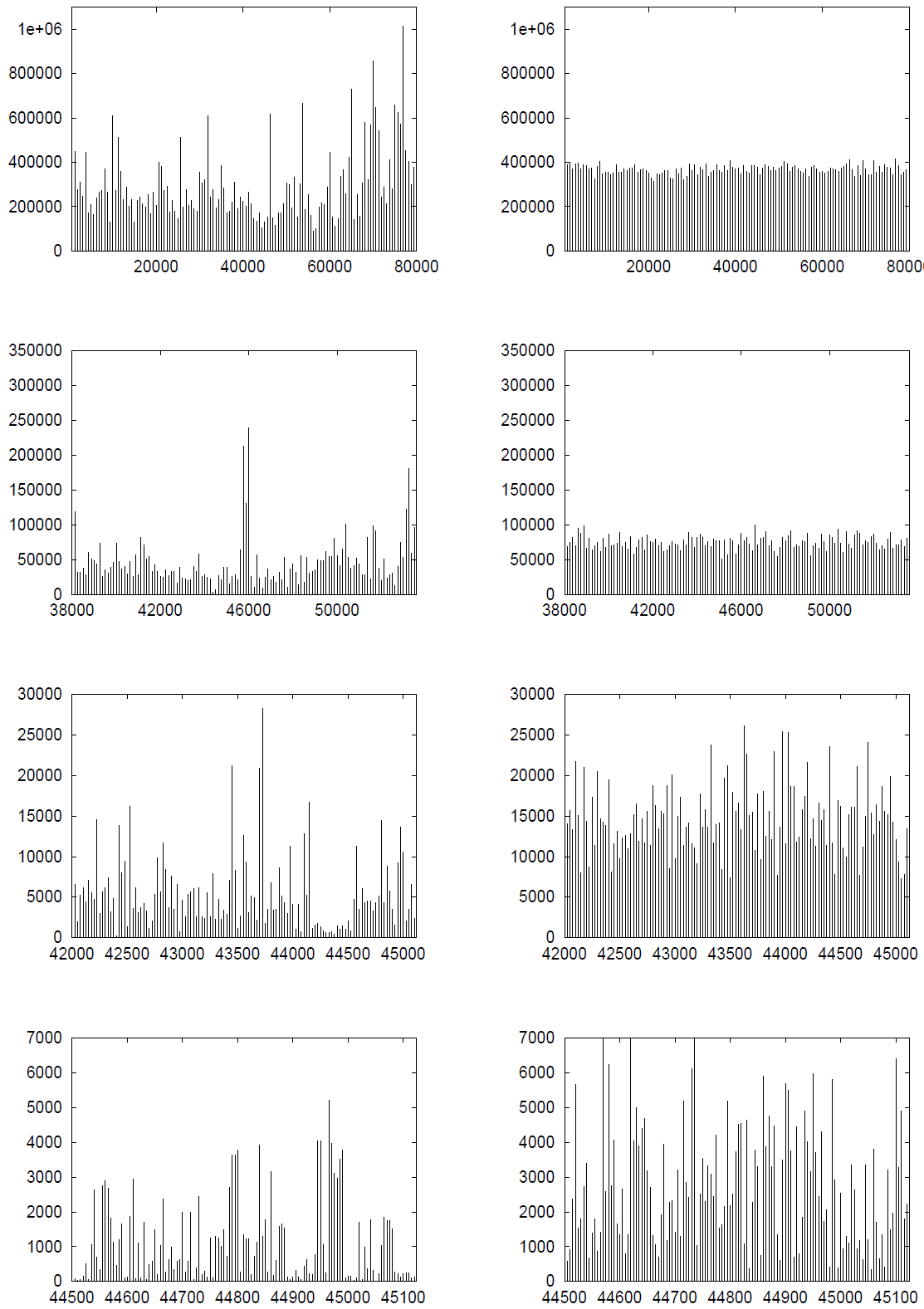
すべての時間スケールにわたってバースト現象が生じるという特性は、スタック距離系列において顕著に現れる。この特性は、従来短期依存性モデルのみでは十分に捉えられないものであった。この効果の具体例を Figure 9 に示す。図では、BU スタック距離の時系列トレースと、まず BU データセットをランダムに並べ替えてからスタック距離を計算して得られた時系列トレースを比較している。両トレースとも同一のファイル参照セットから構成されている点に注意されたい。ただし、並べ替えたデータセットの場合、空間的局所性が破壊されている点が異なる。
図は、詳細度の異なる 2 種類のスタック距離トレースを示している。下部のグラフでは、各データポイントは元のトレースから非重複ブロック単位で連続する 6 個のポイントを加算して算出されている。上から順に、次の系列は下位の系列から 5 個のポイントを加算して形成され、この操作が繰り返される。最上位レベルでは、各データポイントは元のスタック距離系列から 625 個のデータポイントを合計したものとなる。各プロットでは同等の詳細度を示すために 128 ポイントのみを表示しており、最上位レベルではこれが全データ範囲に相当し、下位レベルではプロット範囲が任意に選択されている。このようなデータの加算処理では、短距離依存性は平均化される。もし系列が長距離依存性を持つ場合でも、バースト現象は依然として残る。これは、右側のスクランブル処理を施したトレースと左側の元のトレースを比較することで確認できる。元のトレースに存在するバースト現象は、元のデータセットにおける極めて長距離にわたる相関関係の存在を示しており、これはファイル参照動作の相変化などによって生じる、非常に長期間にわたるスタック距離の大幅な変動に対応するものである。
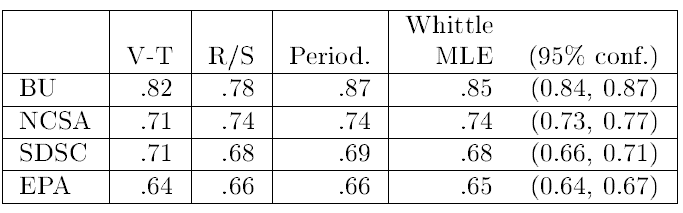
時系列における自己相似性の程度は、パラメータ \(H\) によって定量化される。このパラメータは \(0.5\) から \(1\) の範囲の値を取る。\(H=0.5\) の場合、その時系列には長期的依存性が存在せず、ガウスノイズ (その運動過程はブラウン運動) と同様の振る舞いを示す。\(H\to 1\) に近づくにつれ、集約レベルが高くなるほど時系列のバースト性がより顕著に現れる。本研究では、我々の時系列データに対する \(H\) パラメータを推定するために 4 つの手法を採用した。そのうち 3 手法 ― 分散-時間プロット、\(R/S\) プロット、および周期スペクトル ― はグラフィカルな手法である。これらの手法は、データに関する仮定 (定常性など) の妥当性を評価するのに有用であり、単一のH推定値を提供する。これら 3 つのグラフィカル手法はいずれも X-Y プロットを生成し、プロットにおける直線性は基礎となる時系列に長期的依存性が存在することを示す。各ケースにおける直線の傾きを用いることで、\(H\) 値を推定することが可能である。4 つ目の手法は、ウィトル推定量 (Whittle estimator) と呼ばれる \(H\) の最尤推定法であり、これに加えて信頼区間も算出できる。これらの手法についてより詳細な議論を知りたい読者は、文献 [3, 16] を参照されたい。
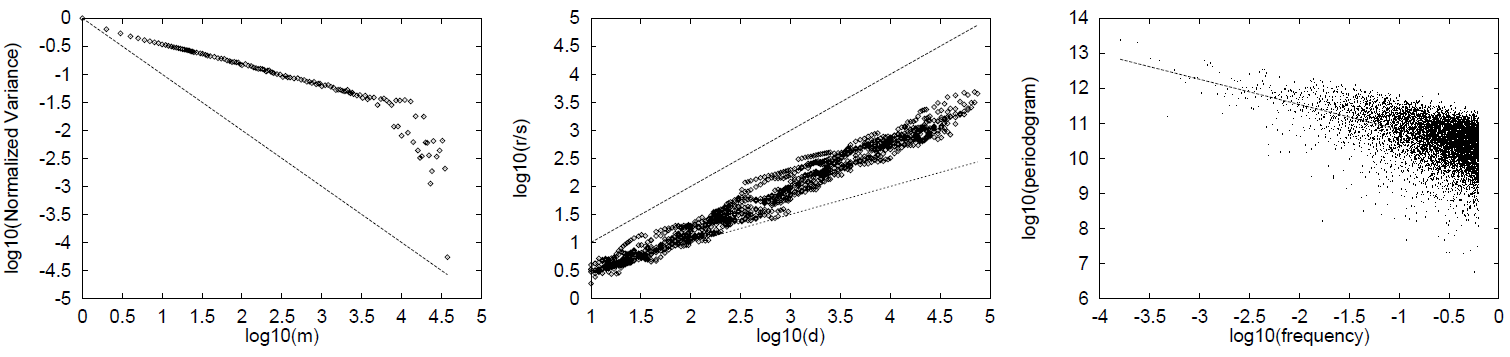
BU トレースに対するグラフィカル推定量のプロットを Figure 10 に示す。左側は分散-時間推定量のプロットであり、大部分の範囲において強い線形性を示しており、直線の傾きから \(\hat{H}=0.82\) という推定値が得られる (参考として、\(H=1/2\) に対応する直線もプロットしている)。中央には \(R/S\) 統計量のプロットを示している。ここでも、明らかな線形性が長距離依存性の存在を示唆しており、直線の傾きから \(\hat{H}=0.78\) という推定値が得られる。このプロットにおいても、参考として \(H=1/2\) および \(H=1\) に対応する直線をプロットしている。右側は周期スペクトル推定量のプロットである。このプロットに見られる顕著な散布は典型的な特徴であるが、背後には明確な線形トレンドが存在しており、点群に対する最小二乗法による近似から \(\hat{H}=0.87\) という値が導かれる。このように、これらの各プロットはいずれも自己相似性の存在を示唆している。他の 3 つのスタック距離トレースに対するグラフィカル結果については図示していないが、これらも同様の線形性を示している。
グラフィカルな推定手法に加え、ウィトルの最尤推定量 (WML推定量) を用いて、我々のデータセットにおける \(H\) 値の推定も行った。いずれのケースにおいても、推定値間には合理的な一致が見られ、\(H\) 値は \(1/2\) を大幅に上回る値となった。4 つのデータセットに対する推定結果を Table 4 に示す。\(H\) 値の範囲は、BU データセットで約 0.85 から、EPAデータセットで約 0.65 までとなっている。
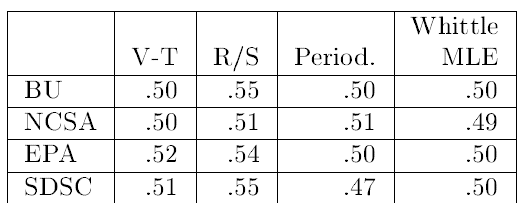
元のトレースデータをスタック距離列に変換する処理自体がデータに依存性を生じさせている可能性について検討した。この疑問に答えるため、各データセットをランダムに再配列し、それに対応する新たなスタック距離系列を計算した上で、得られた系列のH値を推定した。その結果を Table 5 に示す。これらの推定値はいずれも \(1/2\) に極めて近く、系列に長期的依存性が存在しないことを示している。この結果から、これらの時系列データに見られる長期的依存性は、元の参照トレースにおける記号パターン間の実際の相関関係を反映していると結論づけられる。
フラクタル・キャッシュミスパターンとの関連性: Figure 9 を別の観点から解釈すると、上から下に向かって「データの詳細度を上げていく」過程と見ることができる。図の左側のプロットがあらゆるスケールでほぼ同程度のバースト性を示しているという事実は、スタック距離トレースがフラクタル的な性質を持つことの証拠である。
実際、フラクタル幾何学は過去において、コンピュータシステムにおける参照局所性の特徴として指摘されてきた。特に Voldman ら [26] は、科学的計算、データベース処理、汎用処理という 3 種類の異なるワークロードにおけるキャッシュメモリシステムのミスデータを分析している。著者らは、これらのキャッシュミス系列のいずれもがフラクタルパターンを示すことを明らかにした。すなわち、個々のミスイベントは時間的にクラスタを形成し、これらのクラスタがさらにクラスタを形成するといった構造が見られる。彼らの研究結果の一つとして、参照番号を座標としてキャッシュミスイベントを数直線上にプロットした場合、その結果得られるパターンの次元は 0 から 1 の間のフラクタルパターンとなるというものがある。
我々の研究成果を Voldman らの研究結果と関連付けるため、まずスタック距離トレースの自己相似性に着目する。この性質は、スタック距離トレース自体がフラクタル構造を持つことを意味する。統計的に自己相似な時系列 \(X_t\) (Figure 9 左側の例のような系列) は、そのフラクタル次元が Hausdorff 次元 \(\dim_H\) または箱数え次元 \(\dim_B\) のいずれかの意味において [11] \[ \dim(X_t) = 2 - H \] というほぼ確実な値を取る。したがって、このような時系列のフラクタル次元は、ガウスノイズの場合 (\(H=1/2\)) には \(3/2\) となり、系列内に存在する相関が増大するにつれて (\(H\to 1\)) 1 へと減少する。これは、依存関係がより強い系列ほど「予測可能性が高く」、空間をより完全に埋め尽くさないという直感的な理解と一致する。
我々の研究と [26] の研究の関連性は、スタック距離が自己相似である場合、キャッシュミスにフラクタル特性が現れると予想できる点にある。その理由は次の通りである。キャッシュミスパターンは、スタック距離トレースと X 軸に平行なある固定キャッシュサイズに対応する直線との交点として可視化できる。\(1 \lt \dim_H(X) \lt 2\) を満たすフラクタル \(X\) と、\(\dim_H(L)=1\) を満たすある直線 \(L\) との交点は、ほぼ確実に新たなフラクタル \(X'\) を生成し、そのフラクタル次元は \(\dim_H(X')=dim_H(X)-1\) となる [17]。つまり、我々のトレースデータのようなスタック距離フラクタルから導出されるキャッシュミスフラクタルの次元は、0 から 1 の間にあるはずである。実際に我々はこの効果を観測しており、我々のトレースデータにおけるキャッシュミスが Voldman らによって以前に観察されたパターンと一致するフラクタル特性を示すことを確認している。
以上のことから、我々の研究成果はキャッシュミスパターンのフラクタル的性質に関する新たな視点を提供するものであると言える。ただし、本研究ではこれらの結果を WWW 参照パターンのケースに拡張し、さらに次節で述べるように、フラクタル特性を利用して合成トレースを生成する方法についても示している。
合成 Web 参照トレースの生成: 現実的な Web 参照トレースに存在する時間的局所性と空間的局所性を可能な限り忠実に再現するためには、合成トレースの生成においてこれらの特性を厳密に模倣することが重要である。本論文で提案する生成プロセスは以下の通りである:
時間的局所性を反映するパラメータ \(\mu\) と \(\sigma\)、および空間的局所性を反映するパラメータ \(H\) を選択する。これらのパラメータは、模倣対象とする実際のトレースの経験的測定値に基づいて決定するか、本論文で報告するトレースデータから得られる値の範囲から選択することができる。
\(\mu\) と \(\sigma\) によって決定される周辺分布と、\(H\) によって決定される長距離依存性を持つスタック距離トレースを生成する。
生成したスタック距離トレースを反転処理し、ファイル名のシーケンスを形成する。
一見すると、ステップ 2 の処理は困難に思えるかもしれない。しかし幸いなことに、近年の研究により、トレース生成における周辺分布と長距離依存性はそれぞれ独立した問題として扱えることが示されている [15]。この研究によれば、\(H=H_X\) を満たす長距離依存性系列 \(X_t\) と、その周辺累積確率関数 \(F_X(x)\) が与えられた場合、任意の周辺累積確率関数 \(F_Y(x)\) を持つ別の長距離依存性系列 \(Y_t\) を生成することが可能である。これは \(X_t\) の各要素を以下のように個別に変換することで実現される: \[ \begin{equation} Y_t = F_Y^{-1}(F_X(X_t)) \label{eq5} \end{equation} \] [15] の著者らは、この変換手法によって \(H\) の値を変更せずに長距離依存性が保持されることを実証している。
したがって、我々のステップ 2 へのアプローチは以下のように構成される。まず第一に、与えられた \(H\) 値を持つ自己相似系列を生成する。これには複数の方法が可能であり、迅速な手法については [20] で詳細に説明されている。次に、式 \(\ref{eq5}\) に示す変換を適用することで、所望の対数正規分布を持つ周辺分布を持つ系列を得る。
我々は現在、Web 参照トレースを生成するための本手法の適用を開始しており、生成されたトレースの特性評価を進行中である。現時点で実施した、時間的局所性特性のみをモデル化した初期実験の結果は有望である。
 6 関連研究
6 関連研究
モデリング手法: Denning と Schwartz [10] は、記憶階層構造における局所性現象を特徴づける基本特性を確立した。[19] において、著者らはスタックアルゴリズムを研究し、要求ページ方式メモリシステムの動作解析手法としてスタック距離概念を導入した。さらに、メモリ管理方式の性能評価におけるスタック距離列の重要性についても論じている。その後、Spirn [24] はプログラム動作を表現する手法として距離列モデルの利用を提案した。距離列は参照列と同等の情報量を持ちながら、数学的モデルによる扱いが容易であるという特徴を有する。距離列モデルとLRUスタックモデルは等価であり、距離列の情報から各時点における LRU スタックを特定することが可能である。しかしながら、提案された距離列モデルは参照間の長距離依存関係を捉えることができない。著者が指摘するように、このモデルは実際のプログラムにおいてクラスタ状に発生しやすいページフォルト現象を正確に表現できない。局所性の変化がページ単位で漸次的に起こる場合、参照の局所性をモデル化することは比較的容易である。しかし実際のプログラムでは、新たな処理フェーズの実行によって実行時の局所性集合が完全に破壊される場合が多い。通常、このような局所性の急激な変化は距離列モデルにおいて大きな距離値を生成する。マルコフ距離列モデルは、直近に生成された距離値に基づいてバースト現象を予測することが可能である。したがって、[24] の研究では、マルコフモデルが実際のプログラムに見られる何らかの長距離依存性を伴う動作特性を捉えられないことが主張されている。著者はさらに、距離確率に基づくこれらのモデルが、長距離効果を模倣する能力に欠けているため、プログラム動作のシミュレーション研究には適していないと指摘している。
フラクタルの応用: セクション 5 で述べたように、コンピュータシステムの挙動解析にフラクタル幾何学と自己相似性を適用する手法は、Voldman らの研究 [26] によって先駆的に確立された。著者らは 3 種類のソフトウェア環境におけるメモリ参照トレースを分析し、各環境におけるインターミス間隔の分布がべき乗則に従うことを発見した。この結果は、システムがフラクタル的な挙動を示していることを強く示唆している。キャッシュミスは時間軸上でクラスタを形成し、これらのクラスタは統計的に自己相似性を示す。本研究の分析結果から、特定のキャッシュミス分布のフラクタル次元は、基礎となるソフトウェアの複雑性を測る指標となり得るという仮説が導かれた。
[26] の研究を発展させた [25] 論文では、プロセッサがメモリにアクセスする際に生成されるパターンを、フラクタル次元を持つランダムウォークとしてモデル化している。著者は、無限サイズのキャッシュを想定した場合、プログラムが遭遇するキャッシュミスの総数はフラクタル次元の双曲関数で表されると提案している。さらに同論文では、キャッシュミスを近似的に解析するためのモデルも提示されている。このモデルは 2 つの明確な段階に分かれており、一方は「強制モード」と呼ばれ、システムのコールドスタート過程を表現する。もう一方の「フラクタルモード」段階は、キャッシュの安定動作状態をモデル化したものである。ただし、このモデルはトレースプロットからパラメータを取得・調整するという経験的な手法を必要とするため、実用面では課題が残る。また、提案モデルはコンテキストスイッチが頻繁に発生するマルチプログラミング環境を適切に表現できないという限界も存在する。
本論文では、[26, 25, 24] の先行研究を拡張し、大規模分散システムの文脈においてこれらの知見を適用するとともに、Web サーバに流入する参照ストリームの局所性特性を完全に記述するための新たなパラメータを追加している。
Web 参照の局所性の活用: 大規模分散情報システムにおけるキャッシュ、複製、配信、事前取得プロトコルに関する従来の研究では、本論文で検討した各種参照局所性特性が認識され、実際に活用されてきた。本節の残りの部分では、これらのプロトコルについて簡潔に概説する。紙面の制約上、ここでは Web 関連の研究に限定して述べる。
Glassman [12] は、Web 上でのキャッシュ技術に関する初期の試みの一つとして、「衛星中継器」(プロキシキャッシュ) をツリー構造の階層的に配置する方式を提案している。この方式では、下位の中継器で発生したキャッシュミスが上位の中継器へと伝播し、要求されたオブジェクトが発見されるまで検索が行われる。このキャッシュシステムの単一中継器における性能評価では、比較的小規模なキャッシュサイズであっても、約 33% という「比較的安定した」ヒット率を維持可能であることが示された。Zipf 分布に基づくモデルを用いた場合、無限サイズのキャッシュを想定すると、達成可能な最大ヒット率は 40% と推定されている。Web アクセスパターンを特徴付ける初期の研究としては、Recker と Pitkow [21] の研究が挙げられる。同研究では、人間の記憶に関する心理学的研究から借用した 2 つの指標 ― 過去のアクセス頻度と最新アクセス頻度 ― に基づいて、Web 情報アクセスのモデルが提案されている。
Web 向けクライアントベースキャッシュに関する最初の包括的研究は、我々の Oceans グループによって実施された6。この研究 [6] では、Mosaic [9] に計測機能を組み込むことで取得した 5,700 件のクライアントトレース (約 60 万件の URL リクエストを含む独自のデータセット) を用いて、セッションキャッシュ、ホストキャッシュ、LAN プロキシキャッシュの有効性を検証した。その結果、LAN プロキシキャッシュは応答時間を最大 50% 短縮する効果があるものの、最終的には同一サイトのクライアント間で遠隔文書が共有される度合いが低いという制約を受けることが明らかになった。本研究のこの知見は Glassman の予測 [12] と一致しており、Abrams ら [1] による一般的なプロキシキャッシュに関する研究によってもさらに裏付けられている。
[18] において、Markatos はメインメモリ Web キャッシュの利用による性能向上の可能性について考察している。彼は、文書の人気度や小規模文書に対するユーザーの選好傾向に敏感なキャッシュ管理手法 [9] を採用すれば、少量のメインメモリであっても性能面で顕著な改善が得られることを実証している。
Web アクセスパターンに顕著に現れる参照の空間的局所性を活用する手法については、当研究グループの Oceans チームが最近実施した2つのプリフェッチング研究で調査されている。[7] において、Bestavros と Cunha は、クライアントの過去のアクセスパターンから構築したマルコフモデルに基づいて、クライアントが Web 文書を事前に取得できるようにするプロトコルを提案している。[5] では、Bestavros が、サーバーのアクセスログを分析して構築したマルコフモデルに基づき、サーバー側で生成したヒントを契機としてプリフェッチを開始させるプロトコルを提案している。
 7 結論
7 結論
本論文では、World Wide Web 上の 4 つのサーバーに送信される参照トレースデータに存在する局所性を測定し、本データセットの局所性特性を捉える統計モデルを提示した。これらのモデルは、異なる参照ストリームの比較、キャッシュ性能の予測、および現実的な特性を持つ合成参照ストリームの生成に応用可能である。
まず第一に、文書の人気度のみに基づく単純な手法では、トレースデータに存在する時間的局所性と空間的局所性のいずれも適切に捉えられないことを実証した。次に、参照トレースの時間的局所性特性を測定した結果、スタック距離分布をモデル化する際には対数正規分布が妥当なモデルであることを明らかにした。最後に、空間的局所性をモデル化するため、参照パターンの長期的挙動を捉えるには長距離依存性を考慮したモデルが不可欠であることを理論的に論じた。
現在進行中の研究では、これらの局所性モデルを拡張し、文書サイズを明示的にモデル化する手法を開発している。さらに、本研究がサーバーから取得したトレースデータに基づいている一方で、クライアント側で取得された参照トレースの局所性特性にも関心を抱いており、これらの特性がクライアント近傍でのストリーム取得時とサーバー近傍での取得時でどのように変化するかを調査している。
Acknowledgements: The authors thank John Dilley and PDIS anonymous referees for comments that improved the content and presentation of this paper.
 References
References
- Marc Abrams, Charles R. Standridge, Ghaleb Abdulla, Stephen Williams, and Edward A. Fox. Caching proxies: Limitations and potentials. In Proceedings of the Fourth International Conference on the WWW, Boston, MA, December 1995.
- S. Acharya, R. Alonso, M. Franklin, and S. Zdonik. Broadcast disks: Data management for asymmetric communications environments. In Proceedings of ACM SIGMOD, San Jose, CA, May 1995.
- Jan Beran. Statistics for Long-Memory Processes. Monographs on Statistics and Applied Probability. Chapman and Hall, New York, NY, 1994.
- Azer Bestavros. Demand-based document dissemination to reduce traffic and balance load in distributed information systems. In Proceedings of SPDP: The 7th IEEE Symposium on Parallel and Distributed Processing, San Antonio, Texas, October 1995.
- Azer Bestavros. Using speculation to reduce server load and service time on the www. In Proceedings of CIKM: The 4th ACM International Conference on Information and Knowledge Management, Baltimore, Maryland, November 1995.
- Azer Bestavros, Robert Carter, Mark Crovella, Carlos Cunha, Abdelsalam Heddaya, and Sulaiman Mirdad. Application level document caching in the internet. In IEEE SDNE: The Second International Workshop on Services in Distributed and Networked Environments, Whistler, British Columbia, June 1995.
- Azer Bestavros and Carlos Cunha. A prefetching protocol using client speculation for the www. Technical Report TR-95-011, Boston University CS Dept., Boston, MA 02215, April 1995.
- Mark E. Crovella and Azer Bestavros. Self-similarity in World Wide Web traffic: Evidence and possible causes. In Proceedings of the ACM SIGMETRICS, May 1996.
- Carlos A. Cunha, Azer Bestavros, and Mark E. Crovella. Characteristics of www client-based traces. Technical Report TR-95-010, Boston University, Department of Computer Science, April 1995.
- P. Denning and S. Schwartz. Properties of the working set model. Communications of the ACM, 15(3):191–198, 1972.
- Kenneth Falconer. Fractal Geometry. John Wiley & Sons Ltd, 1990.
- Steven Glassman. A caching relay for the world wide web. In Proceedings of the First International Conference on the WWW, 1994.
- James Gwertzman and Margo Seltzer. The case for geographical push caching. In Proceedings of HotOS: The Fifth IEEE Workshop on Hot Topics in Operating Systems, Washington, May 1995.
- The Internet Town Hall. The internet traffic archive. http://www.town.hall.org/Archives/pub/ITA.
- Changcheng Huang, Michael Devetsikiotis, Ioannis Lambadaris, and A. Roger Kaye. Modeling and simulation of self-similar variable bit rate compressed video: A unified approach. In Proceedings of ACM SIGCOMM 95, pages 114–125, 1995.
- W.E. Leland, M.S. Taqqu, W. Willinger, and D.V. Wilson. On the self-similar nature of Ethernet traffic (extended version). IEEE/ACM Transactions on Networking, 2:1–15, 1994.
- Benoit B. Mandelbrot. The Fractal Geometry of Nature. W. H. Freedman and Co., New York, 1983.
- Evangelos Markatos. Main memory caching of web documents. In Proceedings of the Fifth International Conference on the WWW, Paris, France, 1996.
- R. Mattson, J. Gecsei, D. Slutz, and I. Traiger. Evaluation techniques and storage hierarchies. IBM Systems Journal, 9(2):78–117, 1970.
- Vern Paxson. Fast approximation of self-similar network traffic. Technical Report LBL-36750, Lawrence Berkeley Lab, Berkeley, CA, 1995.
- Mimi M. Recker and James E. Pitkow. Predicting document access in large multimedia repositories. Technical Report Technical Report VU/GIT-95-02, Georgia Tech—Graphics, Visualization, and Usability Center, August 1995.
- G. Shedlar and C. Tung. Locality in page reference strings. SIAM Journal of Computing, 1(3):218–241, Sept. 1972.
- Alan Jay Smith. Cache memories. Computing Surveys, 14(3):473–530, September 1982.
- Jeffrey Spirn. Distance string models for program behavior. IEEE Computer, 9(11):14–20, November 1976.
- Dominique Thiebaut. On the fractal dimension of computer programs and its application to the prediction of the cache miss ratio. IEEE Transactions on Computers, 38(7):1012–1026, July 1989.
- Jean Voldman, Benoit Mandelbrot, Lee W. Hoevel, Joshua Knight, and Philip L. Rosenfeld. Fractal nature of software-cache interaction. IBM Journal of Research and Development, 27(2):164–170, 1983.
- G. K. Zipf. Human Behavior and the Principle of Least Effort. Addison-Wesley, Cambridge, MA, 1949.
翻訳抄
World Wide Web サーバーに到着するリクエストストリームにおける参照の局所性を、時間的・空間的側面から定量的に特徴づけた 1996 年の論文。スタック距離の対数正規分布と自己相似性に基づくモデルにより、従来の人気度ベースのモデルでは捉えられなかった局所性を表現できることを実証した。
- ALMEIDA, Virgilio, BESTAVROS, Azer, CROVELLA, Mark, and DE OLIVEIRA, Adriana. Characterizing Reference Locality in the WWW. In: Proceedings of PDIS'96: The IEEE Conference on Parallel and Distributed Information Systems. Miami Beach, FL, December 1996.
