分位数

概要

分位数 (quantile) またはクォンタイルはデータや確率の分布を一定の割合で区切るための値を指す。例えばデータを昇順に並べたとき、その累積割合が特定の値 (20%, 50%, 75% など) となる点を示すことで、データのばらつきや中心傾向、偏りなどを把握しやすくするための指標として使用される。

\(q\)-分位数 (\(q\)-quantile) はデータ全体を下から \(q \in [0,1]\) の位置で区切る値であり、累積分布関数において確率が \(q\) となる点である (0.5 分位数は中央値 (median) である)。一般的な分位数には四分位数や百分位数がある。また \(q\) をパーセントで表した表記をパーセンタイル (percentile) と呼ぶ。

\(n\) 個の数値の集合から \(k\) 番目に小さい数値を探すアルゴリズムを選択アルゴリズムと呼ぶ。このとき \(k=qn\) に位置する数値は分位数 \(q\) に相当する分位点である。したがって分位数 \(q\) の分位点は選択アルゴリズムによって見つけることができる。

サイズ \(N\) の順序集合から \(p\) パスで正確な分位点を取得するには \(\Omega(N^{1/p})\) の空間が必要となることが証明されている [3]。したがってストリーミング処理において \(p=1\) パスで正確な分位点を求めることは現実的ではなく、このため大規模データセットに対しては近似分位数を求める研究がなされている。

Table of Contents

1. 概要
2. Floyd-Rivest アルゴリズム
3. \(q\)-digest
4. \(t\)-ダイジェスト
5. 参考文献

Floyd-Rivest アルゴリズム

Floyd-Rivest アルゴリズムは \(n\) 個の数値の集合から \(k\) 番目に小さい要素を \(O(n)\) で見つけるための選択アルゴリズムである。QuickSelect アルゴリズムに似ているが計算量はより少ない。これは Quick ソートのようにパーティションに分けて分割統治するが、\(O(n \log n)\) となる完全なソートと違って目的のランクに存在する数値を見つける動作のみを行う。

1. 集合のサイズが十分に小さい場合 (元の論文著者は 600 以下としている)、QuickSelect アルゴリズムにフォールバックして \(k\) 番目の要素を得る。

\(q\)-digest

\(q\)-digest [2, 1] はデータの頻度分布の要約表現である。ヒストグラムのように頻度をデータごとに配列で表す代わりに、頻度の大きさに応じた範囲で合算統合し木構造のノードとすることで全体のサイズを圧縮する。元は非力なセンサーネットワークを介して計測値の頻度を交換するための方法として提案された。

あるデータソースから \([1,\sigma]\) 範囲のデータを合計 \(n\) 個取得したと仮定する。この正確な表現はデータごとの頻度の配列 \((f_1,f_2,\ldots,f_\sigma)\) である。ここで \(f_i\) はデータ \(i\) を観測した回数を表す。したがって \(\sum_{i=1}^\sigma f_i = n\) である。

\(q\)-digest はまず各頻度を葉とする二分木を構築する。次に、以下の 2 つの制約を再帰的に適用し、隣接する頻度の小さいノード (バケット) を上位ノードに統合する。ここで \(k\) は圧縮係数 (compression factor) と呼ぶ。

1. 葉ノードを除き、ノード \(v\) の頻度は \(\lfloor n/k \rfloor\) 以下でなければならない。

2. ルートノードを除き、ノード \(v\) とその兄弟 \(v_s\)、親 \(v_p\) の頻度の合計は \(\lfloor n/k \rfloor\) より大きくなければならない。

この操作により、頻度の高いデータは高解像度で、頻度の低いデータは低解像度で不可逆圧縮される。

Fig 1 は \(q\)-digest による頻度分布の圧縮過程を示している。初期状態の配列構造では少なくとも 7 つの頻度値を保存する必要があるが、q-digest で圧縮した後では 5 個の頻度値を保存すれば良い。

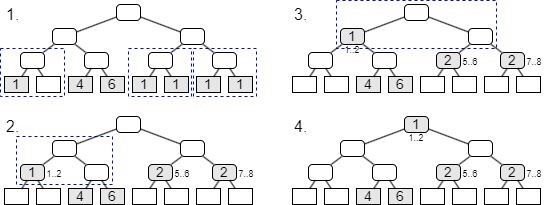
同一の \(\sigma\) と \(k\) を持つ複数の d-ダイジェストを 1 つの q-ダイジェストにマージすることができる。これはツリーの各ノードを合算統合したあとに Fig 1 のような圧縮操作を行うことで可能である。これにより複数のデータソースから個別に集計した頻度をマージするような使い方ができるため map-reduce のような並列化手法に適用できる。。

\(q\)-digest に対する分位点クエリーは、分位数を \(q\) としたとき、\(n\) 個のデータのうち昇順で \(qn\) 番目のデータが \(q\)-digest のどのノードに属しているかを調べる。これは範囲の最小値を持つノードから順にトラバースすることで見つけることができる。該当するノードのデータ範囲の最大値を分位点として採用する。同様に逆分位数 (あるデータ \(x\) に対応するランクや分位点) クエリーや範囲クエリーも可能である。

\(t\)-ダイジェスト

\(t\)-ダイジェスト (\(t\)-digest) [4, 1] は大規模なデータセットから分位数の近似値を高精度かつメモリ効率的に算出するためのアルゴリズムである。入力データをクラスタ化 (分割) し、それぞれの重心を算出することで、データ全体の分布を効率的に要約する。分布の両端 (極値) と中央でクラスタのサイズ (重み) を変えて分位数を高い精度で近似する。このサイズ制限はスケール関数と呼ばれる単調増加の関数で定義される。複数の t-digest を容易に統合できるため、map-reduce のような分散処理フレームワークに適用が可能である。

参考文献

1. Dzejla Medjedovic, Emin Tahirovic, Ines Dedovic. 大規模データセットのためのアルゴリズムとデータ構造. マイナビ出版 (2024)
2. Nisheeth Shrivastava, Chiranjeeb Buragohain, Divyakant Agrawal, Subhash Suri. Medians and beyond: new aggregation techniques for sensor networks. In: Proceedings of the 2nd international conference on Embedded networked sensor systems. 2004. p. 239-249.
3. Munro, J.I., & Paterson, M.S. 1980. Selection and sorting with limited storage. Theoretical Computer Science, 12(3), 315 – 323.
4. DUNNING, Ted; ERTL, Otmar. Computing extremely accurate quantiles using \(t\)-digests. arXiv preprint arXiv:1902.04023, 2019.