非復元ランダムサンプリングにおける公平性
Abstract
利益配分や機会の割り当て手段において公平性 (fairness) を保証する設計は必須の要件である。これは分散システムでの役割分担や負荷分散でも同様に考慮しなければならない。現実世界の抽選をモデルとしたスキームはランダムな事象を用いて公平性を実装している一方で、重み付きの非復元ランダムサンプリング (weighted random sampling without replacement; WRSwoR) においては既に選択された対象が候補から除外されるという特性によって公平さが欠落している。
この文書では重み付き非復元ランダムサンプリングにおける公平さ欠如を機会損失のモデルで説明し、WRSwoR に公平性をもたらす調整パラメータを算出する方法を示す。
Table of Contents
Introduction
復元サンプリングと非復元サンプリング
ある \(n\) 個の要素からなる母集団 \(G\) から \(m\) 個の標本を選択して部分集合 \(\hat{G}\) を作成する問題について考える。最も簡単な方法は母集団 \(G\) に対して単一のランダムサンプリングを \(m\) 回繰り返すことである (繰り返し乱択)。この方法は壺問題
において選択した要素を再び壺に戻して (状態を復元して) 次の抽選を行う方法と同等であるため復元サンプリング (random sampling with replacement) と呼ばれている。
復元サンプリングでは要素が選択された後も母集団 \(G\) に存在し続けることから、抽出数が \(m\) に到達しない限り同じ要素が何度でも選択される可能性がある。つまり、選択された標本の集合 \(\hat{G}\) には同一の要素が繰り返して出現する可能性があることに注意しなければならない。このような重複選択の問題は、母集団 \(G\) の要素数 \(n\) が非常に大きいケース、例えば国内の全インフルエンザ罹患者から 100 人の症例を抽出するようなケースにおいては発生の確率が非常に低いことから無視されることもある。
しかし現実問題としては物理的な制約を理由に標本集合 \(\hat{G}\) に同一の要素が繰り返し存在することを許容できないケースも多い。21 人の自治会から選挙の立会人を 3 名選ぶとき、3 名という人数が重要であって、重複選択で 1 名が 2 度選択されたとしても都合 2 名で立会人を務めることは (うち 1 名が 2 人分働くと主張したとしても) 一般には許容されない。このようなケースでは抽選で選択された要素が重複していないことを保証することが重要となる。
このような状況では既に選択された要素を母集団 \(G\) から除外するスキームにより重複した選択が発生しないランダムサンプリングを構築することができる。このスキームは状態を復元しないことから非復元ランダムサンプリング (random sampling without replacement) と呼ばれる。非復元サンプリングを \(m\) 回繰り返すことで繰り返し選択の問題を解決することができるが、他方で、ある選択がそれ以降の選択に影響を与えることによって \(m\) 回のサンプリングそれぞれが独立な事象ではないという新たな問題をもたらす。
非復元サンプリングにおける選択の非独立性は、すべての要素が同じ確率で選択されるケースでは問題視されないが、それぞれの要素に選択の優先度となる重みや優先度を設定されている場合に、要素の選択頻度がその重みと一致しないという形で顕在化する。
問題のシミュレーション
重み付き非復元サンプリングではどのような問題が起きるのかを先にシミュレーションで見てみよう。以下のデモは各要素の重みの分布と、重み付き非復元ランダムサンプリングを繰り返し行ったときの実際の選択頻度を比較している。
Inverse (逆数) の重み分布に対して ×1,000 を実行してみれば明らかなように、それぞれの要素の選択頻度の分布 (Actual Win Rate) は重みの分布とはかけ離れた挙動となる。唯一一致する分布は Flat だけだが、これはすべての要素の重みが等価であることから一様ランダムサンプリングと同じ意味である。つまり、この重みと選択頻度の分布が一致しない現象は重み付き非復元ランダムサンプリング固有の特徴と言える。
このシミュレーションでは累積和法 (cumulative sum) のケースに対してのみ、この文書で示している補正を行った Corrected Win Rate の曲線を追加している。
機会損失モデル
重み付き非復元サンプリングにおいてなぜこのような現象が起きるのかを考えてみよう。元となる母集団の重みの総和を \(W=\sum_i w_i\) としたとき 1 回の抽選で要素 \(i\) が選択される確率は \(p_i=w_i/W\) と表すことができる。非復元サンプリングでは、選択された要素がそれ以降の抽選から除外されるため、後の抽選になるほど母集団の重みの総和 \(W\) が小さくなる。つまり、2 回目以降の抽選で選択された要素は本来の選択確率より高い確率で選択されており、その傾向は後の抽選になるほど高くなることが考えられる。
これが重み付きとなるとより重みの大きい要素は早期の抽選で選択されやすい傾向が加わる。したがって、直感的には、より大きな重みを持つ要素は実際の重みよりも低い頻度で、より小さな重みを持つ要素は実際の重みよりも高い頻度で選択される傾向となって現れる。実際に前述のシミュレーションではそのような傾向が見て取れる。
以降はこの現象に関する文献や研究が見つからなかったため作成した自論のモデルです。もし先行研究に心当たりがあればコメントに残しておいてもらえるとありがたいです。
この現象は機会損失を使って説明することができる。機会損失と期待値の理解を助けるためにいくつかの例を見てみよう。
例 1 . 20 人に一人の確率で 10,000 円が当たるスクラッチくじが 550 円で売っていた。あなたはこのスクラッチくじを買うべきだろうか?
スクラッチくじを 1 回引いたときの報酬の期待値は \(\frac{10000}{20}=500\) 円である。これはスクラッチくじに参加すること自体が 1 回あたり 500 円の価値に換算できると考えることもできる (結果がまだ確定していない段階では、という意味に注意)。つまり、このスクラッチくじを 550 円で買うことは 500 円の価値を 550 円で買うことを意味しており、結果的に 50 円の損になる。したがって (娯楽性や話題性を無視し金額上の純粋な損得で考えると) 買うべきではない。
例 2 . あなたは 20 人に一人の確率で 10,000 円が当たるスクラッチくじを所有している。しかし、いざ削ってみると印刷ミスで結果が記載されておらず抽選は無効となってしまった。あなたが受けた損失はいくらだろうか?
このスクラッチくじの抽選に参加すること自体に 500 円の価値があることは例 1 で述べた。したがって、権利があるにも拘らず何らかの理由で抽選に参加できなかったことは 500 円分の機会損失に相当する。これは券を紛失した場合や削らないまま有効期限を過ぎてしまった場合でも同様の損失額である。
印刷ミスはくじ運営者側の不備であるため一般的にこのようなケースでは返金処理になるだろう。通念としてはスクラッチくじの購入額 (例1で言えば 550 円) を返金することになるが、もし「他の購入者との機会の公平さ」を重視するのであれば期待値である 500 円が妥当な金額である。例えば「株主優待で 250 円で手に入れた報酬期待値 500 円のくじ」の不備で 250 円を返金することは、他の 250 円で手に入れた株主と比べて優待の権利を得られていないことになる。
例 3 . あなたは 20 人の部署に属している。会社の忘年会で部署ごとに一名 10,000 円が当たるゲームを開催することとなった。しかし、あなたの部署では年末進行の業務が残っており、これを担当する一名は必然的にゲームに参加することができない。この年末業務の担当者が被る損失はいくらだろうか?
これも前の例と同様に 500 円となるだろうか? 答えはノーである。
このケースでは「20 人の部署」という母集団の前提があることに注意しなければならない。担当者一名が参加できなくなることで母集団のサイズは 19 人となり、ゲームの報酬期待値は \(\frac{10000}{19}=526\) 円に上昇する (端数は切り捨てとする)。もしあなたが年末業務の担当となれば、参加すること自体に 526 円の価値があるゲームに参加できないことによって 526 円相当の機会損失を被ることになる。
会社は同一部署内でのこの不公平さを正すために、年末業務の担当者には機会損失分の 526 円を補填するべきであろう。
期待値による公平性の導入
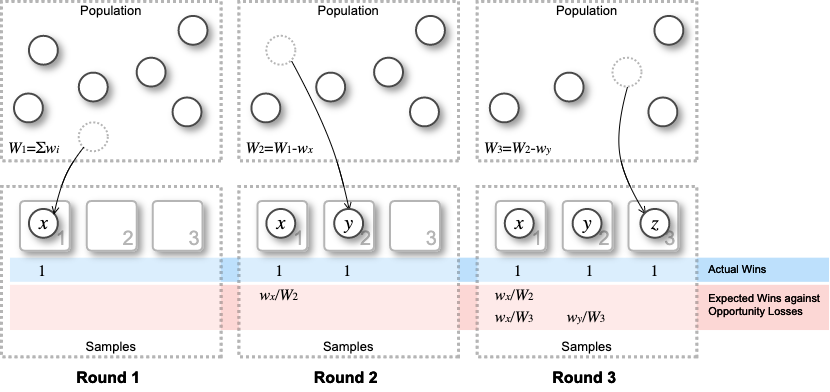
非復元ランダムサンプリングについて注意深く考えると「選択された要素がそれ以降の抽選に参加することができない」という暗黙の機会損失を前提としていることに気づくだろう。これを Fig 1 の例としてサイズ 7 の母集団から 3 つの要素を選択する課程で説明しよう。
一回目の抽選は 7 個の母集団から要素 \(x\) が選択され、\(x\) には勝数 1 が配当されている。この抽選ではどの要素も機会損失は受けておらず公平である。
二回目の抽選は \(x\) を除く 6 個の母集団から要素 \(y\) が選択され、\(y\) には勝数 1 が配当されている。ここで注目すべき点が 2 つある:
- 一回目の抽選で選択された要素 \(x\) は二回目の抽選に参加できておらず、抽選に参加できた他の要素と比較して機会損失を被っている。
- 抽選は母集団から \(x\) が除外された状態で行われたことから、母集団全体の重みが \(W_1-w_x\) に減少し、それに伴い各要素の選択期待値が一回目より上昇している。
結果的に、一回目の抽選で選択された \(x\) は二回目の抽選に参加できなかったことで当選期待値 \(\frac{w_x}{W_1-w_x}\) 相当の機会損失を受けたことになる。
三回目の抽選は \(x\), \(y\) を除く 5 個の母集団から要素 \(z\) が選択され、\(z\) には勝数 1 が配当されている。この抽選では \(x\) と \(y\) がそれぞれ当選期待値 \(\frac{w_x}{W_1-w_x-w_y}\), \(\frac{w_y}{W_1-w_x-w_y}\) 相当の機会損失を受けたことになる。一方で、\(z\) 及び他の選択されなかった要素は 3 回全ての抽選機会を得ているため機会損失はゼロである。
この例により早期に選択された要素は抽選が進むにつれて機会損失が加算されてゆくことが分かるだろう。ここで紹介する方法は、選択済みの要素が被った機会損失分を期待値に換算し加算することによって公平化するという考え方に基づいている。
機会損失モデルにおける公平性の定式化
\(n\) 個の要素で構成される母集団 \(G\) から非復元ランダムサンプリングによる繰り返し乱択で \(m\) 個の標本集合 \(\widehat{G}\) を選択する。このとき要素 \(i \in G\) には重み \(w_i\) が割り当てられているものとする (重みなしの場合はすべての \(i\) に対して \(w_i=1\) とする)。要素の重みの総和を \(W=\sum_{i=1}^n w_i\) とする。
ここで \(1 \ge r \ge m\) 回目の抽選を行う時点での \(\widehat{G}_r\) の重みの総量 (つまり \(r-1\) 回目までに選択された要素の重みの総量) を \(\widehat{W}_r\) で表すと、\(r\) 回目の抽選における要素 \(i\) の選択期待値 \(p_{i,r}\) は式 (\(\ref{probability}\)) で表すことができる。\[ \begin{eqnarray} \widehat{W}_r & = & \sum_{j \in \widehat{G}_r} w_j \nonumber \\ p_{i,r} & = & \frac{w_i}{W - \widehat{W}_r} \label{probability} \end{eqnarray} \]
選択された要素は \(G\) から \(\widehat{G}\) に移動し戻ることはない。\(r\) が大きくなるにつれて \(W\) は減少し \(\widehat{W}\) が増加することから、あとの抽選になるほど \(G\) に残されている要素の選択期待値は増加する。
\(r\) 回目の抽選で当選した要素 \(i\) には、実際の選択数 1 に加えて、残りの \(r+1\) から \(m\) までの抽選に参加できなかった機会損失をそれぞれの抽選の選択期待値で補填する。つまり、\(r\) 回目の抽選で選択された要素 \(i\) は最終的に (\(\ref{expected_selection_count}\)) に示す選択回数期待値 \(s_{i,r}\) を得る。\[ \begin{equation} s_{i,r} = 1 + \sum_{k=r+1}^m p_{i,k} = 1 + w_i \sum_{k=r+1}^m \frac{1}{W-\widehat{W}_k} \label{expected_selection_count} \end{equation} \] 前述シミュレーションの Cumulative Sum における Corrected Win Rate は式 (\(\ref{expected_selection_count}\)) による補正値を示している。このシミュレーションからも選択回数期待値が定性的に要素の重みを反映していることが見て取れるだろう。なお Reservoir アルゴリズムでは考え方が異なるため適用方法は未解決である。
実際の選択回数 1 に加算される、残り抽選での選択回数期待値の項を補正項 \(c_{i,r}\) として (\(\ref{correction_term}\)) で表す。\[ \begin{equation} c_{i,r} = w_i \sum_{k=r+1}^m \frac{1}{W-\widehat{W}_k} \label{correction_term} \end{equation} \] 試行を復元サンプリングに置き換えたときに重複選択の発生しやすい \(n\), \(m\) の組み合わせではこの補正項の影響も大きくなる。1 億人から 2 人を選ぶケースでは \(W\) が巨大であることから補正項はほぼゼロとみなして良いが、3 人から 2 人を選ぶケースでは先に選ばれた人の補正項 \(c_{i,1}\) は 1/2 となる。
この選択回数期待値 \(s_{i}\) は復元サンプリングで発生する重複選択の回数を期待値として表現しているとも考えることができる。したがって、この方法は有限回数の抽選で必ず \(m\) 個の標本を選択する保証がありながら、なおかつ選択回数期待値 \(s_i\) によって機会公平性をもたらすアルゴリズムと言える。
選択回数期待値 \(s_i\) は意味的に復元サンプリングにおける重複選択回数に相当することから、報酬配分や発言力、投票数、責務の配分比率やプライオリティといった係数として使用することができる。例えば当選 1 回相当に報酬額 \(\alpha\) を支払う抽選では、当選者 \(i\) に式 (\(\ref{expected_reward}\)) で表される期待値によって補正された報酬額を支払うことで、\(i\) に割り当てられた重み \(w_i\) に従った報酬配分に調整することができる。\[ \begin{equation} \alpha \ s_{i,r} = \alpha \left(1 + w_i \sum_{k=r+1}^m \frac{1}{W-\widehat{W}_k} \right) \label{expected_reward} \end{equation} \]
重みのない一様ランダムサンプリングでもこのような機会損失による偏りは発生している。ただし、選択されやすさに偏りがないことから、どの要素も一様に先にも後にも選択され、繰り返し実行することで均等に機会損失が累積されて現象として現れていなように見えるだけである。
この方法は当選頻度そのものには偏りを持ったままであることに注意。この偏りを報酬 (または責務、作業負荷、発言力、プライオリティとも表現できる) によって公平となるように補正する方法である。