論文翻訳: Chord: A Scalable Peer-to-peer Lookup Service for Internet Applications
Ion Stoica*, Robert Morris, David Karger, M. Frans Kaashoek, Hari Balakrishnan †
MIT Laboratory for Computer Science
chord@lcs.mit.edu
http://pdos.lcs.mit.edu/chord
 Abstract
Abstract
P2P アプリケーションが直面している根本的な問題は特定のデータ項目を格納するノードを効率的に見つけることである。この論文ではその問題を解決する分散型探索プロトコルである Chord を紹介する。Chord はキーが与えられるとそのキーをノードにマッピングするという一つの操作のみをサポートしている。それぞれのデータ項目にキーを関連付け、キーとデータ項目のペアをキーがマッピングされたノードに格納することで Chord 上にデータのロケーションを簡単に実装することができる。Chord はまたノードがシステムに参加したり離脱するのに合わせて効率的に適応し、システムが継続的に変化している場合でもクエリーに応答することができる。理論的な解析、シミュレーション、および実験の結果から Chord はスケーラブルであり、通信コストと各ノードが保持する状態は Chord のノード数に応じて対数的にスケールすることが示されている。
Table of Contents
- Abstract
- 1. 導入
- 2. 関連する研究
- 3. システムモデル
- 4. 基本 Chord プロトコル
- 5. 並行操作と障害
- 6. シミュレーションと実験結果
- 7. 今後の研究
- 8. 考察
- Acknowledgements
- 参考文献
- 翻訳抄
- *University of California, Berkeley. istoica@cs.berkeley.edu
- †アルファベット逆順の著者名
 1. 導入
1. 導入
P2P システムとアプリケーションは中央集権的なコントロールや階層的な組織を持たない分散システムであり、各ノードで動作するソフトウェアは機能的に同等である。最近の P2P アプリケーションの機能を見ると、冗長化ストレージ、永続性、近隣ノード検索、匿名化、検索、認証、また階層的な名前付け等が挙げられる。このように豊富な機能にも拘らず、ほとんどの P2P システムのコアとなる操作はデータ項目の効率的な配置である。この論文の寄稿はノードの参加と離脱が頻繁に行われる動的な P2P システム探索のためのスケーラブルなプロトコルである。
Chord プロトコルは与えられたキーに対してノードをマッピングするという一つの操作のみをサポートしている。Chord を使用するアプリケーションによっては、そのノードはキーに関連付けられた値を格納する責任を負っているかも知れない。Chord は Consistent Hashing [11] を使用して Chord ノードにキーを割り当てる。Consistent Hashing は各ノードがほぼ同数のキーを担当し、ノードがシステムに参加または離脱するときのキーの移動が比較的少ないことから、負荷分散を行う傾向がある。
過去の Consistent Hashgin に関する研究では各ノードがシステム内の他のノードを認識していることを前提としていたためノード数を大きくスケールアップすることは現実的ではなかった。対照的に Chord の各ノードが必要とするのは他の少数のノードに関する "ルーティング" 情報だけである。ルーティングテーブルは分散されているため、ノードは他の少数のノードと通信することでハッシュ機能を解決する。\(N\) ノードで構成されるシステムでは、各ノードは定常状態で他のノードに関する \(O(\log N)\) の情報のみを保持し、他のノードへの \(O(\log N)\) メッセージを介してすべての探索を解決する。Chord はノードがシステムに参加または離脱するときにそのルーティング情報を保守する; このようなイベントはほとんどの場合 \(O(\log^2 N)\) メッセージ以下で行われる。
Chord を他の多くの P2P 探索プロトコルと区別する 3 つの特徴は、そのシンプルさ、証明可能な正確さ、そして証明可能なパフォーマンスである。Chord はシンプルに \(O(\log N)\) ノードを経由してキーを目的のノードに向けてルーティングする。Chord のノードは効率的なルーティングのために他の \(O(\log N)\) ノードに関する情報を必要とするが、その情報が古くなるとパフォーマンスは緩やかに低下する。これは、ノードが任意のタイミングで参加または離脱することにより \(O(\log N)\) 状態の一貫性を保守することが困難となりうることから実際に重要な問題である。Chord においてクエリーの正しい (ただし遅い) ルーティングを保証するためには、ノードごとに少なくとも 1 つの正しい情報が必要となる。
本稿の残りの部分は以下のように構成されている。Section 2 では Chord と関連する研究を比較する。Sesion 3 では Chord プロトコルの動機となったシステムモデルを紹介する。Section 4 では基本となる Chord プロトコルを提示していくつかの特性を証明する。Section 6 ではシミュレーションとプロトタイプを用いた実験によって Chord の性能に関する我々の主張を実証する。Section 7 では今後の研究のための項目を概説し Section 8 で我々の寄稿をまとめる。
 2. 関連する研究
2. 関連する研究
Chord はキーをノードにマッピングするが、従来の名前とロケーションサービスはキーと値を直接マッピングする。値はアドレス、文書または任意のデータ項目を指定することができる。Chord ではそれぞれのキー/値ペアをそのキーがマッピングされているノードに格納することでその機能を簡単に実装することができる。この理由により、また比較をより明確にするために、この章の残りの部分ではキーを値にマッピングする Chord ベースのサービスを仮定する。
DNS はホスト名と IP アドレスのマッピングを提供する [15]。Chord ではキーを名前で、値を関連する IP アドレスで表せばで同じサービスを提供することができる。DNS は特別なルートサーバの集合に依存している。DNS 名は管理の境界を反映するように構造化されているが Chord は命名構造を課していない。DNS は名前のつけられたホストやサービスを探索することに特化しているが、Chord は特定のマシンに縛られていないデータオブジェクトを見つけるためにも使用することができる。
Freenet の P2P ストレージシステム [4,5] は Chord と同様に分散型で対象性がありホストの離脱や参加に対して自動的に適応する。Freenet は文書の担当を特定のサーバには割り当てず、その代わりにキャッシュされたコピーを検索する形をとっている。これにより Freenet はある程度の匿名性を提供することができるが、実在する文書の検索を検索コストを低く抑えたりすることはできない。Chord は匿名性を提供しないがその検索操作は予測可能な時間内に実行され、常に成功または決定論的な失敗という結果をもたらす。
Ohaha システムは文書をノードにマッピングするための Consistent Hashgin に似たアルゴリズムと Freenet 形式のクエリールーティングを使用している [18]。その結果 Freenet の欠点のいくつかを共有している。Archival Intermemory はオフラインで計算されたツリーを使用して論理アドレスをデータを保存するマシンにマッピングする [3]。
Globe システム [2] は移動するオブジェクトの位置にオブジェクト識別子をマッピングする広域位置情報サービスを持っている。Globe ではインターネットを地理、トポロジー、または管理ドメインの階層として配置し、DNS のように静的で世界規模の探索木を効率的に構築する。オブジェクトに関する情報は特定のリーフドメインに格納され、ポインタのキャッシュは検索のショートカットを提供する [22]。Globe システムはハッシュのような技術を使って複数の物理ルートサーバ間でオブジェクトを分割することで論理ルートサーバの高負荷に対処する。Chord はこのハッシュ機能を十分うまく実行しているため階層構造を成さずにスケーラビリティを実現することができているが、Chord は Globe ほどネットワーク局所性を利用しない。
Plaxton らによって開発された分散データロケーションプロトコル [19] (OceanStore [12] で使われている変種) はおそらく最も Chord に近いプロトコルである。これは Chord よりも強力な保証を提供する。Chord と同様にクエリーが対数ホップとなることとキーの分散が取れていることを保証するが、Plaxton プロトコルでは、ネットワーク・トポロジーの仮定のもとで、キーを保存しているノードよりもネットワーク距離が遠くなるようなクエリーの転送が起きないことを保証している。Chord の利点は複雑さが大幅に少なく、同時接続ノードの接続や失敗をうまく処理できる点である。Chord プロトコルは PAST [8] で使用されている位置情報アルゴリズムである Pastry にも似ているが、Pastry は Prefix ベースのルーティングであり他の詳細な点で Chord とは異なる。
CAN は (ある固定の \(d\) に対して) \(d\) 次元デカルト座標空間を使用してキーを値にマッピングする分散ハッシュテーブルを実装している [20]。各ノードは \(O(d)\) の状態を保持し探索コストは \(O(d N^{\frac{1}{d}})\) である。したがって、Chord とは対照的に CAN のノードが保持する状態はネットワークサイズ \(N\) に依存しないが探索コストは \(\log N\) より速く増加する。\(d = \log N\) であれば CAN の探索時間とストレージは Chord と同じ量を必要とする。しかし CAN は \(N\) の変化に応じて \(d\) を変化させる (したがって \(\log N\)) ように設計されていないため、この一致は固定された \(d\) に対する "正しい" \(N\) に対してのみ起きる。また Chord には部分的に不正確なルーティング情報に遭遇してもその正しさが堅牢であるという利点がある。
Chord のルーティング手順は Grid 位置情報システム [14] の 1 次元アナログと考えることができる。Grid はクエリーのルーティングを実世界の地理的位置情報に依存しているが、Chord はノードを人工的な 1 次元空間にマップし、その中で Grid と同様のアルゴリズムでルーティングが行われる。
Chord は Section 3 で説明するように様々なシステムを実装するための検索サービスとして使用することができる。特に Napster のようなシステム [17] が持つ単一障害点や単一コントロールや、Gnutella のようなシステム [10] でブロードキャストを多用しているために顕在化するスケーラビリティの欠如を回避するのに役立つ。
 3. システムモデル
3. システムモデル
Chord は以下のような困難な問題に対処することで P2P システムやそれに基づくアプリケーション設計を簡素化する:
- 負荷分散: Chord は分散ハッシュ機能として動作しキーをノード間で均等に分散させる; これにより自然に負荷分散が得られる。
- 分散化: Chord は完全に分散されている: どのノードも他のノードより重要ではない。これによりロバスト性が向上し Chord をゆるく組織化された (looseely-organized) P2P アプリケーションに適合させている。
- スケーラビリティ: Chord の探索コストはノード数の対数に比例して増加するため、非常に大規模なシステムであっても実現可能である。このスケーリングを実現するためにパラメータのチューニングは必要ない。
- 可用性: Chord は、ノードの障害だけでなく新たに参加するノードを反映するように内部テーブルを自動調整し、基礎となるネットワークに重大な障害が発生しない限りキーを担当するノードを見つけることができる。これはシステムが継続的に変化している場合でも同様である。
- 柔軟な命名: Chord は検索するキーの構造に制約がない: コードのキー空間はフラットである。このためアプリケーションはそれら自身の名前をどのように Chord のキーにマッピングするかについて大きな柔軟性を持つことができる。
Chord ソフトウェアはそれを使用するクライアントおよびサーバアプリケーションとリンクされるライブラリの形式を取る。アプリケーションは主に 2 つの方法で Chord と対話する。第一に、Chord はキーを担当するノードの IP アドレスを取得する (キー) 探索アルゴリズムを提供する。第二に、各ノード上の Chord ソフトウェアはそのノードが担当しているキー集合のヘンクをアプリケーションに通知する。これによりアプリケーションソフトウェアは、例えば新しいノードが参加した時に対応する値を新しいホームに移動させることができる。
Chord を使用するアプリケーションは、必要とされる認証、キャッシュ、レプリケーション、そしてデータに対するユーザフレンドリーな命名を提供する必要がある。Chord のフラットなキー空間はこれらの機能の実装を容易にする。例えばアプリケーションはデータの暗号化ハッシュから派生した Chord キーに基づいてデータを格納することでデータを認証することができる。同様に、データに対するアプリケーションレベルの識別子から派生した 2 つの異なる Chord キーに基づいてデータを格納することでアプリケーションはデータを複製する事ができる。
以下は Chord が良い基盤となるだろうアプリケーションの例である:
- 最近の提案 [6] で概説されている協調ミラーリング (cooperative mirroring)。ディストリビューションを公開したいと考えている開発者たちを想像してください。それぞれのディクトリビューションに対する需要は、新しいリリース直後の非常に人気のあるものから比較的人気のないものまでリリース間で劇的に変化するかもしれない。このための効率的なアプローチは開発者が協力して互いのディストリビューションをミラーリングすることだろう。理想的には、ミラーリングシステムはすべてのサーバ間で負荷分散をとり、データの複製とキャッシュを行い、真正性を保証するだろう。このようなシステムは本誌ステキな中央管理がないため信頼性の観点から完全に分散化されるべきだろう。
- とぎれとぎれな接続性を持つノードのための時間共有ストレージ。ある人が特定のデータを常に利用できるようにしたいが、その人のマシンが時々しか利用できないとき、マシンがアップしているときに他のユーザのデータを保存する代わりに、ダウンしている時は他のユーザのマシンに保存するように提案できる。データの名前は、任意のタイミングでデータ項目を保存する担当の (ライブ) Chord ノードを識別するためのキーとして機能する。Cooperative Mirroring アプリケーションと同様に大きの問題が発生するが、ここでは負荷分散よりも可用性に焦点を当てている。
- Gnutella や Napster のようなキーワード検索をサポートする分散インデックス。このようなアプリケーションではキーは希望するキーワードから導出され、値はそのキーワードを持つ文書を提供するマシンのリストとなる。
- 大規模な組み合わせ検索、例えば暗号解読 (code breaking)。この場合、キーは問題を解くための候補 (暗号鍵など) であり、Chord はこれらのキーを解くためのテストを行うマシンにマッピングする。
Figure 1 は協調ミラーリングシステムに対して可能な 3 層構造ソフトウェアを表している。最上層ではユーザにファイルのようなインターフェースを提供し、ユーザフレンドリーな名前付けや認証を行う。この "ファイルシステム" 層は名前付きのディレクトリとファイルを実装し、それらに対する操作を低レベルのブロック操作にマッピングする。次の層の "ブロックストレージ" はブロックの操作を実装する。この層はブロックの保存、キャッシュ、レプリケーションを行う。ブロックストレージ層は Chord を使用してブロックを格納するノードを特定し、そのノード上のブロックストレージサーバと通信してブロックの読み書きを行う。
 4. 基本 Chord プロトコル
4. 基本 Chord プロトコル
Chord プロトコルではキーのロケーションを探す方法、新しいノードがシステムに参加する方法、既存のノードの障害 (または計画された離脱) から回復する方法を指定する。このセクションでは、参加と障害が同時に発生しない簡易的なプロトコルについて説明する。Section 5 では同時に発生する参加と障害を扱うための基本プロトコルの拡張について説明する。
 4.1 概要
4.1 概要
Chord の中核は、キーとそれらを担当するノードをマッピングするハッシュ関数の高速な分散計算である。Chord は Consistent Hashing [11, 12] を使用しており、これにはいくつかの優れた特性がある。ハッシュ関数は高確率で負荷を分散する (すべてのノードがほぼ同じ数のキーを引き受ける)。\(N\) 番目のノードがネットワークに参加 (または離脱) したときも、高確率でキーの \(O(1/N)\) のみが別のロケーションに移されるだけである ─ これは明らかに負荷分散を維持するために必要な最小限である。
Chord はすべてのノードが他のすべてのノードを認識しているという条件を避けることで Consistent Hashing のスケーラビリティを向上させている。Chord のノードが必要とするのは他のノードに関するわずかな "ルーティング" 情報だけである。この情報は分散されているため、ノードは少数の他のノードと通信することでハッシュ関数を解決する。\(N\) ノードからなるネットワークでは、他のノードは \(O(\log N)\) ノードに関する情報のみを保持しており、検索には \(O(\log N)\) のメッセージが必要である。
ノードがネットワークに参加したり離脱するとき、Chord はルーティング情報を更新しなければならない; 参加や離脱には \(O(\log^2 N)\) メッセージが必要である。
 4.2 Consistent Hashing
4.2 Consistent Hashing
Consistent Hashing 関数は SHA-1 [9] のような基本ハッシュ関数を使用して各ノードとキーに \(m\) ビットの識別子を割り当てる。ノードの識別子はノードの IP アドレスをハッシュ化して生成し、キーの識別子はキーをハッシュ化して生成する。ここで我々は文脈での意味が明確となるように元のキーとハッシュ関数での写像の両方を指すために "キー" という用語を使うことにする。同様に "ノード" という用語はハッシュ関数の下でのノードとその識別子の両方を指すことにする。識別子の長さ \(m\) は 2 つのノードやキーが同じ識別子にハッシュ化される確率が無視できるほど大きくなければならない。
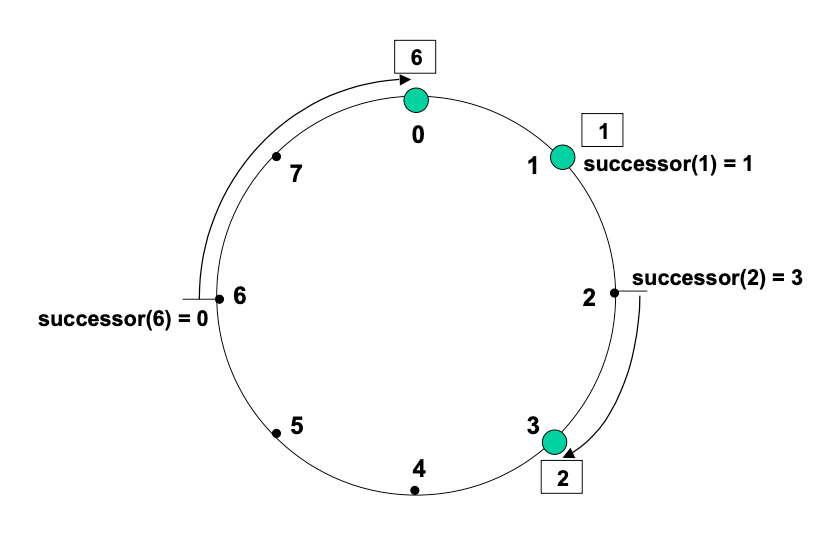
Consistent Hashing は次のようにしてキーをノードに割り当てる。識別子は \(2^m\) を法とする識別子円 (identifier circle) 上で順に並べられる。キーは識別子空間内で識別子 \(k\) と等しいかそれに続く (識別子の) 最初のノードに割り当てられる。このノードはキー \(k\) の後続者ノード (successor node) と呼ばれ \({\it successor}(k)\) と表記される。識別子を 0 から \(2^m-1\) までの数字の円で表現すると \(k\) から時計回りに見て最初のノードとなる。
Figure 2 は \(m=3\) の識別子円を示している。この円には 0, 1, そして 3 の 3 つのノードがある。識別子 1 のノードの後継ノードは 1 であるためキー 1 はノード 1 に配置される。同様に、キー 2 はノード 3 に、キー 6 はノード 0 に配置される。
Consistent Hashing はノードがネットワークに参加または離脱するときの混乱を最小限に抑えるように設計されている。ノード \(n\) がネットワークに参加したとき Consistent Hashing のマッピングを維持するために、以前は \(n\) の後続者ノードに割り当てられていた特定のキーが \(n\) に割り当てられるようになる。ノードへのキーの割り当て以外に変更を加える必要はない。前述の設定に識別子 7 のノードが参加すると識別子 0 のノードから識別子 6 のキーが取り込まれる (訳注: 本質的には 4 から 7 の範囲のキーだが、前述の例で挙げたキー 1, 2, 6 のうち 6 のみが移動するという意味)。
以下の結果は Consistent Hashing を導入した論文 [11, 13] で証明されている:
定理 1. \(N\) 個のノードと \(K\) 個のキーのどのような集合であっても、高い確率で:
- それぞれのノードは最大でも \((1+\epsilon)K/N\) 個のキーを担当する。
- \((N+1)\) 番目のノードが参加または離脱するとき、\(O(K/N)\) 個のキーの担当が (参加ノードへまたは離脱ノードからのみ) 移動する。
前述のように Consistent Hashing を実装した場合、この定理は \(\epsilon=O(\log N)\) の範囲を証明する。Consistent Hashing の論文では、各ノードが独自の識別子を持つ \(O(\log N)\) の "仮想ノード" を実行することで \(\epsilon\) を任意の小さな定数に削減できることが示されている。
"高い確率で" という言葉には議論の余地がある。簡単な解釈としてはノードとキーがランダムに選ばれているということである。これは敵対性のない世界のモデルとしてもっともである。確率分布はキーとノードのランダムな選択に対するものとなり、そのような乱択が不均衡な分布を生成する可能性は低いと言われている。しかし、敵対者が同じ識別子にハッシュ化されるキーを意図的に選択することで負荷分散の性質を破壊するのではないかと心配するかもしれない。Consistent Hashing 論文では "\(k\)-ユニバーサルハッシュ関数" を使用してランダムではない鍵の場合でも一定の保証を提供している。
我々は \(k\)-ユニバーサルハッシュ関数ではなく標準の SHA-1 関数をベースのハッシュ関数として使用することにした。これにより我々のプロトコルは決定論的なものとなり "高い確率で" という主張はもはや意味をなさない。しかし SHA-1 の下で衝突するキーの集合を生成することは、ある意味で SHA-1 関数の反転操作、つまり "復号化" とみなすことができる。これは困難であると考えられている。したがって、我々の定理が高い確率で維持されることを述べる代わりに "標準的な困難性の仮定に基づき" 維持されると主張することができる。
(主に表現を) 簡単にするために仮想ノードの説明を省略する。この場合、ノードの負荷は高い確率で (あるいは我々の場合では標準的な困難性の過程に基づいて) 平均を (最大で) 係数 \(O(\log N)\) だけ超える可能性がある。仮想ノードの使用を避ける理由の一つは、必要とされる数がシステム内のノード数によって決まるため、決定することが難しい場合があるためである。もちろん、システム内のノード数の自明な上限を利用することもできる; 例えば IPv4 アドレスあたり最大 1 つの Chord サーバを想定することができる。この場合、物理ノードごとに 32 個の仮想ノードを実行することで良好な負荷分散が得られる。
 4.3 スケーラブルなキーロケーション
4.3 スケーラブルなキーロケーション
分散環境で Consistent Hashing を実装するには非常に少量のルーティング情報で十分である。各ノードは円上の後続者ノードだけを認識していれば良い。与えられた識別子に対するクエリーは、その識別子の最初の後続者ノード (これはクエリーがマップするノードである) に到達するまでそれらの後続者ノードのポインターを渡って円内を移動することができる。Chord プロトコルの一部ではこれらの後続者ポインターを維持することですべての探索が正しく解決されることが保証されている。しかしこの解決方法は、適切なマッピングを見つけるためには \(N\) 個のノードすべてを走査しなければならない可能性があることから非効率的である。このプロセスを高速化するために Chord は追加のルーティング情報を保持している。後続者の情報が正しく維持されている限りルーティングの正確性は維持されるためこの追加情報は必須ではない。
前述のようにキーまたはノード識別子のビット数を \(m\) とする。各ノード \(n\) はフィンガーテーブルと呼ばれる (最大でも) \(m\) 個のエントリを持つルーティングテーブルを保持している。ノード \(n\) のテーブルの \(i\) 番目のエントリには、識別子円上で \(n\) から少なくとも \(2^{i-1}\) 以上先の最初のノード \(s\) の ID が含まれている。つまり \(s={\it successor}(n+2^{i-1})\) である。ここで \(1 \le i \le m\) とする (そしてすべての算術は \(2^m\) を法とする)。我々はノード \(s\) をノード \(n\) の \(i\) 番目の finger と呼び \(n.{\it finger}[n].{\it node}\) と表記する (Table 1 参照)。finger テーブルのエントリには該当するノードの Chord 識別子と IP アドレス (およびそのポート番号) の両方が含まれている。\(n\) の最初の finger は円上でのすぐ後ろのノードであることに注意; 便宜上、我々はしばしば最初の finger ではなく後続者と呼ぶことがある。
| Notation | Definition |
|---|---|
| \({\it finger}[k].{\it start}\) | \(n+2^{k-1} \bmod 2^m, 1 \le k \le m\) |
| \(\ \ .{\it interval}\) | \([{\it finger}[k].{\it start}, {\it finger}[k+1].{\it start})\) |
| \(\ \ .{\it node}\) | first node \(\ge n.{\it finger}[k].{\it start}\) |
| \({\it successor}\) | the next node on the identifier circle; \({\it finger}[1].{\it node}\) |
| \({\it predecessor}\) | the previous node on the identifier circle |
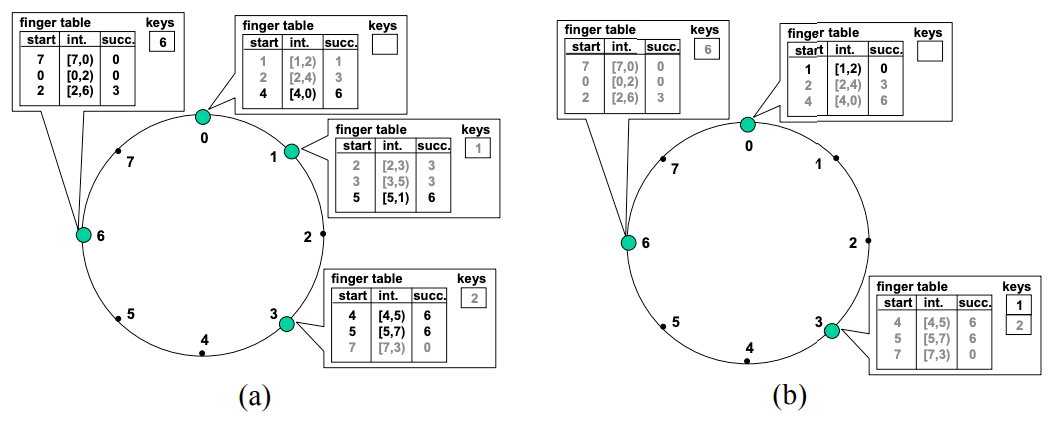
Figure 3 (b) に示す例では、ノード 1 の finger テーブルは識別子 \((1+2^0) \bmod 2^3=2\), \((1+2^1) \bmod 2^3=3\), \((1+2^2) \bmod 2^3=5\) をそれぞれ後続者ノードとして指している。識別子 2 の後続者は、2 に続く最初のノードとなるノード 3 である。識別子 3 は (自明に) ノード 3 であり、5 の後続者ノードはノード 0 である。

この方法には 2 つの重要な特徴がある。第一に、各ノードは他のノードに関して少数の情報のみを格納しており、識別子円上で自分の近く続くノードに関してはより離れたノードよりも多くのノードを知っている。第二に、ノードの finger テーブルは一般に任意のキー \(k\) の後続者ノードを決定するのに十分な情報を含んでいない。例えば、Figure 3 のノード 3 は 1 の後続者 (ノード 1) がノード 3 の finger テーブルに現れないため 1 の後続者を知らない。
あるノードがキー \(k\) の後続者を知らない場合はどうなるだろうか? もし \(n\) が自分の ID よりも \(k\) に近いノードを見つけることができるのであれば、そのノードは \(n\) よりも \(k\) の領域の識別子円についてより多くの情報を知っているはすである。したがって、\(n\) は finger テーブルから ID が \(k\) の直前にあるノード \(j\) を検索し、ノード \(j\) に ID が \(k\) に最も近い既知のノードを問い合わせる。このプロセスを繰り返すことにより \(n\) は ID が \(k\) に近いノードについて学習する。
この探索プロセスを実装した擬似コードを Figure 4 に示す。表記 \(n.{\it foo}()\) はノード \(n\) で呼び出され実行される関数 \({\it foo}()\) を表している。リモートへの呼び出しや変数参照の前にはリモートノードの識別子を付けているが、ローカルの呼び出しや変数参照ではローカルノードを省略している。したがって \(n.{\it foo}()\) はノード \(n\) 上のリモートプロシジャーコールを表し、\(n.{\it bar}\) はノード \(n\) 上の変数 \({\it bar}\) を探すための RPC である。

\({\it find\_successor}\) は目的の識別子の直前のノードを見つけることで機能する; そのノードの後続者は識別子の後続者でなければならない。我々は後述する参加の操作 (Section 4.4) を実装するために使う \({\it find\_predecessor}\) を明示的に実装している。
ノード \(n\) が \({\it find\_predecessor}\) を実行すると Chord 円の周囲を \({\it id}\) に向かって前進する一連のノードと接触する。もし \({\it id}\) が \(n'\) と \(n'\) の後続者の間に位置するようなノード \(n'\) にノード \(n\) が接触した場合、\({\it find\_predecessor}\) が実行され \(n'\) が返される。そうでなければノード \(n\) は \(n'\) が知っているノードの中で \({\it id}\) に最も近いものを \(n'\) に尋ねる。このようにしてアルゴリズムは常に \({\it id}\) の precedessor に向かって進む。
例として Figure 3(b) の Chord 円について考える。ノード 3 が識別子 1 の後続者を見つけようとしている。ノード 1 が円形区間 \([7,3)\) に属しているため \(3.{\it finger}[3].{\it interval}\) に属している; したがってノード 3 は finger テーブルの 3 番目のエントリである 0 を確認する。0 は 1 より前にあるためノード 3 はノード 0 に 0 の後続者を見つけるよう要求する。一方でノード 0 は自分の finger テーブルから 1 の後続者がノード 1 自身であると推察しノード 1 をノード 3 に返す。
円周距離の倍化を繰り返す finger ポインタにより \({\it find\_predecessor}\) でのループが繰り返されるたびに、目的の識別子までの距離が半分に鳴る。この直感は以下の定理に従う:
定理 2. 高い確率で (あるいは標準的な困難性の仮定の下で) \(N\)-ノードのネットワークで後続者を見つけるために接触しなければならないノード数は \(O(\log N)\) である。
証明. ノード \(n\) が \(k\) の後続者に対する問い合わせを解決しようとしていると想定する。\(p\) を \(k\) の直前のノードとし、我々はクエリーが \(p\) に到達するまでのステップ数を分析する。
前述の通り \(n \ne q\) であれば \(n\) は自身の finger テーブルの中で最も \(k\) に近い先行者 (predecessor) にクエリーを転送する。ノード \(n\) の \(i\) 番目の finger 区間にノード \(p\) があるとする。このとき、この区間は空ではないためノード \(n\) はこの区間内のノード \(f\) を指している。\(n\) と \(f\) の距離 (識別子の数) は少なくとも \(2^{i-1}\) である。しかし \(f\) と \(p\) はどちらも \(n\) の \(i\) 番目の finger 区間にあり、その距離は最大でも \(2^{i-1}\) である。これは \(f\) が \(n\) よりも \(p\) に近いことを意味している。つまり \(f\) から \(p\) までの距離は最大でも \(n\) から \(p\) までの距離の半分であることを意味している。
クエリーを処理しているノードと先行者 \(p\) の距離がそれぞれのステップで半分になり、初期の距離が最大でも \(2^m\) であれば、\(m\) ステップ以内に距離は 1 となり \(p\) に到着したことを意味する。
事実、前述のようにノードとキーの識別子はランダムであると仮定すると、必要な転送の数は高確率で \(O(\log N)\) となるだろう。\(\log N\) 回の転送のあと、現在のクエリーノードとキー \(k\) の距離は最大でも \(2^m/N\) に減少する。このサイズの範囲に到達するノード識別子数の期待値は 1 であり、高確率で \(O(\log N)\) である。したがって残りのステップが一度に一つのノードだけ進んだとしても、残りのステップは残りの区間全体を横切り、さらに \(O(\log N)\) ステップ内でキー \(k\) に到達することになる。∎
実験結果を報告する章 (Section 6) では平均探索時間が \(\frac{1}{2} \log N\) であることを観察 (および正当化) する。
 4.4 ノードの参加
4.4 ノードの参加
動的なネットワークではノードはいつでも参加 (および離脱) することができる。これらの操作を実装する際の主な課題は、ネットワーク内のすべてのキーを特定する機能を維持することである。この目的を達成するために Chord は 2 つの不変条件 (invariant) を維持する必要がある。
- 各ノードの後続者が正しく維持されていること。
- すべてのキー \(k\) に対してノードの \({\it successor}(k)\) が \(k\) を担当していること。
探索を高速に行うためには finger テーブルが正しいことも望ましい。
この章では単一のノードが参加した場合にこれらの不変条件を維持する方法を示す。複数のノードが同時に参加するケースでの議論は Section 5 に延期し、ノードの故障をどのように処理するかについても議論する。参加操作を説明する前にその性能をまとめる (この定理の証明はテクニカルレポート [21] にある)。
定理 3. \(N\)-ノードの Chord ネットワークに参加または離脱するノードは高確率で \(O(\log^2 N)\) 回のメッセージを使用して Chord ルーティングの不変条件と finger テーブルを再確立する。
参加と離脱のメカニズムを単純化するために、Chord の各ノードは先行者ポインタを保持する。ノードの先行者ポインタはそのノードの直前の Chord 識別子と IP アドレスを含み、識別子円周を反時計回りに移動するために使用することができる。
前述の不変条件を維持するために、ノード \(n\) がネットワークに参加すると Chord は 3 つのタスクを実行しなければならない。
- ノード \(n\) の先行者と finger を初期化する。
- ノード \(n\) の追加を反映させるために既存のノードの finger と先行者を更新する。
- 上位レイヤーのソフトウェアに通知して、ノード \(n\) が新しく担当するキーに関連する状態 (値など) を転送できるようにする。
ここで我々は参加を試みるノードが何らかの外部メカニズムによって既存の Chord ノード \(n'\) の識別子を知っているものと仮定する (Chord リングに存在する既知のノード \(n'\) をブートストラップノードとして使用する)。ノード \(n\) は以下のように \(n'\) を使って状態を初期化し、既存の Chord ネットワークに自身を追加する。
finger と先行者の初期化: ノード \(n\) は Figure 6 の擬似コードを使用して \(n'\) に検索を依頼することで先行者と finger を教わる。\(m\) 個の finger エントリのそれぞれに対して単純に \({\it find\_successor}\) を実行すると \(O(m \log N)\) の実行時間が発生する。これを削減するために \(n\) は各 \(i\) について \(i\) 番目の finger が正しい \(i+1\) 番目の finger であるかどうかを確認する。これは \({\it finger}[i].{\it interval}\) がいかなるノードも含まない場合に発生し \({\it finger}[i].{\it node} \ge {\it finger}[i+1].{\it start}\) となる。この変更により検索しなければならない finger エントリの期待数が (高確率で) \(O(\log N)\) に減少し、全体の時間が \(O(\log^2 N)\) に削減されることを示している。
実用的な最適化として、新しく参加するノード \(n\) が隣接するノードに完全な finger テーブルとその先行者のコピーを尋ねることができる。\(n\) のテーブルは隣接ノードのものと似ているため、\(n\) はこれらのテーブルの内容をヒントとして使用して自分のテーブルの正しい値を見つける助けにすることができる。これは finger テーブルを埋める時間を \(O(\log N)\) に短縮できることを示している。
既存ノードの finger の更新: ノード \(n\) はいくつかの既存ノードの finger テーブルに設定される必要がある。例えば Figure 5(a) では、ノード 6 はノード 0 と 1 の 3 番目の finger であり、ノード 3 の 1 番目と 2 番目の finger となる。
Figure 6 は既存の finger テーブルを更新する \({\it update\_finger\_table}\) 関数の擬似コードを示している。ノード \(n\) は、(1) \(p\) が \(n\) より少なくとも \(2^{i-1}\) だけ先行し、(2) ノード \(p\) の \(i\) 番目の finger が \(n\) より後である場合にのみノード \(p\) の \(i\) 番目の finger となるだろう。したがって、与えられた \(n\) に対して、アルゴリズムはノード \(n\) の \(i\) 番目の finger で開始し、そして \(n\) より前の finger を持つノードに遭遇するまで識別子円上を反時計回りに移動し続ける。
技術報告 [21] では、ノードがネットワークに参加した時に更新する必要のあるノード数は高い確率で \(O(\log N)\) であることを示している。これらのノードを見つけて更新するには \(O(\log^2 N)\) の時間がかかる。より洗練されたスキームではこの時間を \(O(\log N)\) に短縮することができる; しかし我々は次の章のアルゴリズムを使用する実装を想定しているためここでその方法は提示しない。
キーの転送: ノード \(n\) がネットワークに参加した時に実行しなければならない最後の操作は、ノード \(n\) が後続者となったすべてのキーの担当を移動することである。これが何を意味するかは Chord を使用する上位レイヤーのソフトウェアに依存するが、一般的には各キーに関連付けられたデータを新しいノードに移動させることになる。ノード \(n\) は、自身が参加する前に直後のノードの担当していた鍵に対してのみ後続者となることができる。そのため \(n\) は関連するすべてのキーの担当を移転するためにその 1 つのノードにのみ通知する必要がある。
 5. 並行操作と障害
5. 並行操作と障害
現実的には Chord はノードの参加と障害または自発的な離脱を同時進行で処理する必要がある。この章ではこれらの状況を処理するために Section 4 で説明した基本的な Chord アルゴリズムの修正版について説明する。
 5.1 安定化
5.1 安定化
Section 4 の参加アルゴリズムはネットワークが発展するにしたがってすべてのノードの finger テーブルを積極的に維持する。この不変条件は大規模なネットワークにおいて同時並行の参加に直面したときに維持することが困難であるため、我々は正確性とパフォーマンスとで目標を分離している。基本的な "安定化" プロトコルを使用してノードの後続者ポインタを最新の状態に保つ。これは検索の正確性を保証するのに十分なものである。これらの後続者ポインタは finger テーブルのエントリの検証と修正に使用される。これによってこれらの検索は高速かつ正確にすることができる。
参加ノードが Chord リングのいくつかの領域に影響を与えた場合、安定化が完了する前に発生した検索は 3 つの動作のうちの 1 つを示す可能性がある。一般的なケースは、検索に関与するすべての finger テーブルのエントリが適度に最新であり、検索は \(O(\log N)\) ステップで正しい後続者を発見する場合である。2 番目のケースは、後続者ポインタは正しいが finger が不正確な場合である。これにより正しい検索は行われるが処理が遅くなる可能性がある。最後のケースでは、影響を受ける領域のノードが誤った後続者ポインターを持っているか、キーがまだ新たに参加したノードに移行していないことが原因で検索に失敗する可能性がある。Chord を使用する上位レイヤーのソフトウェアは目的のデータが見つからなかったことに気づき、一時停止後に検索を再試行することができる。安定化は後続者ポインタを素早く修正するため、この一時停止は短くても構わない。
我々の安定化スキームは、同時並行の参加、メッセージのロストや並べ替えが起きた場合でも、既存のノードの到達性を維持する方法で Chord リングにノードを追加することを保証する。安定化それ自体では、複数の不連続なサイクルに分割された Chord システムや、識別子空間の円周を複数回ループする単一のサイクルを修正することはできない。このような病的なケースは通常のノード参加のシーケンスでは発生しない。それらがネットワークの分断と回復、あるいは断続的な障害によって発生するかは不明である。もし発生した場合、これらのケースはリングトポロジーの定期的なサンプリングにより検出および修復することができる。
Figure 7 は参加と安定化のための擬似コードを示している; このコードは同時並行の参加を処理するために Figure 6 を置き換えている。ノード \(n\) が最初に起動すると \(n.{\it join}(n')\) を呼び出す。ここで \(n'\) は既知の任意の Chord ノードである。\({\it join}\) 関数は \(n'\) に \(n\) の直後の後続者を見つけるように求める。それ自体では、\({\it join}\) は残りのネットワークに \(n\) を認識させることはない。
すべてのノードは定期的に \({\it stabilize}\) を実行する (これは新しく参加したノードがネットワークに認識される方法である)。ノード \(n\) が \({\it stabilize}\) を実行すると、\(n\) の後続者に後続者の先行者 \(p\) を問い合わせ、\(p\) が \(n\) の後続者の代わりとなるかを決定する。これはノード \(p\) が最近システムに参加した場合のケースである。また \({\it stabilize}\) はノード \(n\) の後続者に \(n\) の存在を通知し、後続者に先行者を \(n\) に変更する機会を与える。後続者がこれを行うのは \(n\) よりも近い先行者がいないことを知っている場合に限る。
簡単な例として、ノード \(n\) がシステムに参加しその ID がノード \(n_p\) と \(n_s\) の間にあるとする。\(n\) はその successor として \(n_s\) を後続者として取得する。ノード \(n_s\) は \(n\) から通知を受けると先行者として \(n\) を取得する。\(n_p\) が次に \({\it stabilize}\) を実行するときに \(n_s\) に先行者 (現在は \(n\)) を問い合わせる; \(n_p\) はこのとき successor として \(n\) を取得する。最終的に \(n_p\) は \(n\) に通知し \(n\) は先行者として \(n_p\) を取得する。この時点ですべての先行者と後続者のポインタが正しいことになる。
後続者のポインタが正しいとただちに \({\it find\_predecessor}\) (したがって \({\it find\_successor}\) の呼び出しが動作する。まだ finger されていない新規に参加したノードには \({\it find\_predecessor}\) が最初は届かないかもしれないが、検索アルゴリズムのループは正しい先行者に到達するまで新規に参加したノードを介して後続者 (\({\it finger}[1]\) ポインタを追跡する。最終的に \({\it fix\_fingers}\) は finger テーブルのエントリを調整しこれらの線形スキャンの必要性を排除する。
以下の定理 (技術報告 [21] で証明されている) は同時並行の参加によってひこ起こされるすべての問題が一時的なものであることを示している。この定理は通信を試みる 2 つのノードがいずれは最終的に成功すると想定している。
定理 4. あるノードが与えられたクエリーの解決に成功すると、症例的には常に解決できるようになる。
定理 5. 最後に参加のあった後のある時点で、すべての後続者ポインタは正しくなる。
これらの定理の証明は不変条件と終了アーギュメントに依存している。不変条件は一度ノード \(n\) が後続者ポインタを介してノード \(r\) に到達できると、常に到達できることを示している。終了について論議するために 2 つのノードの両方が同じ後続者ノードを持っていると考えられるケースについて考慮する。この場合、それぞれが \(s\) に通知を試み、最終的に \(s\) は 2 つのうち近い方 (またはそれ以外のより近いノード) を先行者として選択する。この時点で遠い方の 2 つは \(s\) と接触することによって \(s\) よりも優先される後続者を知ることになる。したがって、すべてのノードは時間の経過とともにより良い後続者に向かって進行する。この進行は、すべてのノードが他の 1 つのノードの後続者ノードとみなされる状態で最終的に停止する必要がある; これはサイクルを定義する (またはサイクルのセットだが、不変条件は最大 1 つであることを保証する)。
ノードの参加時の finger の調整については、参加によって finger の性能が大きく損なわれないことが判明したためここでは説明しなかった。もしノードが各区間に finger を持っていれば参加後も引き続きその finger を使用することができる。距離を半減するアーギュメントは基本的に変更されておらず、\(O(\log N)\) ホップでクエリーの目的地に "近い" ノードに到達するには十分であることを示している。新規の参加はクエリーの目的地の古い先行者ノードと後続者ノードの間に入るだけで検索に影響する。これらの新しいノードは線形検索しなければならないかもしれない (finger がまだ正確でない場合)。しかし膨大な数のノードがシステムに参加しない限り、2 つの古いノード間のノードの数は非常に少ない可能性が高いため、検索への影響は無視できる程度である。形式的には次のように述べることができる:
定理 6. \(N\) 個のノードを持つ安定したネットワークを使用し、最大 \(N\) 個の別のノードの集合が finger ポインターなしで (ただし後続者のポインタは正しい) ネットワークに参加する場合、検索には高い確率で \(O(\log N)\) 時間がかかる。
より一般的には、finger を調整するのにかかる時間がネットワークのサイズが 2 倍になるのにかかる時間よりも短い限り、検索は引き続き \(O(\log N)\) ホップを取るはずである。
 5.2 障害とレプリケーション
5.2 障害とレプリケーション
ノード \(n\) が故障すると \(n\) を finger テーブルに含むノードは \(n\) の後続者ノードを見つける必要がある。さらに、システムが最安定化している間は \(n\) の障害が進行中のクエリーを中断させてはならない。
最悪の場合でも \({\it find\_successor}\) は後続者のみを使用して進行できることから、障害回復の重要なステップは正しい後続者ポインタを維持することである。これを実現するために各 Chord ノードは Chord リング上の最も近い \(r\) 個の (\(r\) 番目の?) 後続者ノードの "後続者リスト" を保持している。通常の操作では Figure 7 を変更したバージョンの \({\it stabilize}\) ルーチンが後続者リストを保持する。ノード \(n\) が後続者ノードの故障に気づくと、後続者ノードリストの最初のライブエントリに置き換える。この時点で \(n\) は故障したノードが後続者ノードだったキーの通常の検索を新しい後続者ノードに向けることができる。時間の経過とともに \({\it stabilize}\) は障害が発生したノードを指す finger テーブルのエントリと後続者リストエントリを修正してゆく。
ノード障害が起きてから安定化が完了するまでの間に、他のノードは \({\it find\_successor}\) 検索の一部として故障したノードを介してリクエストの送信を試みる場合がある。理想上は、タイムアウト後に失敗にもかかわらず別の経路で検索を進めることができる。多くの場合これは可能である。必要なのは代替ノードのリストであり、これは故障したノードの前にある finger テーブルのエントリで簡単に見つけることができる。故障したノードの finger テーブルインデックスが非常に低い場合、後続者リストのノードも代替ノードとして使用できる。
技術文書は次の 2 つの定理を証明しており、後続者リストを使用すると安定化中でも検索が成功し効率的であることを示している [21]:
定理 7. 初期状態で安定しているネットワークで長さ \(r=O(\log N)\) の後続者リストを使用し、すべてのノードが確率 1/2 で失敗した場合、高い確率で \({\it find\_successor}\) はクエリーのキーに最も近いライブ後続者を返す。
定理 8. 初期状態で安定しているネットワークで長さ \(r=O(\log N)\) の後続者リストを使用し、すべてのノードが確率 1/2 で失敗した場合、失敗したネットワークで \({\it find\_successor}\) を実行するのに期待される時間は \(O(\log N)\) である。
これらの証明の背後にある直感的な考え方は簡単である。ノードの \(r\) 個の後続者ノードはすべて \(2^{-r}=1/N\) の確率で失敗するため、高い確率でノードが認識してその最も近いライブ後続者にメッセージを転送することができる。
後続者リストのメカニズムはより上位のレイヤーのソフトウェアがデータを複製するのにも役立つ。Chord を使用する典型的なアプリケーションは、キーに関連付けられたデータの複製を、キーに関連付けられた \(k\) 個のノードに保存してもよい。Chord ノードが \(r\) 個の後続者ノードを追跡しているという事実は、後続者が参入したり消えたりしたとき、つまりソフトウェアが新しいレプリカを伝達する必要がある時に上位レイヤーのソフトウェアに通知することができることを意味する。
 6. シミュレーションと実験結果
6. シミュレーションと実験結果
この章ではシミュレーションによって Chord プロトコルを評価する。シミュレータは Figure 4 の検索アルゴリズムと、Section 5 で説明した少し古いバージョンの安定化アルゴリズムを使用する。またインターネットホスト上で動作する Chord ベースの運用システムから予備的な実験結果についても報告する。
 6.1 プロトコルシミュレータ
6.1 プロトコルシミュレータ
Chord プロトコルは反復または再帰スタイルで実装することができる。検索を開始するノードがすべての通信を開始する: 反復スタイルでは検索を解決するノードがすべての通信を開始する。それは一連のノードに finger テーブルからの情報を要求し、そのたびに Chord リング状で目的の後継者ノードに近づく。再帰スタイルでは、各中間ノードは後続者ノードに到達するまで次のノードに要求を転送する。シミュレータはプロトコルを反復スタイルで実装している。
 6.2 Load Balance
6.2 Load Balance
 6.3 Path Length
6.3 Path Length
 6.4 Simultaneous Node Failures
6.4 Simultaneous Node Failures
 6.5 Lookups During Stabilization
6.5 Lookups During Stabilization
 6.6 実験結果
6.6 実験結果
この章ではインターネット上に展開された Chord プロトタイプ実装から取得したレイテンシ測定について説明する。Chord ノードはカリフォルニア、コロラド、マサチューセッツ、ニューヨーク、ノースカロライナ、およびペンシルバニアの米国 RON テストベッド [1] のサブセット 10 サイトにある。Chord ソフトウェアは Unix 上で動作し、SHA-1 暗号論的ハッシュ関数から取得した 160 ビットの鍵を使用し、ノード間の通信に TCP を使用している。Chord は反復方式で動作する。これらの Chord ノードは実験的な分散ファイルシステム [7] の一部だが、ここではシステムの Chord コンポーネントのみについて考える。
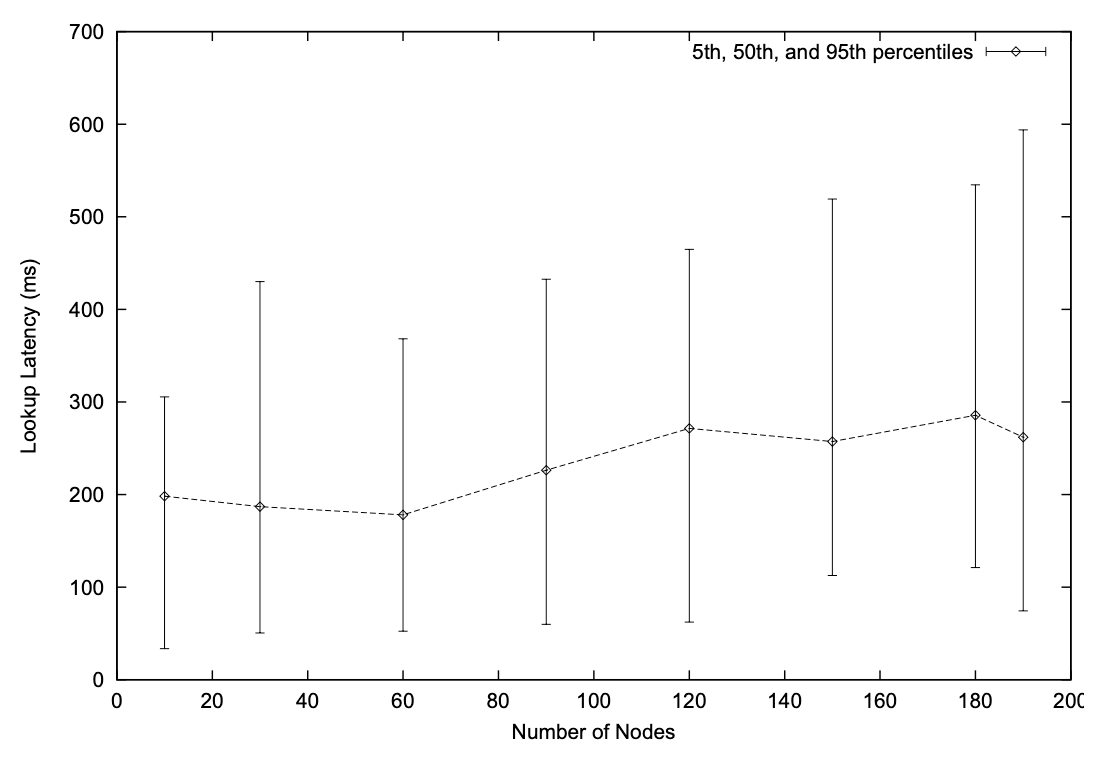
Figure 13 は様々なノード数での Chord 検索のレイテンシの測定結果を示している。各サイトで Chord ソフトウェアの複数の独立したコピーを実行することで 10 を超えるノード数での実験がおこなれている。これは、各サイトで \(O(\log N)\) の仮想ノードを実行して良好な負荷分散を提供するのとは異なるが、むしろ展開されているノード数が少ないにもかかわらず我々の実装がどれだけ適切にスケーリングできるかを測定することを目的としている。
Figure 13 に示すように、各物理サイトではランダムに選択されたキーに対して 1 つずつ 16 回の Chord 検索を発行している。グラフは検索レイテンシの中央値、5パーセンタイル、95パーセンタイルをプロットしている。レイテンシの中央値はノード数に応じて 180〜285 ミリ秒の範囲である。180 ノードのケースでは典型的な検索には 5 回の双方向メッセージ交換、つまり Chord 検索に 4、後続者ノードへの最後のメッセージに 1 が含まれている。サイト感の一般的な往復遅延は (ping により) 60 ミリ秒である。したがって 180 ノードの予測検索時間は約 300 ミリ秒であり、これは計測された中央値 285 に近い。5パーセンタイルのレイテンシが低いのは、クエリーノードに (ID 空間上) 近いキーの検索と、物理サイトのローカルにとどまるクエリーホップによるものである。95パーセンタイルが高いのは検索のホップが高い遅延の経路をたどるためである。
Figure 13 の教訓は、検索の遅延がノードの総数に応じてゆっくりと増加することであり、Chord のスケーラビリティを実証するシミュレーション結果を裏付けている。
 7. 今後の研究
7. 今後の研究
Section 6.6 で述べたプロトタイプでの経験に基づいて、我々は次の領域で Chord の設計を改善したいと考えている。
Chord には現在、分割されたリングを修復する特定のメカニズムがない; このようなリングは安定化手続きと局所的に一致して見えるかもしれない。グローバルな整合性を確認する 1 つの方法は、各ノード \(n\) が定期的に他のノードに \(n\) の Chord 検索を行うように依頼することである; 検索でノード \(n\) が見つけられない場合はパーティションがある可能性がある。これはノードが互いを知っているパーティションのみを検出するだろう。この知識を得る方法の一つは、すべてのノードが同じ小さな初期ノード集合を知ることである。別のアプローチは、ノードが過去に遭遇したランダムなノード集合の長期記憶を維持することである; パーティションが形成される場合、一方のパーティションのランダムセットにはもう一方のパーティションのノードが含まれている可能性がある。
悪意またはバグのある Chord 参加者の集合が Chord リングの不正なビューを提示する可能性がある。Chord が位置を特定するために使用しているデータが暗号論的に認証されていると仮定すると、これはデータの信頼性というより可用性に対する脅威となる。上記でパーティションを検出するのに使用したのと同じアプローチでは、被害者は Chord リングのグローバルに一貫したビューを見ていないことを被害者自身が認識するのに役立つ。
攻撃者は、項目のキーの直後の ID を持つノードを Chord リングに挿入し、データの取得を要求された時にエラーを返すことによって、特定のデータ項目を標的にすることができる。ノードが IP アドレスの SHA-1 ハッシュから派生した ID を使用することを要求 (および検証) することでこの攻撃は困難になる。
特にインターネット上のランダムなホストのそれぞれにメッセージを送信しなければいけない場合、検索あたり \(\log N\) のメッセージでも Chord の一部のアプリケーションには多すぎるかもしれない。Chord は 2 のべき乗の距離で finger を配置する代わりに \(1+1/d\) の整数倍の距離に配置するよう容易に変更することができる。このようなスキームでは 1 回のルーティングホップごとに距離を \(1/(1+d)\) に減少させることができるため \(\log_{1+d} N\) ホップで十分である。しかし必要な finger の数は \(N/(\log (1+1/d)) \approx O(d \log N)\) に増加するだろう。
検索のレイテンシを改善する別のアプローチはサーバ選択を使用することである。各 finger テーブルのエントリは ID リング上のそのエントリの間隔の最初の \(k\) 個のノードを指すことができ、ノードは \(k\) 個の各ノードへのネットワーク遅延を測定できる。通常 \(k\) 個のノードは検索の目的ではすべて同等であるため、ノードはレイテンシが最も小さいノードに検索を転送することができる。レイテンシを測定するノードが検索を転送するノードでもあるような再帰的な Chord 検索でこのアプローチは最も効果的である。
 8. 考察
8. 考察
多くの分散 P2P アプリケーションではデータ項目を格納するノードを決定する必要がある。Chord プロトコルは分散化された方法でこの困難な問題を解決する。キーが与えられると、そのキーの値を格納するノードを決定し効率的に実行する。定常状態では \(N\) ノードのネットワークでは各ノードは \(O(\log N)\) 個の他のノードについてのみルーティング情報を保持し、他のノードへの \(O(\log N)\) メッセージを介してすべての検索を解決する。ノードの離脱や参加によるルーティング情報の更新は \(O(\log^2 N)\) メッセージのみで済む。
Chord の魅力的な特徴は、そのシンプルさ、証明可能な正確さ、ノードの参加と離脱が同時に行われた場合でも証明可能な性質を持っていることである。ノードの情報が部分的に正しくない場合、Chord の性能は低下するものの正しく機能し続ける。我々の理論分析とシミュレーション、実験結果から、Chord はノード数に応じてスケーリングし、多数の同時ノード障害や参加から回復し、回復時にもほとんどの検索に正しく応答できることが確認されている。
協調的なファイル共有、時間共有型の可用性ストレージシステム、ドキュメントやサービス発見のための分散インデックス、大規模分散コンピューティングプラットフォームなど、P2P の大規模分散アプリケーションにおいて Chord は貴重なコンポーネントになると確信している。
 Acknowledgements
Acknowledgements
We thank Frank Dabek for the measurements of the Chord prototype described in Section 6.6, and David Andersen for setting up the testbed used in those measurements.
 参考文献
参考文献
- ANDERSEN, D. Resilient overlay networks. Master’s thesis, Department of EECS, MIT, May 2001. http://nms.lcs.mit.edu/projects/ron/.
- BAKKER, A., AMADE, E., BALLINTIJN, G., KUZ, I., VERKAIK, P., VAN DER WIJK, I., VAN STEEN, M., AND TANENBAUM., A. The Globe distribution network. In Proc. 2000 USENIX Annual Conf. (FREENIX Track) (San Diego, CA, June 2000), pp. 141–152.
- CHEN, Y., EDLER, J., GOLDBERG, A., GOTTLIEB, A., SOBTI, S., AND YIANILOS, P. A prototype implementation of archival intermemory. In Proceedings of the 4th ACM Conference on Digital libraries (Berkeley, CA, Aug. 1999), pp. 28–37.
- CLARKE, I. A distributed decentralised information storage and retrieval system. Master’s thesis, University of Edinburgh, 1999.
- CLARKE, I., SANDBERG, O., WILEY, B., AND HONG, T. W. Freenet: A distributed anonymous information storage and retrieval system. In Proceedings of the ICSI Workshop on Design Issues in Anonymity and Unobservability (Berkeley, California, June 2000). http://freenet.sourceforge.net.
- DABEK, F., BRUNSKILL, E., KAASHOEK, M. F., KARGER, D., MORRIS, R., STOICA, I., AND BALAKRISHNAN, H. Building peer-to-peer systems with Chord, a distributed location service. In Proceedings of the 8th IEEE Workshop on Hot Topics in Operating Systems (HotOS-VIII) (Elmau/Oberbayern, Germany, May 2001), pp. 71–76.
- DABEK, F., KAASHOEK, M. F., KARGER, D., MORRIS, R., AND STOICA, I. Wide-area cooperative storage with CFS. In Proceedings of the 18th ACM Symposium on Operating Systems Principles (SOSP’01) (To appear; Banff, Canada, Oct. 2001).
- DRUSCHEL, P., AND ROWSTRON, A. Past: Persistent and anonymous storage in a peer-to-peer networking environment. In Proceedings of the 8th IEEE Workshop on Hot Topics in Operating Systems (HotOS 2001) (Elmau/Oberbayern, Germany, May 2001), pp. 65–70.
- FIPS 180-1. Secure Hash Standard. U.S. Department of Commerce/NIST, National Technical Information Service, Springfield, VA, Apr. 1995.
- Gnutella. http://gnutella.wego.com/.
- KARGER, D., LEHMAN, E., LEIGHTON, F., LEVINE, M., LEWIN, D., AND PANIGRAHY, R. Consistent hashing and random trees: Distributed caching protocols for relieving hot spots on the World Wide Web. In Proceedings of the 29th Annual ACM Symposium on Theory of Computing (El Paso, TX, May 1997), pp. 654–663.
- KUBIATOWICZ, J., BINDEL, D., CHEN, Y., CZERWINSKI, S., EATON, P., GEELS, D., GUMMADI, R., RHEA, S., WEATHERSPOON, H., WEIMER, W., WELLS, C., AND ZHAO, B. OceanStore: An architecture for global-scale persistent storage. In Proceeedings of the Ninth international Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS 2000) (Boston, MA, November 2000), pp. 190–201.
- LEWIN, D. Consistent hashing and random trees: Algorithms for caching in distributed networks. Master’s thesis, Department of EECS, MIT, 1998. Available at the MIT Library, http://thesis.mit.edu/.
- LI, J., JANNOTTI, J., DE COUTO, D., KARGER, D., AND MORRIS, R. A scalable location service for geographic ad hoc routing. In Proceedings of the 6th ACM International Conference on Mobile Computing and Networking (Boston, Massachusetts, August 2000), pp. 120–130.
- MOCKAPETRIS, P., AND DUNLAP, K. J. Development of the Domain Name System. In Proc. ACM SIGCOMM (Stanford, CA, 1988), pp. 123–133.
- MOTWANI, R., AND RAGHAVAN, P. Randomized Algorithms. Cambridge University Press, New York, NY, 1995.
- Napster. http://www.napster.com/.
- Ohaha, Smart decentralized peer-to-peer sharing. http://www.ohaha.com/design.html.
- PLAXTON, C., RAJARAMAN, R., AND RICHA, A. Accessing nearby copies of replicated objects in a distributed environment. In Proceedings of the ACM SPAA (Newport, Rhode Island, June 1997), pp. 311–320.
- RATNASAMY, S., FRANCIS, P., HANDLEY, M., KARP, R., AND SHENKER, S. A scalable content-addressable network. In Proc. ACM SIGCOMM (San Diego, CA, August 2001).
- STOICA, I., MORRIS, R., KARGER, D., KAASHOEK, M. F., AND BALAKRISHNAN, H. Chord: A scalable peer-to-peer lookup service for internet applications. Tech. Rep. TR-819, MIT LCS, March 2001. http://www.pdos.lcs.mit.edu/chord/papers/.
- VAN STEEN, M., HAUCK, F., BALLINTIJN, G., AND TANENBAUM, A. Algorithmic design of the Globe wide-area location service. The Computer Journal 41, 5 (1998), 297–310.
翻訳抄
Consistent Hashing を使用した分散ハッシュテーブルアルゴリズム Chord に関する 2001 年の論文。2003 年に似た内容で新しい論文 [2] が出ているのでそちらを参照したほうが良いかも知れない。
- I. Stoica, R. Morris, D. Karger, M. F. Kaashoek, and H. Balakrishnan. Chord: A Scalable Peer-to-peer Lookup Service for Internet Applications. In Proc. ACM SIGCOMM’01, San Diego, CA, Aug. 2001.
- I. Stoica, R. Morris, D. Liben-Nowell, D.R. Karger, M.F. Kaashoek, F. Dabek, H. Balakrishnan. Chord: a scalable peer-to-peer lookup protocol for internet applications Feb. 2003 IEEE/ACM Trans. Netw17-32 11, 1