アルゴリズム
\(\def\vector#1{\boldsymbol{#1}}\)

分散ハッシュテーブル

Takami Torao #P2P #DHT #DOLR #Tapestry
  • このエントリーをはてなブックマークに追加

概要

分散データベースにおいて目的とするオブジェクトを効率的に検索するために特定のスキームに基づいてネットワークに配置する方法を分散オブジェクトロケーション/ルーティング (DOLR; decentralized object location and routing) と呼ぶ。一般的にはオブジェクト識別子をノードのアドレス空間にマッピングすることで行われる。分散ハッシュテーブル (DHT; distributed hashtable) はハッシュ関数を使用して識別子 (キー) に関連付けられたオブジェクト (値) を格納および取得できる DOLR の一つである。

ある識別子に対して複数のノードでオブジェクトがコピーされるとき、分散ハッシュテーブルは冗長化されている。またテーブルやツリーのような構造を持つオブジェクトを独立した複数の部分に分割してそれぞれ異なる識別子で分散保存する方法をシャーディング (sharding) と呼ぶ。

Table of Contents

  1. 概要
  2. ルーティングアルゴリズム
    1. Plaxton ルーティング
    2. \(n\) 分木ルーティング
    3. 対数メッシュリング
  3. 内部状態
    1. 定数次数グラフ
  4. 分散ハッシュテーブル実装
    1. Pastry
    2. Bamboo
    3. Z リング
    4. CAN
    5. P-Grid
  5. 参考文献

分散ハッシュテーブルのアルゴリズムの比較は以下の観点に注目する。

オブジェクトロケーション
あるオブジェクトの担当となるノードをどのように決定するか。これはネットワーク上にオブジェクトがどのように配置されるかにも関係する。例えば Consistent Hashing のようにオブジェクトの内容に依存しない方法で一様に配置させることで負荷を分散させる構成を選択することもあれば、負荷の偏りを許容する代わりにレンジクエリー (範囲指定の検索) の効率を優先することもある。
ルーティング
あるノードから目的とするノードまでどのような経路を選択するか。これは分散ハッシュテーブル上でオブジェクトを検索するときのパフォーマンスに影響し、また一部のノードがクラッシュしたときに代替経路を選択できるかを評価する。一般にルーティングコストを下げるには一つのノードから多くの他のノードを参照する必要がありあり、内部状態のサイズ増加につながることから、それらは非独立な関係である。
内部状態
分散ハッシュテーブル機能を維持するためにそれぞれのノードが維持しなければならない内部状態 (ルーティングテーブル) の大きさ。これは他のノードへのリンク数 (グラフ理論の観点では出次数) を意味している。一般に、定数次数 \(O(1)\) を持つ構造のルーティングコストは \(O(N)\) の増加、対数次数 \(O(\log N)\) 構造のルーティングコストは \(O(\log N)\) の増加、完全グラフのようにすべてのノードが参照関係を持つ \(O(N)\) 構造のルーティングは \(O(1)\) の増加となる。
メンテナンス
分散ハッシュテーブルに新規ノードが参加したり既存のノードが離脱するときの動作。とりわけ、非同期環境でそれらが同時に進行しても安全であることが証明されているかは重要である (安全とは、最終的に正しい構造に落ち着き、多少の遅延があるとしても伝達中のメッセージが最終的に目的地に到着することを意味する)。一般にノードの被参照数が多い構造、つまり大きな内部状態となる構造は他の多くのノードのルーティングテーブルを書き換えなければならないことから参加/離脱が起きたときのパフォーマンスは落ちる。

ルーティングアルゴリズム

目的のノードに到達するまでのホップ数を削減しようとすれば、各ノードの持つ内部状態 (ルーティングテーブル) が大きくなり、新規ノードの参加や離脱が起きたときのメンテナンスコストが大きくなる。レンジクエリー (キーの範囲を指定したクエリー) が可能な構造は負荷が分散できないことを意味している。

Plaxton ルーティング

Plaxton ルーティング (PRR ルーティング) は Plaxton, Rajaraman および Richa (PRR) が 1997 年に発表した論文 [1] に基づくルーティングアルゴリズムである。これは分散システムでの DOLR に関する最初のアルゴリズムであり後の DHT 設計の基礎となった。

オブジェクト識別子に対して前方一致または末尾一致に基づいて階層的に目的のノードを探索する方法をそれぞれ Prefix ルーティング、Suffix ルーティングと呼ぶ。Plaxton ルーティングは Fig 1 に示すようなルーティングテーブルを作成するタイプの Suffix ルーティングである。

Fig 1 の例では 16 ビットのオブジェクト識別子の 4 ビットごとに一致する 3 レベル (階層) の Suffix ルーティングの単純化したモデルを示している。例えば識別子 0x7E5A のオブジェクトは *E5A を担当するノードに格納される。

Fig 1. 4 ビットごとに一致する 3 レベルの 16 ビット識別子を使った Suffix ルーティングテーブル。識別子が単調増加する数値の場合、Prefix ルーティングでは特定のエントリに負荷が偏るが Suffix ルーティングでは均等に分散する。

PRR 論文は静的なネットワークを前提としていて、ネットワークに保存されているオブジェクトの読み込み、追加、削除操作が可能である。各ノードは、固定個数のレベルと各レベルごとに固定個数のエントリで構成されたルーティングテーブルが存在する。ノード間にはコスト値が定義されており、最も低いコスト値を持つノードは Primary Neighbor となる。また特定のコスト基準を満たすノードが存在するのであればそれは Secondary Neighbor となる。レベル間の接続は下層の Primary Neighbor (プライマリリンク) と Secondary Neighbor (セカンダリリンク) の経路で保存される。セカンダリリンクはプライマリリンクに障害が発生した場合に代替経路となる。プライマリリンクで関連付けられた先のノードには Reverse リンクによる逆参照が存在する。

Plaxton ルーティングは \(n\) 分木 (トライ木) 構造に抽象化されるため目的のノードに \(O(\log N)\) ホップで到達することができる。また近い Prefix を担当するノードは比較的近い距離でリンクされていることから探索木の部分木をトラバースする経路でレンジクエリー (キーの範囲指定クエリー) が可能であることも多い。

Pastry, Tapestry などは Plaxton ルーティングに基づく分散ハッシュテーブルである。

\(n\) 分木ルーティング

n 分木ルーティングは \(n\) 分木に基づいてノードを特定するルーティングの設計手法である。Plaxton ルーティングで 16 進数を 1 桁としたとき \(n=16\) 分木 (トライ木) ルーティングと考えることができる。P-Grid は 2 分木ルーティングに基づく分散ハッシュテーブルである。

対数メッシュリング

対数メッシュを持つリングは、閉じた数直線状の識別子空間 (リング) のそれぞれのノードに対数の Skip List を追加した構造である。グラフとしてみたとき、各ノードは \(\log N\) の次数を持つ。Chord, DKS(N,k,f), Chord# といった Consistent Hashing に基づく分散ハッシュテーブルの構造である。

内部状態

定数次数グラフ

Prefix ルーティングや対数メッシュリングの分散ハッシュテーブルをグラフとして見たとき、各ノードは対数次数 \(\log N\) で他のノードと接続している。これに対して de Bruijn グラフ、butterfly グラフ、超立方体環 (CCC; cube-connected cycles) といった構造を使用する分散ハッシュテーブルでは、ノードの次数はネットワークのサイズ \(N\) に依存しない定数値とすることができる。

次数が一定とは各ノードのルーティングテーブル (内部状態) のサイズがネットワークのサイズ \(N\) によらず一定であることを意味する。これは言い換えるとネットワークの増大によってルーティング経路が長くなることを意味している。定数次数の分散ハッシュテーブルではルーティング経路の増加オーダーがどれほどかが論点となる。

Koorde (de Bruijn graph), Ulysses (butterfly graph), Cycloid (CCC) などの分散ハッシュテーブルが存在する。

分散ハッシュテーブル実装

Tapestry

Tapestry(2,3) は PRR の論文(1)に基づいた Prefix ルーティングを行う分散ハッシュテーブルルゴリズム。RPP にノードの参加と離脱のアルゴリズムが追加されている。各ノードは SHA-1 を使用した ID (アドレス) が割り当てられ、アプリケーションにもエンドポイント GUID が割り当てられる。…

2020年8月12日(Wed) #DHT #Tapestry

Chord

Chord はコンシステントハッシュ法 (consistent hashing) に基づく分散ハッシュテーブルである。対数メッシュのリンクを内包する論理リングで表される。

2020年8月27日(Thu) #P2P #DHT #Chord

Kademlia

Kademlia は二分木構造に基づくシンプルで実用的な分散ハッシュテーブル (DHT; distributed hashtable) アルゴリズム。ネットワークの中から目的のノードを効率よく検索することのできる分散オブジェクトロケーション/ルーティング (DOLR; decentralized object location and routing) の一つである。…

2020年8月30日(Sun) #P2P #DHT #Kademlia

Pastry

Pastry[5] Prefix ルーティング。セカンダリリンクやリバースポインタはない。

Bamboo

結合と隣接ノードの管理方法が異なる Pastry に似た構造の Prefix ルーティング。

Z リング

各レベルには Pastry の Prefix ルーティングを使用するが、それらの間に完全なルーティングを持つ。\(\beta=4096\) と遥かに大きい基数を使用することで、ルーティングテーブルのサイズは大きくなる代わりにホップ数が減少する。3 レベルのアドレススペースを使用する。

CAN

CAN (content addressing network) は \(d\) 次元直交座標系にノードを配置し、その幾何学的経路によるルーティングを行う分散ハッシュテーブル。各ノードは座標系の上に領域が割り当てられ、それぞれのノードは隣接する領域のノードのみしか参照しないため定数次数のグラフとみなすことができる。

Fig 2 左図は 2 次元空間に配置した 5 つのノードを表している。矩形の領域がそのノードの担当するオブジェクト識別子の範囲に相当する。

CAN のルーティングは隣接ノードの中から宛先のノードにもっとも近いノードに転送することによって行われる (greedy forwarding)。Fig 2 左図で E が隣接しているのは C, D, B である。ここで E の右隣りは循環して C とつながる点に注意 (つまりトーラスの構造を持つ空間である; 同様に E の上隣りは B である)。Fig 2 右図はノード x から y へのルーティングを示している。この方法はいくつかの経路が考えられ、経路 1 は 6 ホップ、経路 2 は 7 ホップ、経路 3 は 5 ホップと結果的なホップ数は異なるものの、いずれの経路でも y に到達する。

最短経路を求めないのであれば目的のノードへの代替経路は多数存在する。このような経路の冗長性により、宛先にもっとも近い隣接ノードがクラッシュしていたとしても、それ以外の隣接ノードへ転送することで (効率は落ちるかもしれないが) 結果的に目的のノードへ到達することができる。

Fig 2.

\(n\) 個のノードがすべて等しい区画に割り当てられた \(d\) 次元空間では平均のルーティング経路長は \((d/4)(n^{1/d})\) となる。またそれぞれのノードは \(2d\) の隣接ノードへの参照を維持する。CAN はノードの内部状態を増加させることなくノード数 \(n\) を増やすことができるが、平均のルーティング経路長は \(O(n^{1/d})\) で増加する。

CAN は \(d\) 次元のトーラス構造を持つことから、Chord のような閉じた 1 次元片方向リンク構造を \(n\) 次元両方向リンク構造に拡張した構造とも見ることができる。ただし、Chord や DKS が探索効率化のために対数メッシュ (skip list) を導入したのに対して、CAN ではそのような構造は導入せず、あくまで隣接ノードのみへの転送にとどめることで内部状態を定数化したという違いがある。

P-Grid

P-Grid (peer-grid) [4] は 2 進数で表されるオブジェクト識別子に対して Prefix ルーティングを行う分散ハッシュテーブルアルゴリズム。Tapestry と異なりノードの識別子 (アドレス) とオブジェクトの識別子は関連していない。オブジェクト識別子はネットワークの規模に拘らず任意のサイズを使用することができる。

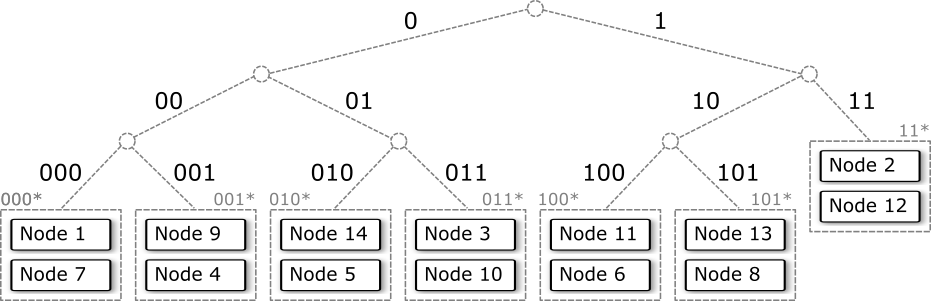
ノードは Fig 3 に表すような平衡二分探索木の構造でオブジェクト識別子に対応するノードを割り当てる。この二分木の葉に 2 つ以上のノードを割り当てることでオブジェクトのレプリケーションを行う。

Fig 3. Node 1 から 14 までのノードで構成した P-Grid ネットワーク。Prefix を担当する葉のそれぞれに 2 つのノードが割り当てられている。

それぞれのノードが持つルーティングテーブルは、二分木の根からそのノードに到達するまでに分岐した枝の Prefix と、それら枝の先に存在するノードを (経路を多重化する場合は複数) マッピングしている。葉として多重化されているノードは同じノードへのリンクでもよい。

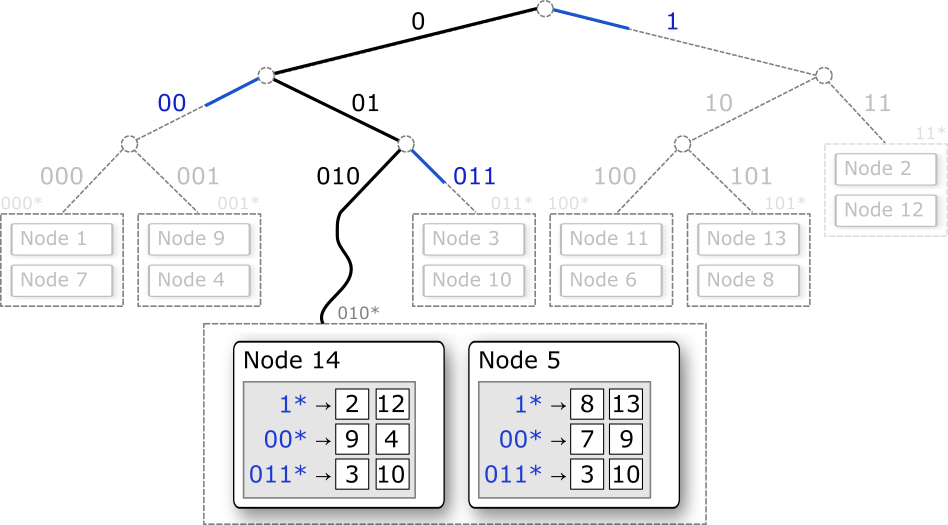
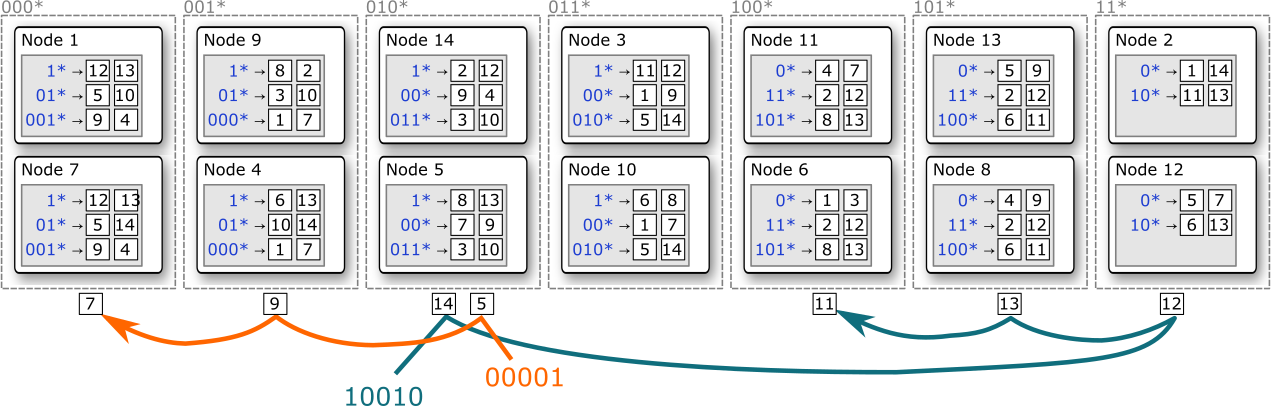
Fig 4. Prefix 010* を担当するノード 14 と 5 の持つルーティングテーブル。それぞれのノードには二重化した転送経路が設定されている。

メッセージは P-Grid ネットワークに参加している任意のノードから開始することができる。メッセージを受信したノードは宛先の識別子が自分の担当する Prefix を持つのであれば自分 (そして同じ Prefix を担当する他のノード) 宛であることが分かる。メッセージが自分宛てでない場合、ローカルのルーティングテーブルから転送先のノードを選んでメッセージを転送する。

Fig 5. P-Grid でのメッセージの転送例。

P-Grid の論文[4]では動的なノードの参加と離脱は言及されていない。そのような操作は二分木全体の構造を一時的に把握する必要があるだろう。ただし、枝の細分化や統合が行われるだけであるためすべてのノードのルーティングテーブルを更新する必要はない。

参考文献

  1. Plaxton CG, Rajaraman R, Richa A. Accessing nearby copies of replicated objects in a distributed environment. In Anon, editor, Annual ACM Symposium on Parallel Algorithms and Architectures. New York, NY, United States: ACM. 1997. p. 311-320
  2. Ben Y. Zhao, John Kubiatowicz, Anthony. D. Joseph. Tapestry: An infrastructure for fault-tolerant wide-area location and routing. Univ. California, Berkeley, CA, Tech. Rep. CSD-01-1141, Apr. 2001.
  3. Ben Y. Zhao, Ling Huang, Jeremy Stribling, Sean C. Rhea, Anthony D. Joseph, John D. Kubiatowicz. Tapestry: A Resilient Global-Scale Overlay for Service Deployment. IEEE Journal on Selected Areas in Communications. 22 (1): 41–53.
  4. Anwitaman Datta, M. Hauswirth, R. John, R. Schmidt and K. Aberer. Range queries in trie-structured overlays, Fifth IEEE International Conference on Peer-to-Peer Computing (P2P'05), Konstanz, 2005, pp. 57-66, doi: 10.1109/P2P.2005.31.
  5. A. Rowstron, P. Druschel. Pastry: Scalable, decentralized object location and routing for large-scale peer-to-peer systems, Proceedings of the IFIP/ACM International Conference on Distributed Systems Platforms, Heidelberg Nov 12–16, 2001329-350
  6. I. Stoica, R. Morris, D. Karger, M. Kaashoek, H. Balakrishnan. Chord: A scalable peer-to-peer lookup service for Internet applications, 2001 ACM SIGCOMM 2001 San Diego, CA149-160