Kademlia
 概要
概要
Kademlia は二分木構造に基づくシンプルで実用的な分散ハッシュテーブル (DHT; distributed hashtable) アルゴリズム。ネットワークの中から目的のノードを効率よく検索することのできる分散オブジェクトロケーション/ルーティング (DOLR; decentralized object location and routing) の一つである。Kademlia は、P2P のような大規模ネットワークにおいて長期間安定して駆動しているノードを優先的にキャッシュするルーティングテーブルの構築アルゴリズムを示している。
Kademlia のアプローチはノード ID のビットの先頭から二分木 (トライ木![]() ) を構築する (接頭辞で区分けする点では Tapestry と似ている)。Kademlia は構造のシンプルさや \(O(\log N)\) でのノード検索といった一般的な分散ハッシュテーブルの特徴に加えて、より効率的なルーティング経路の選択と冗長化、並列化可能なノード検索、Churn 耐性、そして Gnutella の実行統計から得られた成果として長期間駆動しやすいノードの参照を選択的に残す方法など、より現実的な機能を備えている。これらの特徴は Kademlia の \(k\)-バケット (\(k\)-bucket) というルーティングテーブルの構造と XOR 距離という指標によってもたらされている。
) を構築する (接頭辞で区分けする点では Tapestry と似ている)。Kademlia は構造のシンプルさや \(O(\log N)\) でのノード検索といった一般的な分散ハッシュテーブルの特徴に加えて、より効率的なルーティング経路の選択と冗長化、並列化可能なノード検索、Churn 耐性、そして Gnutella の実行統計から得られた成果として長期間駆動しやすいノードの参照を選択的に残す方法など、より現実的な機能を備えている。これらの特徴は Kademlia の \(k\)-バケット (\(k\)-bucket) というルーティングテーブルの構造と XOR 距離という指標によってもたらされている。
P2P ファイル共有では Gnutella, BitTorrent, IPFS で使用されている。またブロックチェーンでの PoC として Ethereum 1 や Storj, Dfinity などのノード検索で検討されている。
Table of Contents
 アルゴリズム構造
アルゴリズム構造
Kademlia では検索キーに最も近い ID を持つノードをそのキーに対応するノードとしている。"対応" が意味するところはアプリケーションに依存する。例えば KVS であれば key-value の保存と参照の責務を持つノードとなるだろう。Kademlia の論文 [1] では KVS の実装として紹介しているが、キーに対応するノードを特定した後にシステムがどのように動作するかについて設計上の制約はない。
検索キーとノード ID は同じサイズのデータである。[1] ではともに 160-bit の空間としている (この 160-bit は任意長のキーを SHA-1 でハッシュ化することを意図してるだけで、アルゴリズムの設計としてキーのサイズに制限はない)。
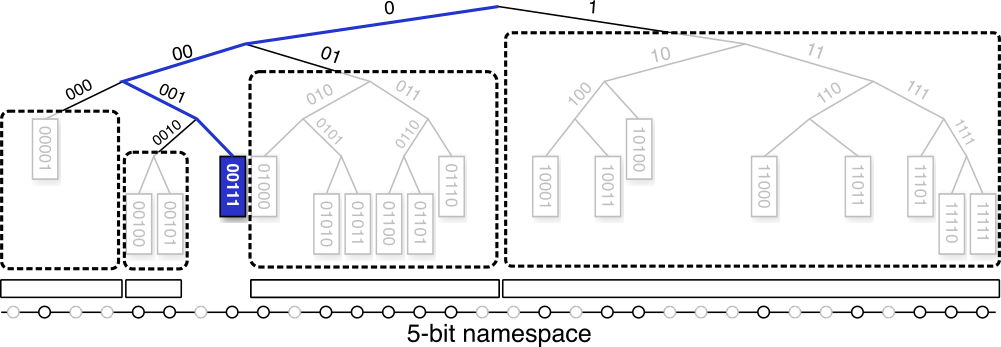
Kademlia ネットワークのノードは Fig 1 に示すように各ノード ID の 2 進数表現に基づいて概念上の二分木構造に配置される。
ノード ID に偏りがあるとキーレンジの広いノードに負荷が集中し Kademlia ネットワーク全体の性能が低下する。したがってノード ID も検索キーも一様にランダムに分布するように設計する必要がある。
 ルーティングテーブル
ルーティングテーブル
Kademlia の各ノードはそれぞれ独自のルーティングテーブルを持っている。ルーティングテーブルは二分木の根から自身のノード ID までを結ぶ経路 (Fig 2 の青いライン) から分岐した部分木に含まれるノードを最大 \(k\) 個保持する。この各部分技に対応する順序付けされた最大 \(k\) 個の列を \(k\)-バケットと呼ぶ。
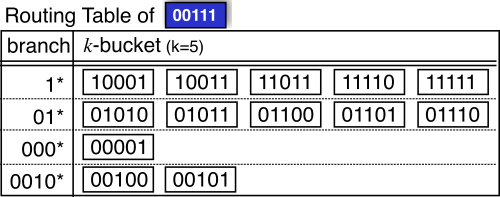
00111 のルーティングテーブルの例。\(k\)-バケットは二分木の根と 00111 を結ぶ経路から分岐した先に存在する最大 \(k\) 個のノードを参照する。最上位の部分木は二分木を 2 分割した空間のうち自身のノードが含まれていない方である。二層目の部分技はさらに 2 分割したうちの自身のノードが含まれていない方である。\(k\)-バケットはこのような二分木の 2 分割を繰り返した範囲それぞれに含まれているノードの参照を表している。
\(k\)-バケットにはメッセージのやりとりの中で自身のノードが「発見」したノードが追加されてゆく (つまり \(k\)-バケットが空であれば、その部分木の空間にまだ 1 つもノードを見つけていないことを意味している)。Kademlia のプロトコルには明示的なノードの参加や離脱の通知が存在しない代わりに、各ノードはメッセージを中継するときにそのメッセージに含まれる送信者ノードを「発見」し、必要に応じてその ID とアドレスで対応する \(k\)-バケットを更新する。
Kademlia ネットワーク開始時の最初のノードはすべての名前空間を範囲とする一つの \(k\)-バケットのみを持っている。ノード A がノード B から発信されたメッセージを受信したとき、ノード B に対応する \(k\)-バケットに B が含まれているかを確認する。対応する \(k\)-バケットにノード B が:
- 含まれている場合、ノード B をバケットの末尾に移動する。
- 含まれていない場合、バケットのノード数が:
- \(k\) 個より少なければ単純にその末尾にノード B を追加する。
- \(k\) 個の場合、その \(k\)-バケットの範囲に自身のノード ID が:
- 含まれる場合、\(k\)-バケットを二分割し、すでに存在する \(k\) 個のノードをそれぞれの \(k\)-バケットへ分配する。その後にノード B に対応する方の \(k\)-バケットにノード B の追加を再帰的に試行する。
- 含まれない場合、\(k\)-バケットのノード交換用キャッシュに保存する。後の動作で応答しないノードが発生したとき、この交換用キャッシュのもっとも最近に追加されたノードと疎通確認を行い、正しい応答があれば応答しなくなったノードと置き換える。
以上の動作で Kademlia のルーティングテーブルはトラフィックによって最新の状態に保たれる構造をしている。一定時間 (論文では 1 時間) ノード検索が行われていない \(k\)-バケットは、そのバケットに含まれるノードをランダムに選択し検索を行うことで強制的にリフレッシュする。結果的に \(k\)-バケットには長期間正常に駆動しているノードが優先して残る構造になっており、もっとも最近に疎通が確認されたノードがバケットの末尾に配置されている。
いっぱいになった \(k\)-バケットでノードの入れ替えが発生するのは、既存のノードのいずれかの疎通確認が失敗したときのみであることに注意。これは、一度に大量のノードを参加させ特定の範囲の \(k\)-バケットのルーティングを支配するような DoS 攻撃への耐性を示している (Churn 耐性)。
 XOR 距離関数
XOR 距離関数
Kademlia は検索キーに最も近い ID を持つノードがそのキーを「担当」する。例えば KVS であれば、key-value ペアはキーとの距離がもっとも近い ID を持つノードに保存される。Kademlia でのノード ID とキーとの距離関数はそれらのビット単位での XOR (排他的論理和) と定義されている。例えばノード 3 (b011) とノード 5 (b101) が存在するとき、それぞれからキー 1 (b001) に対する距離は: \[ \left\{ \begin{array}{lcl} {\tt 011} \oplus {\tt 001} & = & {\tt 010} \ \ \mbox{(2 in decimal)}\\ {\tt 101} \oplus {\tt 001} & = & {\tt 100} \ \ \mbox{(4 in decimal)} \end{array} \right. \] となることから、キー 1 はノード 5 よりもノード 3 のほうが近いと考えることができる。
距離関数に XOR を使用する利点はトポロジーの距離の捉え方が単純になることである。ノード ID やキーを点 \(x, y\) としたとき、その距離が関数 \(d(x,y)\) で表されるとすると、XOR による距離は以下の特徴を持つ。
- \(d(x, x)=0\), 例えば \(d({\tt 011},{\tt 011})=0\)
- \(x \ne y\) のとき \(d(x,y)\gt 0\)
- すべての \(x,y\) に対して \(d(x,y)=d(y,x)\)
- \(d(x,z) \le d(x,y) + d(y,z)\)、すなはち \(x\) と \(z\) の直線距離 \(d(x,z)\) よりも \(x\)-\(z\) 距離が短くなるような中継点 \(y\) は存在しない
Chord のようにある範囲での剰余による循環値 \(i \bmod 2^x\) (剰余環) を使う方法は、順方向と逆方向の 2 つのトポロジーが同時に存在し双方で距離の捉え方が異なる。時計盤に例えると、4 時から 6 時までの距離は 2 時間だが、同じトポロジーでの 6 時から 4 時までの距離は 10 時間となる。これらを同じ距離とするなら状況に応じてトポロジーを変換しなければならない複雑さをもたらしている。このため Chord は順方向のトポロジーしか考慮しておらず、点 \(x\) からもっとも遠い点はその直前の点 \((x - 1) \bmod n\) である。
一方、XOR 距離関数では 2 つの点 \(x\) と \(y\) は特徴 3 より可換である。つまり \(x\) と \(y\) のどちらを基準にしても他方への距離は同じである。これは Kademlia のトポロジーが単一方向性 (unidirectional) であることを示している。
特徴 4 は、\(x\) のルーティングテーブルの中で \(z\) にもっとも近いノードを選択したときに \(x\)-\(z\) 間の距離より近くなるような距離を持つ \(x\)-\(y\)-\(z\) 経路は存在しないことを意味している。これはつまり \(x\)-\(z\) を直接結ぶよりも距離が短くなるような経路は存在しないというユークリッド空間上の特徴と等しい。この特徴により、\(z\) により近いノードへの移動することで \(z\) までの距離は必ず縮まること、それを繰り返すことでどのような経路であっても最終的に \(z\) にもっとも近いノードに収束することを示している。実際、2 点 \(x\), \(y\) からある点 \(z\) へ向かう探索はどちらも同じ経路に収束する傾向を持つ。
| XOR | 0 (b000) | 1 (b001) | 2 (b010) | 3 (b011) | 4 (b100) | 5 (b101) | 6 (b110) | 7 (b111) |
|---|---|---|---|---|---|---|---|---|
| 0 (b000) | 0 (b000) | 1 (b001) | 2 (b010) | 3 (b011) | 4 (b100) | 5 (b101) | 6 (b110) | 7 (b111) |
| 1 (b001) | 1 (b001) | 0 (b000) | 3 (b011) | 2 (b010) | 5 (b101) | 4 (b100) | 7 (b111) | 6 (b110) |
| 2 (b010) | 2 (b010) | 3 (b011) | 0 (b000) | 1 (b001) | 6 (b110) | 7 (b111) | 4 (b100) | 5 (b101) |
| 3 (b011) | 3 (b011) | 2 (b010) | 1 (b001) | 0 (b000) | 7 (b111) | 6 (b110) | 5 (b101) | 4 (b100) |
| 4 (b100) | 4 (b100) | 5 (b101) | 6 (b110) | 7 (b111) | 0 (b000) | 1 (b001) | 2 (b010) | 3 (b011) |
| 5 (b101) | 5 (b101) | 4 (b100) | 7 (b111) | 6 (b110) | 1 (b001) | 0 (b000) | 3 (b011) | 2 (b010) |
| 6 (b110) | 6 (b110) | 7 (b111) | 4 (b100) | 5 (b101) | 2 (b010) | 3 (b011) | 0 (b000) | 1 (b001) |
| 7 (b111) | 7 (b111) | 6 (b110) | 5 (b101) | 4 (b100) | 3 (b011) | 2 (b010) | 1 (b001) | 0 (b000) |
 プロトコル
プロトコル
Kademlia の論文で紹介している RPC は以下の 4 つである。ただし STORE と FIND_VALUE は参照実装的な KVS を実装するための機能であるため、ルーティングとしての機能は PING と FIND_NODE で充足している。
def PING(contact:Contact)def FIND_NODE(key:ID): List[Contact]def STORE(key:ID, value:Array[Byte])def FIND_VALUE(key:ID): Array[Byte]
 参考文献
参考文献
- Maymounkov P., Mazières D. Kademlia: A Peer-to-Peer Information System Based on the XOR Metric (日本語訳). In: Druschel P., Kaashoek F., Rowstron A. (eds) Peer-to-Peer Systems. IPTPS 2002. Lecture Notes in Computer Science, vol 2429. Springer, Berlin, Heidelberg.
- Xing Shi Cai, Luc Devroye. The Analysis of Kademlia for random IDs
- Distributed Hash Tables with Kademlia, Stanford Code the Change Guides