論文翻訳: Kademlia: A Peer-to-peer Information System Based on the XOR Metric

Abstract

障害の発生しやすい環境において証明可能な一貫性とパフォーマンスをもつ P2P システムについて述べる。我々のシステムはアルゴリズムを簡素化し、証明を用意にする新しい XOR ベースのメトリックストポロジーを用いてクエリーをルーティングし、ノードを探索する。このトポロジーには、交換されるすべてのメッセージが有用なコンタクト情報を伝える、または強化するという性質を持っている。このシステムはこの情報を利用してユーザにされるすべてのメッセージが有用なコンタクト情報を伝える、または強化するという性質を持っている。このシステムはこの情報を利用してユーザにタイムアウトの遅延を課すことなく、ノードの障害を許容する並列非同期のクエリーメッセージを送信する。

Table of Contents

1. Abstract
2. 1 導入
3. 2 システム詳細
   1. 2.1 XOR メトリクス
   2. 2.2 ノード状態
   3. 2.3 Kademlia プロトコル
   4. 2.4 ルーティングテーブル
   5. 2.5 効率的なキーの再発行
4. 3 証明の概略図
5. 4 実装ノート
   1. 4.1 最適化されたコンタクトアカウント
   2. 4.2 高速化された検索
6. 5 まとめ
7. References
8. 翻訳抄

1 導入

この論文では P2P 分散ハッシュテーブル (DHT) である Kademlia について述べる。Kademlia はこれまでの DHT では同時に提供されていなかった多くの望ましい機能を持っている。Kademlia はノードがお互いを知るために送信しなければならない設定メッセージ数を最小限に抑えている。設定情報はキー検索の副作用として自動的に拡散される。ノードは十分な情報と柔軟性を持ち、低レイテンシーの経路を介してクエリーをルーティングすることができる。Kademlia は故障したノードによるタイムアウトの遅延を回避するために並列の非同期クエリーを使用している。ノードが互いの存在を記録するアルゴリズムは、ある基本的なサービス拒否攻撃の耐性を持っている。最後に、Kademlia のいくつかの重要な特性は、駆動時間の分布に関する弱い仮定 (既存の P2P システムの測定値を用いて検証した仮定) を使用して形式的に証明することができる。

Kademlia は多くの DHT の基本的なアプローチを採用している。キーは不透明 (opaque; 検索に使用する以外に設計上の意味を持たない) な 160 ビット量である (例えばある大きなデータの SHA-1 ハッシュ値など)。参加するコンピュータは 160 ビットのキー空間にノード ID を持っている。〈key, value〉のペアは、ある近さの概念に対してキーに "近い" ID を持つノードに格納される。最後に、ノード ID に基づくルーティングアルゴリズムによって誰もが特定のターゲットキーに近いサーバを効率的に見つけることができる。

Kademlia の利点の多くはキー空間内のポイント間の距離に XOR メトリクスを使用していることである。XOR は対称的であるため、Kademlia の参加者はルーティングテーブルに含まれているノードの全く同じ分布から検索クエリーを受け取ることができる。この特性がないと Chord [5] などのシステムは受信したクエリーから有用なルーティング情報を学習することができない。さらに悪いことに、非対称性は硬直したルーティングテーブルにつながる。Chord ノードの finger テーブルの各エントリは ID 空間内のある区間の前にある正確なノードを格納しなければならない。区間内のノードは実際には同じ区間内で先行するノードから離れすぎているだろう。Kademlia はこれとは対照的に区間内の任意のノードにクエリーを送信することができ、レイテンシーに基づいてルートを選択したり、同等に適切な複数のノードに並列で非同期クエリーを送信することができる。

Kademlia は特定の ID に近いノードを探索するために最初から最後まで単一のルーティングアルゴリズムを使用する。これとは対照的に、他のシステムでは目標の ID に近づくためにあるアルゴリズムを使用し、最後の数ホップで別のアルゴリズムを使用している。既存のシステムの中で Kademlia がもっとも似ているのは Pastry [1] の第一フェーズ (この著者らはそのように表現していないが) であり、Kademlia の XOR メトリクスを用いてターゲット ID からほぼ半分の距離にあるノードを連続的に見つけるというものである。ただし、Pastry の第二フェーズでは距離メトリクスを ID 間の数値差に切り替える。またレプリケーションでは第二フェーズの数値差メトリクスを使用する。残念ながら、第二フェーズのメトリクスと近いノードは第一フェーズのメトリクスとかなり離れている可能性があり、特定のノード ID 値で不連続性が発生し、パフォーマンスが低下し、最悪ケースの挙動を形式的に分析する試みが複雑となる。

2 システム詳細

我々のシステムは他の DHT と同じ一般的なアプローチを採用している。160 ビットの不透明な ID をノードに割り当て、任意の目的 ID に "近い" ノードを連続的に検索し、対数的なステップで検索対象に収束させる検索アルゴリズムを提供する。

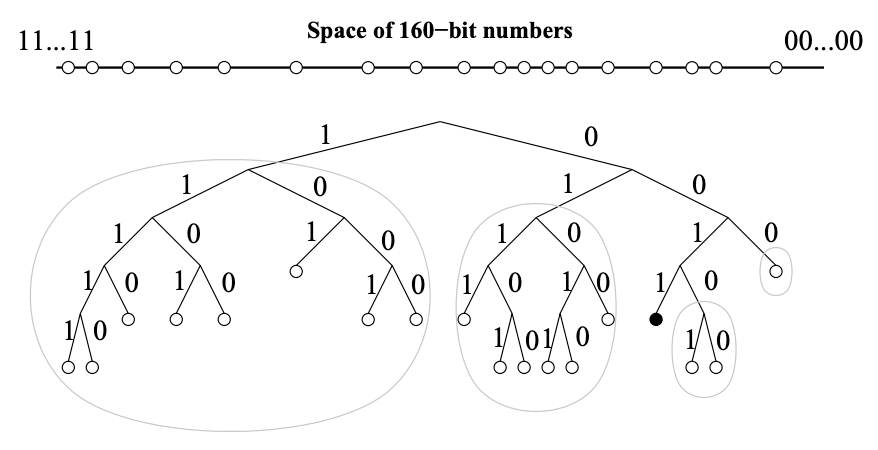
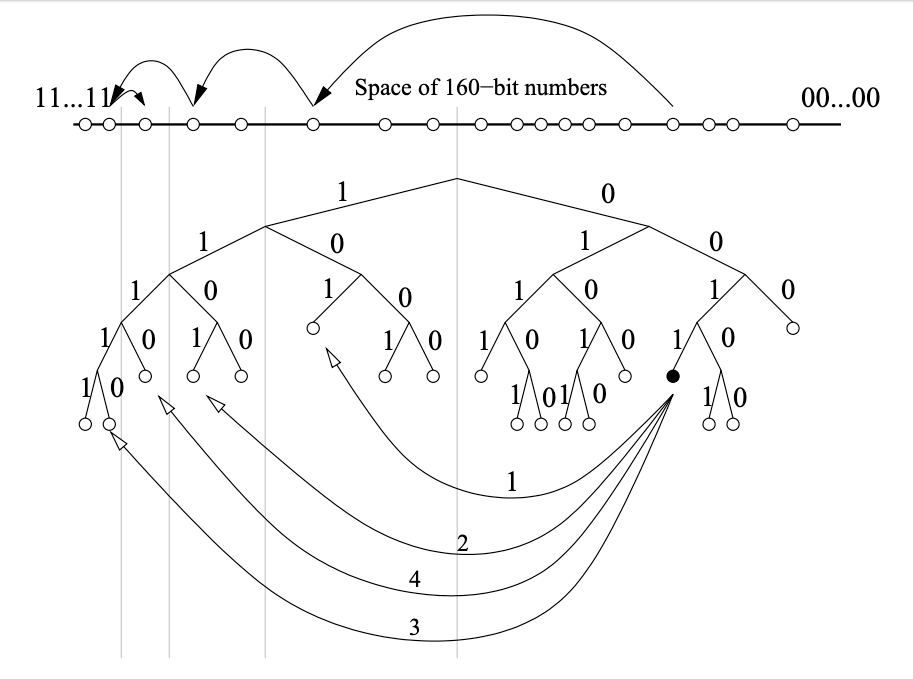
Kademlia はノードを二分木の葉のように効率的に扱い、各ノードの位置はその ID のもっとも近い一意のプレフィクスによって決定される。Fig. 1 はツリーの例として一意なプレフィクス 0011 を持つノードの位置を示している。この二分木はあるノードに対してそのノードを含まない下位のサブツリーに分割してゆく。最上位のサブツリーはそのノードを含まない二分木の半分で構成される。次のサブツリーはそのノードを含まない残りのツリーの半分で構成される。ノード 0011 の例ではサブツリーは円で囲まれ、それぞれのプレフィクスが 1, 01, 000 および 0010 を持つ全てのノードで構成されている。

Kademlia のプロトコルでは、サブツリーにノードが含まれているのであれば各ノードはそのサブツリー内の少なくとも 1 つのノードを確実に認識するように保証している。この保証によりどのノードでもそのノードの ID で他のノードの位置を特定することができる。Figure 2 はノード 0011 が下位のサブツリーと下位サブツリー内のコンタクトを見つけるために、自身が知っている最良のノードに連続的に問い合わせることでノード 1110 を検索する例を示している。

このセクションの残りの部分では検索アルゴリズムの詳細を詰めてより具体的なものにする。最初に ID の近接性の正確な概念を定義し、キーにもっとも近い \(k\) 個のノードに〈key, value〉ペアを格納して検索することについて説明する。そして、キーと一意のプレフィクスを共有するノードが存在しない場合や、特定のノードに関連付けられているサブツリーの一部が空の場合でも機能する検索プロトコルを示す。

2.1 XOR メトリクス

Kademlia の各ノードは 160 ビットのノード ID を持つ。ノード ID は今のところ単にランダムな 160 ビット識別子だが Chord と同じように構築することもできる。ノードが送信するすべてのメッセージにはノード ID が含まれているため受信者は必要に応じて送信者の存在を記録することができる。

キーもまた 160 ビットの識別子である。〈key, value〉ペアを特定のノードに割り当てるために Kademlia は 2 つの識別子間の距離の概念に依存している。2 つの 160 ビット識別子 \(x\) と \(y\) が与えられたとき、Kademlia は 2 つの識別子間の距離を整数 \(d(x,y)=x \oplus y\) として解釈されるビット単位の排他的論理和 (XOR) として定義する。

まず我々は XOR が非ユークリッドメトリクスであっても有効であることを記述する。\(x \ne y\) かつ \(\forall x, y: d(x,y)=d(y,x)\) であれば \(d(x,x)=0\), \(d(x,y) \gt 0\) であることは明らかである。XOR はまた \(d(x,y)+d(y,z) \ge d(x,z)\) という三角特性も提供する。三角特性は \(d(x,y) \oplus d(y,z) = d(x,z)\) および \(\forall a \ge 0, b \ge 0: a+b \gt a \oplus b\) という事実から生じる。

次に我々は XOR が二分木ベースのシステムの概要図で暗黙のうちに距離の概念を捉えていることを記述する。160 ビットの ID すべてが配置された二分木では、2 つの ID 間の距離の大きさはその両方を含む最小のサブツリーの高さとなる。木が完全に配置されていない場合、ID \(x\) にもっとも近い葉は ID \(x\) ともっとも長い共通プレフィクスを共有している葉である。その場合、\(x\) にもっとも近い葉は、木の空の枝に対応する \(x\) のビットを反転することによって得られる ID \(\tilde{x}\) にもっとも近い葉となる。

Chord の時計回りの円周メトリクスと同様に XOR は一方向である。任意の点 \(x\) と距離 \(\Delta \gt 0\) に対して \(d(x,y)=\Delta\) となるような点 \(y\) が正確に一つだけ存在する。この単方向性により元のノードに関係なく同じキーのすべての検索が同じ経路に沿って収束する。したがって検索経路に沿って〈key, value〉ペアをキャッシュすることでホットスポットが軽減される。Pastry と同様に、また Chord とは異なり、XOR トポロジーも対称 (すべての \(x\) と \(y\) に対して \(d(x,y)=d(y,x)\)) である。

2.2 ノード状態

Kademlia ノードはクエリーメッセージをルーティングするために互いのコンタクト情報を保存する。\(0 \ge i \gt 160\) ごとに、自分の位置に対して \(2^i\) から \(2^{i+1}\) の距離のノードの (IPアドレス, UDPポート, ノードID) の三値を保持する。これらのリストは \(k\)-bucket と呼ばれる。各 \(k\)-bucket はノードを参照した時刻 ─ つまりもっとも過去に参照したノード (least-recently seen node) が先頭、もっとも最近に参照したノード (most-recently seen node) が末尾となるようにソートされる。通常、小さな \(i\) の値に対して \(k\)-bucket は空となるだろう。(適切なノードが存在しないため)。\(i\) の値が大きい場合、リストはサイズ \(k\) まで大きくなることができる。\(k\) はシステム全体のレプリケーションパラメータである。\(k\) は、与えられた \(k\) 個のノードが互いに 1 時間以内に故障する可能性が非常に低くなるように選択される (例えば \(k=20\))。

Kademlia ノードは別のノードからメッセージ (リクエストまたは応答) を受信すると、送信者のノード ID に対応する適切な \(k\)-bucket を更新する。送信ノードが受信者の \(k\)-bucket にすでに存在する場合、受信者はそれをリストの末尾に移動する。ノードがまだ適切な \(k\)-bucket に存在せず、バケットのエントリが \(k\) 未満の場合、受信者は単に新しい送信者をリストの最後尾に追加するだけである。ただし、適切な \(k\)-bucket がいっぱいの場合、受信者は \(k\)-bucket のなかで最後に確認されたノードに ping を実行し何をすべきかを決定する。最後に確認されたノードが応答しなかった場合、そのノードは \(k\)-bucket から追い出され、新しい送信者が最後尾に挿入される。最後に確認されたノードが応答した場合、そのノードはリストの最後尾に移動され、新しい送信者のコンタクトは破棄される。

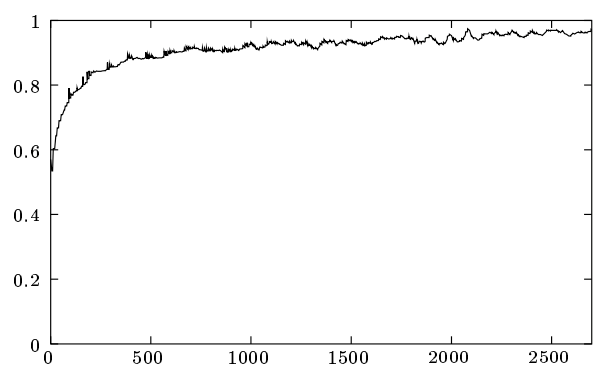
\(k\)-bucket はライブノードがリストから削除されることがないことを除いて、最後に確認されたノードの退避ポリシーを効率的に実装している。古いコンタクトを好む傾向は Saroiu ら [4] によって収集された Gnutella トレースデータの分析に基づいている。Fig. 3 はある時点からさらに 1 時間のオンラインを維持する Gnutella ノードの割合を駆動時間の関数として示している。ノードの駆動時間が長ければ長いほど、それからさらに 1 時間は駆動している可能性は高くなる。\(k\)-bucket はもっとも古いライブコンタクトを保持することによって、その中に含まれるノードがオンライン状態を維持する確率を最大化している。

\(k\)-bucket の 2 つ目の利点は特定の DoS 攻撃に対する耐性を提供することである。システムに新しいノードを大量に投入してノードのルーティング状態をフラッシュさせることはできない。Kademlia ノードは、古いノードがシステムを離れるときのみ \(k\)-bucket に新しいノードを挿入する。

2.3 Kademlia プロトコル

Kademlia のプロトコルは PING, STORE, FIND_NODE, FIND_VALUE の 4 つの RPC で構成されている。PING RPC はノードを試してオンラインであるかを確認する。STORE は後で検索できるように〈key, value〉ペアを保存するようノードに指示する。

FIND_NODE は 160 ビットの ID を引数に取る。RPC の受信者は目的の ID にもっとも近いことが分かっている \(k\) 個のノードの〈IPアドレス, UDPポート, ノードID〉の三値を返す。これらの三値は単一の \(k\)-bucket から取得することもできるが、もっとも近い \(k\)-bucket がいっぱいでない場合は複数の \(k\)-bucket から取得することもできる。いずれにしても RPC 受信者は \(k\) 個のアイテムを返す必要がある (すべての \(k\)-bucket を合計したノード数が \(k\) 個より少ない場合は別だが、その場合は認識しているすべてのノードを返す)。

FIND_VALUE は RPC 受信者がすでにそのキーの STORE RPC を受け取っているのであれば単に格納されている値を返し、そうでなければ FIND_NODE と同様に〈IPアドレス, UDPポート, ノードID〉の三値を返す動作をする。

すべての RPC で受信者は 160 ビットのランダムな RPC ID をエコーしなければならない。これによりアドレス偽造に対する耐性が得られる。PRC 受信者が送信者のネットワークアドレスに対する追加の確証を得るために RPC の応答で PING をピギーバックすることもできる。

Kademlia の参加者が実行しなければならないもっとも重要な手順は、指定されたノード ID にもっとも近い \(k\) 個のノードを見つけることである。この手順をノード検索と呼ぶ。Kademlia はノード検索に再帰的アルゴリズムを採用している。検索イニシエーターはもっとも近い空でない \(k\)-bucket から \(\alpha\) 個のノードを選択することから開始する (bucket のエントリ数が \(\alpha\) より少ない場合は、知っているもっとも近い \(\alpha\) 個のノードを選択する)。次に、イニシエーターは選択した \(\alpha\) 個のノードに並列で非同期 FIND_NODE RPC を送信する。\(\alpha\) は例えば 3 などのシステム全体の並列数パラメータである。

再帰ステップでは、イニシエーターが過去の RPC から学習したノードに FIND_NODE を再送する (この再帰ステップは前の RPC の \(\alpha\) すべてが戻る前に開始することができる)。イニシエーターはターゲットにもっとも近いことを知っている \(k\) 個のノードのうち、まだ問い合わせをしていない \(\alpha\) 個をピックアップし、それらのノードに FIND_NODE RPC を再送する¹。迅速に応答しないノードは応答があるまでは考慮から除外される。FIND_NODE ラウンドですでに見つけているもっとも近いノードよりも近いノードを返すことに失敗した場合、イニシエータはまだ問い合わせをしていないもっとも近い \(k\) 個のノードのすべてに FIND_NODE を再送する。検索はイニシエータが照会し、既知のもっとも近い \(k\) 個のノードからの応答を得た時点で終了する。\(\alpha=1\) の場合、この検索アルゴリズムはメッセージコストと障害ノード検出のレイテンシーの観点で Chord と似ている。しかし Kademlia はリクエストを転送するノードを \(k\) 個の中から任意の 1 つを選択できる柔軟性を備えているため、より低いレイテンシーでルーティングを行うことができる。

ほとんどの操作は上記の検索手順に基づいて実装されている。参加者は〈key, value〉ペアを格納するためにキーにもっとも近い \(k\) 個のノードを探し出し、それらに STORE RPC を送信する。さらに、Section 2.5 で述べるように各ノードは必要に応じて〈key, value〉ペアを再発行しそれらを維持する。これにより非常に高い確率で〈key, value〉ペアの永続性が保証される (証明の概略で示す)。Kademlia の現在のアプリケーション (ファイル共有) では〈key, value〉ペアの大本の発行者が 24 時間ごとに再発行するように要求している。そうしないと〈key, value〉ペアは公開から 24 時間で有効期限が切れ、システム内の古くなったインデックス情報を制限している。デジタル証明書や暗号論的ハッシュから値へのマッピングなど、他のアプリケーションでは有効期限を長く設定することが適切かもしれない。

〈key, value〉ペアを見つけるために、ノードはキーにもっとも近い ID を持つ \(k\) 個のノードを見つけるための検索を実行することから開始する。ただし値の検索では FIND_NODE RPC ではなく FIND_VALUE を使用する。さらに、任意のノードが値を返すと手続きは直ちに停止する。キャッシングの目的で、一度検索が成功すると要求ノードは観測されたキーにもっとも近いが値を返さなかったノードに〈key, value〉ペアを保存する。

トポロジーには単一方向性があるため、将来に同じキーを検索するともっとも近いノードに問い合わせる前にキャッシュされたエントリにヒットする可能性がある。特定のキーの人気が高いときには、システムの多くのノードがそのキーをキャッシュしている可能性がある。"オーバーキャッシング" を避けるためノードのデータベース内の〈key, value〉ペアの有効期限を現在のノードとキー ID にもっとも近いノードの間のノード数に指数関数的に反比例させる²。単純な LRU の退避でも同様のライフタイム分布が得られるが、ノードにはシステムが保存する値の数に関する事前情報がないため、キャッシュサイズを選択する自然な方法はない。

バケットは通常、ノードを通過するリクエストのトラフィックによって新鮮な状態に保たれる。特定の ID 範囲に対する検索がまったくないといった病的なケースに対処するために、各ノードは過去 1 時間にノード検索を実行していないバケットをリフレッシュする。リフレッシュとは、バケットの範囲内のランダムな ID を選択し、その ID に対するノード検索を行うことを意味する。

ネットワークに参加するには、ノード \(u\) はすでに参加しているノード \(w\) のコンタクトを持っている必要がある。まず \(u\) は適切な \(k\)-bucket に \(w\) を挿入する。次に \(u\) は自身のノード ID のノード検索を実行する。最後に \(u\) はもっとも近い隣接ノードよりも離れているすべての \(k\)-bucket をリフレッシュする。リフレッシュの間 \(u\) は必要に応じて自分の \(k\)-bucket を埋め、他のノードの \(k\)-bucket に自分自身を挿入する。

• ¹bucket のエントリと FIND 応答は \(\alpha\) 個のノードの選択に使用するためにラウンドトリップ時間の見積もりで拡張できる。
• ²この数値は現在のノードのバケット構造から推測できる。

2.4 ルーティングテーブル

Kademlia の基本的なルーティングテーブルの構造はプロトコルを考えるとかなり分かりやすいものだが、非常に不均衡なツリーを扱うために少し微妙な工夫が必要である。ルーティングテーブルは葉に \(k\)-bucket を持つ二分木である。各 \(k\)-bucket には共通の ID プレフィクスを持つノードが含まれている。プレフィクスは二分木における \(k\)-bucket の位置である。したがって各 \(k\)-bucket は ID 空間のいくつかの範囲をカバーしており、\(k\)-bucket は 160 ビットの ID 空間全体をオーバーラップすることなくカバーしている。

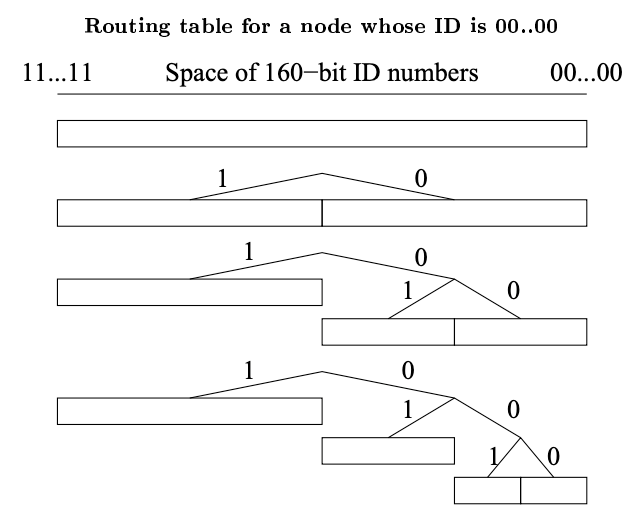
ルーティングツリーのノードは必要に応じて動的に割り当てられる。Fig. 4 にそのプロセスを示す。初期状態でノード \(u\) のルーティングツリーには単一の葉、つまり ID 空間全体をカバーする 1 つの \(k\)-bucket のみが存在する。\(u\) が新しいコンタクトを知ると適切な \(k\)-bucket にそのコンタクトを挿入しようと試みる。そのバケットがいっぱいでなければ新しいコンタクトは単に挿入されるだけである。そうでなければ、もし \(k\)-bucket の範囲に \(u\) ノード自身が含まれているならそのバケットは 2 つのバケットに分割され、以前の内容が 2 つバケットに分配される挿入の試行が繰り返される。範囲に自身を含んでいない \(k\)-bucket がいっぱいであれば新しいコンタクトは単純に破棄される。

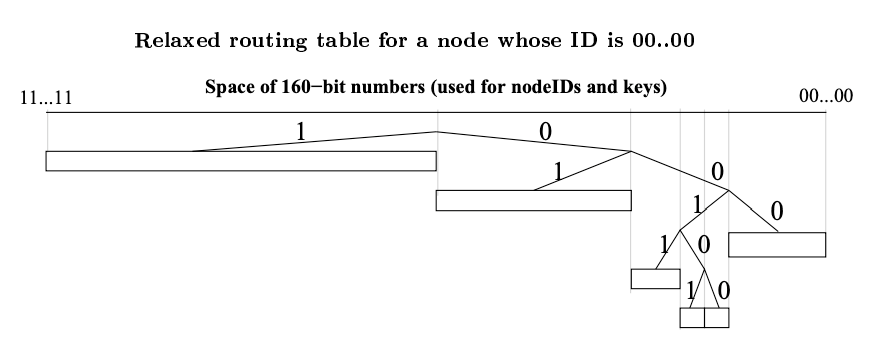
非常に不均衡なツリーでは 1 つの複雑な問題が発生する。ノード \(u\) がシステムに参加し、ID が 000 で始まる唯一のノードであり、システムにはすでにプレフィクス 001 を持つノードが \(k\) 個以上あると想定する。プレフィクス 001 を持つすべてのノードは \(u\) が挿入されるべき範囲に空の \(k\)-bucket を持っているが、\(u\) のバケットリフレッシュでは \(k\) 個のノードにしか通知されない。Kademlia ノードはこの問題を回避するために、ノード自身の ID が存在しないバケットを分割する必要がある場合でも、少なくとも \(k\) 個以上のノードサイズのサブツリーにすべての有効なコンタクトを保持する。Fig. 5 はこのような追加の分割を示している。\(u\) が分割バケットをリフレッシュするとプレフィクス 001 を持つすべてのノードがそれを知ることになる。

2.5 効率的なキーの再発行

ノードはキーと値のペアの永続性を確保するために定期的にキーを再発行する必要がある。そうしないと 2 つの現象により有効なキーの検索に失敗する可能性がある。第一に、発行されたキーと値のペアを最初に取得した \(k\) 個のノードの一部がネットワークから離脱する可能性がある。第二に、キーと値のペアが最初に発行されたノードよりも、発行されたキーに近い ID を持つ新しいノードがネットワークに参加する可能性がある。どちらの場合もキーと値のペアを持つノードは、キーにもっとも近い \(k\) 個のノードで利用できるように、再度キーと値のペアを再発行する必要がある。

Kademlia はネットワークを離脱するノードを補うためにそれぞれのキーと値のペアを 1 時間に 1 回再発行する。この戦略を単純に実装すると、キーと値のペアを格納している最大 \(k\) 個のノードが 1 時間ごとにノード検索と \(k-1\) 回の STORE RPC を実行することになり多くのメッセージが必要となる。幸い、この再発行プロセスは大幅に最適化することができる。まず、あるノードが特定のキー-値ペアの STORE RPC を受信すると、その RPC は他の \(k-1\) 番目に近いノードにも発行されたと想定し、受信者は次の 1 時間ではそのキー-値ペアを再発行しない。これにより再発行間隔が正確に同期していない限り、1 時間ごとに 1 つのノードのみが指定されたキーと値のペアを再発行することが保証される。

2 つ目の最適化は、キーを再発行する前にノード検索を行わないことである。Section 2.4 で説明したように、不均衡なツリーを処理するためにノードは必要に応じて \(k\)-bucket を分割し、少なくとも \(k\) 個のノードを持つ周囲のサブツリーを完全に認識できるようにしている。キーと値のペアを再発行する前に、ノード \(u\) が \(k\) 個のノードからなるこのサブツリー内のすべての \(k\)-bucket をリフレッシュすると、与えられたキーにもっとも近い \(k\) 個のノードを自動的に見つけ出すことができる。これらのバケットのリフレッシュは多くのキーの再発行で償却することができる。

サイズが \(k\) を超えるサブツリーでバケットをリフレッシュしたあとにノード検索が不要となる理由を確認するには 2 つのケースを考慮する必要がある。再発行されるキーがサブツリーの ID 範囲内に存在する場合、サブツリーのサイズは少なくとも \(k\) であり、\(u\) はサブツリーの完全な知識を持っているため \(u\) はキーにもっとも近い \(k\) 個のノードを知っている必要がある。一方、キーがサブツリーの外にあるにも拘らず \(u\) がキーにもっとも近い \(k\) 個のノードの 1 つであった場合、サブツリーよりもキーに近い区間の \(u\) の \(k\)-bucket はすべて \(k\) 未満のエントリである必要がある。したがって \(u\) はこれらの \(k\)-bucket に含まれるすべてのノードを知っていることになり、サブツリーの知識と併せてキーにもっとも近い \(k\) 個のノードを含むこととなる。

新しいノードがシステムに参加しようとしているとき、そのノードは自身ともっとも近い \(k\) 個のキーと値のペアを格納する必要がある。既存のノードも同様に周囲のサブツリーの完全な知識を活用することで新しいノードが格納すべきキーと値のペアを知ることができる。したがって、新しいノードを学習するノードは STORE RPC を発行して関連するキーと値のペアを新しいノードに転送する。ただし、ノードは冗長な STORE RPC の重複を避けるために自身の ID が他のノードの ID よりもキーに近い場合のみキーと値のペアを転送する。

3 証明の概略図

我々のシステムが適切に機能することを実証するために、ほとんどの操作がある定数 \(c\) に対して \(\lceil \log n \rceil + c\) 時間かかること、そして〈key, value〉検索がシステムに格納されているキーを確かな確率で返すことを証明する必要がある。

まずいくつかの定義から始める。距離範囲 \([2^i,2^{i+1})\) をカバーする \(k\)-bucket について、バケットのインデックスを \(i\) と定義する。ノードの深さ \(h\) を \(160-i\) と定義し、\(i\) は空でないバケットの最小のインデックスとする。ノード \(x\) でのノード \(y\) のバケット高を、\(x\) が \(y\) を挿入するであろうバケットのインデックスから \(x\) の空のバケットのもっとも小さいインデックスを引いたものとして定義する。ノード ID はランダムに選ばれることから非常に不均一な分布になる可能性は低い。したがって、ある任意のノードの高さは \(n\) 個のノードを持つシステムでは確かな確率で \(\log n\) の定数内となるだろう。さらに、\(k\) 番目に近いノード ID にもっとも近いノードのバケット高はおそらく \(\log k\) の定数内に収まるだろう。

次のステップでは、ノードが適切な範囲に存在する場合、すべてのノードのすべての \(k\)-bucket に少なくとも 1 つのコンタクトが含まれるという不変条件を仮定する。この仮定を前提としてノードの検索手順が正しく対数時間かかることを示す。ターゲット ID にもっとも近いノードの深さを \(h\) とする。このノードの最上位 \(h\) 個の \(k\)-bucket のいずれも空でない場合、検索手続きはステップごとに半分近くの (つまり距離が 1 ビット近い) ノードを見つけ出し、\(h-\log k\) ステップでそのノードを探し出すことになる。ノードの \(k\)-bucket の 1 つが空の場合、目的のノードが空のバケットの範囲内に存在する可能性がある。この場合、最後のステップで距離が半分になることはない。しかし、空のバケットに対応するキーのビットが反転されたかのように、検索は正確に進行する。したがって検索アルゴリズムは \(h-\log k\) ステップで常にもっとも近いノードを返します。さらに、もっとも近いノードが見つかると同時実行性は \(\alpha\) から \(k\) に切り替わる。残りの \(k-1\) 個のもっとも近いノードを見つけるためのステップ数は \(k\) 番目にもっとも近いノードの中のもっとも近いノードのバケット高以上になることはなく、定数プラス \(\log k\) 以上になることはほとんどないだろう。

この不変条件が正しいことを証明するには、まず不変条件が成立する場合のバケットのフレッシュの影響を検討する。フレッシュ後、バケットには \(k\) 個の有効なノードが含まれるか、\(k\) 個より少ない場合はその範囲内のすべてのノードが含まれている。(これはノードの検索手順が正しいことに起因する。) 新しく参加するノードは満杯ではないバケットにも挿入される。したがって、不変条件に違反する唯一の方法は、特定のバケットの範囲内に \(k+1\) 以上のノードが存在し、実際にバケットに含まれている \(k\) 個が検索やリフレッシュを介さずにすべて失敗することである。ただし、\(k\) は 1 時間 (最大リフレッシュ時間) 以内の同時故障の確率が低くなるように正確に選ばれている。

ノードのバケットはリクエストの受信または送信のたびに更新されるため、実際には故障の確率は 1 時間以内に \(k\) 個のノードが離脱する確率よりも遥かに小さくなる。これは XOR メトリクスの対称性に起因する。なぜなら、あるノードがリクエストの受信中または送信中に通信するノードの ID がそのノードのバケット範囲と正確に一致して分散しているためである。

さらに、単一ノードの単一バケット上で不変条件が失敗したとしても、これは (いくつかの検索にホップを追加することで) 実行時間に影響を与えるだけで、ノード検索の正確さには影響しない。検索を失敗させるには、検索経路上の \(k\) 個のノードがそれぞれ同じバケット内の \(k\) 個のノードを喪失する必要がある。異なるノードのバケットに重複がなければこれは \(2^{-k^2}\) の確率で発生する。そうでければ他の複数のノードのバケットに現れるノードの駆動時間が長くなり故障の可能性は低くなる。

次に〈key, value〉ペアのリカバリについて考慮する。〈key, value〉ペアが公開されるとキーにもっとも近い \(k\) 個のノードに発行される。また 1 時間ごとにも再発行される。新しいノード (信頼性のもっとも低いノード) であっても 1 時間後には 1/2 の確率で持続するため、1 時間後には〈key, value〉ペアはキーにもっとも近い \(k\) 個のノードの 1 つに確率 \(1-2^{-k}\) で存在していることになる。この特性はキーに近い位置に新しいノードが挿入されても破られることはない。なぜなら、そのようなノードが挿入されるとすぐに、それらのノードはバケットをデータで埋めるためにもっとも近いノードにコンタクトし、それによって保存すべき近くの〈key, value〉ペアを受け取るためである。当然ながら、Kademlia はキーにもっとも近い \(k\) 個のノードが故障し〈key, value〉ペアが他の場所にキャッシュされていないケースではペアの格納に失敗してキーを失うことになる。

4 実装ノート

この章では Kademlia 実装のパフォーマンスを改善するために使用した 2 つの重要な技法について説明する。

4.1 最適化されたコンタクトアカウント

望ましい \(k\)-bucket の基本特性は有効なコンタクトを削除することなく無効なコンタクトの LRU チェックと削除を提供することである。Section 2.2 で説明したように、\(k\)-bucket が満杯の場合はバケットの範囲内の未知のノードからのメッセージを受信するたびに PING RPC を送信する必要がある。PING は \(k\)-bucket の中でもっとも最近使用されたコンタクトがまだ有効かどうかを確認する。有効でなければ新しいコンタクトが古いコンタクトを置き換える。残念ながら、前述のアルゴリズムではこの PING のために大量のネットワークメッセージが必要になる。

Kademlia はトラフィックを削減するために有益なメッセージを送信できるようになるまでコンタクトの有効性調査を遅らせるようにしている。Kademlia ノードが未知のコンタクトからの RPC を受信し、そのコンタクトの \(k\)-bucket がすでに \(k\) 個のエントリで満杯になっている場合、そのノードは新しいコンタクトを、古くなった \(k\)-bucket エントリと置き換えるためのノードの交換用キャッシュに配置する。次回、ノードが \(k\)-bucket 内のコンタクトを問い合わせたときに応答のないコンタクトを排除し交換用キャッシュ内のエントリで置き換えることができる。交換用キャッシュは最後に観測した時間でソートされ、もっとも最近に観測したエントリが置換候補として最大の優先度を持つ。

関連する問題として、Kademlia は UDP を使用しているためネットワークパケットが失われると有効なコンタクトが応答できなくなることがある。パケットロスはネットワークの輻輳を示すことが多いため、Kademlia は応答のないコンタクトをロックし、指数増加のバックオフ間隔以上に RPC を送信しないようにする。Kademlia の検索はほとんどの段階で \(k\) 個のノードのうちの 1 ノードからの応答だけで済むため、システムは通常、ドロップされた RPC を同じノードに再送することはない。

コンタクトが連続して 5 回の RPC に応答しない場合、そのコンタクトは古くなっているとみなされる。\(k\)-bucket がいっぱいでないか、その交換用キャッシュが空の場合、Kademlia は古いコンタクトを削除するのではなく、単にフラグを立てるだけである。これにより、ノード自身のネットワーク接続が一時的にダウンしてもそのノードの \(k\)-bucket が完全に無効になることはない。

4.2 高速化された検索

実装におけるもう一つの最適化は、ルーティングテーブルのサイズを大きくすることによって検索あたりのホップ数を少なくすることである。概念的には ID を一度に 1 ビットではなく \(b\) ビットずつ考慮することによって行われる。前述のように検索あたりの期待ホップ数は \(\log_2 n\) である。ルーティングテーブルのサイズを \(2^b \log_{2^b} n\) 個の \(k\)-bucket に増やすことで期待ホップ数を \(\log_{2^b} n\) に削減することができる。

Section 2.4 ではバケットが満杯でその範囲にノード自身の ID が含まれる場合に Kademlia は \(k\)-bucket を分割するという方法について説明した。しかしこの実装ではノード ID を含まない範囲を \(b-1\) レベルまで分割することもできる。例えば \(b=2\) の場合、ノードの ID を含まない ID 空間の半分は 1 回 (2つの範囲に) 分割され、\(b=3\) の場合、2 レベルで最大 4 つの範囲に分割される。一般的な分割ルールは、バケットの範囲にノード自身の ID が含まれているか、ルーティングツリー内の \(k\)-bucket の深さ \(d\) が \(d \not\equiv 0 \pmod{b}\) を満たす場合にノードは満杯の \(k\)-bucket を分割するというものである。(深さは \(k\)-bucket の範囲内のすべてのノードが共有するプレフィクスの長さにすぎない。) 現在の実装では \(b=5\) を使用している。

XOR ベースのルーティングは Pastry [1]、Tapestry [2]、Plaxton の分散探索アルゴリズム [3] の第一段階のルーティングアルゴリズムに似ているが、3 つとも \(b \gt 1\) に一般化すると複雑になる。XOR トポロジーがなければ同じプレフィクスを共有していても次の \(b\) ビット桁が異なるノード内のターゲットを発見するための追加のアルゴリズム構造が必要となる。3 つのアルゴリズムはすべて異なる方法でこの問題を解決しているが、それぞれに独自の欠点がある。これらはすべて \(O(2^b \log_{2^b} n)\) サイズのメインテーブルに加えて \(O(2^b)\) サイズのセカンダリルーティングテーブルを必要とする。これにより、ブートストラップとメンテナンスのコストが増加し、プロトコルが複雑化し、Pastry と Tapestry については正しさと一貫性の形式的な分析を複雑化し妨げている。Plaxton は証明があるが、このシステムは P2P のような障害の多い環境にはあまり向いていない。

5 まとめ

斬新な XOR ベースのメトリクストポロジーを備えた Kademlia は、証明可能な一貫性とパフォーマンス、レイテンシーを最小限に抑えるルーティング、および対称的な単一方向性トポロジーを組み合わせた最初の P2P システムである。Kademlia はさらに同時実行性パラメータ \(\alpha\) を導入する。これにより、非同期の最低レイテンシーのホップ選択と遅延のない障害回復に対して、一定の帯域幅とのトレードオフを可能にしている。最後に Kademlia はノードの障害が稼働時間に反比例するという事実を利用する最初の P2P システムである。

References

1. A. Rowstron and P. Druschel. Pastry: Scalable, distributed object location and routing for large-scale peer-to-peer systems. Accepted for Middleware, 2001, 2001. http://research.microsoft.com/~antr/pastry/.
2. Ben Y. Zhao, John Kubiatowicz, and Anthony Joseph. Tapestry: an infrastructure for fault-tolerant wide-area location and routing. Technical Report UCB/CSD-01-1141, U.C. Berkeley, April 2001.
3. Andréa W. Richa C. Greg Plaxton, Rajmohan Rajaraman. Accessing nearby copies of replicated objects in a distributed environment. In Proceedings of the ACM SPAA, pages 311–320, June 1997.
4. Stefan Saroiu, P. Krishna Gummadi and Steven D. Gribble. A Measurement Study of Peer-to-Peer File Sharing Systems. Technical Report UW-CSE-01-06-02, University of Washington, Department of Computer Science and Engineering, July 2001.
5. Ion Stoica, Robert Morris, David Karger, M. Frans Kaashoek, and Hari Balakrishnan. Chord: A scalable peer-to-peer lookup service for internet applications. In Proceedings of the ACM SIGCOMM ’01 Conference, San Diego, California, August 2001.

翻訳抄

二分探索木に基づき距離関数に XOR を使用する分散ハッシュテーブルアルゴリズム Kademlia に関する 2002 年の論文。ネットワーク全体では二分木の構造だが、個々のノードのルーティングテーブルはその部分木として見ることのできるリスト構造となる。ルーティングテーブルの参照先は \(k\)-bucket にまとめられ、駆動時間の長いノードは後の生存率も長いという統計的事実からどのノードを参照するかを決定する。

1. Maymounkov P., Mazières D. Kademlia: A Peer-to-Peer Information System Based on the XOR Metric. In: Druschel P., Kaashoek F., Rowstron A. (eds) Peer-to-Peer Systems. IPTPS 2002. Lecture Notes in Computer Science, vol 2429. Springer, Berlin, Heidelberg.