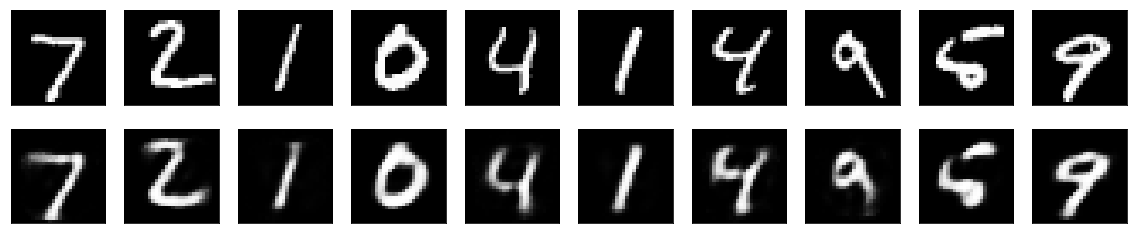Keras: 画像生成 (変分オートエンコーダー)

概要

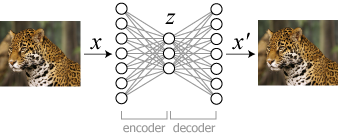
オートエンコーダー (autoencoder, 自動符号化器) はニューラルネットワークを使用した次元削減手法。次元の小さい中間層を設置した多層ニューラルネットワークを、入力と同じデータを出力するように学習することで、中間層部分の出力からより特徴的な表現を少ない次元で得ることができる。

オートエンコーダーは Fig.1 のように入力 \(x\) を潜在空間 \(z\) へ圧縮し、さらに \(x'\) へ復元するように学習する。

次元削減によって情報量が欠落するように見えるが、現実的なデータは冗長性を持っており、特徴を判別するためには不要な情報が多く含まれている。オートエンコーダーは元のデータを復元できる程度に不必要な特徴量を削除する。

次元削減は 1)過学習の回避 2)勾配消失の回避 3)計算量の削減などを目的にして行われる。

Keras のブログ Building Autoencoders in Keras よれば、現在のところオートエンコーダーが有用なタスクはノイズ除去と可視化のための次元削減である。

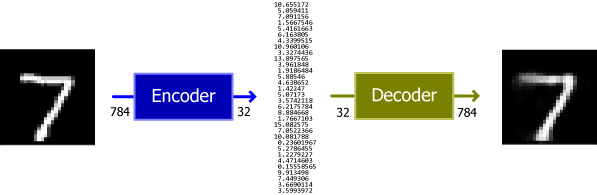
最もシンプルなオートエンコーダーは全結合層のエンコーダー/デコーダーのみで構成できる。Fig.2 は 28×28=784 ピクセルのグレイスケール MNIST 画像を 32個の特徴量に変換し、その特徴量から元の画像を復元している。

また Fig.3 は 10 個の手書き画像をオートエンコーダーを使用して復元したものである。これらは一度 32 次元の特徴量に変換されていることから MNIST の手書き画像データは 32 次元あれば表現可能であることを示唆している。

変分オートエンコーダー

変分オートエンコーダー (VAE; Variational Auto-Encoder) は概念ベクトルを使った編集タスクに適した生成モデル。エンコーダー-デコーダーモデルで構成され、エンコーダーネットワークは入力データを各次元がデータに関する属性の一部を表す低次元の潜在空間にエンコードし、続いてデコーダーネットワークがそれらの特徴量を元に元の入力を復元するように学習が行われる。

import keras
from keras import layers
from keras import backend as K
from keras.models import Model
import numpy as np

img_shape = (28, 28, 1)
batch_size = 16
latent_dim = 2

input_img = keras.Input(shape=img_shape)

x = layers.Conv2D(32, 3, padding="same", activation="relu")(input_img)
x = layers.Conv2D(64, 3, padding="same", activation="relu", strides=(2, 2))(x)
x = layers.Conv2D(64, 3, padding="same", activation="relu")(x)
x = layers.Conv2D(64, 3, padding="same", activation="relu")(x)
shape_before_flattening = K.int_shape(x)

x = layers.Flatten()(x)
x = layers.Dense(32, activation="relu")(x)

z_mean = layers.Dense(latent_dim)(x)
z_log_var = layers.Dense(latent_dim)(x)

def sampling(args):
  z_mean, z_log_var = args
  epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim), mean=0., stddev=1.)
  return z_mean + K.exp(z_log_var) * epsilon

z = layers.Lambda(sampling)([z_mean, z_log_var])

decoder_input = layers.Input(K.int_shape(z)[1:])
x = layers.Dense(np.prod(shape_before_flattening[1:]), activation="relu")(decoder_input)
x = layers.Reshape(shape_before_flattening[1:])(x)
x = layers.Conv2DTranspose(32, 3, padding="same", activation="relu", strides=(2, 2))(x)
x = layers.Conv2D(1, 3, padding="same", activation="sigmoid")(x)
decoder = Model(decoder_input, x)
z_decoded = decoder(z)

class CustomVariationalLayer(layers.Layer):
  def vae_loss(self, x, z_decoded):
    x = K.flatten(x)
    z_decoded = K.flatten(z_decoded)
    xent_loss = keras.metrics.binary_crossentropy(x, z_decoded)
    kl_loss = -5e-4 * K.mean(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
    return K.mean(xent_loss + kl_loss)

  def call(self, inputs):
    x = inputs[0]
    z_decoded = inputs[1]
    loss = self.vae_loss(x, z_decoded)
    self.add_loss(loss, inputs=inputs)
    return x

y = CustomVariationalLayer()([input_img, z_decoded])

from keras.datasets import mnist

vae = Model(input_img, y)
vae.compile(optimizer="rmsprop", loss=None)
vae.summary()

(x_train, _), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype("float32") / 255.
x_train = x_train.reshape(x_train.shape + (1,))
x_test = x_test.astype("float32") / 225.
x_test = x_test.reshape(x_test.shape + (1,))

vae.fit(x=x_train, y=None, shuffle=True, epochs=10, batch_size=batch_size, validation_data=(x_test, None))

import matplotlib.pyplot as plt
from scipy.stats import norm

n = 15
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))

for i, yi in enumerate(grid_x):
  for j, xi, in enumerate(grid_y):
    z_sample = np.array([[xi, yi]])
    z_sample = np.tile(z_sample, batch_size).reshape(batch_size, 2)
    x_decoded = decoder.predict(z_sample, batch_size=batch_size)
    digit = x_decoded[0].reshape(digit_size, digit_size)
    figure[i * digit_size: (i + 1) * digit_size, j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap="Greys_r")
plt.show()

参照

1. Francois Chollet (2018), PythonとKerasによるディープラーニング, マイナビ出版
2. 太田満久, 須藤広大, 黒澤匠雅, 小田大輔 (2018) TensorFlow開発入門 Kerasによる深層学習モデル構築手法, 翔泳社
3. CARL DOERSCH (2016), "Tutorial on Variational Autoencoders"
4. Keras: CNN中間総出力の可視化
5. Jaguar head shot-edit2.jpg CC BY-SA 3.0