多層パーセプトロン
 概要
概要
多層パーセプトロン (MLP; multilayer perceptron) または Feedforward Neural Network, Deep Feedforward Network は典型的な深層機械学習のためのネットワークモデル。多層パーセプトロンはある関数 \(f\) の近似を目的とし、写像 \(\vector{y} = f(\vector{x}; \vector{\theta})\) が最良の近似関数となるようなパラメータ \(\vector{\theta}\) を学習する。
このネットワークモデルはデータの流れが \(x\) の評価から \(f\) で定義される中間計算を経て \(y\) を出力することから Feedforward と呼ばれる。ただしネットワークモデルの出力がモデル自身にフィードバックされる方向の接続は存在しない。Feedforward Neural Network が自己フィードバックの接続をとるように拡張されたネットワークモデルは再帰型ニューラルネットワーク (RNN) と呼ばれる。
ニューラルネットワークはパーセプトロンと呼ばれる一般的な機械学習アルゴリズムから派生した。多くの層のパーセプトロンを組み合わせるたモデルは多層パーセプトロンまたは Feedforward Neural Network として知られている。
 パーセプトロン
パーセプトロン
パーセプトロンはニューラルネットワークを構成する最も基本的な要素である。式 (\(\ref{perceptron}\)) に示すように複数の入力 \(x_i\) に対して重み \(w_i\) を乗算して一つの値 \(y\) を出力する。ここで \(b\) はバイアス、\(\sigma(z)\) は活性化関数である。\[ \begin{equation} y = \sigma \left( b + \sum_{i=1}^n w_i x_i \right) \label{perceptron} \end{equation} \]
ベクトルプロセッサで演算を行う場合はバイアスを \(x_0=1\), \(w_0=b\) とした仮想的な入力とすると都合が良いだろう。
活性化関数はパーセプトロンの出力が微分可能な挙動に従うよう規定を設ける役割を持っている。これにより勾配降下法での最適解の学習を容易に行うことができる。一般的なパーセプトロンは出力は値の大小のみに意味があることから、単純増加の関数が適用されることが多い。
古典的なパーセプトロンでは重みづけられた入力の合計 \(\sum_i w_i x_i\) がある閾値 \(t\) より小さいか大きいかに基づいて 0 または 1 のどちらかを出力していた。これは活性化関数にステップ関数 (\(\ref{step_function}\)) を適用した場合と等価である。\[ \begin{equation} \sigma(z; t) = \left\{ \begin{array}{ll} 0 & \mbox{for} \ \ z \lt t \\ 1 & \mbox{for} \ \ z \geq t \end{array} \right. \label{step_function} \end{equation} \] しかしステップ関数は微分可能ではなく値の変化が緩やかでないことからシグモイドのような活性化関数が使用されている。
パーセプトロンは線形分類可能な問題を正しく表現することができる。また複数のパーセプトロンを組み合わせることで線形分類不可能な問題も表現することができる。複数のパーセプトロンを組み合わせたものは多層パーセプトロンと呼ばれる。
 活性化関数
活性化関数
活性化関数は各ノードの出力を規定するために \(b+\sum_{i=0}^m w_i x_i\) の線形変換を行った後に適用する非線形変換である。パーセプトロンが漸次学習 (progressive learning) とき、出力が大きく変化すると漸次的に最適解へ収束させることが困難になる。このため重みとバイアスをわずかに変化させたときに出力もわずかに変化しなければならない。
標準的な集積回路は入力に応じて 1 (オン) または 0 (オフ) を出力する活性化関数のネットワークとみることができる。これはニューラルネットワークにおける線形パーセプトロンの挙動に類似している。しかし、非線形の活性化関数のみが少数のノードを使用して重要な問題を計算することを可能にする。
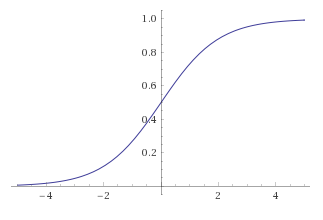
 シグモイド関数
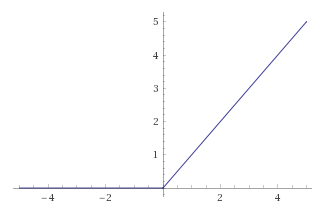
シグモイド関数 ReLU
ReLU-
正規化線形関数 (ReLU; rectified linear unit) またはランプ関数は非線形関数として表される。\[ f(x) = \max(0, x) = \left\{ \begin{array}{ll} 0 & \mbox{for} \ \ x \lt 0 \\ x & \mbox{for} \ \ x \geq 0 \end{array}\right. \] ReLU の微分は \(x=0\) を境界に 0 または 1 となることから、傾きを消去するか適用するかを判断する。シグモイド関数は入力が大きくなるにつれ傾きが小さくなっていたが、ReLU は一定の傾きを保ち続けることから勾配消失問題を緩和できる。
 損失関数
損失関数
損失関数はニューラルネットワークの出力に対する正解データとの差を算出する関数。ネットワークの学習時にのみ使用する。損失関数の返す値を損失または誤差と呼ぶ。この損失値はニューラルネットワークを逆方向に伝播する。
 MSE
MSE-
真の値と推定値との平均二乗誤差。この値は各推定値と真の値との誤差の平均値を表しており、誤りが大きくなったときに明確な差となるように二乗したもの。真の値を \(\vector{x}\)、対応する推定値を \(\vector{x}'\)、要素数 \(n\) としたとき以下のように表される。\[ {\rm MSE} = \frac{1}{n} \sum_{i=1}^n (x'_i - x_i)^2 \]
 バイナリクロスエントロピー
バイナリクロスエントロピー-
一般に 0.0~1.0 の範囲で真偽判定を行う 2 値分類に適した損失関数。真の値 \(x\), 推定値 \(x'\), \(0 \leq x \leq 1\), \(0 \leq x' \leq 1\) としたとき以下のように表される。\[ -x \log x' - (1 - x) \log (1 - x') \]
 カテゴリカルクロスエントロピー
カテゴリカルクロスエントロピー-
他クラス分類に適した対数損失を算出する関数。出力の活性化関数に softmax を前提としている。カテゴリ \(k \in \{1, \ldots, K\}\) における真の値 \(\vector{x}\)、推定値 \(\vector{x'}\) としたとき以下のように表される。\[ L_i = - \sum_{k=1}^K x_{i,k} \log x'_{i,k} \]
| 分類 | 最終層の活性化関数 | 損失関数 |
|---|---|---|
| 二値分類 | sigmoid | binary_crossentropy |
| 多クラス単一ラベル分類 | softmax | categorical_crossentropy |
| 多クラス多ラベル分類 | sigmoid | binary_crossentropy |
| 任意の値に対する回帰 | なし | mse |
| 0-1 の値に対する回帰 | sigmoid | mse または binary_crossentropy |
多ラベルは 1 つのサンプルに複数のラベルを付与できる問題を指す。