論文翻訳: LexRank: Graph-based Lexical Centrality as Salience in Text Summarization
Güneş Erkan\(^1\) gerkan@umich.edu
Dragomir R. Radev\(^{2,1}\) radev@umich.edu
\(^1\)Department of EECS, \(^2\)School of Information
University of Michigan, Ann Arbor, MI 48109 USA
 Abstract
Abstract
我々は推計学的な graph-based のグラフに基づいて自然言語処理におけるテキスト単位の相対的重要度を算出する方法を導入し、テキスト要約 (TS; text summarization) 問題でこの手法をテストする。抽出型要約 (extractive TS) は文書または文書セット内のもっとも重要な文を識別する要点文の概念に依る。典型的に、要点は特定の重要語の存在または疑重心文 (centroid pseudo-sentence) との類似性の観点で定義される。我々は文章のグラフ表現における固有ベクトル中心性をコンセプトとして文の重要度を計算する新しいアプローチである LexRank を考察する。このモデルは文に閉じたコサイン類似度に基づく連結性行列を文章のグラフ表現として隣接行列で表す。LexRank に基づいた我々のシステムは直近の DUC 2004 評価で 1 つ以上のタスクで 1 位にランクされた。本稿では我々のアプローチの詳細な分析を提示し、過去の DUC 評価でのデータを含むより大きなデータセットに適用する。我々は類似度グラフを用いて中心性を算出するためのいくつかの方法について論議する。結果は degree-based の方法 (LexRank を含む) が centroid-based の方法および DUC に参加したそれ以外のシステムの両方に対してほとんどのケースで優れていることを示している。さらに、しきい値 LexRank 法は連続 LexRank を含む degree-based 技法よりも優れいている。また我々のアプローチは、不完全な文書トピッククラスタリングに起因するデータのノイズに対して全く影響を受けないことも示している。
Table of Contents
- Abstract
- 1 Introduction
- 2 Sentence Centrality and Centroid-based Summarization
- 3 Centrality-based Sentence Salience
- 4 Experimental Setup
- 4.1 Data Set and Evaluation Method [under construction]
- 4.2 MEAD Summarization Toolkit [under construction]
- 5 Results and Discussion
- 5.1 Effect of Threshold on Degree and LexRank Centrality [under construction]
- 5.2 Comparision of Centrality Methods [under construction]
- 5.3 Experiments on Noisy Data [under construction]
- 6 Related Work [under construction]
- 7 Conclusion [under construction]
- Acknowledgements
- 翻訳抄
 1 Introduction
1 Introduction
近年の自然言語処理 (NLP) は非常に強固な数学的な基盤に移行した。NLP での多くの問題、例えば解析[Col97]、語義の曖昧性解消[Yar95]および自動言い換え[BL03]は堅牢な統計的手法の導入によって大幅に恩恵を受けている。NLP に対する堅牢なグラフに基づいた最近の方法も、例えば単語クラスタリング[BiW02]や前置詞フレーズ添付[TMN04]で多くの関心を集めている。
本稿では NLP でのグラフに基づいた方法を更に進める。我々は文ベースのグラフ上でのランダムウォークがテキストの要約にどのように役立つかを説明する。また我々は名前付けエンティティ分類、前置詞フレーズ負荷、テキスト分類 (例えばスパム認識など) などの他の NLP タスクに同様の技術をどmのように適用できるかを簡単に説明する。
テキスト要約はユーザに有用な情報を提供するために特定のテキストの圧縮版を自動で生成する処理である。要約の情報内容はユーザのニーズに依存する。トピック指向の要約はユーザの関心トピックに焦点を当てて、指定されたトピックに関連するテキスト内の情報を抽出する。一方、一般的な要約は、元のテキストから一般的なトピック攻勢を維持しながら、できるだけ多くの情報コンテンツをカバーしようとする。本稿では、複数のドキュメントを抽出する一般的なテキストのような国焦点を当てる。ここでの目的は同じであるが不特定なトピックについて複数のドキュメントの要約を生成することである。
抽出型要約は元の文書内の文のサブセットを選択することによって要約を生成する。これはテキスト内の情報の言い換えが行われる抽象型要約とは対照的である。二兎に寄って作成された要約は通常抽出型要約ではないが、今日の殆どの要約研究は抽出型要約である。純粋な抽出型要約は自動の概念的な要約に比べてしばしば優れた結果をもたらす。これは、意味論的表現、推論、自然言語生成などの抽象型要約における問題が、文抽出などのデータ駆動型アプローチに比べて比較的困難であるという事実による。実際、抽象型要約は今日に至って成熟段階に達していない。既存の抽象型要約生成器は抽象化の前処理の要素に依存する部分が大きい。抽出処理の出力は切り貼りされるかまたは圧縮されてテキストの要約が生成される[WM99, Jin02, MK00]。SUMMONS[RM98]は複数のソースから情報を抽出して結合し、この情報を言語生成コンポーネントに渡して最終的なサマリを生成する複数文書サマライザの例である。
抽出型要約の初期の研究は文章中の位置、文章の全体的な頻度、文の重要性を示す幾つかのフレーズ[Bax58, Edm69, Luh58]といった文の単純でヒューリスティックな特徴に基づいている。文中の単語の重要度を評価するためによく利用される手段は式[SJ72]で定義されている逆文書頻度、つまり IDF である: \[ {\rm idf}_i = \log \left( \frac{N}{n_i} \right) \] ここで \(N\) は文書集合に含まれる文書の総数であり、\(n_i\) は単語 \(i\) が出現する文書の数である。例えば、ほとんどすべての文書に出現する可能性が高い単語 (例えば "a" や "the" など) は IDF 値がゼロに近く、まれにしか出現しない単語 (医学用語、固有名詞など) は通常 IDF 値が高くなる。
より高度な技術では単語の同義語や首句反復 (anaphora) 解決[MB97, BE99]を用いて文章または談話構造の関係も考慮する。より多くの機能が提供されより多くの訓練データが利用可能になったことから、研究者は機械学習を要約に統合しようとしている[KPC95, Lin99, Osb92, DIM04]。
本稿ではクラスタに含まれる各文の中心性を評価し要約に含めるもっとも重要な文を抽出する。我々は文章の語彙的性質の点で中心性を測定する複数文書要約における語彙中心原理を定義する様々な方法を調査する。
第2章では文の中心性を判断するためによく知られた方法である重心に基づいた (centroid-based) 要約を提示する。次に、ソーシャルネットワークの「重要性」概念からインスピレーションを得た、中心性、次数 (Degree)、しきい値付き LexRank、連続 LexRank の 3 つの新しい尺度を導入する。本論文では文書クラスタのグラフ表現を提案する。このグラフの頂点は文を表し、辺は文の間の類似性関係で定義される。この表現によりグラフ上に定義されたいくつかの中心性ヒューリスティックが利用できるようになる。我々の方法と重心に基づいた方法での要約を、機能ベースの汎用集計ツールキット MEAD を使用して比較し、ほとんどのケースで新しい方法が重心法より優れていることを示す。我々の実験のデータは 2003 年および 2004 年の DUC (Document Understanding Conferences) の要約評価から得られ、我々のシステムと他の最先端の要約システムおよび人間のパフォーマンスとを比較する。
 2 Sentence Centrality and Centroid-based Summarization
2 Sentence Centrality and Centroid-based Summarization
抽出型要約は元の文書に含まれる文のサブセットを選択することによって機能する。この処理は、クラスタの主旨となるテーマに関連して必要かつ十分な量の情報をもたらす、(複数文書) クラスタ内で最も中心の文を特定するものとみなすことができる。文の中心性はそれが含んでいる単語の中心性の観点から定義されることが多い。単語の中心性を評価する一般的な方法はベクトル空間内の文書クラスタの重心を見ることである。クラスタの重心は \({\rm tf}\times{\rm idf}\) スコアが事前定義されているしきい値を上回る単語からなる疑似文書である。ここで \({\rm tf}\) はクラスタ内の単語の頻度、\({\rm idf}\) 値は通常はるかに大きな類似のジャンルデータセットに渡って計算される。centroid-based 要約[RJB00]ではクラスタの重心からより多くの単語を含む文が中心とみなされる (Algorithm 1)。これは文がクラスタの重心にどの程度近いかを示す尺度である。centroid-based 要約は過去に有望な結果をもたらし、最初の web-based 複数文書概要システム[※1][RGBZ01]となった。
input : An array S of n sentences, cosine threshold t
output: An array C of Centroid scores
Hash WordHash;
Array C
/* compute tf×idf scores for each word */
for i ← 1 to n do
foreach word w of S[i] do
WordHash{w}{"tfidf"} = WordHash{w}{"tfidf"} + idf{w};
end
end
/* construct the centroid of the cluster */
/* by taking the words that are above the threshold*/
foreach word w of WordHash do
if WordHash{w}{"tfidf"} > t then
WordHash{w}{"centroid"} = WordHash{w}{"tfidf"};
end
else
WordHash{w}{"centroid"} = 0;
end
end
/* compute the score for each sentence */
for i ← 1 to n do
C[i] = 0;
foreach word w of S[i] do
C[i] = C[i] + Wordhash{w}{"centroid"};
end
end
return C;
Algorithm 1: Computing Centroid scores.
※1システム: http://www.newsinessence.com
 3 Centrality-based Sentence Salience
3 Centrality-based Sentence Salience
この章では文の要点を評価するための他のいくつかの基準を提案する。我々のアプローチはすべてソーシャルネットワークの重要性[※2] (prestige) というコンセプトに基づいている。ソーシャルネットワークはコンピュータネットワークや情報検索に多くのアイデアをもたらした。ソーシャルネットワークは相互作用するエンティティ (人、組織、コンピュータなど) 間の関係のマッピングである。ソーシャルネットワークはグラフとして表され、ノードはエンティティを表し、リンクはノード間の関係を表している。
文書クラスタは相互に関連する文のネットワークと見なすことができる。いくつかの文は互いに類似しているが、それ以外は文の残りとわずかな情報しか共有しない場合もある。我々は、クラスタ内の他の多くの文に類似した文が、トピックにとってより中心的 (または要点) であるという仮説を立てる。この中心性の定義において明確にするべき点が 2 つある。まず 2 つの文の間の類似性を定義する方法、次に他の文との類似性を考慮して文全体の中心性を算出する方法である。
類似性を定義するために、我々は \(N\) 次元ベクトルでそれぞれの文を表す bag-of-words モデルを使用する。ここで \(N\) は対象とする言語のとり得る全ての単語の数である。文に出現するそれぞれの単語について、文のベクトル表現に対応する次元の値は文中の単語の出現回数と単語の IDF の乗算である。このとき 2 つの文の類似性は 2 つの対応するベクトル間のコサインによって定義される。\[ {\rm idf\_modified\_cosine}(x,y) = \frac{ \sum_{w \in x,y} {\rm tf}_{w,x} {\rm tf}_{w,y} ({\rm idf}_w)^2 }{ \sqrt{ \sum_{x_i \in x} ({\rm tf}_{x_i,x} {\rm idf}_{x_i})^2 } \times \sqrt{ \sum_{y_i \in y} ({\rm tf}_{y_i,y} {\rm idf}_{y_i})^2 } } \] ここで \({\rm tf}_{w,s}\) は文 \(s\) における単語 \(w\) の出現回数を表す。
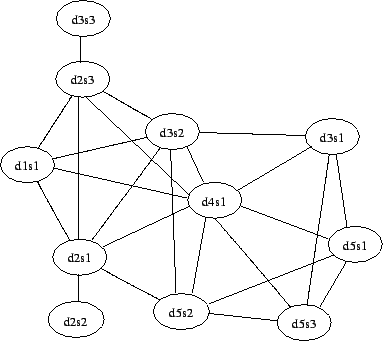
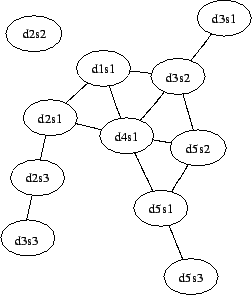
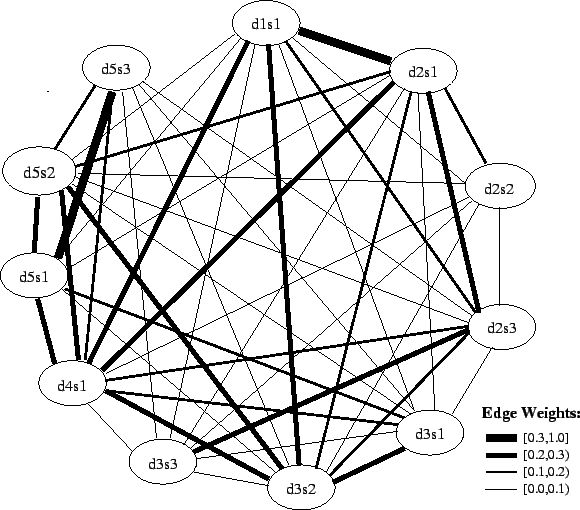
文書クラスタは、行列の各エントリが文ペア間の類似度に相当するコサイン類似度行列によって表すことができる。Figure 1 は DUC 2004 で使用されたクラスタのサブセットとそれに対応するコサイン類似度行列を表している。文 ID d\(X\)s\(Y\) は \(X^{\rm th}\) 番目の文書の \(Y^{\rm th}\) 番目の文を示している。この行列は、各エッジが文ペア間のコサイン類似度となる重み付きグラフでも表すことができる (Figure 2)。我々は以降の章でコサイン類似度行列および対応するグラフ表現を用いていくつかの文中心性の算出方法を論議する。
※2重要性: ``Prestige" and ``centrality" stand for the same concept with the difference that the former is often defined for directed graphs whereas the latter is defined for undirected graphs.
 3.1 Degree Centrality
3.1 Degree Centrality
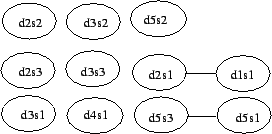
関連文書クラスタ内では文の多くが同一のトピックに関するものであるため、文の多くはお互いにやや似ていることが予想される。これは Figure 1 において類似行列の値の大部分が非ゼロ値であることから分かる。我々は有意な類似性に関心があることから、クラスタを、クラスタの各文がノードであり有意に類似した文が互いに接続している (無向) グラフとしてみなすために、しきい値を定義することによって行列内のいくつかの低い値を排除する。Figure 3 は、Figure 1 における類似度がそれぞれ 0.1, 0.2, 0.3 を超える文ペアが互いに類似していると仮定して導かれた隣接行列に対応するグラフを示している。すべての文はそれ自体に類似していることからも、グラフ中の全てのノードに対する自己リンクが存在しなければならないことに注意。我々は読みさすさのために自己リンクを省略するが、次の章での引数はそれらが存在することを前提としている。
Figure 3 のグラフから文書の中心性を評価する簡単な方法は、それぞれの文に類似した文を数えることだ。我々は類似度グラフ上で文に対応するノードの次数に対して文の次数中心性を定義する。Table 1 に見られるようにコサインしきい値の選択は中心性の解釈に劇的な影響を与える。低すぎるしきい値は誤った類似性を考慮させる可能性があるが、高すぎるしきい値もクラスタ内の類似関係の多くを失う可能性がある。
| ID | Degree (0.1) | Degree (0.2) | Degree (0.3) |
| d1s1 | 5 | 4 | 2 |
| d2s1 | 7 | 4 | 2 |
| d2s2 | 2 | 1 | 1 |
| d2s3 | 6 | 3 | 1 |
| d3s1 | 5 | 2 | 1 |
| d3s2 | 7 | 5 | 1 |
| d3s3 | 2 | 2 | 1 |
| d4s1 | 9 | 6 | 1 |
| d5s1 | 5 | 4 | 2 |
| d5s2 | 6 | 4 | 1 |
| d5s3 | 5 | 2 | 2 |
 3.2 Eigenvector Centrality and LexRank
3.2 Eigenvector Centrality and LexRank
次数中心を計算する場合、我々はそれぞれのエッジを各ノードの全体的な中心性の値を決定するための投票として扱う。これはそれぞれの投票カウントが同じになる全体的に民主的な方法である。しかし、多くのソーシャルネットワークではすべての関連が均等に重要というわけではない。例えば人々の交友関係によって相互に連結するソーシャルネットワークでは、人の重要性 (prestige) はその人に何人の友人がいるかのみに依存するのではなく、どのような人がその人の友人なのかにも依存する。
同様の考え方は抽出集約にも適用できる。次数の中心は、いくつかの望ましくない文章が互いに投票してその中心性を上げている場合、要約の質に悪影響を及ぼすことがある。極端な例として、すべての文書が互いに関連しているが、それらの中で一つのみが多少異なるトピックであるような雑音の多いクラスタを考える。当然ながら無関係な文書の文章をクラスタの一般的な要約に含めることは望ましくない。しかし、無関係な文書にはその文書の投票のみで考慮している非常に重要ないくつかの文が含まれていると仮定する。これらの文章は特定の文章からの局所的な投票によって人工的に高い中心性スコアを得るだろう。このような状況は、投票がどこから来ているかを考慮し、各投票で重み付けする際に投票ノードの中心性を考慮することによって避けることができる。この考えを定式化する直接的な方法は、中心値を有するすべてのノードを考慮し、この中心性をその隣接ノードに分配することである。これは以下の式で表される。\[ \begin{equation} p(u) = \sum_{v\in {\rm adj}[u]} \frac{p(v)}{{\rm deg}(v)} \label{dist_centrality} \end{equation} \] ここで \(p(u)\) はノード \(u\) の中心性、\({\rm adj}(u)\) はノード \(u\) に隣接しているノードの集合、\({\rm deg}(u)\) はノード \(u\) の次数。同様に式 (\(\ref{dist_centrality}\)) を行列で記述することもできる。\[ \begin{equation} \vector{p} = \vector{B}^T \vector{p} \label{eugen_vector_pbtp} \end{equation} \] あるいは \[ \begin{equation} \vector{p}^T = \vector{B} \vector{p}^T \label{eugen_vector} \end{equation} \] ここで行列 \(\vector{B}\) は、類似度グラフの隣接行列の各要素を対応する行の和で除算することで得られる。\[ \begin{equation} \vector{B}(i,j) = \frac{\vector{A}(i,j)}{\sum_k \vector{A}(i,k)} \end{equation} \]
行の合計は対応するノードの字数と等しいことに注意。すべての文が少なくともそれ自身と類似性をもっているためすべての行の合計はゼロにはならない。式 (\(\ref{eugen_vector}\)) は \(\vector{p}^T\) が固有値 \(\vector{1}\) に対応する行列 \(\vector{B}\) の左固有ベクトルであることを示している。そのような固有ベクトルが存在し個別に識別され計算されることを保証するために我々はいくつかの数学的な基礎知識を必要とする。
ある確率行列 \(\vector{X}\) をマルコフ連鎖の遷移行列とする。確率行列の要素 \(\vector{X}(i,j)\) は対応するマルコフ連鎖において状態 \(i\) から \(j\) の遷移確率を表している。確率の公理により、確率行列のすべての行は合計すると 1 になるはずである。\(\vector{X}^n(i,j)\) は第 \(n\) 遷移で状態 \(i\) から \(j\) へ移動する確率を与える。確率行列 \(\vector{X}\) のマルコフ連鎖は以下の条件で定常分布に収束する。\[ \lim_{n \to \infty} \vector{X}^n = \vector{1}^T \vector{r} \] ここで \(\vector{1} = (1, 1, \ldots, 1)\) であり、ベクトル \(\vector{r}\) はマルコフ連鎖の定常分布と呼ばれている。定常分布の直感的解釈はランダムウォークの概念に寄って理解することができる。マルコフ連鎖は、例えば全ての \(i\), \(j\) に対して \(\vector{X}^n(i,j) \neq 0\) が成り立つような \(n\) が存在するケースのように、任意の状態から他のあらゆる状態へ到達可能であれば既約である。マルコフ連鎖は、全ての \(i\) に対して \({\rm gcd}\{n: \vector{X}^n(i,i) \gt 0\} = 1\) であれば非周期的である。Perron-Frobenius 定理[Sen81]により既約で非周期的なマルコフ連鎖は固有の定常分布に収束することが保証されている。マルコフ連鎖が可約または周期的な要素を持つ場合、ランダム・ウォーカーはこれらの要素にスタックし、決してグラフの他の部分を訪れることはないだろう。
式 (\(\ref{eugen_vector_pbtp}\)) の類似行列 \(\vector{B}\) が確率行列の特性を満たすことから、我々はこれをマルコフ連鎖とみなすことができる。中心性ベクトル \(\vector{p}\) は定常分布 \(\vector{B}\) に対応する。しかし、我々は類似行列が常に規約で非周期であることを確認する必要がある。この問題を解くために Page ら[PBMW98]はグラフ内のどのノードにもジャンプする確率が引くことを示唆している。このようにしてランダム・ウォーカーは周期的または切断された要素から「脱出」することができ、グラフは既約かつ非周期的となる。グラフ内の任意のノードにジャンプする均一な確率を割り当てると、我々は式 (\(\ref{dist_centrality}\)) の修正である以下の式を導く。これは PageRank として知られている。\[ \begin{equation} p(u) = \frac{d}{N} + (1 - d) \sum_{v \in {\rm adj}[u]} \frac{p(v)}{{\rm deg}(v)} \label{page_rank} \end{equation} \] ここで \(N\) はグラフ内の全ノード数、\(d\) は一般的に \([0.1, 0.2]\)[BP98]の間で選択される「減衰係数」(dampling factor)である。式 (\(\ref{page_rank}\)) は以下の行列形式 \[ \begin{equation} \vector{p} = \left[ d\vector{U} + (1 - d) \vector{B} \right]^T \vector{p} \label{page_rank_matrix} \end{equation} \] で表すことができる。ここで \(\vector{U}\) はすべての要素が \(1/N\) と等しい正方行列である。マルコフ連鎖からもたらされる遷移カーネル \([d\vector{U} + (1-d)\vector{B}]\) は 2 つのカーネル \(\vector{U}\) と \(\vector{B}\) の混合である。このマルコフ連鎖のランダム・ウォーカーは確率 \(1-d\) で現在の状態に隣接する状態の一つを選択するか、もしくは確率 \(d\) で現在の状態を含んだグラフ内の任意の状態にジャンプする。PageRank の式は当初 Web ページの重要性を計算するために提案されたものであり Google の検索エンジンの背後にある基本的な仕組みとして機能している。
またマルコフ連鎖の収束特性はべき情報 (power method) と呼ばれる定常分布を計算するための単純なイテレーションアルゴリズムを提案する (Algorithm 2)。アルゴリズムは一様な分布から始まる。各イテレーションにおいて、固有ベクトルは確率行列の転置を掛けることによって更新される。マルコフ連鎖は規約で非周期的であるためアルゴリズムは終了することが保証される。
input : A stochastic, irreducible and aperoidic matrix M input : matrix size N, error tolerance ε output: eugen vector p p0 = 1/N 1 t = 0 repeat t = t + 1; pi = MT pt-1; δ = ||pi - pi-1||; until δ < ε return pi;
Algorithm 2: Power Method for computing the sationary distribution of a Markov chain.
元の PageRank 法とは異なり、コサイン類似度は対象関係であるため文に対する類似度グラフは無向である。しかし、これは定常分布の計算に何ら差異をもたらさない。我々はこれを文の新しい類似性尺度として lexical PageRank または LexRank と呼ぶ。Algorithm 3 は与えられた文集合の LexRank スコアを計算する方法の要約である。次数の中心性スコアも (Degree 配列内で) アルゴリズムの副産物として計算されることに注意。Table 2 は Figure 3 におけるグラフの減衰係数 \(0.85\) での LexRank スコアを示している。比較のために表には各文の重心スコアも記載している。最も高いランクの文がスコア 1 となるように全ての数値が正規化されている。これらの図から、しきい値の選択はいくつかの文の LexRank ランキングに影響することが明らかである。
input : An array S of n sentences, cosine threshold t
output: An array L of LexRank scores
Array CosineMatrix[n][n];
Array Degree[n];
Array L[n];
for i ← 1 to n do
for j ← 1 to n do
CosineMatrix[i][j] = idf-modified-cosine(S[i], S[j]);
if CosineMatrix[i][j] > t then
CosineMatrix[i][j] = 1;
Degree[i] ++;
end
else
CosineMatrix[i][j] = 0;
end
end
end
for i ← 1 to n do
for j ← 1 to n do
CosineMatrix[i][j] = CosineMatrix[i][j] / Degree[i];
end
end
L = PowerMethod(CosineMatrix, n, ε);
return L;
Algorithm 3: Computing LexRank scores.
| ID | LR (0.1) | LR (0.2) | LR (0.3) | Centroid |
| d1s1 | 0.6007 | 0.6944 | 1.0000 | 0.7209 |
| d2s1 | 0.8466 | 0.7317 | 1.0000 | 0.7249 |
| d2s2 | 0.3491 | 0.6773 | 1.0000 | 0.1356 |
| d2s3 | 0.7520 | 0.6550 | 1.0000 | 0.5694 |
| d3s1 | 0.5907 | 0.4344 | 1.0000 | 0.6331 |
| d3s2 | 0.7993 | 0.8718 | 1.0000 | 0.7972 |
| d3s3 | 0.3548 | 0.4993 | 1.0000 | 0.3328 |
| d4s1 | 1.0000 | 1.0000 | 1.0000 | 0.9414 |
| d5s1 | 0.5921 | 0.7399 | 1.0000 | 0.9580 |
| d5s2 | 0.6910 | 0.6967 | 1.0000 | 1.0000 |
| d5s3 | 0.5921 | 0.4501 | 1.0000 | 0.7902 |
 3.3 Continuous LexRank
3.3 Continuous LexRank
次数中心性と LexRank を計算するために構築した類似度グラフは重み付けされていない。これは適切なしきい値を使用してコサイン行列の 2 値離散化を行ったためである。あらゆる離散化操作と同様にこれは情報損失を意味している。LexRank の一つの改善は類似リンクの強さを利用することで得ることができる。コサイン値を直接使用して類似度グラフを作成すると、通常、より高密度で重み付けされたグラフが得られる (Figure 2)。遷移行列の行合計を使ってそれぞれの値を正規化することで確率行列を得ることができる。結果の式は LexRank 修正版となる重み付けグラフである。\[ \begin{equation} p(u) = \frac{d}{N} + (1 - d) \sum_{v \in {\rm adj}[u]} \frac{{\rm idf\_modified\_cosine}(u, v)}{\sum_{z \in {\rm adj}[v]} {\rm idf\_modified\_cosine}(z, v)} p(v) \end{equation} \] このようにして文の LexRank を計算する際に、我々はリンクしている文の LexRank 値 にリンクの重みを乗算する。重みは行の合計によって正規化され、メソッドの収束のために減衰係数が加算される。
 3.4 Centrality vs. Centroid
3.4 Centrality vs. Centroid
グラフに基づいた中心性は重心 (centroid) に比べていくつかの利点がある。まず第一に、それは文の間に情報の包含を説明している。文の情報内容がクラスタ内の別の文を包含する場合、要約にはより情報の多い方を含めることが当然望ましい。コサイン類似度グラフのノードの次数は、その文が他の文とどのくらいの共通情報を有するかの指標である。Figure 1 の文 d4s1 は、クラスタの最初の 2 つの文の情報をほぼ包含しており、他の文とも幾つかの共通の情報を持っているため、最も高いスコアを得ている。この提案手法のもう一つの利点は、不自然に高い IDF スコアがトピックに無関係な文のスコアを上げることを防ぐ点である。重心スコアを計算する際に単語の頻度が考慮されるが、高い IDF を持つような希少単語が多数含まれている文は、クラスタ内の他の場所に単語が存在しない場合でも高い重心スコアを付けることがある。
 4 Experimental Setup
4 Experimental Setup
この章では実験で使用したデータセット、評価基準および集計システムについて説明する。
 4.1 Data Set and Evaluation Method
4.1 Data Set and Evaluation Method
 4.2 MEAD Summarization Toolkit
4.2 MEAD Summarization Toolkit
 5 Results and Discussion
5 Results and Discussion
以下の章では公式 DUC データセットに対して行った実験の結果を類似性グラフに基づく中心性の異なる実装で示している。我々は MEAD の別の特徴として次数の中心性、しきい値を持つ LexRank および連続 LexRank を実装した。全ての特徴量は最高値を有する文がスコア 1 を獲得し、最低値を有する文がスコア 0 を得るように正規化される。すべての実行では MEAD の Length と Position の機能を、中心性の機能に加えてヒューリスティックをサポートする機能として使用した。カットオフ Length の値は 9 に設定した。つまり 9 ワード未満の文はすべて破棄される。Position 機能の重みはすべての実行において固定値 1 である。これらの 2 つのヒューリスティクスな特徴以外に、他の中心性の方法と組み合わせることなく、それぞれの中心性の特徴を単独で使用して、より良い比較をした。我々が実験しているそれぞれの中心性特徴に対して、対応する特徴の重みをそれぞれ 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 5.0, 10.0 に設定して 8 種類の MEAD 機能を実行した。
 5.1 Effect of Threshold on Degree and LexRank Centrality
5.1 Effect of Threshold on Degree and LexRank Centrality
 5.2 Comparision of Centrality Methods
5.2 Comparision of Centrality Methods
 5.3 Experiments on Noisy Data
5.3 Experiments on Noisy Data
 6 Related Work
6 Related Work
 7 Conclusion
7 Conclusion
 Acknowledgements
Acknowledgements
- [Bax58] P.B. Baxendale.
Man-made index for technical litterature - an experiment.
IBM J. Res. Dev., 2(4):354-361, 1958. - [BE99] Regina Barzilay and Michael Elhadad.
Using lexical chains for text summarization.
In Inderjeet Mani and Mark T. Maybury, editors, Advances in Automatic Text Summarization, pages 111-121. The MIT Press, 1999. - [BiW02] Chris Brew and Sabine Schulte im Walde.
Spectral clustering for german verbs.
In Proceedings of the 40th Annual Meeting of the Association for Computational Linguistics, 2002. - [BL03] Regina Barzilay and Lillian Lee.
Learning to paraphrase: An unsupervised approach using multiple-sequence alignment.
In Proceedings of HLT-NAACL, 2003. - [BMR95] Ron Brandow, Karl Mitze, and Lisa F. Rau.
Automatic condensation of electronic publications by sentence selection.
Information Processing and Management, 31(5):675-685, 1995. - [BP98] Sergey Brin and Lawrence Page.
The anatomy of a large-scale hypertextual Web search engine.
Computer Networks and ISDN Systems, 30(1-7):107-117, 1998. - [CG98] Jaime G. Carbonell and Jade Goldstein.
The use of MMR, diversity-based reranking for reordering documents and producing summaries.
In Research and Development in Information Retrieval, pages 335-336, 1998. - [Col97] Michael Collins.
Three generative, lexicalised models for statistical parsing.
In Proceedings of the 33rd Annual Meeting of the Association for Computational Linguistics, 1997. - [DIM04] Hal Daumé III and Daniel Marcu.
A phrase-based hmm approach to document/abstract alignment.
In Dekang Lin and Dekai Wu, editors, Proceedings of EMNLP 2004, pages 119-126, Barcelona, Spain, July 2004. Association for Computational Linguistics. - [Edm69] H.P. Edmundson.
New Methods in Automatic Extracting.
Journal of the Association for Computing Machinery, 16(2):264-285, April 1969. - [ER04a] Güneş Erkan and Dragomir R. Radev.
Lexpagerank: Prestige in multi-document text summarization.
In Dekang Lin and Dekai Wu, editors, Proceedings of EMNLP 2004, pages 365-371, Barcelona, Spain, July 2004. Association for Computational Linguistics. - [ER04b] Güneş Erkan and Dragomir R. Radev.
The University of Michigan at DUC 2004.
In Proceedings of the Document Understanding Conferences, Boston, MA, May 2004. - [HKH$^+$01] V. Hatzivassiloglou, J. Klavans, M. Holcombe, R. Barzilay, M. Kan, and K. McKeown.
Simfinder: A flexible clustering tool for summarization, 2001. - [Jin02] Hongyan Jing.
Using hidden markov modeling to decompose Human-Written summaries.
CL, 28(4):527-543, 2002. - [KM00] Kevin Knight and Daniel Marcu.
Statistics-based summarization -- step one: Sentence compression.
In Proceeding of The 17th National Conference of the American Association for Artificial Intelligence (AAAI-2000), pages 703-710, 2000. - [KPC95] Julian Kupiec, Jan O. Pedersen, and Francine Chen.
A trainable document summarizer.
In Research and Development in Information Retrieval, pages 68-73, 1995. - [LH03] Chin-Yew Lin and E.H. Hovy.
Automatic evaluation of summaries using n-gram co-occurrence.
In Proceedings of 2003 Language Technology Conference (HLT-NAACL 2003), Edmonton, Canada, May 27 - June 1, 2003. - [Lin99] C-Y. Lin.
Training a Selection Function for Extraction.
In Proceedings of the Eighteenth Annual International ACM Conference on Information and Knowledge Management (CIKM), pages 55-62, Kansas City, November -6 1999. ACM. - [Luh58] H.P. Luhn.
The Automatic Creation of Literature Abstracts.
IBM Journal of Research Development, 2(2):159-165, 1958. - [MB97] Inderjeet Mani and Eric Bloedorn.
Multi-document summarization by graph search and matching.
In Proceedings of the Fourteenth National Conference on Artificial Intelligence (AAAI-97), pages 622-628, Providence, Rhode Island, 1997. American Association for Artificial Intelligence. - MBE$[^+$01] Kathleen R. McKeown, Regina Barzilay, David Evans, Vasileios Hatzivassiloglou, Simone Teufel, Yen M. Kan, and Barry Schiffman.
Columbia Multi-Document Summarization: Approach and Evaluation.
In Proceedings of the 24th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, New Orleans, LA, 2001. - [MT04] Rada Mihalcea and Paul Tarau.
Textrank: Bringing order into texts.
In Dekang Lin and Dekai Wu, editors, Proceedings of EMNLP 2004, pages 404-411, Barcelona, Spain, July 2004. Association for Computational Linguistics. - [MTF04] Rada Mihalcea, Paul Tarau, and Elizabeth Figa.
Pagerank on semantic networks, with application to word sense disambiguation.
In Proceedings of The 20st International Conference on Computational Linguistics (COLING 2004), Geneva, Switzerland, August 2004. - [MUD99] Marie-Francine Moens, Caroline Uyttendaele, and Jos Dumortier.
Abstracting of legal cases: the potential of clustering based on the selection of representative objects.
J. Am. Soc. Inf. Sci., 50(2):151-161, 1999. - [Osb02] Miles Osborne.
Using Maximum Entropy for Sentence Extraction.
In ACL Workshop on Text Summarization, July 12-13, 2002. - [PBMW98] L. Page, S. Brin, R. Motwani, and T. Winograd.
The pagerank citation ranking: Bringing order to the web.
Technical report, Stanford University, Stanford, CA, 1998. - [Rad00] Dragomir Radev.
A common theory of information fusion from multiple text sources, step one: Cross-document structure.
In Proceedings, 1st ACL SIGDIAL Workshop on Discourse and Dialogue, Hong Kong, October 2000. - [RBGZ01] Dragomir Radev, Sasha Blair-Goldensohn, and Zhu Zhang.
Experiments in single and multi-document summarization using MEAD.
In First Document Understanding Conference, New Orleans, LA, September 2001. - [RJB00] Dragomir R. Radev, Hongyan Jing, and Malgorzata Budzikowska.
Centroid-based summarization of multiple documents: sentence extraction, utility-based evaluation, and user studies.
In ANLP/NAACL Workshop on Summarization, Seattle, WA, April 2000. - [RM98] Dragomir R. Radev and Kathleen R. McKeown.
Generating natural language summaries from multiple on-line sources.
Computational Linguistics, 24(3):469-500, September 1998. - [Sen81] E. Seneta.
Non-negative matrices and markov chains.
Springer-Verlag, New York, 1981. - [SJ72] K. Sparck-Jones.
A statistical interpretation of term specificity and its application in retrieval.
Journal of Documentation, 28(1):11-20, 1972. - S[SMB97] G. Salton, A. Singhal, M. Mitra, and C. Buckley.
Automatic Text Structuring and Summarization.
Information Processing & Management, 33(2):193-207, 1997. - [TMN04] Kristina Toutanova, Chris Manning, and Andrew Ng.
Learning random walk models for inducing word dependency distributions.
In Proceedings of ICML, 2004. - [WM99] Michael Witbrock and Vibhu O. Mittal.
Ultra-Summarization: A Statistical Approach to Generating Highly Condensed Non-Extractive Summaries.
In SIGIR99, pages 315-316, Berkeley, CA, 1999. - [Yar95] David Yarowsky.
Unsupervised word sense disambiguation rivaling supervised methods.
In Proceedings of the 33rd Annual Meeting of the Association for Computational Linguistics, 1995. - [Zha02] Hongyuan Zha.
Generic Summarization and Key Phrase Extraction Using Mutual Reinforcement Principle and Sentence Clustering.
In Proceedings of the 25th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Tampere, Finland, 2002.
翻訳抄
文書要約、自動要約アルゴリズム LexRank に関する 2004 年の論文。