word2vec

概要

分散表現 (distributed representation) とは単語の意味を数値化してベクトル空間に表すことである。単語をベクトル空間に埋め込むことから単語埋め込み (word embedding) とも呼ばれる。一般に分散表現によって一つの単語は数十～数百次元のベクトルに変換される。

word2vec [1] は分散表現を生成するためのアルゴリズムの一つである。このアルゴリズムは「単語の意味はその周辺の要素によって形成される」という分布仮説 (distributional hypothesis) に基づき、与えられた単語シーケンスの単語の位置関係から良好な分散表現を作成する。

Table of Contents

1. 概要
2. アルゴリズム
   1. 入力層
   2. 隠れ層
   3. 出力層
   4. バックプロパゲーション
   5. 結論
3. word2vec の利用
   1. text8 データセット
   2. 独自のデータセット
4. 参照

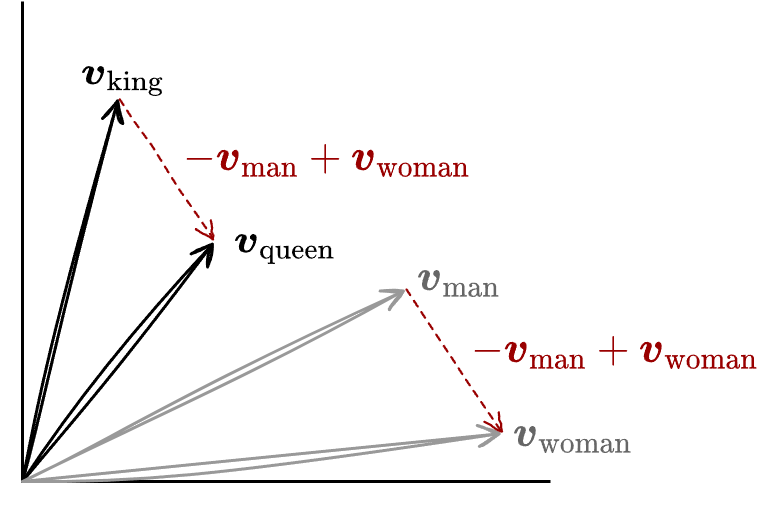
word2vec によって得られた単語ごとの数値は特徴空間上の点、つまり特徴ベクトルと見なすことができる。近接する点が意味的に類似し、その距離と方向も意味的な差異を表していることを示唆している。\(\vector{v}_{\rm X}\) を単語 X の特徴ベクトルとしたとき、Fig 2 に示すように \(\vector{v}_{\rm king} - \vector{v}_{\rm man} + \vector{v}_{\rm woman}\) の演算結果が \(\vector{v}_{\rm queen}\) の近傍になるという結果が経験的によく知られている。これは各単語の特徴ベクトル表現が現実の特徴を演算可能な差異として表していると考えることができる。

word2vec のアルゴリズムは自然言語処理のみならず遺伝子、コード、プレイリスト、ソーシャルグラフ、パターンとして認識可能なその他の言語または記号的系列にも同様に適用することができる。

アルゴリズム

word2vec は入力層、隠れ層、出力層の 3 層のニューラルネットワークで構成されている。入出力はともに単語であり、ある単語とその近傍の単語の生起確率が最適となるように学習させることで、その隠れ層を生成する重みが単語ごとの特徴ベクトルとなる。3 層の word2vec は深層ニューラルネットワーク (DNN) ではないが、テキストを DNN が解釈できる数値形式に変換するための前処理として使用されることが多い。

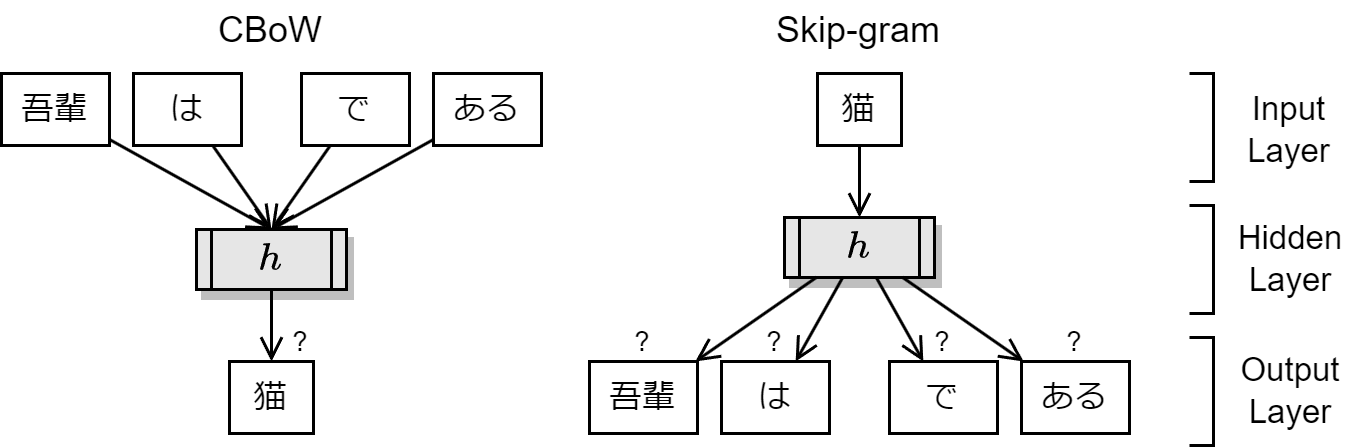
word2vec のアルゴリズムには CBoW (continuous bag of words) と Skip-gram の 2 種類がある。一連の単語シーケンスが与えられたとき、CBoW は単語の近傍 (文脈) から単語を予測するように学習する。Skip-gram は逆に単語からその近傍の単語を予測するように学習する。大規模なデータセットに対しては Skip-gram の方が正確な結果が得られる傾向にあることから Skip-gram がよく使用されている。

Fig 3 における Skip-gram の例では、事後確率 \(P(吾輩|猫)\), \(P(は|猫)\), \(P(で|猫)\), \(P(ある|猫)\) を予測するような学習を行ったとき、隠れ層の \(h\) が単語の特徴ベクトルとなる値を持つ。

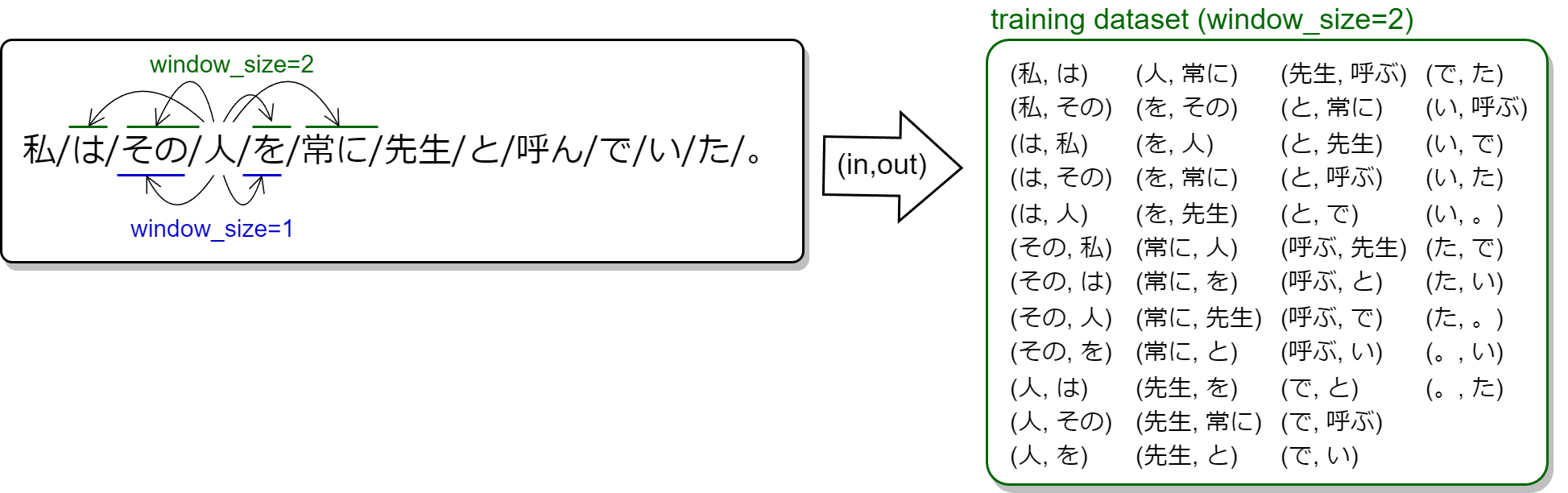
word2vec のニューラルネットワークには、位置 \(t\) の単語 \(x\) を入力としたとき、\(x\) の近傍の \(t \pm 1..c\) に位置する単語 \(y\) が最適な生起確率で出現するような学習データセットを作成する。近傍とはウィンドウサイズ \(c\) によって表される範囲である。Fig 4 に示すように、例えばウィンドウサイズに \(c=2\) を指定すると単語 \(x\) の前後 2 単語が近傍となる。

直感的には、例えば「レストラン」という単語の近傍には「ステーキ」や「スパゲティ」といった単語が含まれる可能性が高く、それらを特徴空間上の近い位置に配置することで料理という潜在的なクラスタを構成することができる。また逆に料理を表す単語の近傍に存在する「レストラン」「ダイナー」「バル」といった単語は飲食店という潜在的なクラスタとなる。

文を超える近傍は意味の関連が薄いため、文頭の前や句点の後には単語が存在しないものとして、文単位でデータセットを構築する。

入力層

大きさ \(V\) を持つコーパス内のすべての単語に \(i \in [0,V-1]\) 範囲のインデックスが割り当てられていると仮定する。それらの単語を表す値として、コーパスの大きさと等しい次元を持ち、単語インデックスに対応する位置が 1 で残りはすべて 0 の値を持つ単純なベクトルを想定する。例えばコーパス「吾輩/は/猫/で/ある/。」に含まれる各単語は以下のようなベクトルとして表すことができる: \[ {\scriptstyle \begin{eqnarray*} 吾輩 & = & (1, 0, 0, 0, 0, 0) \\ は & = & (0, 1, 0, 0, 0, 0) \\ 猫 & = & (0, 0, 1, 0, 0, 0) \\ で & = & (0, 0, 0, 1, 0, 0) \\ ある & = & (0, 0, 0, 0, 1, 0) \\ 。& = & (0, 0, 0, 0, 0, 1) \end{eqnarray*} } \] このような 1 つの要素のみが 1 となるベクトルをワンホットベクトル (one-hot vector) または 1-of-\(V\) と呼ぶ。ワンホットベクトルにより単語は固定長のベクトルとなるためニューラルネットワークの入出力層のニューロン数を決定することができる。

学習データセットの入力単語と出力単語のペア \((x,y)\) の集合を \(D\) とする。\(D\) の入力単語と出力単語をワンホットベクトルで表現した場合、入力と出力はそれぞれ同じ次元 \(|D| \times V\) を持つ行列として表すことができる。\[ {\scriptstyle \begin{equation} D= \left( \begin{array}{c} (吾輩,は) \\ (は,吾輩) \\ (は,猫) \\ (猫,は) \\ (猫,で) \\ (で,猫) \\ (で,ある) \\ (ある,で) \\ (ある,。) \\ (。,ある) \end{array} \right) \Rightarrow \left( \left( \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right), \left( \begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ \end{array} \right) \right) \label{example} \end{equation} } \] バッチ処理のために式 (\(\ref{example}\)) のような \(D\) の入出力行列ペアをバッチサイズ \(S=10000\) 程度の単語ペアに分割する。バッチサイズに分割された入力と出力の塊をそれぞれ \(S \times V\) 次元の行列 \(\vector{X},\vector{Y} \in \mathbb{R}^{S \times V}\) とする。

隠れ層

Skip-gram のケースではまず第一重み行列 \(\vector{W}_1 \in \mathbb{R}^{V \times N}\) を使って入力 \(\vector{X}\) を \(S \times N\) 次元の隠れ層 (または射影層) \(\vector{H}=\vector{X}\vector{W}_1 \in \mathbb{R}^{S \times N}\) に変換する。式 (\(\ref{hidden}\)) はある入力単語 \(\vector{x}_{i=0} \in \vector{X}\), \(V=6\), \(N=3\) のケースでの変換の例を表している: \[ \begin{equation} \vector{x}^6_0 \cdot \vector{W}^{6 \times 3}_1 = (1,0,0,0,0,0) \left( \begin{array}{ccc} w_{0,0} & w_{0,1} & w_{0,2} \\ \vdots \\ w_{5,0} & w_{5,1} & w_{5,2} \end{array} \right) = (w_{0,0}, w_{0,1}, w_{0,2}) = \vector{h}^3_0 \label{hidden} \end{equation} \] ワンホットベクトルに対する重み行列の適用は、単に重み行列の特定の行を選択しているに過ぎないことに注意。言い換えると第一重み行列 \(\vector{W}_1\) の各行は各単語に対応したベクトル値を取り出すためのルックアップテーブルと見なすことができる (入力単語のインデックス \(i\) に対するルックアップテーブルで代用することができる)。そして、最終的に学習の済んだ word2vec モデルの第一重み行列が分散表現となる。したがって隠れ層 \(\vector{h}\) の次元 \(N\) は特徴ベクトルサイズである。

出力層

次に第二重み行列 \(\vector{W}_2 \in \mathbb{R}^{N \times V}\) を用いて隠れ層 \(\vector{H}\) を \(S \times V\) 次元の行列 \(\vector{Y}' = \vector{H} \vector{W}_2 \in \mathbb{R}^{S \times V}\) に変換し、さらに Softmax 関数を使って各要素で総和が 1 となるような確率ベクトル \(\vector{Y}'_s\) へ正規化する。\[ \begin{equation} {\rm Softmax}(\vector{Y}') = \left( \begin{array}{c} (e^{y'_{0,0}},e^{y'_{0,1}},\ldots,e^{y'_{0,V-1}})/\sum_{k=0}^{V-1} e^{y'_{0,k}} \\ \vdots \\ (e^{y'_{S-1,0}},e^{y'_{S-1,1}},\ldots,e^{y'_{S-1,V-1}})/\sum_{k=0}^{V-1} e^{y'_{S-1,k}} \\ \end{array} \right) = \vector{Y}'_s \label{softmax} \end{equation} \] 現実の実装では Softmax 関数は計算コストが高いため階層的 Softmax が使用される。

バックプロパゲーション

モデルの重み \(\vector{W}_1\) と \(\vector{W}_2\) は乱数を初期値として構築する。そしてイテレーションごとに誤差に基づいた調整が行われる。まず式 (\(\ref{softmax}\)) で算出した実際の出力値 \(\vector{Y}'_s\) と想定する出力値 \(\vector{Y}\) との差 \(\vector{E}\) を算出する。\[ \begin{equation} \vector{E} = \vector{Y}'_s - \vector{Y} \in \mathbb{R}^{S \times V} \label{error} \end{equation} \] 式 (\(\ref{error}\)) に基づいて式 (\(\ref{backpropagation}\)) によってモデルの重み行列 \(\vector{W}_1\) と \(\vector{W}_2\) を調整する。ここで \(\alpha\) は調整をどれだけ強く反映させるかを示す学習率 (learning rate) である。\[ \begin{equation} \left\{ \begin{array}{l} \vector{W}'_1 = \vector{W}_1 - \alpha (\vector{X}^\mathsf{T} \cdot (\vector{E} \cdot \vector{W}_2^\mathsf{T})) \ \in \mathbb{R}^{V \times N}\\ \vector{W}'_2 = \vector{W}_2 - \alpha (\vector{H}^\mathsf{T} \cdot \vector{E}) \ \in \mathbb{R}^{N \times V} \end{array} \right. \label{backpropagation} \end{equation} \]

\(\vector{Y}\) も \(\vector{Y}'_s\) も離散確率分布を表していることから、式 (\(\ref{cross_entropy}\)) のようにそれぞれの交差エントロピーを求めることで、イテレーションごとに誤差が減少してゆく課程が分かる。\[ \begin{equation} H(\vector{Y}, \vector{Y}'_s) = - \sum_{S,V} \vector{Y} \log \vector{Y}'_s \label{cross_entropy} \end{equation} \]

結論

結果的に Skip-gram を適用した word2vec のニューラルネットワークの機能は Fig 5 のように表すことができる。

論文 [1] では \(V=783M\)、\(N=300\) を使った結果が示されている。単語のワンホットベクトルの大きさ、つまり入出力ベクトルの次元 \(V\) はコーパスに含まれる単語数であるため数万から数億に及ぶことがある。一方で、その特徴ベクトルとなる隠れ層 \(h\) の次元 \(N\) は数百から数千程度である。これは単語の特徴が次元圧縮されているとも考えることができる。つまり word2vec は DNN の Encoder-Decoder ネットワークで低次元の潜在表現を学習していることと同じ構造であることがうかがえる。

word2vec の利用

word2vec の簡単な試行は Python ライブラリの Gensim を利用することができる。

text8 データセット

text8 は Wikipedia から抽出しクレンジングしたデータの最初の 100MB を使用した試用目的のデータセットである。以下の例は text8 データセットを用いて 'king'-'man'+'woman'≃'queen' の例を演算している。

$ pip3 install gensim

Collecting gensim
  Downloading gensim-4.3.1-cp310-cp310-win_amd64.whl (24.0 MB)
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 24.0/24.0 MB 11.5 MB/s eta 0:00:00
Collecting scipy>=1.7.0
  Downloading scipy-1.11.2-cp310-cp310-win_amd64.whl (44.0 MB)
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 44.0/44.0 MB 9.9 MB/s eta 0:00:00
Collecting smart-open>=1.8.1
  Downloading smart_open-6.3.0-py3-none-any.whl (56 kB)
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 56.8/56.8 kB 3.1 MB/s eta 0:00:00
Collecting numpy>=1.18.5
  Downloading numpy-1.25.2-cp310-cp310-win_amd64.whl (15.6 MB)
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 15.6/15.6 MB 12.3 MB/s eta 0:00:00
Installing collected packages: smart-open, numpy, scipy, gensim
Successfully installed gensim-4.3.1 numpy-1.25.2 scipy-1.11.2 smart-open-6.3.0

$ cat w2v_text8.py

import os
import gensim.downloader as api
from gensim.models import Word2Vec

filename = "word2vec-text8.model"
if os.path.exists(filename):
  model = Word2Vec.load(filename)
else:
  dataset = api.load("text8")
  model = Word2Vec(dataset)
  model.save(filename)
print(model.wv.most_similar(positive=["king", "woman"], negative=["man"], topn=3))
print(model.wv.most_similar(positive=["washington", "japan"], negative=["us"], topn=3))

$ python3 w2v_text8.py

[==================================================] 100.0% 31.6/31.6MB downloaded
[('queen', 0.7043117880821228), ('throne', 0.6485360264778137), ('prince', 0.6437445878982544)]
[('shanghai', 0.6013388633728027), ('tokyo', 0.5882682800292969), ('china', 0.5333846807479858)]

上記のプログラムでは起動ごとのデータセットのダウンロードや学習時間を省略するために学習済みの word2vec モデルをローカルに保存している。

text8 より大きなデータセットとしては標準で wiki-english-20171001, patent-2017, quora-duplicate-question などを利用できる (利用可能な識別子は python -m gensim.downloader --info コマンド実行結果の corpora で確認できる)。

独自のデータセット

Gensim の Word2Vec を使用してユーザの保有する自然文データから word2vec モデルを構築することもできる。小規模な学習セットであれば構築時の sentences パラメータで指定できる。また一度にメモリ上にロードすることが現実的ではない大規模な学習セットに対しては、構築後のモデルに対して train() を使用して追加的に学習できる。

参照

1. Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean. Efficient Estimation of Word Representations in Vector Space (日本語). arXiv preprint arXiv:1301.3781, 2013.
2. Word2vec (Wikipedia)