指数平滑化法
定義と性質
指数平滑化法 (exponential smoothing) は時系列データを平滑化する代表的な時系列分析手法。観測値の中でより新しいデータに大きな重みを設定し、過去になるほど指数関数的に重みを減少させた期待値 (移動平均) を算出する。直近の観測値の変動に従属させたいような比較的短期間の期待値を決めるのに適している。
カルマンフィルター (Kalman filter)は重回帰モデルにおける時間に依存するパラメータ推定値を、次の従属変数が利用可能になった時に計算機により更新する方法である。指数平滑化法はカルマンフィルターに関係する繰り返し計算の単純な例と言える。
基本的な考え方
単純な指数平滑化法はある時点の期待値と実際の観測値の差から次の期待値を決定する。観測対象がランダムウォークを動きを見せる場合、指数平滑化法はそれに追従する変動を見せる。
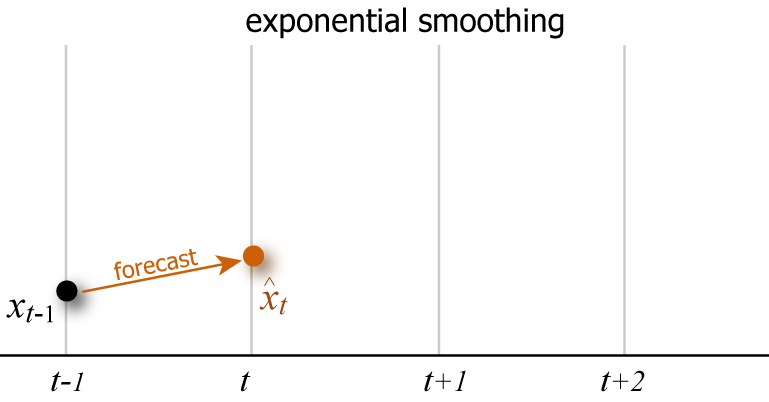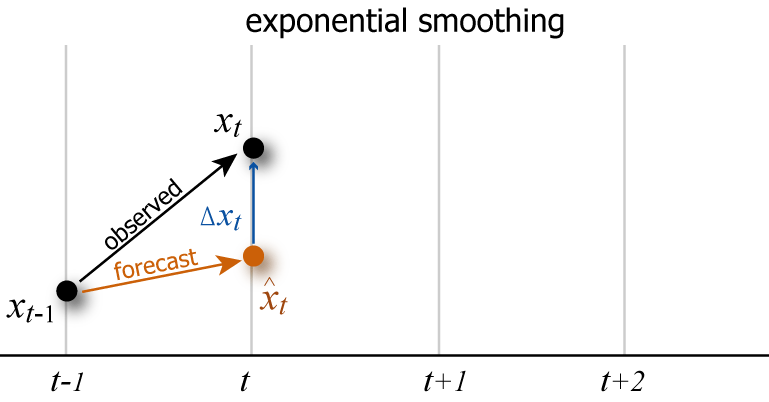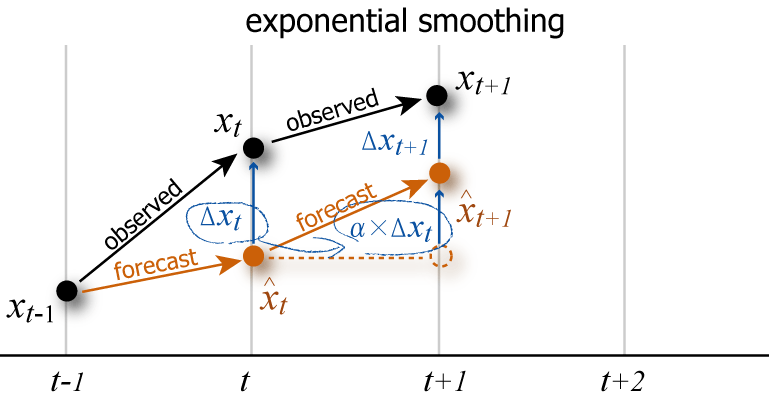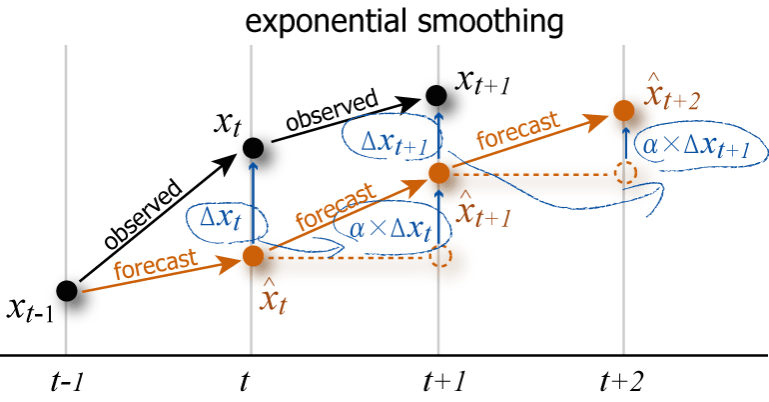
観測値を \((x_0, x_1, \ldots, x_n)\) とした場合、ある時点 \(t\) の期待値 \(\hat{x}_t\) は「前回の観測値 \(x_{t-1}\) がその期待値 \(\hat{x}_{t-1}\) からどれだけ離れていたか」に係数 \(\alpha\) を掛けた修正値を前回の期待値に加算する。\[ \begin{equation} \left\{ \begin{array}{rcll} \hat{x}_1 & = & x_0 & (t = 1)\\ \hat{x}_t & = & \hat{x}_{t-1} + \alpha (x_{t-1} - \hat{x}_{t-1}) \\ & = & \alpha x_{t-1} + (1 - \alpha) \hat{x}_{t-1} \ \ & (t = 2, 3, \ldots, n) \end{array} \right. \label{single_exponential_smoothing} \end{equation} \]
指数平滑化法は新しい期待値を算出するために直前の観測値と期待値のみを使えば良く \(t\) が非常に大きくなるような時系列では計算効率が良い。
この方法はトレンド (上昇傾向/下降傾向) も季節変動 (周期性) も持たない時系列に対する予想値であり、長期に渡って時系列が存在していると仮定されている。トレンドと季節変動を持った時系列に対しては Holt-Winters 法を使用する。
観測値との乖離
時系列予測において予測モデルが実際に観測される観測値と適合しているかの指標は時系列の全体に対して誤差の二乗和 (SSE; Sum of Squared Errors) を取ることによって表すことができる。\[ \begin{equation} {\rm SSE} = \sum_{i=1}^n (x_i - \hat{x}_i)^2 \label{sse} \end{equation} \] または \(x\) と次元を合わせるために平方根を取った平均二乗誤差 (MSE) でも表すことができる。
平滑化定数の性質
平滑化定数 \(\alpha\) は 1 に近づくと直近の観測値の影響が強くなり 0 に近づくと過去の観測値の影響が強くなる。特に \(\alpha=1\) では次の期待値として直前の観測値を採用する。また \(\alpha=0\) では初期値 \(x_0\) から変化しない。\[ \left\{ \begin{array}{ll} \hat{x}_t = \hat{x}_{t-1} = \ldots = \hat{x}_1 = x_0 \ \ & (\alpha = 0) \\ \hat{x}_t = x_{t-1} & (\alpha = 1) \end{array} \right. \]
\(\alpha\) は一般的に既に観測されている時系列データに対して SSE (\(\ref{sse}\)) が最小となるような \(0 \lt \alpha \lt 1\) 範囲の値を選択する。ただし、トレンドや季節変動を考慮しない単純な指数平滑では \(\alpha \simeq 1\) で SSE が最小となるためこの選択には意味がない (後述のシミュレーションで試すと良い)。
シミュレーション (ランダムウォーク/ホワイトノイズ)
以下の例は正規乱数またはホワイトノイズ (正規乱数) を使ったランダムウォークを観測値として指数平滑化法で期待値を算出する。スライダーで平滑定数 \(\alpha\) を調整して双方の乖離を見ることができる。
| 観測値平均 \(\bar{x}\) | 0 |
|---|---|
| 観測数 \(n\) | 0 |
| 平滑定数 \(\alpha\) | 0 |
| SSE | 0 |