Holt-Winters 法
 定義と性質
定義と性質
ホルト-ウィンターズ法 (Holt-Winters method) は指数平滑化法における時系列の変動にトレンドと季節変動を追加し、それぞれの指数平滑の重ね合わせを期待値として算出する方法。このため 3 重指数平滑化法 (triple exponential smoothing) とも呼ばれる。トレンドは時系列の上昇傾向または下降傾向を示すものであり、季節変動は一定の周期で繰り替えされる時系列の変化を表している。
ホルト-ウィンターズ法は季節変動が必要である。株価のように明確な季節変動 (一定の周期変動) がない時系列を扱うことはできない。
 レベルとトレンド
レベルとトレンド
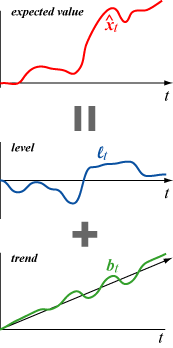
指数平滑化法では以下の式で期待値を算出していた。\[ \begin{equation} \left\{ \begin{array}{rcll} \hat{x}_1 & = & x_0 & (t = 1)\\ \hat{x}_t & = & \hat{x}_{t-1} + \alpha (x_{t-1} - \hat{x}_{t-1}) \ \ & (t = 2, 3, \ldots, n) \end{array} \right. \label{single_exponential_smoothing} \end{equation} \] この \(\hat{x}\) をトレンドを考慮しない期待値と考え Holt-Winters 法ではレベル \(\ell_t\) と再定義する。
トレンド (trend) は長期的な上昇または下降を示す傾き (slope) である。期待値 \(\hat{x}\) の変動をレベル \(\ell\) とトレンド \(b\) の重ね合わせと考える。\[ \begin{equation} \hat{x}_{t+1} = \ell_t + b_t \label{double_exponential_smoothing} \end{equation} \]
レベル \(\ell_t\) は式 (\(\ref{single_exponential_smoothing}\)) と (\(\ref{double_exponential_smoothing}\)) より以下のように表すことができる。\[ \begin{align} \ell_t & = \alpha x_t + (1-\alpha) \hat{x}_t \nonumber \\ & = \alpha x_t + (1-\alpha)(\ell_{t-1} + b_{t-1}) \label{des_level}\\ \end{align} \]
レベルの傾きは \(\frac{\Delta \ell}{\Delta t}\) で表されるが、等間隔の時系列データを扱う上では \(\Delta t=1\) とし差分 \(\ell_t - \ell_{t-1}\) を傾きと考えて差し支えない。
トレンド \(b_t\) は時点 \(t\) にごとに変動するレベル \(\ell_t\) の傾き (差分) の期待値を表している。従って、その移動平均も指数平滑の式 (\(\ref{single_exponential_smoothing}\)) を適用して以下のように表すことができる。\[ \begin{equation} b_x = \beta (\ell_t-\ell_{t-1}) + (1-\beta)b_{x-1} \label{des_trend} \end{equation} \] 定数 \(\beta\) はトレンド因子またはコヒーレンスと呼ばれる。
レベルとトレンドを使った平滑化方法は 2 重指数平滑 (double exponential smoothing) である。周期的な季節変動がなく長期的な上昇または下降傾向をもつモデルの移動平均として使用することができる。Holt-Winters 法はさらに季節変動を使用する。
 季節変動
季節変動
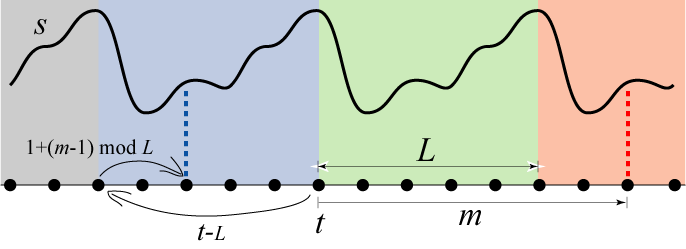
時系列が一定周期 \(L\) で反復する変動を見せるとき、時系列は季節変動 (seasonality) を持つ。季節変動を想定する時系列ではレベル \(\ell\) とトレンド \(b\) に加えて季節成分 \(s\) が一定の周期で加えられる。
例えば \(s_{t-L}\) は前周期の \(t\) と同じ時点の季節成分を表している。季節成分は1周期前、2周期前、... の同じステップから指数関数的に平坦化される。
観測済みの時点 \(t\) から \(m\) ステップ未来の期待値 \(\hat{x}_{t+m}\) はレベル \(\ell\)、トレンド \(b\)、季節成分 \(s\) を重ね合わせて以下のように表される。\[ \hat{x}_{t+m} = \ell_t + mb_t + s_{t-L+1+(m-1) \mod L} \]
レベル \(\ell_t\) に \(m\) 倍したトレンド \(b_t\) を加算するのは単純な線形方程式 \(y = ax + b\) である。Holt-Winters 法はさらに前サイクルの \(m\) のステップに相当する季節成分を加算する。季節成分 \(s\) のインデックスは若干複雑だが、これは \(t\) の直近のサイクル内で時点 \(t+m\) と同じステップ位置を意味している。
レベル \(\ell_t\) はトレンドでの式 (\(\ref{des_level}\)) における観測値 \(x_t\) がレベルと季節成分によって構成されていると考えて差を使用する。\[ \ell_t = \alpha (x_t - s_{t-L}) + (1-\alpha)(\ell_{t-1} + b_{t-1}) \]
トレンド \(b_t\) は傾きの期待値であり、季節成分による変動を含んでいないことから式 (\(\ref{des_trend}\)) がそのまま適用される。\[ b_x = \beta (\ell_t-\ell_{t-1}) + (1-\beta)b_{x-1} \]
季節成分 \(s\) も前の周期の同じステップからの変動という形で指数平滑を適用する。レベルと同様に観測値 \(x_t\) とレベルの差を使用する。\[ s_t = \gamma (x_t - \ell_t) + (1-\gamma)s_{t-L} \]
 初期値
初期値
各成分の初期値を確定する理論はないが、一般的にトレンドの初期値 \(b_0\) は最初の周期と次の周期を使用して 1 ステップごとの傾き平均の周期の平均を使用する。\[ b_0 = \frac{1}{L} \left(\frac{x_{L+1}-x_1}{L} + \frac{x_{L+2}-x_2}{L} + \cdots + \frac{x_{L+L}-x_L}{L}\right) \] この方法での初期値 \(b_0\) の算出は少なくとも 2 周期が観測済みでなければならない。
季節成分の初期値 \(s_0\) は少々複雑。観測されている時系列の有効な周期数を \(n_s = \lfloor \frac{n}{L} \rfloor\) としたとき、各周期における観測値の平均は以下のように表される。\[ \begin{align*} \bar{\vector{\ell}} & = (\bar{\ell}_1,\bar{\ell}_2, \ldots, \bar{\ell}_{n_s}) \\ \bar{\ell}_j & = \frac{1}{L} \sum_{i=1}^{L} x_{j \times L + i - 1} \end{align*} \]
1 から \(L\) までのステップごとに全周期の該当ステップと平均の差の平均を季節成分 \(s\) の初期値 \(s_0\) とする。\[ \begin{align*} \vector{s}_0 & = (s_{0,1}, s_{0,2}, \ldots, s_{0,n_s}) \\ s_{0,i} & = \frac{1}{n_s} \sum_{j=1}^{n_s} (x_{j \times L + i - 1} - \bar{\ell}_j) \end{align*} \] この方法での既設成分 \(s_0\) の算出は少なくとも 1 周期が観測済みでなければならない。
定数 \(\alpha\), \(\beta\), \(\gamma\) は一般的に SSE (\(\ref{sse}\)) を最小にする最適化問題として Nelder–Mead method で求めることができる。ただし、観測済みの時系列データが少なく計算量を気にしないのであればヒューリスティックに 1/100 程度の刻みで最小値を求めても良い (計算量は刻み数の3乗となる)。
 シミュレーション (東京都の気温予測)
シミュレーション (東京都の気温予測)
以下は気象庁東京 - 日平均気温の月平均値(℃) より東京都心部の月ごとの平均気温推移を抜粋したもの。1875年6月~2018年1月のデータから2年先の平均気温を予測している。
月の平均気温は \(\alpha \simeq 0\) (最初期と同程度のレベル)、\(\gamma \simeq 1\) (前年と同程度の形) 付近で SSE が小さくなる (周期によって大きな変動がないため?)。
 アプリケーション
アプリケーション
以下のアプリケーションはタブ区切りの時系列データ \((t, x)\) または1次元の系列 \(\vector{x}\) を入力すると 1/20 区切りに SSE を求め最適なパラメータでグラフに描画する。
デフォルトで使用しているデータは気象庁のサイトより得た二酸化炭素濃度の月平均値の 2005年1月~2017年5月のデータである。