マルコフ連鎖モンテカルロ法
定義と特徴
マルコフ連鎖モンテカルロ法 (Markov chain Monte Carlo methods; MCMC 法) は確率分布から疑似乱数サンプリングを行うためのアルゴリズム。ある時点の状態 \(x^{(t)}\) からランダムに採択した次の状態 \(x^{(t+1)}\) へ確率付きで移動することから "マルコフ連鎖", "モンテカルロ法" の名前で呼ばれる。
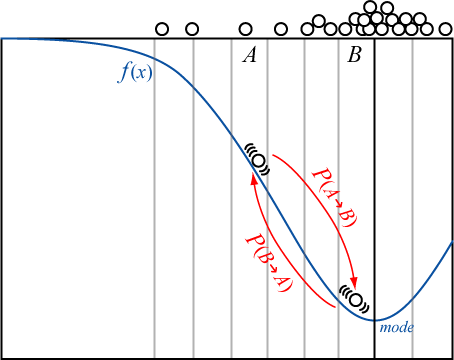
MCMC 法はどのような確率密度関数でもそれに比例する分布 \(P(x)\) さえ分かれば分布に従うサンプル (標本) を得ることができる。
用途
任意の分布に従う疑似乱数発生器として使用することができる。ただし burn-in 期間を注意深く決めなければならない。また直前のサンプルに強く関係しているため \(n\) ステップごとに採択するなどの考慮が必要である。
ベイズ推定では事後確率分布の特定に使用される。事後確率は比例する分布は分かっても正規化項 (エビデンス) を解析的に求めることが困難であることが多い。MCMC 法を用いて分布から得られた標本サンプルからパラメータを求める目的で使用される。
多次元 (多変量分布) であってもサンプリングが可能であることから多重モンテカルロ積分として使用される。
Burn-in期間
初期状態を任意にとるのであれば、ランダムウォークが分布の特徴に乗るまでの burn-in 期間に採集したサンプルはノイズである。このためサンプリング初期のサンプルは破棄する必要があるが、どの程度を破棄すればよいかは分布の複雑さや初期状態に依存する。一般的な目安は概ね 1000 程度である。
詳細釣り合い条件
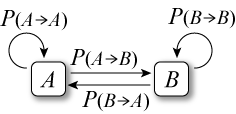
状態 \(A\) から \(B\) へ遷移する確率を \(P(A\to B)\)、\(B\) から \(A\) へ遷移する確率を \(P(B\to A)\) とする。
以下の詳細釣り合い条件 (detailed condition of equilibrium) を満たす確率分布において状態 \(A\), \(B\) 間を確率付きのランダムウォークで移動するとき、どちらの状態にいるかの確率はステップ数が十分に大きくなれば平衡状態 (不変分布) に収束する。\[ P_A P(A\to B) = P_B P(B\to A) \]
以下に説明する M-H アルゴリズムやギブスサンプリングが詳細釣り合い条件を満たしている証明は参考文献 3, 4 などを参照。
メトロポリス-ヘイスティングアルゴリズム
メトロポリス-ヘイスティングアルゴリズム (Metropolis-Hastings algorithm; M-H アルゴリズム) は MCMC 法の代表的なアルゴリズムである。以下の手順で目標分布 \(P\) に従う状態 \(x_0, x_1, \ldots\) をサンプリングする。
初期状態 \(\vector{x}_0\) を決定する。以下 2. 以降を繰り返す。
次の状態 \(\vector{x}_{t+1}\) の候補 \(\vector{x}'\) を現在の状態 \(\vector{x}_t\) から以下の式で導出する。\( Q(\vector{x}'|\vector{x}_t)\) は状態 \(\vector{x}_t\) から \(\vector{x}'\) を決定するための提案分布 (proposal distribution) であり、\(\vector{\epsilon}\) はその分布に従う乱数である。\[ \vector{x}' = \vector{x}_t + \vector{\epsilon}, \ \ \vector{\epsilon} \sim Q(\vector{x}'|\vector{x}_t) \]
提案分布はサンプリングが収束する速さに関係する。目標分布に比べて提案分布の広がりが小さいと 1 ステップの移動距離も短くなり分布の特定に必要な空間を網羅するのに多数の試行が必要になる。逆に広がりが大きいと 1 ステップの移動距離が大きくなり棄却率が高くなる。
提案分布が対称 \(Q(y|x)=Q(x|y)\) であれば 3. の採択確率で考慮する必要がないことからしばしば多変量正規分布 \({\rm Norm}(\vector{0},\sigma^2)\) が使用される。
\(\frac{\partial\log P(\vector{x})}{\partial\vector{x}}\) を求めることが可能であれば文献のランジェヴァン連鎖 (Langevin chain) によって最頻値近くのサンプル率を高めることができる。
状態候補 \(\vector{x}'\) を採択するか棄却するかを決定する採択確率 (acceptance probability) \(\phi\) を以下のように導出する。\[ \phi(\vector{x}_t \to \vector{x}') = {\rm min}\left\{1, \frac{P(\vector{x}')}{P(\vector{x}_t)}\frac{Q(\vector{x}_t|\vector{x}')}{Q(\vector{x}'|\vector{x}_t)}\right\} \]
採択確率は移動先の確率が同じか高ければ必ず移動し、低ければ \(0 \leq p \lt 1\) の確率で移動するか棄却するかを決定する (棄却された場合は同じ状態が連続してサンプリングされる)。
採択確率は比であることから目標分布が必ずしも正規化されている必要はないことが分かる。
一様乱数 \(u \in [0, 1]\) を \(\phi\) と比較し \(\vector{x}'\) を次の状態として採択するか棄却するかを決定する。\[ \vector{x}_{t+1} = \left\{ \begin{array}{ll} \vector{x}' & (u \leq \phi)\\ \vector{x}_t & (otherwise) \end{array} \right. \]
M-H アルゴリズムは遷移先として選んだ方向に一つでも低確率となる次元を含むと棄却されやすい傾向がある。しかし高次元のランダムウォークにおいて全ての次元で確率が高くなる方向を選ぶことはまれである。このため分布が高次元になると棄却率が上がりある状態から別の状態への遷移が渋くなって収束速度は悪化する。
メトロポリス法の可視化
以下のデモは 2 次元正規分布の目標分布をメトロポリス法でサンプリングし、その出現頻度をヒートマップで表している。
| \(t=\) | 0 |
| 状態 \(\vector{x}_t=\) | (0,0) |
| 標本平均 \((\mu_x,\mu_y)=\) | (0,0) |
| 標本共分散 \((\sigma^2_x,\sigma^2_y,\sigma_x\sigma_y)=\) | (0,0,0) |
目標分布: 2次元正規分布 \({\rm Norm}(\vector{\mu},\Sigma)\) \[ \begin{eqnarray} \vector{\mu} & = & (\mu_x,\mu_y) & = & (0,0) \nonumber\\ \Sigma & = & \left(\begin{array}{cc}\sigma^2_x&\sigma_x\sigma_y\\\sigma_y\sigma_x&\sigma^2_y\end{array}\right) & = & \left(\begin{array}{cc}0.25&0.25\\0.25&0.25\end{array}\right) \nonumber \end{eqnarray} \]
ギブスサンプリング
参考文献
- 古澄英男 (2008), "マルコフ連鎖モンテカルロ法入門", PDF
- 一石賢 (2016), "意味がわかるベイズ統計学", ベレ出版, ISBN-978-4860644659
- 豊田秀樹 (2008), "マルコフ連鎖モンテカルロ法 (統計ライブラリー)", 朝倉書店
- Olle H¨aggstr¨om (2017), "やさしいMCMC入門: 有限マルコフ連鎖とアルゴリズム", 共立出版