\( \def\vector#1{\boldsymbol{#1}} \)

疑似乱数サンプリング

2017年10月10日

疑似乱数サンプリング (pseudo-random number sampling) は与えられた確率分布に従う擬似乱数を生成する数値的手法。一般に一様乱数 \(u\) を利用して一様ではない分布のサンプリングを行う。

サンプリングアルゴリズム
分布ごとの生成方法
参考文献

サンプリングアルゴリズム

逆関数法

ある確率密度関数 \(f(x)\) に対して、その累積分布関数 (CDF; cumulative distribution function) の逆関数 \(F^{-1}(x)\) に一様乱数 \(0 \leq r \lt 1\) を適用することで分布 \(f\) に従う乱数を解析的に得ることができる。この手法を逆関数法 (inverse transform sampling) または逆確率積分変換 (inverse probability integral transformation) と呼ぶ。

ここで累積分布関数は以下の不定積分で表される。\[ F(x) = \int_{-\infty}^x f(t) dt \]

確率密度関数 \(f(x)\) の全域での積分値が 1 であることから、累積分布関数の逆数 \(F^{-1}(x)\) は \(x \in (0, 1)\) の定義域を持つ。\((0, 1)\) の一様乱数を \(F^{-1}(x)\) に適用することで確率密度関数 \(f(x)\) に従う乱数を得ることができる。

ただし、累積分布関数の逆関数を解析的に求めることは難しい場合が多く、また必ずしも高速な式が得られるとは限らない。逆関数を解析的に求めることのできる累積分布関数 \(F(x)\) は以下のものが挙げられる。

指数分布	\(F(x) = 1 - e^{-1}, \ \ x \geq 0\)
ワイブル分布	\(F(x) = 1 - e^{-x^a}, \ \ x \geq 0\)
ロジスティック分布	\(F(x) = \frac{1}{1+e^{-x}}, \ \ -\infty \lt x \lt \infty\)
コーシー分布	\(F(x) = \frac{1}{2} + \frac{1}{\pi} \tan^{-1}x, \ \ -\infty \lt x \lt \infty\)

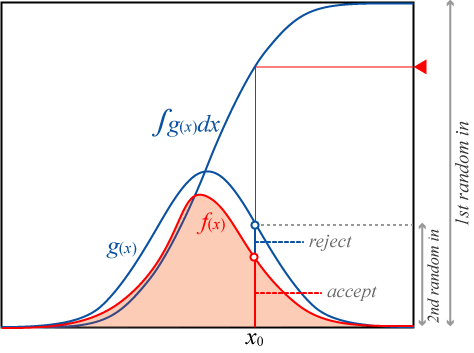
棄却サンプリング法

棄却サンプリング (rejection sampling) はモンテカルロ法を用いて分布 \(f(x)\) に従うサンプル (乱数) \(x\) を決定する方法である。

acceptance-rejection モンテカルロ法

分布 \(f(x)\) が有限の定義域 \(x\in[x_0,x_1]\) を持つとき、分布の最大値 \(y_1\) の範囲でモンテカルロ法を用いて乱数を生成することができる [3]。この方法は acceptance-rejection モンテカルロ法または選択棄却法と呼ばれる。

一様乱数 \(x\) を分布 \(f\) の定義域 \([x_0, x_1]\) で決定する。
一様乱数 \(y\) を分布 \(f\) の値域 \([0, y_1]\) で決定する
\(y \lt f(x)\) であれば \(x\) を \(f(x)\) に従う乱数として採用する。そうでなければ棄却しやり直す。

この方法は (理論上) 任意の分布に従う乱数を生成することができる。しかし、定義域の一方が \(\pm\infty\) かそれに近い大きな数をとる分布は棄却数が膨大になるため現実的ではない。ベータ分布のように定義域が限定的であり、後述の比較関数を用意する手間を省く簡易的な手段である。

比較関数を使った方法

ここでモンテカルロ法の棄却数を効率的に削減するために分布 \(f(x)\) のすべての定義域で \(g(x) \gt f(x)\) となるような比較関数 (comparison function) または提案関数 (proposal function) と呼ばれる関数を導入する。

比較関数の種類は任意で良いが、前述の逆変換法を使用するため不定積分と逆関数が解析的に求められる関数を選ぶ必要がある。

比較関数 \(g(x)\) の不定積分逆関数を \(G^{-1}(x)\)、その最大値を \(R\) としたとき、比較関数を使った棄却サンプリングは以下の手順で行われる。

一様乱数 \(u\) を \(0 \leq u \lt R\) の範囲で生成する。
乱数の候補 \(x = G^{-1}(u)\) を求める。
一様乱数 \(y\) を \(0 \leq y \lt g(x)\) の範囲で生成する。
\(y \lt f(x)\) であれば \(x\) を \(f\) に従う乱数として採用する。そうでなければ棄却しやり直す。

3-4 は \(u\in[0,1)\) の乱数を生成して \(u\lt\frac{f(x)}{g(x)}\) を評価しても良い。

棄却される点の割合は比較関数 \(g(x)\) の面積と分布 \(f(x)\) の面積 (\(f\) が確率密度関数であれば1) の比に依存する。\(f(x)\) と \(g(x)\) の一部分に大きな乖離があったとしても全体としての面積比が大きくなければ問題ない。

比較関数を使った棄却サンプリングは \(f(x)\) の定義域が \(x\in[-\infty,\infty]\) であっても有効に機能する。ただし、対象とする分布ごとに適切な比較関数を選択しなければならない。

比較関数を使った棄却サンプリングは 1 度の算出に 2 つの一様乱数と \(f(x)\), \(g(x)\), \(G^{-1}(x)\) の算出が必要な上に棄却率がゼロではないことから、多くの場合、処理の効率は逆変換法に劣る。また棄却の最大回数が想定できないため、応答速度が求められるリアルタイム処理には次のような考慮が必要である。

棄却の上限回数やタイムアウトを設けてエラーにする。
事前に計算してプールする。

CPU コア数に余裕があれば棄却を見込んで 2-3 スレッドで投機的に実行しても良いだろう。

def rejection(f:(Double)=>Double, g:(Double)=>Double, gcinv:(Double)=>Double, r:Double):Double = {
  @tailrec
  def _rand():Double = {
    val x = gcinv(math.random() * r)
    val y = math.random() * g(x)
    if(y >= f(x)) _rand() else x
  }
  _rand()
}

適応 Squeezed 棄却サンプリング

適応絞り込み棄却サンプリング (adaptive squeezed rejection sampling) は棄却サンプリングでの効率を高めるために目標分布と提案分布の下に絞り込み関数 (squeeze function) を導入する。この関数によりサンプルが棄却される確率を減らし計算効率が向上する。適応スクイーズド棄却サンプリングは、目的分布から点を抽出する方法であり、スクイーズド棄却サンプリングのための自動エンベロープ生成戦略を利用することで、棄却サンプリングよりも一歩進んだ方法である。スクイージング棄却サンプリングは、単に提案密度を用いてサンプリングする方法で、棄却サンプリングと似ている（Cheng et al.2015）。ただし、この場合、1 つではなく 2 つの提案分布が使われる。棄却サンプリングは、スクイーズ棄却サンプリングの欠点を補うために改良されたサンプリング手法である。

マルコフ連鎖モンテカルロ法

マルコフ連鎖モンテカルロ法参照。

分布ごとの生成方法

指数乱数

指数分布 (exponential distribution) は連続する 2 つのイベント間の時間をモデル化するために使われる連続確率分布である。ランダムに起きる事故や故障のある発生時刻を \(t\) とし、次の発生時刻を \(t + \delta\) としたとき、\(\delta\) は指数分布に従う。なお、ある期間内でのそのようなイベントの発生回数はポアソン分布に従う。

指数分布は正のパラメータ \(\lambda\) に対して以下の確率密度関数、累積分布関数を持つ。\[ \begin{align*} f(x; \lambda) & = \left\{ \begin{array}{ll} \lambda e^{-\lambda x} & x \geq 0 \\ 0 & x \lt 0 \end{array} \right. \\ F(x; \lambda) & = \left\{ \begin{array}{ll} 1-e^{-\lambda x} & x \geq 0 \\ 0 & x \lt 0 \end{array} \right. \end{align*} \]

指数分布の累積分布関数は逆関数を求めることができる。\(x \geq 0\) の範囲で逆関数を求めると: \[ F^{-1}(x;\lambda) = -\frac{\log (1-x)}{\lambda} \]

また \(x\) は \(0 \leq x \leq 1\) の一様乱数であることから \(1-x\) は \(x\) と置くことができる。\[ F^{-1}(x;\lambda) = -\frac{\log x}{\lambda} \] したがって、\(0 \leq x \leq 1\) となるような一様乱数 x から指数分布に従う乱数を得るコードは次のように書くことができる。

def exponentialInverseCDF(lambda:Double)(x:Double):Double = {
  - math.log(x) / lambda
}

以下のグラフは \(\lambda = 1\) とした時の累積指数分布逆関数と、一様乱数を用いて実際にその関数からサンプリングしたヒストグラムである。

正規乱数 (ガウス乱数)

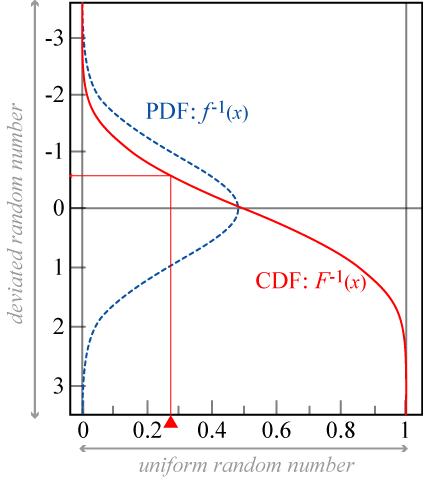
標準正規分布の累積分布逆関数は解析的に求めることはできないが、いくつかの近似方が提案されている。例えば以下の山内の近似では相対誤差が \(4.9\times 10^{-4}\) 以下で求めることができる。

\[ \begin{align*} F^{-1}(x) & = \left\{ \begin{array}{ll} -w, & 0 \lt x \lt 0.5 \\ +w, & 0.5 \leq x \lt 1 \end{array} \right. \\ w & = \sqrt{z\left(2.0611786-\frac{5.7262204}{z+11.640595}\right)} \\ z & = -\log \left\{4x(1-x)\right\} \end{align*} \]

def normalInverseCDF(x:Double):Double = {
  val z = - math.log(4 * x * (1 - x))
  val w = math.sqrt(z * (2.0611786 - 5.7262204 / (z + 11.640595)))
  if(x < 0.5) -w else w
}

以下のグラフは定義域 \(0 \leq x \lt 1\) での normalInverseCDF() のプロットと、一様乱数から得られた正規乱数のヒストグラムである。

そのほかにはボックス-ミュラー法が有名。

ガンマ乱数

ポアソン乱数

二項乱数

参考文献

Pseudo-random number sampling (Wikipedia)
逆関数法 (Wikipedia)
John von Neumann. Various techniques used in connection with random digits. Collected Works, 1963, 5: 768-770.