最小経路問題

2018年2月20日 #graphtheory

概要

重み付きグラフ上のある頂点 \(s\) から別の頂点 \(t\) まで到達する経路の中で最もコストの低い経路を求める問題 (重みなしグラフの場合は各辺の重みを 1 とする)。最小シュタイナー木問題において 2 点を使った最小コストの部分グラフを作成することと同じ。

概要
アルゴリズム
1. ダイクストラ法
2. ワーシャル・フロイド法
参考文献

アルゴリズム

ダイクストラ法

ダイクストラ (Dijkstra) のアルゴリズムは、ある小さな頂点集合 \(L\) から開始し、その集合内での各頂点の距離を求め、集合に含まれる頂点を少しずつ大きくしてゆく方法。ある頂点からそれ以外のすべての頂点の最短経路を求める方法としても利用できる。

以下の手順で頂点 \(s\) から \(t\) に向かって最短経路を求める。

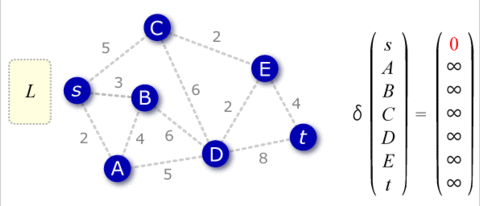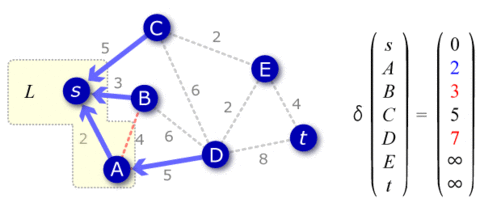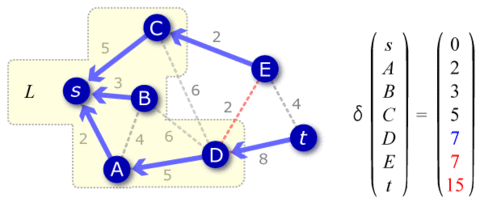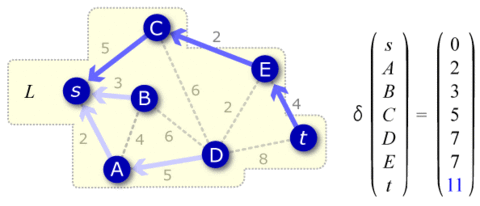
初期状態 \(L = \emptyset\), \(\delta(s) = 0\), 任意の頂点 \(v \neq s\) について \(\delta(v) = \infty\) から開始する。
\(L\) に \(s\) を加え、\(s\) に隣接している各頂点 \(v\) に対して距離 \(\delta(v) = d(s,v)\) を設定する。また \(v\) のポインタを \(s\) に設定する。
まだ \(L\) に含まれていない頂点の中で \(\delta(v')\) が最も小さい \(v'\) (複数存在する場合は任意の一つ) を \(L\) に加える。
\(L\) に加えた \(v'\) に隣接する、まだ \(L\) に含まれていない全ての頂点に対して \(\delta(u) = \min \left\{\delta(u), \delta(v') + d(v',u)\right\}\) を設定する。このとき、\(\delta(u)\) に変更があった場合はポインタの先を \(v'\) に付け替える。
\(t\) が \(L\) に含まれるまで 3-4 ステップを繰り返す。
\(t\) からポインタを遡って \(s\) に到達する経路が距離 \(\delta(t)\) を持つ \(s\)-\(t\) 最小経路である。

Figure 1. Dijkstra's Algorithm

グラフに含まれる頂点の数を \(n\) としたとき、上記の操作を最大 \(n\) 回繰り返せば全ての頂点が \(L\) に入り必ず \(t\) に到達することからこのアルゴリズムの計算量は \(O(n)\) である。また \(t\) を特定せず全ての頂点が \(L\) に含まれたとき、任意の \(v\) に対する \(\delta(v)\) とポインタは \(s\) からの最短距離とその経路を表している。