最小全域木問題
 概要
概要
いくつかの頂点と、各頂点の間をつなげるコスト (辺の重み) が定義されており、最も小さいコストですべての頂点をつなぐ最適化問題。コストは 0 より大きく接続不能 (つまりコスト \(\infty\)) も取り得る。すべての頂点がつながることから連結グラフでなければならず、また閉路はいずれか 1 本分の辺のコストが無駄であることから存在しない。従ってこのようなグラフは必ず木になり最小全域木 (minimum pinning tree) と呼ばれる。
 最小シュタイナー木問題
最小シュタイナー木問題
無向グラフ \(G = (V, E)\) における頂点の部分集合を \(T \subseteq V\) としたとき、\(T\) に含まれるすべての頂点をつなげた木をシュタイナー木 (Steiner tree) と呼ぶ。特に重み付けグラフにおいて最も小さなコストでシュタイナー木を作成する問題を最小シュタイナー木問題 (minimum Steiner tree problem) と呼ぶ。
\(T = V\) の場合は全域木と同じであるため明らかに最小全体木問題と等価である。また \(T\) に含まれる長点数が 2 の場合は最小経路問題と等価である。最小シュタイナー木問題は NP 困難であるため解くことは容易ではない。
 アルゴリズム
アルゴリズム
 クラスカル法
クラスカル法
クラスカル法 (Kruskal's algorithm) は閉路にならない最小コストの辺を選んでゆく操作をすべての頂点が接続されるまで繰り返す。疎集合データ構造 (disjoint-set data structure) の Union-Find アルゴリズムの適用例として知られている。この方法で最小全域木となる証明はP.27参照。
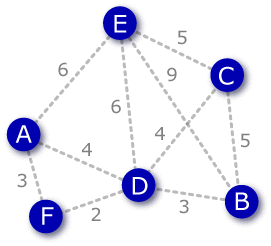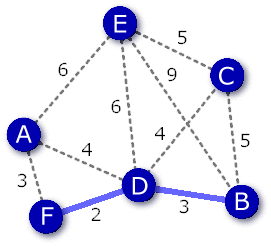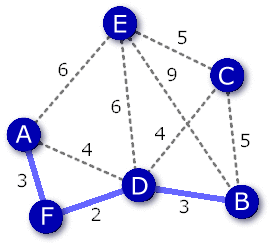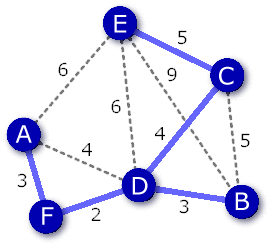
- 最初に最小コスト2の辺(D,F)をつなげる。
- 次に最小コスト3の辺(B,D),(A,F)のどちらを選んでも良いがここでは(B,D)をつなげる。
- 次の最小コスト3の辺(A,F)をつなげる。
- 次に最小コスト4の辺(A,D),(C,D)だが(A,D)は閉路となるため(C,D)をつなげる。
- 次に最小コスト5の辺(B,C),(C,E)だが(B,C)は閉路となるため(C,E)をつなげる。
閉路になるかは接続しようとしている辺の両端が既に選択されているかで判定ができる。全ての頂点と辺が記憶領域に乗る規模の一般的なグラフであれば、最初に全ての辺をソートし重みの低い順に閉路になるかどうかを評価してゆけば良いので実装は容易である。
 プリム法
プリム法
プリム法 (Prim algorithm) は連結部分グラフに対してコストが最小になる方向に拡大してゆく操作を全体が連結グラフとなるまで繰り返すアルゴリズム。最初に任意の頂点を選択し、最もコストの低い辺を選んで接続する。できあがった部分グラフ以外の頂点とを結ぶ最もコストの低い辺を選択する。この操作をすべての頂点が接続するまで繰り返す。
既に選択されている頂点とまだ選択されていない頂点を接続するためプリム法で閉路ができることはない。以下は適当な重み付き隣接行列を定義するとプリム法で最小全域木を作成する。
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 1 | 1 | 1 | 1 | 1 |
| B | 0 | 1 | 1 | 1 | 1 | |
| C | 0 | 1 | 1 | 1 | ||
| D | 0 | 1 | 1 | |||
| E | 0 | 1 | ||||
| F | 0 |
\(\sum w\) = 0
クラスカル法と比べて大きな違いがあるわけではないが、クラスカル法がグラフ上の全ての辺 (実際に選ばれるかに拘らず) から最も重みの小さい辺を選ぶのに対して、プリム法は選択済みの部分グラフと接続している辺の中から最も重みの小さい辺を選ぶことから、計算量と記憶領域の点で若干優位な実装が可能である。
参考文献
- クラスカル法
 , プリム法
, プリム法 , シュタイナー木
, シュタイナー木
- 宮崎修一 "グラフ理論入門基本とアルゴリズム", 森北出版 (2015)