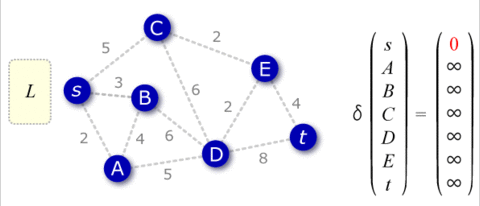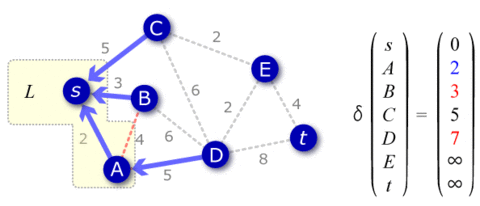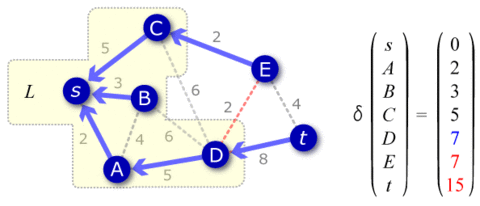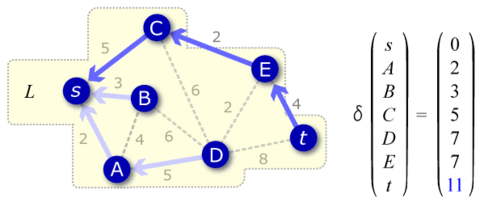
グラフ理論 序説
概要
グラフ理論 (graph theory) は数学的概念であるグラフを説明する理論。問題を頂点と辺からなるグラフに抽象化し、その離散構造そのものを論議の対象とする。
用語
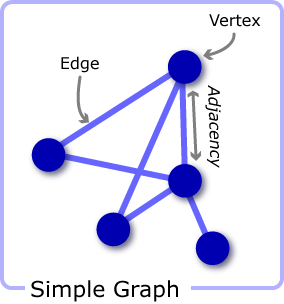
グラフ (graph)
いくつかの頂点と、2つの頂点をつなぐ辺の集合で構成される構造や抽象概念。グラフを構成する頂点集合 \(V\) と辺集合 \(E\) を合わせて \(G = (V, E)\) と表す。
頂点, 節点, ノード, サイト (vertex)
辺, リンク, 枝, ボンド (edge, link, branch)
グラフ上の 2 頂点を結ぶ線。頂点 \(u\) と \(v\) をつなぐ辺を \((u,v)\) と表す。グラフ上の辺の集合を \(E = \{(v_1, v_2), (v_1,v_3), \ldots\}\) と表す。
隣接 (adjacency)
接続 (connected)
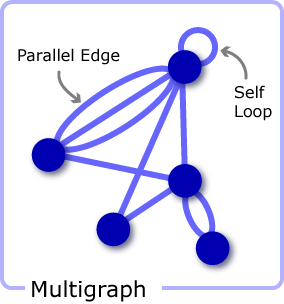
並列辺 (parallel edge)
自己ループ (self loop)
単純グラフ (simple graph)
多重グラフ (multigraph)
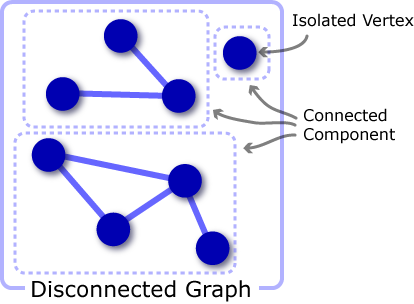
連結グラフ (connected graph)
非連結グラフ (disconnected graph)
孤立頂点 (isolated vertex)
連結成分 (connected component)
グラフ内で連結している単位。
重み付きグラフ (weighted graph)
それぞれの辺が重みの数値を持っているグラフ。単に重み付きグラフと表現した場合は辺重み付きグラフ (edge-weighted -) を指すことが多いが、頂点に重みが付けられている場合は頂点重み付けグラフ (vertex-weighted -) と言う。
有向グラフ (directed graph)
隣接行列 (adjacency matrix)
\(n\) 頂点の有限グラフに対して各頂点を行と列に配した \(n \times n\) 正方行列。頂点 \(v_i\) と \(v_j\) が隣接している場合、行列の \((i,j)\) 成分は 1、隣接していない場合 0 となる。重み付きグラフの場合は 1 の代わりに辺が持つ重みを成分とする。
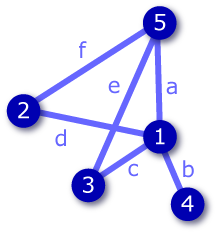\[\left( \begin{array}{cccccc} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 \end{array} \right) = \left(\begin{array}{cccccc} (1,1) & (1,2) & (1,3) & (1,4) & (1,5) \\ (2,1) & (2,2) & (2,3) & (2,4) & (2,5) \\ (3,1) & (3,2) & (3,3) & (3,4) & (3,5) \\ (4,1) & (4,2) & (4,3) & (4,4) & (4,5) \\ (5,1) & (5,2) & (5,3) & (5,4) & (5,5) \end{array} \right)\]接続行列 (incidence matrix)
\(n\) 頂点 \(m\) 辺の有限グラフに対して各頂点を行に、各辺を列に配した \(m \times n\) 行列。頂点 \(v_i\) と辺 \(e_j\) が接続している場合、行列の \((i, j)\) 成分は 1、接続していない場合 0 となる。従って列方向の総和は 2、行方向の総和は頂点 \(v_i\) の次数に等しい。
\[\left( \begin{array}{cccccc} 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 1 \end{array} \right) = \left(\begin{array}{cccccc} 1a & 1b & 1c & 1d & 1e & 1f \\ 2a & 2b & 2c & 2d & 2e & 2f \\ 3a & 3b & 3c & 3d & 3e & 3f \\ 4a & 4b & 4c & 4d & 4e & 4f \\ 5a & 5b & 5c & 5d & 5e & 5f \\ \end{array} \right)\]隣接リスト (adjacency list)
頂点とそれに隣接する頂点、または接続する辺をリストとして表現したもの。頂点数に対して辺の数が少ない隣接行列は疎行列となるため隣接リストで表現した方が記憶領域の効率が良い。
\[ \begin{array}{cl} 1 & : 2, 3, 4, 5 \\ 2 & : 1, 5 \\ 3 & : 1, 5 \\ 4 & : 1 \\ 5 & : 1, 2, 3 \end{array}\]
次数 (degree)
頂点に接続する辺の数。頂点 \(v\) の次数を \(d(v)\) と表す。またグラフ \(G\) 内で最も大きい次数をそのグラフの次数 \(\Delta(G)\) という。
歩道 (walk)
ある頂点から開始し接続している辺と頂点を交互にたどりながらグラフの任意の頂点たどり着く経路。同じ頂点や辺を複数回通過することができる。
小道 (trail)
道, 路 (path)
回路 (circuit)
起点と終点が同じ小道。
閉路 (cycle)
起点と終点が同じ道。
長さ (length)
距離 (distance)
\(u\), \(v\) を両端とする道の中で最も短いものの長さ。\(d(u,b)\) で表す。非連結グラフにおいて道が存在しない 2 頂点頂点の距離は無限大 \(\infty\) となる。
部分グラフ (subgaph)
グラフ \(G'=(V',E')\) のすべての頂点および辺がグラフ \(G=(V,E)\) と同一であるとき \(G'\) は \(G\) の部分グラフという。つまり \(V' \in V\) かつ \(E' \in E\) が成り立つ。
誘導部分グラフ (induced subgaph)
グラフ \(G\) の部分グラフ \(G'\) について、全ての頂点 \(V'\) が \(G\) と同じ辺を持つとき誘導部分グラフである。つまり \(E' = \{(u,v)|(u,v) \in E, u \in V', v \in V'\}\) が成り立つ。
補グラフ (complement graph)
グラフ \(G\) と同じ頂点 \(V\) を持ち、辺の有無が \(G\) と逆転しているグラフ。\(\bar{E} = \{(u,v)|u \in V, v \in V, (u,v) \not\in E\}\)
同型 (isomorphic)
頂点や辺の識別子を無視すれば本質的に同じ形をしているグラフ。\(G_1\) 上の任意の 2 頂点 \(u,v \in V_1\) とその辺 \((u,v)\) に対して、\(G_2\) 上の辺への変換 \((f(u), f(v)) \in E_2\) を満たす単射の \(f\) が存在する。このとき \(f\) を同型写像 (isomorphism) と呼ぶ。
木 (tree)
森 (forest)
葉 (leaf)
根 (root)
根付き木 (rooted tree)
平面的グラフ (planar graph)
2部グラフ (bipartite graph)
グラフ \(G\) の頂点集合 \(V\) を 2 つの部分集合に分けるとき、すべての辺の両端が 2 つの部分集合のそれぞれに属する頂点を結ぶ (つまり同じ部分集合内の頂点を結ぶことがない) ように分割できるグラフ。
完全2部グラフ (complete bipartite graph)
2部グラフで分けた頂点の部分集合 \(V_1\), \(V_2\) のすべての頂点に辺が存在するグラフ。\(|V_1|=n_1\), \(|V_2|=n_2\) のとき完全2部グラフ \(G\) を \(K_{n_1,n_2}\) と記す。
k-部グラフ (k-partite graph)
頂点集合 \(V\) について \(1 \leq i \leq k\), \(V_i\) の頂点同士をつなぐ辺が存在しない。頂点数 \(n\) のグラフは \(n\) 部グラフである。\(k\) 部グラフは \(k-1\) 部グラフでもある。
正則グラフ (regular graph)
k-正則グラフ (k-regular graph)
全ての頂点の次数が \(k\) である正則グラフ。頂点数 \(n\) の \(k\) 正則グラフにおいて次数の総和は \(nk\)、握手定理より辺の数は \(\frac{nk}{2}\) となる。
完全グラフ (complete graph, clique)
全ての頂点間に辺が存在するグラフ。頂点数 \(n\) の完全グラフを \(K_n\) と表す。\(K_n\) は \(k-1\) 正則グラフである。\(K_n\) の辺の数は \({}_nC_2 = \frac{n(n-1)}{2}\) である。
次数列
各頂点の次数を降順に並べた数列。ただしグラフには並列辺や自己ループは含まないものとする。ある数列がグラフの次数列となる場合、グラフ化可能列という。握手定理より次数列の総和は偶数となる。
オイラー回路 (Euler circuit)
グラフの各辺を必ず 1 度だけ通る回路a>。すべての頂点の次数が偶数であればグラフはオイラー回路を持つ。頂点を通過するとき、同じ辺を使って戻ることがないことから必ず頂点に接続した 2 本の辺、加えて始点から出発するときに 1 本と終点に到達するときに 1 本を使用する。従って辺の合計数は偶数でなければならず、またすべての頂点の次数は偶数でなければならない。
ハミルトン閉路 (Euler circuit)
モデル問題
最小シュタイナー木問題 (minimum Steiner tree problem)
グラフ上の頂点集合から任意の部分集合を作成し、その部分集合の頂点の全てを最小のコストでつなぐ問題。NP 困難であることが分かっている。最小シュタイナー問題参照。
定理
握手補題 (handshaking lemma)
全ての頂点の次数の総和は偶数となる。辺 \((u, v)\) の存在は頂点 \(u\) と \(v\) それぞれに +1 の次数を与え、グラフ全体として +2 の次数を与えているため。
隣接行列のべき乗
重みなし有向/無効グラフ \(G\) の隣接行列を \(A\) とするとき、その \(k\) 回の積 \(A^k\) の成分 \((i, j)\) は、\(G\) の頂点 \(v_i\) と \(v_j\) を両端とする道のうち長さが \(k\) となるものの数である。証明はP.11参照。
オイラーの公式
連結な平面グラフの頂点数を \(n\)、辺の数を \(m\)、辺によってできた閉面の数を \(k\) とすると \(n+k=m+2\) が成り立つ (\(k\) はグラフの外側も 1 と数える)。証明はP.16参照。
Havel-Hakimi の定理
非負整数の降順数列 \((a_1,a_2,\ldots,a_n)\) が単純グラフとしてグラフ可能列であるための必要十分条件は \((a_2-1,a_3-1,\ldots,a_{a_1+1}-1,a_{a_1+2},\ldots,a_n)\) を降順に並べた数列が単純グラフとしてグラフ化可能である。つまり 1)2番目～\(a_1+1\)番目までの数値を -1、2)先頭の \(a_1\) を消す、操作を行った数列がグラフ化可能であること。この操作を再帰的に繰り返すことで最後にすべての次数が 0 になればグラフ化可能列である。証明はP.21参照。
オイラー回路の定理
連結グラフ \(G\) がオイラー回路を持つための必要十分条件は \(G\) のすべての頂点の次数が偶数であること。証明はP.43参照。
ディラックの定理
\(G=(V,E)\), \(|V| \geq 3\) のとき、すべての頂点 \(v \in V\) に対して \(d(v) \geq \frac{|v|}{2}\) ならば \(G\) はハミルトン閉路を持つ。証明はP.46参照。
オーレの定理
\(G=(V,E)\), \(|V| \geq 3\) のとき、隣接していない任意の \(v\), \(w\) に対して \(d(v) + d(w) \geq |v|\) ならば \(G\) はハミルトン閉路を持つ。この定理はディラックの定理を真に含んでいる。証明はP.46参照。
参考文献
- 宮崎修一 "グラフ理論入門基本とアルゴリズム", 森北出版 (2015)
- 右田正夫, 今野紀雄 "マンガでわかる複雑ネットワーク巨大ネットワークがもつ法則を科学する", SBクリエイティブ (2011)