二項分布
0 = 黒、1 = 赤として赤の出る確率を \(p\)、範囲 \(0 \leq n \leq 6\) を調整できる二項分布のシミュレーション。+1 ボタンを押すと1回試行を行う。
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 確率 \(P(x)\) | |||||||
| \(NP(x)\) | |||||||
| 観測回数 \(N_\hat{x}\) |
 定義と性質
定義と性質
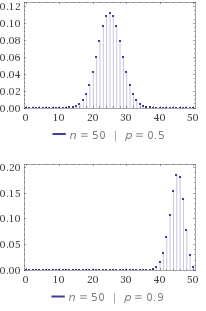
試行において 1 が観測される確率 \(p\) のベルヌーイ試行を \(n\) 回行ったとき (あるいは \(n\) 個同時に行ったとき) に 1 が \(x\) 個観測される確率は \(p\) と \(n\) をパラメータとした以下の確率質量関数で表される。\[ P(x; n,p) = \binom nx p^{x} (1-p)^{n-x} \] ここで二項係数は以下のように表される。\[ \binom nx = {}_n\mathrm{C}_x = \frac{n!}{x!(n-x)!} \] この分布 \(P(x)\) を二項分布 (binomial distribution) と呼ぶ。ベルヌーイ分布と似ているが、ベルヌーイ分布が 1 か 0 かの確率を表していたのに対して、二項分布は 1 がいくつ観測されたかの確率を表している点に注意。
 共通性と近似
共通性と近似
 ベルヌーイ分布との共通性
ベルヌーイ分布との共通性
ベルヌーイ試行の結果を \(b_i \in \{0, 1\}\) と表せば \(x\) は \(b\) の合計で表すことができる。\[ x = \sum_{i=1}^n b_i \] 特に \(n=1\) とした場合に二項分布はベルヌーイ分布と等しくなる。これは \(n=1\) で \(x\) は \(b_1\) と等しくなることから \(b\) の分布と同じ意味になることから分かる。
 ポアソン分布との近似
ポアソン分布との近似
ポアソン分布は \(f(x;\lambda) = \frac{\lambda^x e^{-\lambda}}{x!}\) で表される。\(np = \lambda\) として \(p \to 0, n \to \infty\) としたときに二項分布はポアソン分布となる。これはまれにしか起きない (\(p\sim 0\)) 事象を大量に観測した (\(n\sim \infty\)) ときの状況でポアソンの少数の法則と呼ばれる。
 アルゴリズム
アルゴリズム
 二項分布の試行関数
二項分布の試行関数
二項分布に従う整数 \(x \in (0, 1, \ldots, n)\) を返す関数について考える。この場合ベルヌーイ試行と同様に一様疑似乱数が \(p\) より小さいかを \(n\) 回判定し true であった数を返せば良い。
def trial(n:Int, p:Double):Int = (0 to n).count{ _ => math.random() < p }scala> trial(5, 0.6)
res0: Int = 3
scala> trial(5, 0.6)
res1: Int = 2
scala> trial(5, 0.6)
res2: Int = 4Scala の部分適用を使ってあらかじめパラメータ \(n, p\) が束縛された試行関数を生成できるようにしても良いだろう。
scala> def trial(n:Int, p:Double)():Int = (0 to n).count{ _ => math.random() < p }
trial: (n: Int, p: Double)()Int
scala> val x = trial(5, 0.6) _
x: () => Int = $$Lambda$1171/2060445311@47a1bf14
scala> x()
res0: Int = 5 二項係数
二項係数
階乗は小さな \(n\) に対してもオーバーフローを起こしやすいため、二項係数の演算では対数で求めた後に指数化すると良い。\[ \begin{align*} \binom nx & = {\rm exp}\left\{\log \frac{n!}{x!(n-x)!}\right\} \\ & = {\rm exp}\left\{\log n! - \log x! - \log (n-x)!\right\} \end{align*} \] ここでは対数階乗関数で実装した factorialln() を使用する。
def coefficient(n:Int, k:Int):Double = {
math.floor(0.5 + math.exp(factorialln(n) - factorialln(k) - factorialln(n-k)))
}本来の二項係数は整数となるが、この結果には浮動小数点演算の丸めによる若干の誤差が含まれる。この誤差を解消する目的で計算値に 0.5 を足して floor() を適用している (誤差が 0.25 に近くなるようであれば十分に大きな数であるため一の位の操作は無視できる)。
 確率関数
確率関数
二項分布の確率関数は指数と階乗を含むため数値演算上のオーバーフローを起こしやすいが、一度対数化してから指数演算を行うと簡単になる。\[ \begin{align*} P(x; n,p) & = {\rm exp}\left\{\log \binom nx + x \log p + (n-x) \log (1-p)\right\} \\ & = {\rm exp}\left\{\log n! - \log x! - \log (n-x)! + x \log p + (n-x) \log (1-p)\right\} \\ \end{align*} \]
上記より二項分布の確率関数は以下のように実装できる。分布のパラメータである \(n, p\) は Scala の部分適用によって束縛できるようにしている。
def p(n:Int, p:Double)(x:Int):Double = math.exp(
factorialln(n) - factorialln(x) - factorialln(n - x) +
x * math.log(p) + (n - x) * math.log(1 - p)
)実行結果は以下の通り。分かりやすいように部分適用は名前付きパラメータで呼び出している。
scala> val p6 = p(n=6, p=0.6)
p6: Int => Double = $$Lambda$1598/1837120736@e78bbcc
scala> for(x <- 0 to 6) println(p6(x))
0.004096000000000002
0.03686400000000005
0.13824000000000003
0.2764800000000003
0.31104
0.18662400000000007
0.04665599999999999
scala> (for(x <- 0 to 6) yield p6(x)).sum
res69: Double = 1.0000000000000004

