ディリクレ分布

Takami Torao
  • このエントリーをはてなブックマークに追加
\( \def\vector#1{\boldsymbol{#1}} \) \( \newcommand{\argmax}{\mathop{\rm argmax}\limits} \)

\(K=3\) 次元での任意の \(\vector{\alpha}\) に対して取りうる \(\vector{p}\) の確率分布をヒートマップで表すシミュレーション。\(\vector{p} = (p_1, p_2, 1-p_1-p_2)\) であることから \(p_3\) を省略し \(p_1\) と \(p_2\) の 2 次元で表現している。ヒートマップ上での白抜けは発散を示している。

\(\vector{\alpha} = (\) , , \()\)
期待値 \(\vector{E}(\vector{p}) = \) (?,?,?)
最頻値 \(\hat{\vector{\mu}} =　\) (?,?,?)
分散 \(\vector{\sigma}^2 (\vector{p}) = \) (?,?,?)

定義と性質

ディリクレ分布 (dirichlet distribution) は独立した事象 \(k \in \{1, 2, \cdots, K\}\) がそれぞれ \(x_k=\alpha_k - 1\) 回観測されたときに各事象の生起確率が \(p_k\) である確率を示す連続した確率密度関数。\[ \begin{equation} {\rm Dir}(\vector{p}; \vector{\alpha}) = \frac{\Gamma \left(\sum_{k=1}^K \alpha_k\right)}{\prod_{k=1}^K \Gamma(\alpha_k)} \prod_{k=1}^K p_k^{\alpha_k-1} \label{dirichlet_distribution} \end{equation} \] \(\vector{\alpha}\) がすべて整数であれば \(\Gamma(n)=(n-1)!\) と置き換えてもよい。\[ {\rm Dir}(\vector{p}; \vector{\alpha}) = \frac{\left\{(\sum_{k=1}^K \alpha_k) - 1\right\}!}{\prod_{k=1}^K (\alpha_k - 1)!} \prod_{k=1}^K p_k^{\alpha_k-1} \]

ここで \(0 < \alpha_k < 1\) の範囲において \(p_k=0\) となる部分で \(p_k^{\alpha_k-1}\) が発散することに注意。\[ p_k^{\alpha_k-1} = \left\{ \begin{array}{ll} 0 & (\alpha \geq 1) \\ \infty & (0 < \alpha_k < 1) \end{array} \right. \]

\(\sum_K x_k = n\)、\(\sum_K \alpha_k = A\) としたとき、ディリクレ分布における期待値 \(\vector{E}(\vector{p})\)、最頻値 \(\hat{\vector{\mu}}\)、分散 \(\vector{\sigma^2}(\vector{p})\) は以下のように表される。\[ \begin{align*} E(p_k) &= \frac{\alpha_k}{A} \\ \hat{\mu}_k &= \frac{\alpha_k-1}{A - K}, \ \ \alpha_k > 1 \\ \sigma^2(p_k) &= \frac{\alpha_k (A - \alpha_k)}{A^2 (A+1)} \end{align*} \] 多項分布の推定で導出した MAP 推定の最頻値 \(\hat{\mu}_{{\rm map},k}\) は \(\alpha'_k = \alpha_k + x_k\) としたディリクレ分布の最頻値と同じである。

事象のモデルは多項分布 \({\rm Multi}(\vector{x}|\vector{p},n)\) と同じであり、実際、多項分布の自然共役分布であることから、ベイズの定理で多項分布を尤度関数としたときの事前確率、事後確率として使われている。

多項分布が事象 \(k\) の生起確率 \(p_k\) から観測数 \(x_k\) となる確率分布を表しているのに対して、ディリクレ分布は実際の観測数 \(x_k=\alpha_k-1\) から生起確率 \(p_k\) がどこにあるかの確率分布を表している。

ディリクレ分布の可視化

\(\vector{\alpha}\) を変化させて得られるディレクリ分布からその意味を考えてみよう。

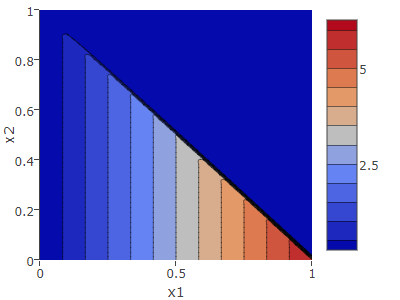
一様分布 \(\alpha_k=1\)

α=(1,1,1) \(\vector{\alpha} = (1, 1, 1)\) は全ての \(\vector{p}\) で一様な確率分布となる。事象 \(k\) の観測数が \(x_k=\alpha_k-1\) であることを考えれば \(\alpha_k=1\) はまだ一つも有効なデータを観測していないことを表している。推定に利用できるデータがまだ存在しない状況では全ての生起確率は均等な確かさという意味である。一様分布が事前確率に使用されるとき無情報事前確率と呼ばれる。

対称ディリクレ分布 \(\alpha_k=2\)

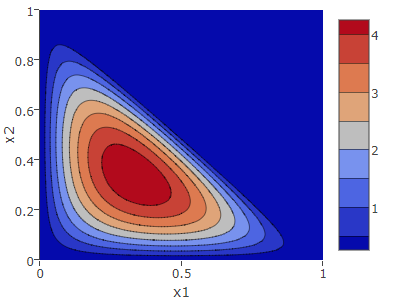α=(2,2,2) \(\vector{\alpha} = (2, 2, 2)\) のように \(\alpha_k\) がすべて等しい分布を対称ディリクレ分布と呼ぶ。期待値、最頻値ともに \(K\) 次元の中央となる \(\hat{\vector{\mu}} = (\frac{1}{K}, \ldots)\) に存在する。この意味は「すべての事象が同じ回数出現した観測結果から導かれる最も妥当な推定は全ての生起確率が等しいこと」である。

対称ディリクレ分布 \(\alpha_k=10\)

α=(10,10,10) \(\vector{\alpha} = (10, 10, 10)\) も同様に対称ディリクレ分布であるが、\(\alpha_k=2\) のときよりもよりピークが鋭い (分散が小さい)。これは「すべての事象の出現回数が全て9となるケースは、出現回数が全て1となるケースよりまれで、したがって \(\alpha_k=2\) の時より『全ての生起確率が等しい』推定の確度が高い」ことを意味する。

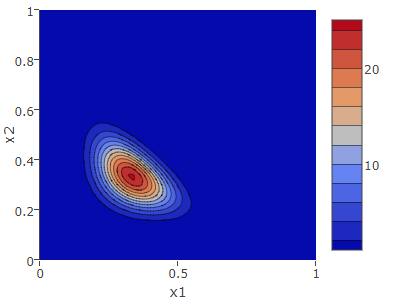
ディリクレ分布 \(\vector{\alpha} = (2, 1, 1)\)

α=(2,0,0) \(\vector{\alpha} = (2, 1, 1)\) とは \(k=1\) の事象が 1 回現れたという意味である。したがって、ディリクレ分布は \(\vector{p} = (1, 0, 0)\) が最も確度の高い生起確率であることを示している。\(\alpha_1\) を大きくするに従って \(\vector{p} = (1, 0, 0)\) の分布ピークも鋭くなってゆく (自分で確認せよ)。

ディリクレ分布 \(\vector{X} = (3, 2, 10)\)

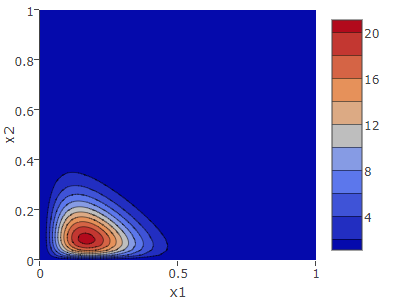α=(3,2,10) \(\vector{\alpha} = (3, 2, 10)\) からは \(k=3\) の事象が起きやすく、\(k=1\) と \(k=2\) を比較して「どちらかと言うと \(k=1\) の方が起きやすい」ことを示している。実際に分布のピークは \(p_3\) の高くなる \((0, 0)\) 付近に存在し \(p_2\) 方向よりも \(p_1\) 方向に少し寄っている。

対称ディリクレ分布 \(\alpha_k = 0.7\)

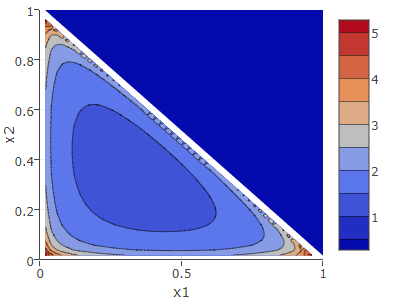α=(0.7,0.7,0.7) \(\vector{\alpha} = (0.7, 0.7, 0.7)\) について、\(0 < \alpha_k < 1\) をとるディリクレ分布は凸型ではなく凹型となり前述の通り \(p_k=0\) の部分で発散しているのが分かる。

このとき、\(p_k=0\) しか取り得ないという意味なのか \(p_k=0\) の値は取りえないという意味なのか、確率分布として発散の意味は何なのか (そもそも \(0 < \alpha_k < 1\) がどういう意味なのか想像が及んでいない)。\(p_k=0\) しかとりえないのであれば \(\alpha_k<0\) の対象ディリクレ分布は\(\vector{p}=(0, 0, 0)\) となり \(\sum p_k = 1\) を満たさなくなる。

実用例

多項分布を尤度関数としたときの事後確率となるため、カテゴリカル分布に従う試行を繰り返すときのそれぞれの事象 \(k\) の生起確率を求めるためによく使われている。特に自然言語処理ではトピックモデルで各トピックに単語が所属する生起確率を求める使い方がされている。

\({\rm Dir}(\vector{p}=\) \(; \vector{\alpha}=\) \()\)
\(K=\) 0
\(\vector{\alpha}=\) ()
\(\vector{x}=\) ()
\(\hat{\vector{\mu}}=\) ()
\(\vector{E}(\vector{p})=\) ()
\(\vector{\sigma}^2(\vector{p})=\) ()
\(\vector{p}=\) ()
\({\rm Dir}(\vector{p}; \vector{\alpha})=\) 0

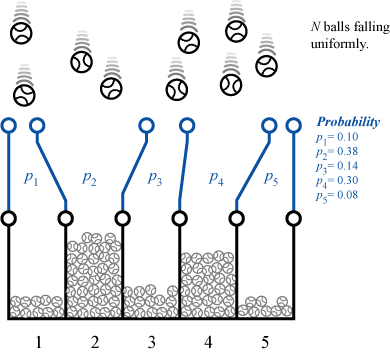
Example 1

一様に落ちてくる 10 個のボールが 5 つの区画にそれぞれ \(\vector{x} = (1, 4, 2, 2, 1)\) 入ったとき、各区画に入る確率 \(\vector{p}\) の期待値、最頻値、分散はそれぞれ以下のように表される。\[ \begin{align*} \vector{E}(\vector{p}) &= \frac{1}{15}(2, 5, 3, 3, 2) = (0.13, 0.33, 0.20, 0.20, 0.13) \\ \hat{\vector{\mu}} &= \frac{1}{10} (1, 4, 2, 2, 1) = (0.1, 0.4, 0.2, 0.2, 0.1) \\ \vector{\sigma}^2(\vector{p}) &= \frac{1}{3150}(26,50,36,36,26) = (0.008,0.016,0.011,0.011,0.008) \end{align*} \] 区画の広さの比率は (0.1, 0.4, 0.2, 0.2, 0.1) である可能性が最も高いが、確率のぶれを考慮して \(E\pm\sigma\) のように考えてもよい。

適当な点を採用して生起確率 \(\vector{p} = (0.10, 0.38, 0.14, 0.30, 0.08)\) に対応するディリクレ分布の値は: \[ \frac{\{(2+5+3+3+2)-1\}!}{1! \times 4! \times 2! \times 2! \times 1!} (0.10^1 \times 0.38^4 \times 0.14^2 \times 0.30^2 \times 0.08^1) = 267.21 \] となる。

多項分布 (Multinomial Distribution)

Example 2

\(K=5\) 種類のカードが出るガチャを考える。\(n=100\) 回引いて出た枚数がそれぞれ \(\vector{x} = (29, 31, 28, 10, 2)\) であったとき、それぞれの最頻値は以下のように表される。\[ \hat{\vector{\mu}} = \frac{1}{100} (29, 31, 28, 10, 2) = (0.29, 0.31, 0.28, 0.10, 0.02) \]

アルゴリズム

ディリクレ分布の式 (\(\ref{dirichlet_distribution}\)) は分数の形でガンマ関数が含まれているためオーバーフローを防ぐために対数を加減算してから指数化するとよいだろう。\[ {\rm Dir}(\vector{p}; \vector{\alpha}) = {\rm exp}\left\{ \log \Gamma\left(\sum_{k=1}^K \alpha_k\right) - \sum_{k=1}^K \log \Gamma(\alpha_k) + \sum_{k=1}^K (\alpha_k-1) \log p_k \right\} \]

ここでは対数ガンマ関数を使用している。

def dirichletln(alpha:Array[Double])(p:Array[Double]):Double = {
  assert(p.length == alpha.length && p.length != 0)
  val k = p.length;
  var Σa = 0.0
  var ΣlogΓa = 0.0
  var Σa1logp = 0.0
  for(k <- 0 until k){
    Σa += a(k)
    ΣlogΓa += gammaln(a(k))
    Σa1logp += (a(k) - 1) * math.log(p(k))
  }
  gammaln(Σa) - ΣlogΓa + Σa1logp
}

def dirichlet(alpha:Array[Double])(p:Array[Double]):Double = math.exp(dirichletln(p, a))

参照

  1. 多項分布の推定 (MOXBOX)