多項分布の推定

概要

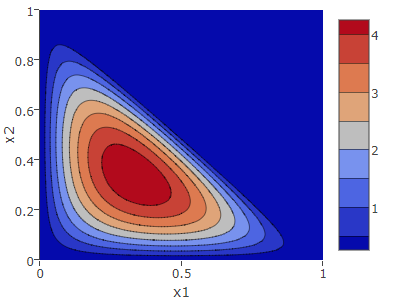
事象 \(k \in \{1,2,\cdots,K\}\) がそれぞれ生起確率 \(\vector{p} = (p_1,p_2,\cdots,p_K)\) に従って観測されるとき、標本 \(x=k\) が観測される確率 \(P(k)=p_k\) の分布はカテゴリカル分布に従う。さらにカテゴリカル分布に従う試行を \(n\) 回行ったとき、それぞれの事象の観測数を \(\vector{x} = (x_1, x_2, \cdots, x_K)\) とすると、ある標本 \(\vector{x}\) が観測される確率分布は多項分布 (\(\ref{multinomial_distribution}\)) に従う。\[ \begin{eqnarray} \label{multinomial_distribution} P(\vector{x}|\vector{p}) & = & \frac{n!}{\prod_{k=1}^K x_k!} \prod_{k=1}^K p_k^{x_k} \\ \sum_{k=1}^K p_k & = & 1, \ \ 0 \leq p_k \leq 1, \nonumber \\ \sum_{k=1}^K x_k & = & n, \ \ 0 \leq x_k \leq n \nonumber \end{eqnarray} \]

多項分布は \(K=2\) としたときに二項分布、\(n=1\) でカテゴリカル分布、\(K=2\), \(n=1\) でベルヌーイ分布とそれぞれ等しくなる。

多項分布の推定

多項分布に従う標本 \(\vector{x}\) が与えられたとき、最尤推定と MAP 推定から推測される生起確率 \(p_k\) はそれぞれ以下のように表される。\[ \begin{eqnarray} \hat{\mu}_{{\rm mle},k} & = & \frac{x_k}{n} \label{mu_mle}\\ \hat{\mu}_{{\rm map},k} & = & \frac{\alpha_k - 1 + x_k}{n - K + \sum_{j=1}^K \alpha_j}, \ \ \alpha_k \geq 1 \label{mu_map} \end{eqnarray} \] ここで \(\alpha_k\) は事前確率として使用するディリクレ分布のハイパーパラメータである。

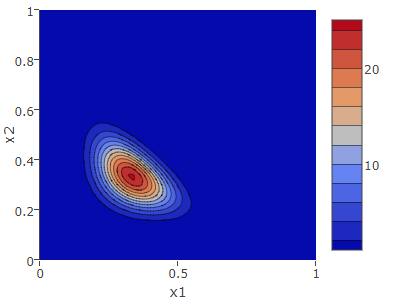
ベイズ推定による事後確率はディリクレ分布となり、期待値 \(E(p_k)\)、分散 \(\sigma^2_k\) と併せて以下のように表される。最頻値は \(\hat{\mu}_{{\rm map},k}\) と等しい。\[ \begin{eqnarray} P(\vector{p}|\vector{x}) & = & \frac{1}{B(\vector{\alpha} + \vector{x})} \prod_{k=1}^K p_k^{x_k + \alpha_k - 1} = {\rm Dir}(\vector{p}; \vector{\alpha} + \vector{x}) \label{bayes_prob} \\ B(\vector{\alpha}) & = & \frac{\prod_{k=1}^K \Gamma(\alpha_k)}{\Gamma(\sum_{k=1}^K \alpha_k)} \label{beta_function} \\ E(p_k) & = & \frac{\alpha_k + x_k}{n + \sum_{j=1}^K \alpha_j}, \ \ \sigma^2_k = \frac{\alpha_k (\sum_{j=1}^K \alpha_j - \alpha_k)}{(\sum \alpha_j)^2 (\sum \alpha_j + 1)} \nonumber \end{eqnarray} \] ここで \(\Gamma(x)\) はガンマ関数、\(B(\alpha)\) はベータ関数を多変量に拡張した関数である。\(k=2\) とすると二項分布\(\times\)ベータ分布の事後確率と同じ式になる。

多項分布の同時確率

多項分布に従う標本 \(\vector{x}\) が \(m\) 個得られたとき、その同時確率は \(\prod_{i=1}^m P(\vector{x}_i)\) で表される。ただし最尤推定、MAP 推定、ベイズ推定ともに \(m\) には標本の区切り以上に意味はなくカテゴリカル分布に従う試行が延べ何回行われ、事象 \(k\) が何回観測されたかに注目した多項分布と等しい。\[ n' = \sum_{i=1}^m n_i, \ \ x_k' = \sum_{i=1}^m x_{i,k} \] 次章では多項分布の同時確率として導いた (\(\ref{mu_mle}\))、(\(\ref{mu_map}\)) が単一の多項分布から導いた結果と等しいことを示している。

各推定の収束実験

多項分布の試行に対して各推定方法での収束を現すシミュレーション。+1 ボタンを押すと試行を 1 回行う。生起確率 \(p\) は重み \(w\) で調整可能。重み 0 で \(K\) を減らすことができる。

尤度関数 = 多項分布の同時確率

多項分布に基づく \(\vector{x}=(x_1,x_2,\cdots,x_K)\) を \(m\) 個の標本 \((\vector{x}_1, \vector{x}_2, \ldots, \vector{x}_m) = \vector{X}\) として観測した場合、同時確率は以下のように表される。試行ごとに \(n_i\) も変化していることに注意。\[ \begin{eqnarray} P(\vector{X}|\vector{n},\vector{p}) & = & \prod_{i=1}^m \frac{n_i!}{\prod_{k=1}^K x_{i,k}!} \prod_{k=1}^K p_k^{x_{i,k}} \label{likelihood_function} \end{eqnarray} \]

実際にデータ \((\vector{x}_1, \vector{x}_2, \ldots, \vector{x}_m) = \vector{X}\) を観測したとき \(P(x_1,\cdots,x_m|n,p)\) は \(\vector{x}\) に対する推定確率 \(\mu\) を表す尤度関数となる。

ここで対数尤度関数は以下のように表される。\[ \begin{equation} \label{log_likelihood} \log P(\vector{X}|n,\vector{p}) = \sum_{i=1}^m \left( \log n_i! - \sum_{k=1}^K \log x_{i,k}! + \sum_{k=1}^K x_{i,k} \log p_k \right) \end{equation} \]

最尤推定

最尤推定は (対数) 尤度関数が最大値を取る \(\hat{\mu}_{\rm mle}\) を求める。つまり、対数尤度関数 (\(\ref{log_likelihood}\)) が極値となる位置の \(p\) を意味することから、対数尤度関数の微分値が 0 となる位置を求める。

ただし単純に式 (\(\ref{log_likelihood}\)) を偏微分しただけでは有効な値を求めることが出来ない。\[ \frac{\partial}{\partial p_k} \log P(\vector{x}|\vector{n},\vector{p}) = \frac{\sum_{i=1}^m x_{i,k}}{p_k} = 0 \]

この場合、ラグランジュの未定乗数法 (Lagrange multiplier method) を使用すると解を導くことができる。多項分布式 (\(\ref{multinomial_distribution}\)) の前提条件から \(p_k\) が関与している \(\sum_{k=1}^K p_k - 1 = 0\) を未定乗数法の条件 \(g(x)=0\) として追加する。\[ \begin{eqnarray} L & = & \log P(\vector{x}|\vector{n},\vector{p}) + \lambda \left(\sum_{k=1}^K p_k - 1 \right) \nonumber \\ & = & \sum_{i=1}^m \left(\log n_i! - \sum_{k=1}^K \log x_{i,k}! + \sum_{k=1}^K x_{i,k} \log p_k \right) + \lambda \left(\sum_{k=1}^K p_k - 1 \right) \label{laglange} \end{eqnarray} \]

ラグランジュ関数 (\(\ref{laglange}\)) を \(p_k\) についての偏微分し極値を求める。\[ \frac{\partial}{\partial p_k} \left\{ \sum_{i=1}^m \left(\log n_i! - \sum_{k=1}^K \log x_{i,k}! + \sum_{k=1}^K x_{i,k} \log p_k \right) + \lambda \left(\sum_{k=1}^K p_k - 1 \right) \right\} \\ = \sum_{i=1}^m x_{i,k} \frac{1}{p_k} + \lambda = 0 \\ p_k = - \frac{1}{\lambda}\sum_{i=1}^m x_{i,k} \]

ここで多項分布の前提条件 \(\sum_K p_k=1\)、\(\sum_K x_{i,k} = n_i\) を当てはめるとラグランジュ係数 \(\lambda\) を求めることができる。\[ \sum_{k=1}^K p_k = - \frac{1}{\lambda}\sum_{i=1}^m\sum_{k=1}^K x_{i,k} = - \frac{1}{\lambda}\sum_{i=1}^m n_i = 1 \\ \lambda = - \sum_{i=1}^m n_i = - N \]

\(N = \sum_m n_i\) はすべての試行の合計回数を意味する。以上より最尤推定による \(\hat{\mu}_{{\rm mle},}\) は各事象の全観測回数 \(X_k=\sum_K x_{i,k}\) をすべての観測数で平均化した値となる。\[ \hat{\mu}_{{\rm mle},k} = \frac{X_k}{N} \] この式から同時確率として導入した \(m\) は単なる標本の区切りの意味しかないことが分かる。同時確率の解釈「それぞれ \(n_i\) 回の試行を \(m\) 回行う」を 1 回に「延べ」て \(m=1\)、\(n' = N = \sum n_i\)、\(x'_k = \sum_i x_{i,k}\) と置き換えると以下のように表される。\[ \hat{\mu}_{{\rm mle},k} = \frac{x'_k}{n'} \] 以降この式は (\(\ref{mu_mle}\)) で表す。

MAP推定

MAP 推定はベイズ定理における事後確率 \(P(\mu|\vector{x})\) を最大化する位置の \(\hat{\mu}_{\rm map}\) を求める。\[ P(p|\vector{x}) = \frac{P(\vector{x}|p) P(p)}{P(\vector{x})} \]

エビデンスの \(P(\vector{x})\) はすでに観測済みの \(\vector{x}\) に対する確率であり、事後確率が最大となる \(p\) の結果には関与しないため無視する。\[ \begin{equation} P(p|\vector{x}) \propto P(\vector{x}|p) P(p) = P(x_1|p) P(x_2|p) \cdots P(x_m|p) P(p) \label{bayes_theorem} \end{equation} \]

ここで尤度関数 \(P(\vector{x}|p)\) は (\(\ref{likelihood_function}\)) で表されている。事前確率 \(P(p)\) はディリクレ分布として考えてみよう。

事前確率 = ディリクレ分布

ディリクレ分布は多項分布の自然共役分布であることから多項分布の事前確率を表すのによく用いられている。\[ \begin{eqnarray} {\rm Dir}(\vector{x};\vector{\alpha}) & = & \frac{1}{B(\vector{\alpha})} \prod_{k=1}^K x_k^{\alpha_k-1} \label{prior} \\ \log {\rm Dir}(\vector{x};\vector{\alpha}) & = & - \log B(\vector{\alpha}) + \sum_{k=1}^K (\alpha_k-1) \log x_k \label{log_prior} \end{eqnarray} \] 多変量ベータ関数 (\(\ref{beta_function}\)) \(B(\vector{\alpha})\) は確率変数 \(\vector{x}\) には関与していないため後の偏微分で取り除くことができる。

対数尤度 (\(\ref{log_likelihood}\))、対数事前確率 (\(\ref{log_prior}\)) ともに \(p_k\) に対して \(a + \log p_k\) の形になっておりこのまま偏微分しても極値を導くことができない。従って最尤推定と同様にラグランジュの未定乗数法を使用する。\[ \begin{align*} L & = \log P(\vector{x}|\vector{p}) P(\vector{p}) + \lambda \left(\sum_{k=1}^K p_k - 1 \right) \\ & = \sum_{i=1}^m \left( \log n_i! - \sum_{k=1}^K \log x_{i,k}! + \sum_{k=1}^K x_{i,k} \log p_k \right) - \log B(\vector{\alpha}) + \sum_{k=1}^K (\alpha_k-1) \log p_k + \lambda \left(\sum_{k=1}^K p_k - 1 \right) \end{align*} \]

ラグランジュ関数 \(L\) を \(p_k\) で偏微分して 0 となる極値を求めると MAP 推定の観点で最も確率の高い位置の \(\hat{\mu}_{\rm map}\) が得られる。\[ \begin{align*} \frac{\partial L}{\partial p_k} & = \sum_{i=1}^m \sum_{k=1}^K \frac{x_{i,k}}{p_k} + \sum_{k=1}^K \frac{(\alpha_k-1)}{p_k} + \lambda = 0 \\ p_k & = - \frac{1}{\lambda} \left\{\sum_{i=1}^m x_{i,k} + (\alpha_k-1) \right\} \\ \end{align*} \]

ここで最尤推定と同様に未定である \(\lambda\) を求める。\[ \begin{align*} \sum_{k=1}^K p_k & = - \frac{1}{\lambda} \sum_{k=1}^K \left\{\sum_{i=1}^m x_{i,k} + (\alpha_k-1) \right\} = 1 \\ \lambda & = - \sum_{k=1}^K \left\{\sum_{i=1}^m x_{i,k} + (\alpha_k-1) \right\} = -N -\sum_{k=1}^K \alpha_k + K \\ \end{align*} \]

以上より \(\hat{\mu}_{{\rm map},k}\) は以下の式にまとめることができる。\[ \hat{\mu}_{{\rm map},k} = \frac{\alpha_k - 1 + X_k}{N + \sum_{j=1}^K \alpha_j - K} \] これは最尤推定と同様に \(m\) に意味はなく「延べ」の出現数で表すことと等価である。\[ \hat{\mu}_{{\rm map},k} = \frac{\alpha_k - 1 + x'_k}{n' + \sum_{j=1}^K \alpha_j - K} \] 以降この式は (\(\ref{mu_map}\)) で表す。

ベイズ推定

最尤推定、MAP 推定がもっとも確率の高くなる位置の \(p\) を導出していたのに対して (点推定) ベイズ推定は確率分布を導出する (区間推定)。

ベイズの定理 (\(\ref{bayes_theorem}\)) より、尤度関数とする多項分布 (\(\ref{multinomial_distribution}\)) と事前確率とするディリクレ分布 (\(\ref{prior}\)) を適用すると、事後確率 \(P(\vector{p}|\vector{x})\) はディリクレ分布 \({\rm Dir}(\vector{p}; \vector{\alpha}+\vector{x})\) に比例していることが分かる (言い換えると事後確率はディリクレ分布と同じ形をしている)。\[ \begin{align*} P(\vector{p}|\vector{x}) & \propto {\rm Multi}(\vector{x}|\vector{p},K) \, {\rm Dir}(\vector{p}; \vector{\alpha}) \\ & = \left\{ \frac{n!}{\prod_{k=1}^K x_k!} \prod_{k=1}^K p_k^{x_k} \right\} \left\{ \frac{\Gamma(\sum_{k=1}^K \alpha_k)}{\prod_{k=1}^K \Gamma(\alpha_k)} \prod_{k=1}^K p_k^{\alpha_k-1} \right\} \\ & \propto \prod_{k=1}^K p_k^{x_k} \prod_{k=1}^K p_k^{\alpha_k-1} = \prod_{k=1}^K p_k^{x_k + \alpha_k-1} \end{align*} \]

ディリクレ分布 \({\rm Dir}(\vector{p}; \vector{\alpha}+\vector{x})\) は積分して 1 となる確率密度関数であるため、上式に正規化項 \(\frac{1}{B(\vector{\alpha}+\vector{x})}\) を掛ければ事後確率とすることができる。\[ \begin{equation} \label{bayes_inferential} P(\vector{p}|\vector{x}) = \frac{1}{B(\vector{\alpha}+\vector{x})} \prod_{k=1}^K p_k^{x_k + \alpha_k-1} = {\rm Dir}(\vector{p}; \vector{\alpha}+\vector{x}) \end{equation} \] MAP 推定ではこのディリクレ分布の最頻値 (最も確率が高くなる位置の \(p\)) を求めていたことになる。

ディリクレ分布は \(\alpha\) が大きくなるにつれ分散が小さくなり鋭い分布となる。この結果から \(\alpha\) に観測回数の \(x\) が逐次加算されてゆくことが分かるため、観測回数 \(n\) が多くなれば事後確率の確度の高い範囲も特定されてゆくことが分かる。

尤度関数が多項分布の同時確率 \({\rm Multi}(\vector{x}_1,\vector{x}_2,\cdots,\vector{x}_m|\vector{p},K)\) となる場合でも各事象の観測回数が \(x_k \to \sum_{i=1}^m x_{i,k}\) となり、最尤推定、MAP 推定と同様に事象 \(k\) に対する「延べ」の観測回数の意味になる。

ハイパーパラメータ \(\alpha\)

ディリクレ分布と \(\alpha\)

ディリクレ分布はハイパーパラメータ \(\vector{\alpha}\) によって分布の形が決まる。\(\alpha\) が大きくなるに従い分散は小さくなり推定の範囲は絞られる。これは観測数 \(\vector{x}\) の加算によって事後確率がより確定的になることからも自然だろう。

\(\alpha=2\)

\(\alpha=10\)

ディリクレ分布での範囲は \(\alpha \gt 0\) で定義していたが、ベイズ推定の事後確率では \(0 \lt \alpha_k \lt 1\) の範囲で負の事後確率が現れるため \(\alpha_k \geq 1\) の範囲でなければならない。

すべての \(\alpha_k\) を 1 とした場合、ディリクレ分布は一様な無情報事前分布となり、事後確率は尤度関数 (多項分布) と同じ分布になる。このため事後確率の最頻値である MAP 推定は \(\hat{\mu}_{{\rm map},k} = \frac{x_k}{n}\) となり最尤推定の \(\hat{\mu}_{{\rm mle},k}\) と等しくなる。

またすべての \(\alpha\) を 2 とした場合 \(\hat{\mu}_{{\rm map},k} = \frac{1 + x_k}{n + K}\) はラプラススムージングと等しくなる。

ベイズ推定における \(\alpha\) の意味

事後確率において \({\rm Dir}(\vector{p};\vector{\alpha}+\vector{x})\) と表されることからも分かるように、ベイズ推定での \(\alpha_k\) は対応する事象の観測数 \(x_k\) の初期値を意味する。

つまり、各事象の観測数 \(x_k\) の比率に何らかの想定があるのであれば、それを反映した \(\alpha_k\) を設定することで観測数が少ない状況での過学習を抑えて精度を上げることができる。観測数 \(n\) が十分に大きくなれば \(\alpha_k\) の影響よりも観測から得られた \(x_k\) が確率を支配するようになるだろう。

例えば \(x_1\) が \(x_2\) の 2 倍程度出現することが分かっているのであれば \(\vector{\alpha} = (4, 2)\) とすることで \(n \simeq 10\) 程度は \(x_k\) の影響を抑えることができる。この比率がもっと確信的なら \(\vector{\alpha} = (10, 20)\) とすれば \(n \simeq 50\) 程度は影響が続くだろう。この挙動は実験のセクションで試してみると良い。

\(\alpha\) による調整は実用面で有用だが結果の恣意的な誘導も可能となる。全観測数 \(n\) に対して大きすぎる \(\alpha\) は観測や試行そのものが意味をなさなくなるだろう。

経験ベイズ法による \(\alpha\) の決定

経験ベイズ法 (empirical Bayes method) は既に観測されている \(\vector{x}\) の生起確率が最も高くなる \(\vector{\alpha}\) を求める方法。周辺化した周辺尤度 (marginal likelihood) \(P(\vector{x}; \vector{\alpha})\) を最大化する \(\vector{\alpha}\) を決定する。ある \(\vector{\alpha}\) に対する観測値 \(\vector{x}\) の生起確率は以下のように表される。\[ P(\vector{x}; \vector{\alpha}) = \int P(\vector{x}|\vector{p}) P(\vector{p}|\vector{\alpha}) d\vector{p} \] この対数を取って最大値となる \(\alpha\) を求めるところだが: \[ \argmax_\alpha P(\vector{x}|\vector{\alpha}) = \argmax_\alpha \log P(\vector{x}|\vector{\alpha}) \] 実際のところ周辺尤度を最大化する \(\alpha\) を解析的に求めることは難しく、数値演算で近似を行うのが一般的である。トピックモデルでは不動点反復法で収束させている。また情報認識「経験ベイズ法」ではラプラス近似を用いている。詳細はそれらのを参照して頂きたい。

実用例

文書中の単語の出現確率 (ユニモデル)

\(m\) 個の文書の中から {alice, bob, carol, dave, それ以外} の単語の出現確率を推定する。1 文書中に現れる単語の出現数は多項分布に従うと考えられる。取り得る事象は \(k \in \{1:{\rm alice}, 2:{\rm bob}, 3:{\rm carol}, 4:{\rm dave}, 5:{\it other}\}\) の \(K=5\) である。

まず最初の文書が \(\vector{x}_{1}=(1, 0, 2, 0, 32)\) だった場合、最尤推定と MAP 推定 (\(\alpha=2\)) では以下のようになる。\[ \begin{align*} \hat{\vector{\mu}}_{\rm mle} & = (\frac{1}{35}, \frac{0}{35}, \frac{2}{35}, \frac{0}{35}, \frac{32}{35}) = (0.029, 0.000, 0.058, 0.000, 0.914) \\ \hat{\vector{\mu}}_{\rm map} & = (\frac{2}{40}, \frac{1}{40}, \frac{3}{40}, \frac{1}{40}, \frac{33}{40}) = (0.050, 0.025, 0.075, 0.025, 0.825) \end{align*} \]

次の文書が \(\vector{x}_{2}=(2, 1, 1, 0, 51)\) だった場合 \(N=90\) より: \[ \begin{align*} \hat{\vector{\mu}}_{\rm mle} & = (\frac{3}{90}, \frac{1}{90}, \frac{3}{90}, \frac{0}{90}, \frac{83}{90}) = (0.033, 0.011, 0.033, 0.000, 0.922) \\ \hat{\vector{\mu}}_{\rm map} & = (\frac{4}{95}, \frac{2}{95}, \frac{4}{95}, \frac{1}{95}, \frac{84}{95}) = (0.042, 0.021, 0.042, 0.011, 0.884) \end{align*} \]

ある文書群に含まれるすべての単語に対して出現確立を算出た多項分布はトピック数 1 のトピックモデル (ユニモデル) に相当する。

参考文献

1. 岩田具治 (2015), "トピックモデル (機械学習プロフェッショナルシリーズ)", 講談社
2. 杉山将 (2009), "情報認識「経験ベイズ法」", PDF