ラグランジュの未定乗数法
 概要
概要
ラグランジュの未定乗数法 (method of Lagrange multiplier) は制約付き最適化問題で極値を求めるための手法である。ある 1 つ以上の条件 \(g(x)=0\) の下で関数 \(f(x)\) が最大値/最小値を取ることを式 (\(\ref{optimal_consumption}\)) のように表す。\[ \begin{equation} \begin{aligned} & \text{maximize (or minimize)} & & f(x) \\ & \text{subject to} & & g_1(x) = 0 \\ & & & g_2(x) = 0 \\ & & & \vdots \\ & & & g_m(x) = 0 \\ \end{aligned} \label{optimal_consumption} \end{equation} \] ここで maximize または minimize を目的関数、subject to を制約式、制約式を満たすすべての変数の組を実行可能解と呼ぶ。
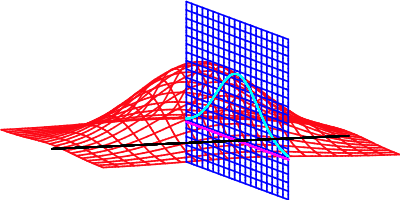
Fig 1 は式 (\(\ref{optimal_consumption}\)) を幾何学的に表している。赤で示した目的関数 \(f(x,y)\) において青で示した制約式 \(g(x,y)=0\) を満たす実行可能解は、それらの交差する水色の曲線である。ラグランジュの未定乗数法はこの曲線の極値となる \((x', y')\) を求める。
\(n\) 個の変数 \(\vector{x} = (x_1, x_2, \ldots, x_n)\) に対し \(m\) 個の条件 \[ g_1(\vector{x}) = g_2(\vector{x}) = \ldots = g_m(\vector{x}) = 0 \] のもとで関数 \(f(\vector{x})\) を最大化する \(\vector{x}\) について考える。
\(\vector{\lambda} = (\lambda_1, \ldots, \lambda_m)\) を導入して関数 \(L(\vector{x}, \vector{\lambda})\) を以下のように定義する。\[ L(\vector{x}, \vector{\lambda}) = f(\vector{x}) - \sum_{i=1}^m \lambda_i g_i(\vector{x}) \] ある極値 \(\vector{x}'\) が条件 \(\vector{g}(\vector{x}') = \vector{0}\) を満たすのであれば \[ \frac{\partial L}{\partial x_1'} = \cdots = \frac{\partial L}{\partial x_n'} = \frac{\partial L}{\partial \lambda_1'} = \cdots = \frac{\partial L}{\partial \lambda_m'} = 0 \] が成り立つ。ここで \(\vector{\lambda}\) をラグランジュ乗数、\(L(\vector{x}, \vector{\lambda})\) をラグランジュ関数と呼ぶ。実際の関数 \(f(\vector{x})\) をこの微分方程式に適用して解くことで極値となる \(\vector{x}'\) の値を得ることが出来る。
適用例
多項分布の推定において、対数関数 \( f(x) = a + b \log x \) の極値を求めるときに \(\frac{d P(x)}{d x} = \frac{b}{x} = 0\) となる問題をラグランジュの未定乗数法で回避している。