\(\chi^2\) 検定
概要
χ² 検定 (chi-square test) は χ² 分布を確率分布とする確率変数 \(\chi^2\) を求めることで行う検定。その利便性によって広く普及している。期待した分布と観測した分布が適合しているかを調べる適合度検定と、2 つの事象が関連しているかを調べる独立性検定がよく利用されている。
Table of Contents
\(\chi^2\) 適合度検定
χ² 適合度検定 (chi-square goodness-of-fit test) は、特定の離散確率分布に従う母集団を想定した期待値と、実際の観測から得られた頻度 (度数) と比較することで、それらが統計的に有意な差異を持つかを示す仮説検定。一般的には任意の確率分布から生成した \(k\) 個のカテゴリカル変数 (categorical variable) を持つカテゴリカル分布を離散確率分布として想定する。
以下のアプリは \(k\) 個のカテゴリカル変数に対するそれぞれの重み \(w_i\) と観測度数 \(x_i\) から χ² 検定により検定統計量 χ² と \(p\) 値を算出する。
| \(\alpha\) | 0.99 | 0.95 | 0.90 | 0.10 | 0.05 | 0.01 |
|---|---|---|---|---|---|---|
| \(\chi^2_\alpha\) |
χ² 適合度検定では離散確率分布の \(k\) 個のカテゴリカル変数それぞれでの期待値と観測頻度を統計的に比較する。そしてカテゴリカル変数のうち少なくとも 1 つで統計的な差異が認められるときに帰無仮説が棄却される。このとき、各カテゴリカル変数に少なくとも 5 (または 10) の観測頻度が必要と考えられている。理想的な母集団からのサンプリングであっても、観測データが 5 未満では近似が不十分となり帰無仮説が棄却される頻度は高くなる。
連続確率分布や \(k\) の極めて大きい離散確率分布では確率変数の粒度が高すぎることで十分な観測頻度を得ることが難しくなる。そこで確率変数を等幅の区間 (bin) に区切り、区間内の合計頻度または中央値をその区間の代表値として使用するビニング (binning) と呼ばれる前処理が行われる。例えば、ある分布に従う浮動小数点型の乱数を生成する関数を検定するために 0.001 区間ごとに観測頻度を設定するような処理である (従ってビニングは現実的に実施可能で目的の精度や有効数字を下回らない程度に解像度を落とす処理とも言える)。ビニングを行った区間はそのままカテゴリカル変数として使用できることから、一変量の連続確率分布に対してしばしば χ² 適合度検定が用いられる※1。
χ² 適合度検定の帰無仮説 \(H_0\) と対立仮説 \(H_a\) は以下のように定義される。
- \(H_0\): 観測頻度は仮定された分布に従う。
- \(H_a\): 観測頻度は仮定された分布に従わない。
χ² 適合度検定の統計量 χ² は期待値と観測値の差異の大きさを表す以外に意味はなく片側検定のみである。
- ※1連続確率分布に従う母集団からのサンプリングに対する検定は、アンダーソン-ダーリング検定
(Anderson-Darling test) やコルモゴロフ–スミルノフ検定 (Kolmogorov-Smirnov goodness-of-fit test) なども参照。
検定統計量と \(p\) 値
\(k\) 個のカテゴリカル変数のうち \(k-1\) 個が決まれば残りの 1 つは自動的に決定することから (\(k\) のうち 1 つは独立変数ではないことから) その標本の自由度 (degrees of freedom) は \(\phi=k-1\) である。あるカテゴリカル変数 \(i\) の生起確率を \(p_i\) としたとき、観測回数 \(n=\sum_i x_i\) に対しての観測頻度の期待値は \(\bar{x}_i=np_i\) となる。実際の観測頻度を \(x_i\) とすると検定統計量 χ² は確率変数 (\(\ref{chi2_variable}\)) で表される。\[ \begin{equation} \chi^2 = \sum_{i=1}^k \frac{(x_i - \bar{x}_i)^2}{\bar{x}_i} \label{chi2_variable} \end{equation} \]
\(r_i=\frac{x_i-\bar{x}_i}{\sqrt{\bar{x}_i}}\) をピアソン残差と呼ぶ。ここで式 (\(\ref{chi2_variable}\)) の \(x_i\) や \(\bar{x}_i\) は頻度 (度数) であり比率のような値ではない点に注意。χ² 分布表を使用する場合、有意水準 \(\alpha\) を決定し (一般的に 0.05 など)、分布表から自由度 \(\phi\) における棄却領域 \(\chi^2_\alpha\) を調べ、\(\chi^2 \gt \chi^2_\alpha\) であれば帰無仮説は棄却され対立仮説「観測値は想定の分布に従わない」を主張することができる。
自由度 \(\phi\) の χ² 分布の累積分布関数 \(F_\phi(x)\) に検定統計量 χ² を適用することで分布表を用いずに直接的に \(p\) 値を算出することができる。\[ \begin{equation} p = 1 - F_\phi(\chi^2) \label{p_value} \end{equation} \]
以下は自由度 \(\phi\) と検定統計量 χ² から \(p\) 値を計算する。
\(\chi^2\) 分布
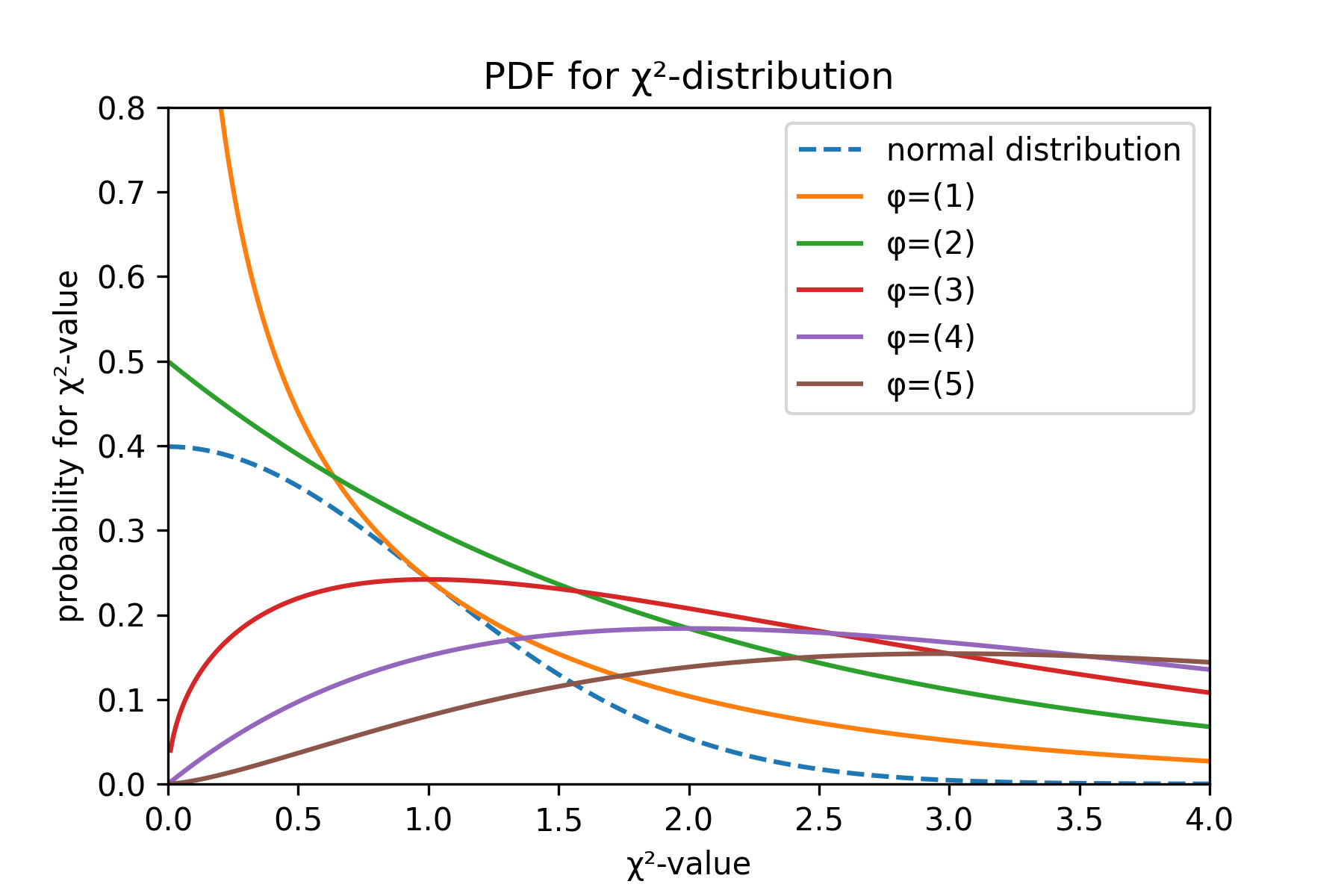
標準正規分布に従う \(\phi\) 個の独立な確率変数 \(Z_1,\ldots,Z_\phi\) の平方和 \(X=Z_1^2+\cdots+Z_\phi^2\) の分布を自由度 \(\phi\) の χ² 分布 (chi squared distribution; カイ二乗分布) と呼ぶ。χ² 分布の確率密度関数 \(f_\phi(x)\) は式 (\(\ref{chi2_dist}\)) で表される。\[ \begin{equation} f_\phi(x) = \frac{1}{2^{\frac{\phi}{2}} \ \Gamma\left(\frac{\phi}{2}\right)} x^{\frac{\phi}{2}-1} e^{-\frac{x}{2}} \label{chi2_dist} \end{equation} \] この χ² 分布は平均 \(\phi\)、分散 \(2\phi\) を持つ。Fig 1 は自由度 \(\phi\) に対する χ² 分布の確率密度関数の曲線の形を表している。
また累積分布関数 \(F_\phi(x)\) は式 (\(\ref{chi2_cum}\)) のように表される。\[ \begin{equation} F_\phi(x) = \frac{\gamma(\frac{\phi}{2}, \frac{x}{2})}{\Gamma(\frac{\phi}{2})} \label{chi2_cum} \end{equation} \] ここでガンマ関数と不完全ガンマ関数をそれぞれ \(\Gamma(a)=\int_0^\infty t^{a-1}e^{-t} dt\)、\(\gamma(a,x) = \int_0^x t^{a-1}e^{-t}dt\) とする。
scipy を使用した計算
確率密度関数 (PDF) や累積密度関数 (CDF) を人の手で計算することは現実的に困難であるため統計量 χ² に対する \(p\) 値や棄却域は統計ライブラリや χ² 分布表から得ることになる。例えば scipy.stats では以下に示す方法で統計量 χ² と \(p\) 値、各有意水準に対する棄却域などを算出することができる。
import numpy as np
from scipy.stats import chisquare, chi2
expected = np.array([16, 16, 16, 16, 16, 8])
observed = np.array([16, 18, 16, 14, 12, 12])
chi2_value, p_value = chisquare(observed, expected)
print("χ² = %f, p = %f" % (chi2_value, p_value))
for alpha in [0.10, 0.05, 0.01]:
print("Rejection Region[%.2f]: χ² > %.4f" % (alpha, chi2.ppf(1-alpha, len(expected) - 1)))χ² = 3.500000, p = 0.623388
Rejection Region[0.10]: χ² > 9.2364
Rejection Region[0.05]: χ² > 11.0705
Rejection Region[0.01]: χ² > 15.0863例: 日本における血液型の分布
Twitter で見かけたアンケート結果から日本人の血液型の分布この仮説は正しいだろうか?
ところで日本人の血液型の割合は、、O型32%、A型37%、B型22%、AB型9%らしいですよ、、実際本当なのか、、気になって夜も寝れません😔
- 深田えいみ大喜利お姉さん (@FUKADA0318) July 14, 2020
投票数の 346,561 から得る。
| 血液型 | 期待値 | 観測値 | ||
|---|---|---|---|---|
| O型 | A型 | B型 | AB型 |
\(\chi^2\) 独立性検定
χ² 検定がよく利用される状況は適合度検定の他に独立性の検定がある。χ² 独立性検定 (chi-square test of independence) は 2 つの事象 \(X\) と \(Y\) が有意な関連性を持つかを判断する。独立性とは \(X\) の結果が \(Y\) の結果に何の影響も与えないことを意味している。\(X\) の結果によって \(Y\) の結果が変化するとき事象 \(X\) と \(Y\) は独立ではなく関連している。
独立事象: 2 つの事象 \(X\) と \(Y\) に対して \(P(X \cap Y) = P(X) \cdot P(Y)\) が成り立つとき、\(X\) と \(Y\) は独立であるという。これは \(P(B|A) = P(B)\) または \(P(A|B) = P(A)\) が成り立つとき、と言い換えることもできる。
χ² 独立性検定は、2 つの事象が独立していることを帰無仮説とし、その帰無仮説を棄却することでそれらの事象が関連していることを示す。従って帰無仮説と対立仮説は以下のように設定する。
- 帰無仮説 \(H_0\): 事象 \(X\) と \(Y\) は独立している (関連がない)。
- 対立仮説 \(H_a\): 事象 \(X\) と \(Y\) は独立していない (関連がある)。
χ² 独立性検定は 2 つのカテゴリカル変数 \(X\) と \(Y\) をそれぞれ縦と横に配置した分割表に適用する検定である。変数 \(X\) における \(i\) 番目のカテゴリーと、変数 \(Y\) における \(j\) 番目のカテゴリーに属するデータの観測頻度を \(z_{i,j}\) とすると、期待度数 \(\bar{z}_{i,j}\) は独立性の帰無仮説の下で式 (\(\ref{expected_chi2_independence}\)) として表すことができる。\[ \begin{equation} \bar{z}_{i,j} = \frac{\displaystyle \sum_{k=1}^{n_x} z_{k,j} \times \sum_{k=1}^{n_y} z_{i,k}} {\displaystyle \sum_{k=1}^{n_x} \sum_{l=1}^{n_y} z_{k,l}} \label{expected_chi2_independence} \end{equation} \] もし変数 \(X\) と \(Y\) が独立であるという帰無仮説が正しいのであれば、式 (\(\ref{chi2_independence}\)) で表される統計量 χ² は近似的に自由度 \((n_x-1)(n_y-1)\) の χ² 分布に従う。\[ \begin{equation} \chi^2 = \sum_{i=1}^{n_x} \sum_{j=1}^{n_y} \frac{(z_{i,j} - \bar{z}_{i,j})^2}{\bar{z}_{i,j}} \label{chi2_independence} \end{equation} \]
式 (\(\ref{chi2_independence}\)) によって得られた統計量 \(\chi^2\) を使用して適合度検定と同様に \(p\) 値を算出し帰無仮説を評価することができる。
クラメールの関連係数
帰無仮説が棄却され変数 \(X\) と \(Y\) に関連があることが示されたとき、その関連の強さを示す指標として式 (\(\ref{cramers_v}\)) で表されるクラメールの関連係数 (Cramér's coefficient of association; クラメールの \(V\)) を使用することができる。\[ \begin{equation} V = \sqrt{\frac{\chi^2}{N \left\{ \min(n_x, n_y) - 1 \right\}}} \label{cramers_v} \end{equation} \] ここで \(N=\sum_{i=1}^{n_x} \sum_{j=1}^{n_y} z_{i,j}\) は総度数を表している。\(V\) は 0.0 (完全に独立) から 1.0 (完全に関連) の範囲の値を取る。この指標の明確な定義はないがこのサイトによれば 0.5 から 1.0 で強い関連を示していると考えて良いようである。