統計的仮説検定

2020年6月7日

概要

観測値の背景にある母集団の構造を仮定し、観測値の統計からその仮定が受け入れられるか、さもなくば拒否されるかを判断する統計的手法を統計的仮説検定 (statistical hypothesis testing) と呼ぶ。このとき仮定した構造のことを仮説 (hypothesis) と呼ぶ。

パラメトリック検定 (parametric test) は特定の分布に従っていることが想定される観測値に対して行う。実験やシミュレーション、または機械学習などから得られたデータの分布が想定したモデルと一致している (または一致していない) ことを主張するときの定量的な根拠として必要とされる。

一方、ノンパラメトリック検定 (non-parametric test) は前提となる分布を仮定せず、どのような分布に由来する観測値であっても適用可能である。これは各観測値の順位 (rank; 大小関係) を利用する。

概要
仮説
\(p\) 値と有意水準
様々な検定
1. 一標本 Z 検定
参考文献

仮説

統計的仮説検定はある信頼水準で帰無仮説 (null hypothesis) \(H_0\) を棄却 (reject) する方法を提供する。帰無仮説は母集団やデータ生成プロセスが特定の性質と等しい (有意な差がない) という主張 ─ つまり顕在する差異は観測やサンプリングによる偶然誤差として説明できる範囲のものであるという主張である。相違がゼロであることを示す仮定という意味で null という言葉が使われている。

帰無仮説とは反対に有意な違いがあることを主張する仮説を対立仮説 (alternative bypothesis) \(H_a\) と呼ぶ。仮説検定により帰無仮説が棄却された時に対立仮説が採用 (accept) される。\[ \begin{equation} \overset{帰無仮説 H_0}{X = Y} \ \Leftrightarrow \ \overset{対立仮説 H_a}{\left\{ \begin{array}{l} X \ne Y \\ X \lt Y \\ X \gt Y \end{array}\right.} \label{hypothesis} \end{equation} \] 関係式 (\(\ref{hypothesis}\)) において対立仮説に \(\ne\), \(\lt\), \(\gt\) のどれを設定するかで後述する \(p\) 値や信頼区間の算出方法が異なる点に注意。帰無仮説 \(\bar{x}=10\) に対する対立仮説として \(\bar{x} \lt 10\) や \(\bar{x} \gt 10\) を片側仮説、\(\bar{x} \neq 10\) を両側仮説といい、それぞれの検定を片側検定、両側検定という。慣例的に仮説検定によって何を明らかにするかを示すために問題設定とともに帰無仮説、対立仮説を宣言する。

(個人的に) 混乱しやすい 2 点を重ねて強調すると、1) 仮説検定において等しいことを主張する \(X=Y\) の仮定が帰無仮説である。2) 仮説検定は帰無仮説を棄却できるが帰無仮説が正しいと結論づけることのできる手段ではない (検定の非対称性)。

例えば公正なコイントスであれば表=+1, 裏=-1 のどちらも出る確率は等しいという帰無仮説 \(H_0\) があり、それに対して繰り返してコイントスを行って収集したデータから平均値を計算し、期待値がゼロと変わらないことを検定する。試行によって得られた平均値がゼロから離れている場合、帰無仮説は棄却され 1 回のコインフリップあたりの期待値がゼロではないという対立仮説 \(H_a\) を採用することができる。しかし、現実に母平均がゼロである場合にはどれだけ観測数を増やしても帰無仮説は棄却できず「等しくないとは言えない」と言うにとどまる。

\(p\) 値と有意水準

多くの検定では結果の解釈を統計的に定量化する検定統計量 (test statistic) を導入し、帰無仮説を棄却できるかを判断するために使用できる \(p\) 値 (\(p\)-value) と呼ばれる数量を算出する。\(p\) 値は「帰無仮説が真のときにこのような結果が観測される確率」を表している。したがって観測値に対する \(p\) 値が十分に小さければ帰無仮説 \(H_0\) は棄却され、データを観測した母集団が期待した分布を持っていないと結論づけることができる。

\(p\) 値に対して帰無仮説 \(H_0\) が棄却できるかどうかのしきい値を有意水準 (significance level) \(\alpha\) と表し経験的に 0.05 や 0.1, 0.03 などが採用される。結果的に \(p\)-value \(\lt \alpha\) であれば \(H_0\) は棄却することができる (つまり \(\alpha\) が大きくなると棄却の可能性が高くなる)。

例: 東京駅から秋葉原駅まで徒歩で 30 分かからないという仮説について考える。

帰無仮説 \(H_0\): 東京駅から秋葉原駅へは徒歩で 30 分 (以下) で到着する。

対立仮説 \(H_a\): 東京駅から秋葉原駅へは徒歩で 30 分よりの時間がかかる。

実際に \(n=100\) 人が東京駅から秋葉原駅まで歩いた平均の所要時間が \(\bar{x}=32\) 分だったとしよう。この観測結果から得られる \(p\) 値とは「\(H_0\) が真のときに \(\bar{x}\) が 32 分以上になる確率」つまり \(P(\bar{x} \ge 32{\rm min} \ | \ H_0={\rm true})\) を意味する。

ある検定手法に基づいて仮に \(p= 0.041\) が算出されたとすると、これが意味するところは「『東京駅-秋葉原駅間は徒歩30分かからない』が真であるなら 100 人が歩いて平均 \(\bar{x}\) が 32 分以上となるような観測値が得られる確率は 4.1% である」となる。これは一般に十分低いと見なされる確率であり、有意水準 \(\alpha=0.05\) とするならば \(H_0\) は棄却され「東京駅-秋葉原駅間は徒歩 30 分かからないとは考えにくい」と主張することができる。

後述の 3 つのシミュレーションはそれぞれの状況で \(p\) 値がどのように振る舞うかを窺うものである。\(p\) 値が一様に分布するケースは以下の 3 つがあることが見て取れる。

母集団が帰無仮説と一致するとき。
標本数が少ないとき。
母集団が想定する分布と一致していないとき。

すなはち、帰無仮説が真である (母集団と一致する) ことと、標本の質が不十分であることとは仮説検定の上では区別することができない。これは高い \(p\) 値が観測される状況とはまだ何かを判断できる状況ではないということを示しており、\(p\) 値が高いことは帰無仮説が正しいことを意味しない (帰無仮説を棄却できない) ことに通じている。エントロピーの観点から \(p\) 値が一様に分布するような帰無仮説を棄却できない状況には有用な情報量もなく、\(p\simeq 0\) のような帰無仮説が棄却される状況には情報量が多いという解釈もできる。

実験 1: 理想的な母集団に対する \(p\) 値

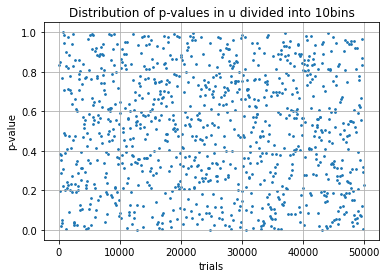
\(p\) 値は理想的な母集団に対して具体的にどのように振る舞うのだろうか。Fig 1 は「母集団は 0 以上 1 未満の一様乱数である」を帰無仮説とし、Mercenne Twister による一様乱数 \(u\) で生成した母集団からのサンプルを 0.1 幅の区間ごとに振り分けた観測頻度に対して、\(\chi^2\) 適合度検定で求めた \(p\) 値の分布を示している。つまり帰無仮説 \(H_0\) が真であると (ほぼ) みなして良い状況での \(p\) 値の振る舞いである。

母集団が帰無仮説と一致する理想的なケースでは、その標本数や試行回数にかかわらず \(p\) 値は 0 から 1 の間で一様に分布する。精度を上げるにつれて \(p=1\) に近づかないのは不自然に思えるかもしれないが、「\(p\) 値は理想的な母集団に対して偶然誤差のみの影響でその乖離が観測される確率である」の意味するところは「理想的な母集団に対する観測結果の \(p\) 値は常に一様分布となる」という性質と等価である。

Fig 1. 理想的な母集団に対する \(p\) 値の振る舞い。試行回数や観測頻度に拘らず 0 から 1 の間で一様に分布する。

%matplotlib inline
import matplotlib.pyplot as plt
import random
from scipy.stats import chisquare

bins = 10
trials = [t for t in range(bins * 10, 50000, bins * 5)]
p_value = []
random.seed(29056856)
for t in trials:
  observed = [0] * bins
  for _ in range(t):
    x = random.random()
    observed[int(x * bins)] += 1
  expected = [t / bins for i in range(bins)]
  chisq, p = chisquare(observed, expected)
  p_value.append(p)

plt.title("Distribution of p-values in u divided into 10bins")
plt.xlabel("trials")
plt.ylabel("p-value")
plt.grid(True)
plt.scatter(trials, p_value, s=3)

実験 2: 偏りを持つ母集団に対する \(p\) 値

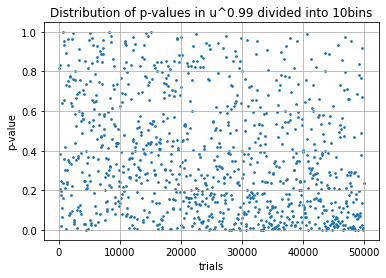
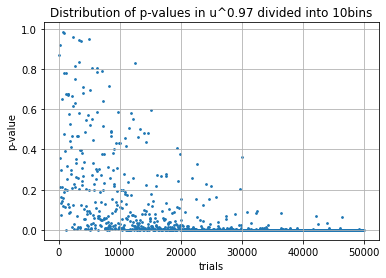
次に若干の偏りを追加した母集団に対する \(p\) 値の振る舞いを調べてみよう。Fig 2 は実験 1 における Mercenne Twister 乱数 \(u\) を \(u^b\) (\(b\in\{0.99,0.98,0.97\}\)) と置き換えたバージョンである。

母集団が偏りを持つケースでは、帰無仮説からの乖離が大きくなるにつれ、またその試行回数が増えるにつれて \(p\) 値の分布は 0 に偏ることがわかる。つまり、大局的には観測頻度や試行回数といった観測データを増やすことで \(p\) 値はより確定的な偏りを持ち棄却の精度を上げることができる。

Fig 2. 帰無仮説との差異を持つ母集団に対する \(p\) 値の振る舞い。乖離や試行回数の増加に伴い 0 に近づく。

%matplotlib inline
import matplotlib.pyplot as plt
import random
from scipy.stats import chisquare

bins = 10
bias = 0.99
trials = [t for t in range(bins * 10, 50000, bins * 5)]
p_value = []
random.seed(29056856)
for t in trials:
  observed = [0] * bins
  for _ in range(t):
    x = int(pow(random.random(), bias) * bins)
    observed[x] += 1
  expected = [t / bins for i in range(bins)]
  chisq, p = chisquare(observed, expected)
  p_value.append(p)

plt.title("Distribution of p-values in u^%.2f divided into 10bins" % bias)
plt.xlabel("trials")
plt.ylabel("p-value")
plt.grid(True)
plt.scatter(trials, p_value, s=3)

実験 3: 検定と適合しない母集団に対する \(p\) 値

〓

実験 3: Java 標準乱数の検定

Java 標準の疑似乱数生成器 Randomには、乱数シードを設定して最初に生成する double 型乱数が一様でないというよく知られた偏りが存在している。\(\chi^2\) 適合度検定を使用してこの偏りが統計的に有意なものかを検定してみよう。

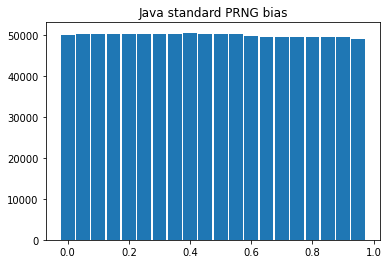
Fig 3. Java 標準の擬似乱数生成器の偏りが出る使い方でのヒストグラム。

Fig 3 は偏りが発生すると言われる方法で取得した乱数を 20 区画に分割して作成したヒストグラムである。この図からは偏りが明らかであるというほどの確信を持てないが、帰無仮説を「母集団は一様乱数である (≒ 全ての頻度は等しい)」とした \(\chi^2\) 適合度検定からは \(p=0.000046\) と算出された。有意水準 \(\alpha=0.05\) としたとき、\(p\) 値は \(\alpha\) に比べて低い値であるため、帰無仮説は棄却され、対立仮説「母集団は一様乱数ではない」を採用するのが妥当である。

なお Java 標準の乱数生成器において int 型乱数や 2 回目以降に生成される nextRandom() の値は一様な乱数となることが確認されている。

val random = new java.util.Random()
for(i <- 0 to 1000000) {
  random.setSeed(i)
  printf("%s\n", random.nextDouble())
}

%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import chisquare

df = pd.read_csv("java-prng.csv", names=["prng"])
bins = 20
observed = [0] * bins
for x in df["prng"]:
  observed[int(x * bins)] += 1

expected = [len(df["prng"]) / bins] * bins
chisq, p = chisquare(observed, expected)
print("p = %f" % p)

x = [i / bins for i in range(0, bins)]
plt.title("Java standard PRNG bias")
plt.bar(x, observed, width=1/bins*0.9)

様々な検定

t 検定

ある標本の平均値 \(\bar{x}\) は \(\mu\) と等しいか、\(\mu\) より大きいか、\(\mu\) より小さいか。

実験的に得られた観測値の平均 \(\bar{x}\) は期待値 (理論値) \(\mu\) と等しいか。

t 検定: 正規分布に従うと予想される 2 つの標本の母集団が同じかを判断する。

\(F\) 検定

F 検定 (F test) は 2 つの標本の分散 (標準偏差) が異なっているかを測定する統計的仮説検定。代表的な利用例は t 検定の予備検定である。

2020年7月7日(Tue) #ftest

\(t\) 検定

\(t\) 検定 (t-test; スチューデントの t) は正規分布に従う母集団から無作為に抽出した 2 つの標本が互いに異なるかを計測する仮説検定である。母集団の標準偏差が不明な場合は Z 検定の代わりに t 検定を使用する

2020年7月1日(Wed) #ttest

\(\chi^2\) 検定

χ² 検定 (chi-square test) は χ² 分布を確率分布とする確率変数 \(\chi^2\) を求めることで行う検定。その利便性によって広く普及している。期待した分布と観測した分布が適合しているかを調べる適合度検定と、2 つの事象が関連しているかを調べる独立性検定がよく利用されている。…

2020年7月10日(Fri) #chisquare

一標本 Z 検定

Z 検定 (z-test) は標本がある正規分布に従う母集団に由来するかを測定するために用いられる仮説検定。一標本 t 検定

t 検定と異なる点は 1) 母集団の標準偏差が既知であること (標本数が十分であれば標本の標準偏差で代用するケースもある) と、2) 多くの標本数が必要 (一般に 30 以上) なことである。Z 検定で使用する Z 分布は自由度が大きくなるにつれて t 分布と近似し、標本数が無限大になると完全に一致する。t 検定は標本数が多くなるにつれ分布計算が難しくなることからコンピュータが普及する前では Z 検定で代用されてきたが、近年では表計算や統計ライブラリによって t 分布の検定統計量を容易に計算できるようになったことから利用局面は減っている。

検定統計量 \(Z\) は式 (\(\ref{z_var}\)) で求めることができる。\[ \begin{equation} Z = \frac{\bar{x} - \mu}{\sigma / \sqrt{n}} \label{z_var} \end{equation} \] ここで \(\bar{x}\) は標本平均、\(\mu\) は母集団の平均、\(\sigma\) は母集団の標準偏差、\(n\) は標本数とする。得られた検定統計量 \(Z\) から Z 分布表を参照し \(p_0\) 値を特定する。この \(p_0\) は分布曲線左側の裾野の計測値であるため、どの対立仮説を採用するかによって \(p\) 値の計算方法が変わる。

帰無仮説 \(H_0\): 標本平均 \(\bar{x}\) は母集団の平均 \(\mu\) と等しい。
対立仮説 \(H_a\):
- 標本平均 \(\bar{x}\) は母集団の平均 \(\mu\) より大きい: \(p = 1 - p_0\)
- 標本平均 \(\bar{x}\) は母集団の平均 \(\mu\) より小さい: \(p = p_0\)
- 標本平均 \(\bar{x}\) は母集団の平均 \(\mu\) と等しくない: \(p = 2\times \min(p_0, 1-p_0)\)

\(p\) 値が有意水準 \(\alpha\) より小さい場合は帰無仮説を棄却して、標本と想定した母集団とに統計的な差異があることを示すことができる。そうでなければ、帰無仮説を棄却できず、標本が母集団と異なるとは言えない。