$ \def\vector#1{\boldsymbol{#1}} $

$F$ 検定

2020年7月7日 #ftest

概要

F 検定 (F test) は 2 つの標本の分散 (標準偏差) が異なっているかを測定する統計的仮説検定。代表的な利用例は t 検定の予備検定である。

以下は正規分布に従う 2 つの標本 $\vector{x}$ と $\vector{y}$ を入力すると両側及び片側検定の帰無仮説 $H_0$ が棄却されるかを見ることができる。

F-test calculator

$\vector{x}=$

$\vector{y}=$

$F=s_x^2/s_y^2=$

$\alpha$	$0.01$	$0.05$	$0.10$	$0.20$	$p$
$H_a:\sigma_x^2 \ne \sigma_y^2 \Leftrightarrow H_0$
$H_a:\sigma_x^2 \lt \sigma_y^2 \Leftrightarrow H_0$
$H_a:\sigma_x^2 \gt \sigma_y^2 \Leftrightarrow H_0$

表にマウスを乗せるとグラフの棄却域と日本語での結果の表現が変化する。

概要
統計量と確率分布
1. 検定統計量 F
2. F 分布
F 検定
1. 例1: 温度計の分散比較
参考文献

統計量と確率分布

F 検定は、正規分布に従う 2 つの母集団 $X$, $Y$ からランダムに抽出した標本 $\vector{x}$, $\vector{y}$ に対して、母分散の推定値である不偏分散 $s_x^2$, $s_y^2$ を算出し、その差異の検定統計量 $F$ と F 分布を用いてその差異が現実に発生しうる確率を算出し、有意水準 $\alpha$ と比較してそれぞれの母集団の真の母分散が等しいかを検定する。

検定統計量 F

2 つの母集団の分散が異なることを検定するためには、母集団から得られた 2 つの標本の分散の差異を変数 (統計量) とする確率分布を見つける必要がある。この統計量を求めるためにまず正規分布に従う変数の二乗和が $\chi^2$ 分布 (カイ二乗分布; chi-square) に従うことを思い出そう。

標準正規分布 $\mathcal{N}(0,1)$ に従う $\phi$ 個の独立な変数を $x_1,\ldots,x_\phi$ とするとき、これらの二乗和 $\sum_i x_i^2$ は自由度 $\phi$ の $\chi^2$ 分布に従う。\[ \sum_{i=1}^{\phi} x_i^2 \sim \chi^2_\phi \ \ \ \ \mbox{ここで $x \sim \mathcal{N}(0, 1)$} \]

確率変数 $x_1,\ldots,x_\phi$ が母平均 $\mu$、母分散 $\sigma^2$ の正規分布 $\mathcal{N}(\mu,\sigma^2)$ に従うのであれば、変数を $(x_i-\mu)/\sigma$ とすることで標準正規分布に従う変数に正規化することができる。従って、正規化した変数の二乗和 $\frac{1}{\sigma^2} \sum_i (x_i - \mu)^2$ も同じく自由度 $\phi$ の $\chi^2$ 分布に従う。\[ \frac{1}{\sigma^2} \sum_{i=1}^{\phi} (x_i - \mu)^2 \sim \chi^2_\phi \ \ \ \ \mbox{ここで $x \sim \mathcal{N}(\mu,\sigma^2)$} \]

一般的に母集団の真の平均 $\mu$ は知るすべがないため $\mu$ の代わりに標本平均 $\bar{x}$ を用いる。この場合、変数のうちの 1 つが独立ではなくなるため、自由度は標本数 $n$ を 1 つ減算した $\phi=n-1$ として表される。結果的に「正規分布 $\mathcal{N}(\mu,\sigma^2)$ に従う母集団から抽出した標本 $x$ に対して式 ($\ref{sum_square_follows_chi2}$) で示す変数は自由度 $n-1$ の $\chi^2$ 分布に従う」と考えることができる。\[ \begin{equation} \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \bar{x})^2 \sim \chi^2_{\phi=n-1} \label{sum_square_follows_chi2} \end{equation} \]

さて、F 検定で対象とする数量は母集団の分散である。母平均 $\mu$ と同様に母分散 $\sigma^2$ も知るすべがないことから、標本から推測される母分散 $\sigma^2$ の推定値である不偏分散 $s^2$ (unbiased variance) を使用する。\[ \begin{equation} s^2 = \frac{1}{\phi} \sum_{i=1}^{n} (x_i - \bar{x})^2 \label{sample_variance} \end{equation} \] この分母は標本 $x$ の自由度 $\phi=n-1$ で表すこともできる。

ここで式 ($\ref{sum_square_follows_chi2}$) に $1/\phi$ を乗算すると不偏分散 $s^2$ を用いた式 ($\ref{div_unbiased_by_var}$) に書き換えることができる。この操作は変数に対する定数の乗算であるため $\chi^2$ 分布に従う性質は維持される。\[ \begin{equation} \frac{1}{\phi} \cdot \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \bar{x})^2 = \frac{1}{\sigma^2} \left\{ \frac{1}{\phi} \sum_{i=1}^n (x_i - \bar{x})^2 \right\} = \frac{s^2}{\sigma^2} \sim \chi^2_{\phi=n-1} \label{div_unbiased_by_var} \end{equation} \]

さて、分散を用いた変数が従う確率分布は式 ($\ref{div_unbiased_by_var}$) で得られたが、この検定で興味があるのは 2 つの母集団の分散の差異である。ここで式 ($\ref{div_unbiased_by_var}$) を利用できるように、$\chi^2$ 分布に従う 2 つの変数の比 (つまり差異を表している) を変数とする確率分布を F 分布 (Snedecor's F-distribution) を導入する。

自由度 $\phi_1$ の $\chi^2$ 分布に従う変数を $z_1$、自由度 $\phi_2$ の $\chi^2$ 分布に従う変数を $z_2$ とすると、変数 $\frac{z_1/\phi_1}{z_2/\phi_2}$ は自由度 $(\phi_1,\phi_2)$ の F 分布に従う。

$\chi^2$ 分布に従う式 ($\ref{sum_square_follows_chi2}$) を $z$ と置き換えることで、式 ($\ref{seed_stat_value}$) で表されるような自由度 $\phi=(n_x-1,n_y-1)$ の F 分布に従う変数を得ることができる。\[ \begin{equation} \frac{z_1/\phi_1}{z_2/\phi_2} = \frac{ \left \{\sum_{i=1}^{n_x} (x_i-\bar{x})^2 / \sigma_x^2 \right\} / \phi_x }{ \left \{\sum_{i=1}^{n_y} (y_i-\bar{y})^2 / \sigma_y^2 \right\} / \phi_y } = \frac{s_x^2/\sigma_x^2}{s_y^2/\sigma_y^2} \sim F_{\phi=(n_x-1,n_y-1)} \label{seed_stat_value} \end{equation} \]

F 検定においては帰無仮説を $H_0: \sigma_x^2 = \sigma_y^2$ と設定することから統計量 $F$ を式 ($\ref{f_value}$) のように表すことができる。この $F$ 値は (見ての通りだが) 2 つの母集団の分散の比を表していることから、F 分布に適用すると「2 つの標本から得られた不偏分散の差異がある数量 $F$ となる確率」が得られることが分かる。\[ \begin{equation} F = s_x^2 / s_y^2 \label{f_value} \end{equation} \] $F$ 値は分散の比であるため必ず 0 以上の値をとる。

F 分布

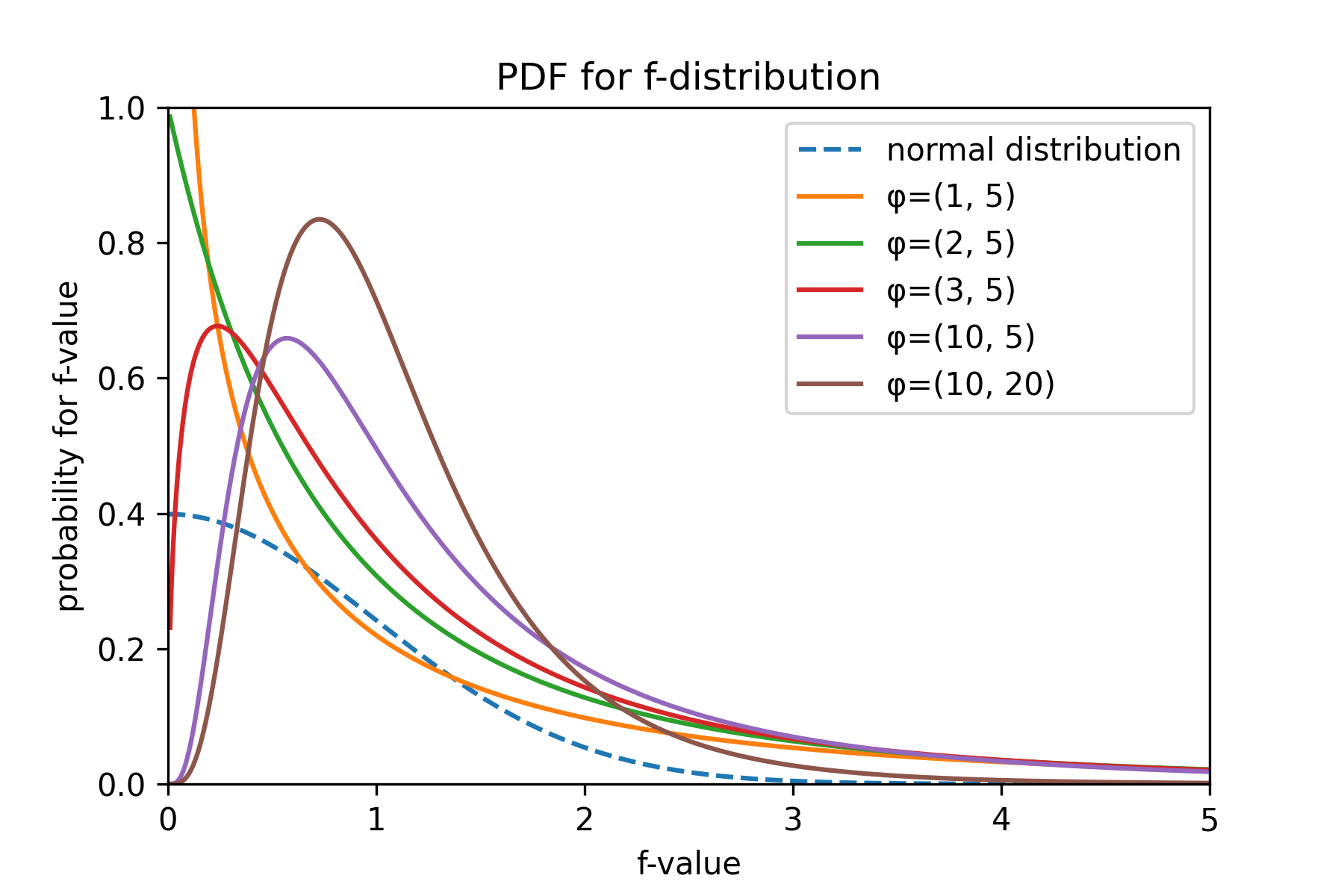
F 分布は式 ($\ref{f_value}$) の分子と分布の 2 つの自由度 $\phi=(\phi_x,\phi_y)$ の組み合わせによって Fig 1 に示すように形が決まる。

F 分布の確率密度関数 (PDF) は式 ($\ref{f_dist}$) で表されるように複雑であるため人手で解くことは現実的ではなく、通常は統計ライブラリの数値演算か F 分布表を使用する。ここで $\Gamma(x)$ はガンマ関数である。\[ \begin{equation} f_{\phi}(x) = \frac{ \Gamma \left( \frac{\phi_1 + \phi_2}{2} \right) x^{\frac{\phi_1-2}{2}} }{ \Gamma \left( \frac{\phi_1}{2} \right) \Gamma \left( \frac{\phi_2}{2} \right) \left( 1 + \frac{\phi_1}{\phi_2} x \right)^{\frac{\phi_1+\phi_2}{2}} } \left( \frac{\phi_1}{\phi_2} \right)^{\frac{\phi_1}{2}} \label{f_dist} \end{equation} \]

以下は scipy の統計ライブラリを使用して F 分布の統計量を算出するサンプルである。dfn (degree of freedom numerator)、dfd (degree of freedom denominator) はそれぞれ式 ($\ref{f_value}$) における分子の自由度 $\phi_x$ と分母の自由度 $\phi_y$ に対応している。

import scipy

dfn = 3   # degree of freedom numerator
dfd = 5   # degree of freedom denominator

mean, var, skew, kurt = scipy.stats.f.stats(dfn, dfd, moments="mvsk")
print("mean: %f, variance: %f, skewness: %f, kurtosis: %f" % (mean, var, skew, kurt))

# PDF (probability density function) and CDF (cumulative density function) for F=0.5
print("PDF(0.5, %d, %d) = %f" % (dfn, dfd, scipy.stats.f.pdf(0.5, dfn, dfd)))
print("CDF(0.5, %d, %d) = %f" % (dfn, dfd, scipy.stats.f.cdf(0.5, dfn, dfd)))

# 95% confidence intervals using PPF (percent point function)
f = scipy.stats.f.ppf(0.95, dfn, dfd)
print("PPF(0.95, %d, %d) = %f" % (dfn, dfd, f))
print("CDF(%f, %d, %d) = %f" % (f, dfn, dfd, scipy.stats.f.cdf(f, dfn, dfd)))

mean: 1.666667, variance: 11.111111, skewness: nan, kurtosis: nan
PDF(0.5, 3, 5) = 0.586015
CDF(0.5, 3, 5) = 0.301547
PPF(0.95, 3, 5) = 5.409451
CDF(5.409451, 3, 5) = 0.950000

$t$ を自由度 $\phi$ の t 分布に従う統計量とすると $t^2$ は自由度 $(1,\phi)$ の F 分布に従う。

F 検定

F 検定は、正規分布に従う 2 つの母集団 $X$, $Y$ の母分散 $\sigma_x^2$, $\sigma_y^2$ が等しいことを帰無仮説とし、それらが異なっているか (両側検定) またはどちらかが大きいか (片側検定) を検定する。

F 検定はしばしば二標本 t 検定において母集団の分散が一致していると想定できるか (等分散性) を判断するための予備検定に利用される。そのような予備検定で使用する場合は (論議の余地[1]はあるようだが) 慣例的に有意水準を $\alpha=0.20$ 程度に設定する。

自由度 $\phi$ の F 分布の累積密度関数 (CDF) $\int_0^x f_\phi(x) dx=p$ の逆関数を $\mathcal{F}_\phi^{-1}(p)=x$ とすると、F 検定の帰無仮説と対立仮説、および有意水準 $\alpha$ に対する棄却域は Table 1 のように表すことができる。数値演算に scipy を使用するのであれば $\mathcal{F}_\phi^{-1}(p)$ は scipy.stats.f.ppf(p, dfn, dfd) で求めることができる。

Table 1. 帰無仮説/対立仮説とそれぞれの棄却域。
帰無仮説	対立仮説	棄却域
$H_0:\sigma_x^2 = \sigma_y^2$	$H_a:\sigma_x^2 \ne \sigma_y^2$	$F \lt \mathcal{F}_\phi^{-1}(\alpha/2)$ または $F \gt \mathcal{F}_\phi^{-1}(1-\alpha/2)$
	$H_a:\sigma_x^2 \lt \sigma_y^2$	$F \lt \mathcal{F}_\phi^{-1}(\alpha)$
	$H_a:\sigma_x^2 \gt \sigma_y^2$	$F \gt \mathcal{F}_\phi^{-1}(1-\alpha)$

$F$ が 1 以上となる記載しかない F 分布表を使用する場合は、不偏分散の大きい方を分子となる ($x$) とすることで $F$ を 1 以上にすることができる。数値演算で求める場合はその限りではない。

例1: 温度計の分散比較

問. 工場施設内に設置している温度計を新しくすることになった。新しく導入する 16 個の温度計を $X$、既に設置している旧式の 14 個の温度計を $Y$ とする。$X$ と $Y$ を一箇所に集めて同じ条件で温度を計測しそれぞれの不偏分散を求めたところ $s_x^2=1.187$, $s_y^2=4.243$ という結果が得られた。新しい温度計は以前の温度計と比べて数値の散らばりが小さいと言って良いだろうか?

答. 式 ($\ref{f_value}$) より F 値は $F=0.280$。対象となる F 分布の自由度は $\phi=(15, 13)$ である。有意水準 $\alpha=0.05$ としたとき:

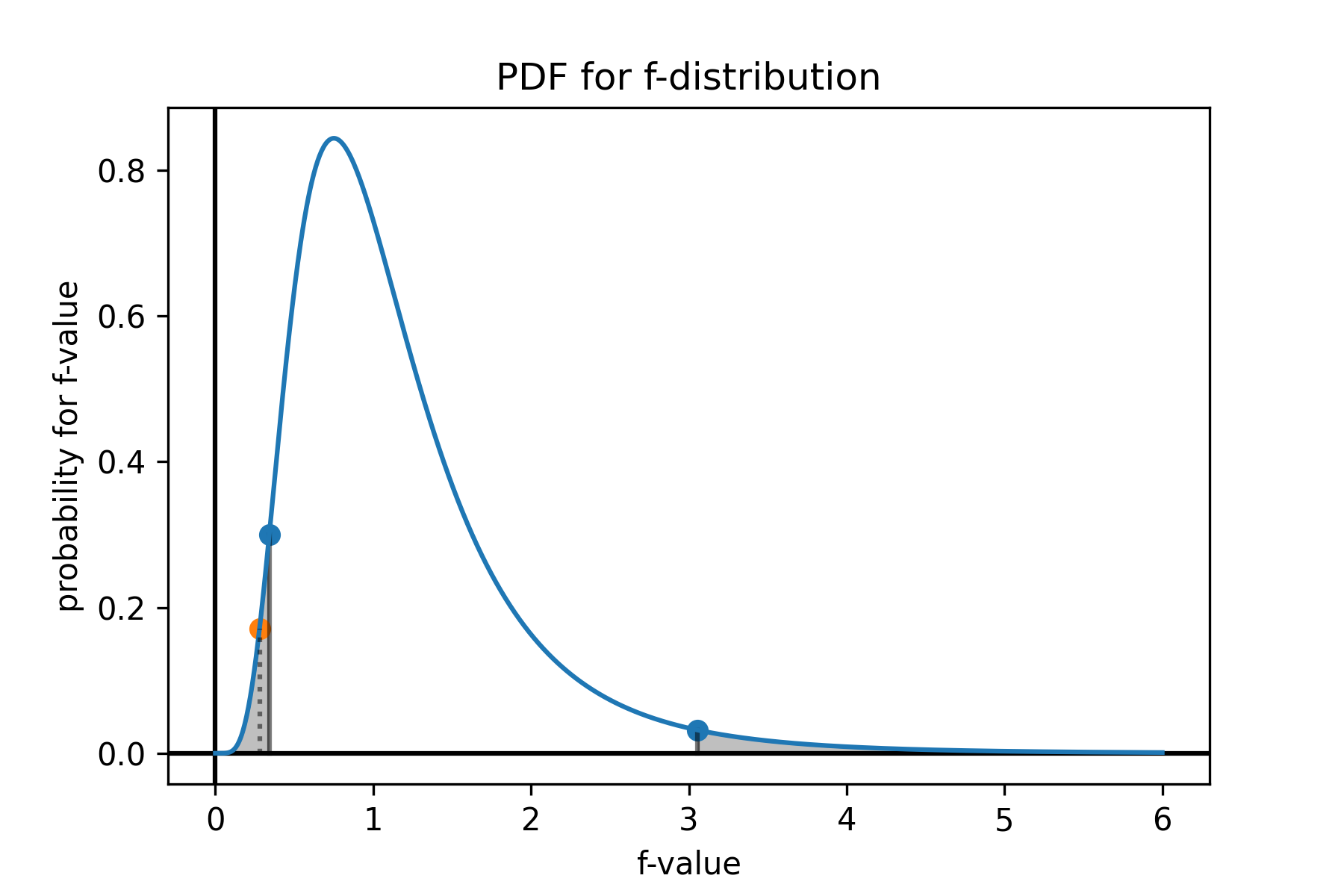
両側検定: 棄却域は $\mathcal{F}_{\phi}^{-1}(\alpha/2)=0.342$ より小さいか $\mathcal{F}_\phi^{-1}(1-\alpha/2)=3.053$ より大きい領域となる。$F$ は棄却域に含まれることから帰無仮説 $H_0:\sigma_x^2=\sigma_y^2$ は棄却され対立仮説 $H_a:\sigma_x^2\ne\sigma_y^2$ を主張することができる。

片側検定 (下側): 棄却域は $\mathcal{F}_{\phi}^{-1}(\alpha)=0.409$ より小さい領域となる。$F$ は棄却域に含まれることから帰無仮説 $H_0:\sigma_x^2=\sigma_y^2$ は棄却され $H_a:\sigma_x^2\lt\sigma_y^2$ であると主張することができる。

片側検定 (上側): 棄却域は $\mathcal{F}_{\phi}^{-1}(1-\alpha)=2.533$ より大きい領域となる。$F$ は棄却域に含まれないことから帰無仮説 $H_0:\sigma_x^2=\sigma_y^2$ は棄却することができず $H_a:\sigma_x^2\gt\sigma_y^2$ であるとは言えない。

以上より、有意水準 $\alpha=0.05$ において新しい温度計 $X$ は以前の温度計 $Y$ よりも値の振れ幅が小さいと主張することができる。
Fig 2. 温度計の分散の差異を計測する両側検定の F 分布。
Notebook
# Jupyter Notebook コード
import scipy.stats
import numpy as np
import matplotlib.pyplot as plt

# μ=27.2, σ=1.3 の正規乱数から抽出した n=16 の標本
x = np.array([26.9, 27.2, 27.6, 28.6, 29.8, 25.4, 26.7, 28.4, 27.0, 26.7, 26.6, 29.0, 27.1, 28.1, 28.1, 27.1])
# μ=27.2, σ=2.2 の正規乱数から抽出した n=14 の標本
y = np.array([25.3, 31.8, 25.4, 26.3, 30.1, 27.7, 27.4, 26.8, 25.7, 29.0, 25.8, 28.2, 24.2, 27.0])

alpha = 0.05

# 統計量の算出
f_dist = scipy.stats.f(len(x)-1, len(y)-1)
f_value = np.var(x, ddof=1) / np.var(y, ddof=1)
print("自由度: φx=%d, φy=%d" % (len(x)-1, len(y)-1))
print("不偏分散: sx=%f, sy=%f" % (np.var(x, ddof=1), np.var(y, ddof=1)))
print("F 値: f=%f" % f_value)
print("有意水準: α=%.2f" % alpha)
print("両側検定: f < %f or f > %f?" % (f_dist.ppf(alpha/2), f_dist.ppf(1-alpha/2)))
print("片側検定: f < %f?" % f_dist.ppf(alpha))
print("片側検定: f > %f?" % f_dist.ppf(1-alpha))

f_values = np.linspace(0, 6, 1000)
pdf_values = f_dist.pdf(f_values)
fill_color = (0, 0, 0, 0.25)
line_color = (0, 0, 0, 0.5)

f0 = f_dist.ppf(alpha / 2)
f1 = f_dist.ppf(1 - alpha / 2)
plt.fill_between(f_values, pdf_values, where=f_values < f0, color=fill_color)
plt.fill_between(f_values, pdf_values, where=f_values > f1, color=fill_color)
plt.plot([f0, f0], [0, f_dist.pdf(f0)], color=line_color)
plt.plot([f1, f1], [0, f_dist.pdf(f1)], color=line_color)

plt.axhline(y=0, color="k")
plt.axvline(x=0, color="k")

plt.plot(f_values, pdf_values)
plt.scatter([f0, f1], [f_dist.pdf(f0), f_dist.pdf(f1)])
plt.plot([f_value, f_value], [0, f_dist.pdf(f_value)], color=line_color, linestyle = "dotted")
plt.scatter([f_value], [f_dist.pdf(f_value)])

plt.xlabel("f-value")
plt.ylabel("probability for f-value")
plt.title("PDF for f-distribution") 
実行結果:
自由度: φx=15, φy=13
不偏分散: sx=1.186958, sy=4.243791
F 値: f=0.279693
有意水準: α=0.05
両側検定: f < 0.341892 or f > 3.052713?
片側検定: f < 0.408478?
片側検定: f > 2.533110?

\(\alpha\)	\(0.01\)	\(0.05\)	\(0.10\)	\(0.20\)	\(p\)
\(H_a:\sigma_x^2 \ne \sigma_y^2 \Leftrightarrow H_0\)
\(H_a:\sigma_x^2 \lt \sigma_y^2 \Leftrightarrow H_0\)
\(H_a:\sigma_x^2 \gt \sigma_y^2 \Leftrightarrow H_0\)

帰無仮説	対立仮説	棄却域
\(H_0:\sigma_x^2 = \sigma_y^2\)	\(H_a:\sigma_x^2 \ne \sigma_y^2\)	\(F \lt \mathcal{F}_\phi^{-1}(\alpha/2)\) または \(F \gt \mathcal{F}_\phi^{-1}(1-\alpha/2)\)
	\(H_a:\sigma_x^2 \lt \sigma_y^2\)	\(F \lt \mathcal{F}_\phi^{-1}(\alpha)\)
	\(H_a:\sigma_x^2 \gt \sigma_y^2\)	\(F \gt \mathcal{F}_\phi^{-1}(1-\alpha)\)

\(F\) 検定

概要

Table of Contents

統計量と確率分布

検定統計量 F

F 分布

F 検定

例1: 温度計の分散比較

参考文献