論文翻訳: Efficient Data Structures for Tamper-Evident Logging

2025年8月2日 2009年の論文 #HistoryTree #MerkleAggregation

Scott A. Crosby
scrosby@cs.rice.edu

Dan S. Wallach
dwallach@cs.rice.edu

Department of Computer Science, Rice University

ABSTRACT

現実世界の多くのアプリケーションは、フォレンジック (forensic) 目的で改ざん証跡ログ (tamper-evident log) を収集したいと考えている。この論文では、信頼できないロガー (untrusted logger) が複数のクライアントにサービスを提供し、これらのクライアントがイベントをログに保存したいと考えている場合を検討する。このロガーは正しい動作を証明するように要求する複数の監査者 (auditors) によって信頼性が保たれている。我々はこの監査プロセスの観点から改ざん証跡ログのセマンティクスを提案する。ロガーは、ここのログイベントがまだ存在していること、そして現在見ているログが過去に見えていたものと一致していることを証明できなければならない。これを効率的に実現するために、我々は対数的なサイズと空間でその証明を生成できるツリーベースのデータ構造について説明する。これは従来の線形構造を改善したものである。従来のハッシュチェーン (hash chain) では、8000 万個のイベントを含むログにおいて、ランダムに選択されたイベントが存在することを証明するために 800MB のトレースが必要になる可能性があるが、我々のプロトタイプでは同じセマンティクスで 3kB の証明を返す。また我々は、ログサーバがある述語 (predicate) に一致するすべてのイベントについて認証済みで改ざん証跡機能を備えた検索結果を提示するための柔軟なメカニズムも提示する。これにより、大規模なログサーバは、合意された方法で古いイベントを選択的に削除しながら、不適切なイベントが駆除されなかったことの効率的な証明を生成できるようになる。我々はプロトタイプ実装について説明し、1 つの CPU コアを使用して 8000 万イベントの syslog トレースで 1 秒あたり 1750 イベントのでの性能を測定した。暗号学的署名 (cryptographic signature) をオフロードすると性能は 1 秒あたり 10,500 イベントに向上し、これは 1 週間あたり 1.1TB のログ処理スループットに対応する。

ABSTRACT
1 導入
2 セキュリティモデル
3 履歴ツリー
4 Merkle 集約
5 Syslog プロトタイプ実装
6 改ざん証跡ログのスケーリング
7 関連研究
8 結論
Acknowledgements
References
翻訳抄

1 導入

米国には、データ保管と管理を規定する規制が 1 万以上存在する [22, 53]。多くの国では法律、金融、医療、教育、プライバシーに関する規制があり、企業は様々な記録の保管を義務づけられている。そのため、ログシステムが広く使用されている (ただし、その多くはセキュリティ機能の面で十分ではない)。

監査ログは、データベースの改ざんの追跡 [59] や、検証可能な監査証跡を持つバージョン管理ファイルシステムの構築 [52] など、様々なフォレンジック目的で有用である。改ざん証跡のあるログは、ビザンチン障害耐性システム [35] やそのプロトコル [15] の構築、分散システムにおける不正な動作をするホストの検出 [29] にも使用されている。

ログの完全性を保証することは大規模システムのセキュリティにおいて重要な要素である。高いアクセス権を持ち、ログ記録システムを破壊できる内部関係者を含む悪意のあるユーザは、ログに記録されない活動を実行したり、記録された履歴を改ざんしたりする可能性がある。このようなシステムの改ざん耐性は不可能かもしれないが、改ざん検出は強固な方法で保証されるべきである。

文献では、ツリー [34, 49]、RSA アキュムレータ [5, 11]、スキップリスト [24]、汎用認証 DAG など、改ざん証跡のある方法でデータを保存するための様々なハッシュデータ構造が提案されている。これらの構造は、証明書失効リスト [49]、改ざん証跡グラフ、幾何検索 [25]、XML クエリーへの認証済み応答 [19] の構築に使用されている。これらはすべて信頼できる作成者 (trusted author) によって作成された静的データを保存し、その署名は検索クエリーへの応答を認証するための信頼ルートとして使用される。

認証付きデータ構造は動的データに適応されているが [2]、信頼できる作成者を前提としているため、バージョン間の不整合を検出する必要がない。例えば SUNDR [36] では信頼できるネットワークファイルシステムが信頼できないストレージ上に実装されている。サーバがフォーク不整合のビューをクライアントに提示したことを検出するためにバージョンベクター [16] が使用されているが、ファイルシステムの更新に署名するのは信頼できるクライアントのみである。

改ざん証跡のあるログは根本的に異なる。信頼できない (untrusted) ロガーがログの唯一の作成者であり、ログの構築と署名の両方に責任を負う。ログは動的なデータ構造であり、作成者はコミットメントのストリームに署名し、新しいイベントがログに追加されるたびに新しいコミットメントが作成される。各コミットメントはその時点までのログ全体のスナップショットである。署名された各コミットメントが認証されたデータ構造のルートである場合、既知の認証付き辞書技術 [62, 42, 20] を用いて各スナップショット内の (within) 改ざんを検出できる。しかし、改ざんを防ぐための追加のメカニズムがなければ、信頼できないロガーは異なるスナップショットに過去についての矛盾した主張 (inconsistent claims about the past) を行わせることができる。安全であるためには、改ざん証跡のあるログシステムは、署名された各ログ内の改ざんを検出し、かつ、ログの異なるインスタンスが矛盾した主張を行っていることも検出しなければならない。

信頼できないサーバが時間の経過と共に矛盾した主張を行っていることを検出するための現在のソリューションは線形空間と線形時間を必要とする。例えば、検出されない改ざんを防止するために、ハッシュチェーンに依存する既存の改ざん証跡ログ [56, 17, 57] では、監査者がスナップショット内のすべての中間イベントを検査する必要がある。改ざん証跡ログに関する一つの提案 [43] はスキップリストに基づいていた。ログが内部的に一貫していると仮定した場合、検索時間は対数的になる。しかし、内部的な一貫性を証明するにはログの内容全体をスキャンする必要がある (これについてのさらなる分析についてはセクション 3.4 を参照)。

同様に、強力な説明責任特性を持つネットワークストレージサービスである CATS [63] は、内部状態のスナップショットを作成し、スナップショット間でオブジェクトのサブセットの正確性を監査することによって確率的にのみ改ざんを検出する。Pavlou と Snodgrass [51] は、改ざん証跡をリレーショナルデータベースに統合する方法を示し、改ざんが疑われる場合にその存在を証明できる。これらのシステムの一貫性を監査することは高コストであり、スナップショット間のすべての変更が承認されていることをかかうにんするために、各監査者が各スナップショットを訪問する必要がある。

信頼できないロガーが、追加されたイベントや返されたコミットメントが監査されないことを知っている場合、追加されたイベントやそのコミットメントによって確定されたイベントでの改ざんは発見されず、定義上、そのログは改ざん証跡があるとは言えない。これを防ぐため、改ざん証跡のあるログには頻繁な監査が必要である。この目的のために、我々はすべての監査および検索操作に対して対数的なツリーベースの履歴データ構造を提案する。ログへのイベント追加、コミットメントの生成、および監査は互いに独立していつでも実行できる。バッチ処理は使用されない。従来の設計とは異なり、我々は監査を通じて改ざんがどのように発見されるかに明確に頂点を宛て、これらの監査コストを最適化する。我々の履歴ツリー (history tree) により、ロガーは時間の経過と共にコミットされた個々のログのシーケンスが過去について一貫した主張をしていることを効率的に証明できる。

セクション 2 では背景資料を示し、改ざん証跡機能を備えたログ記録のセマンティクスを提案する。セクション 3 では履歴ツリーを提示し、セクション 4 ではイベントに属性を付与する Merkle 集約 (Merkle aggregation) について説明する。これにより、ログに対する改ざん証跡クエリーとイベントの安全な削除 (safe deletion) を行うことができ、追加の信頼できる第三者なしに不要なイベントをその場で削除しながら、イベントが不適切に削除されなかったことを証明できる。セクション 5 では syslog データトレースの改ざん証跡のあるログのプロトタイプ実装について説明する。セクション 6 では、ロガーの性能をスケールするためのアプローチについて議論する。関連研究はセクション 7 で示される。今後の研究と結論はセクション 8 で示す。

2 セキュリティモデル

本論文では、攻撃者が電子署名を偽造したり暗号ハッシュ関数の衝突を見つけることは不可能であるという、一般的な暗号学的仮定を前提とする。また、ログに記録されたイベントの機密性保護は考慮しない。これは必要に応じて別途暗号化 [50, 26, 54] などの外部技術によって対処できる。説明を簡潔にするために、単一ホスト上に単一のモノリシックログが存在すると仮定し、我々の目標を改ざんの検出に置く。ビザンチンロガーが管理するデジタル記録の破壊や改ざんを防ぐことは現実的ではないため本稿では扱わないが、可用性を確保する上ではデジタル記録の複製戦略は役に立つだろう [44]。

改ざん証跡には監査が必要である。ログが一度も検査されなければ改ざんを検出することはできない。このため、我々はロギングシステムを 3 つの論理エンティティに分割する。まずログまたは履歴に追加するイベントを生成する多数のクライアントである。クライアントは、中央集権的でありながら全く信頼できないロガーによって管理され、最終的には 1 つ以上の信頼できる監査者によって監査される。クライアントと監査者のストレージ容量は非常に限られているのに対し、ロガーのストレージ容量は無制限であると仮定する。公開されたコミットメントを監査し、証明を要求することで、監査者はログの整合性が維持されていることを確認できる。少なくとも 1 つの監査者は改ざん不可能であると仮定する。我々のシステムではクライアントと監査者を区別するが、実際には単一のホストが両方の役割を担うことも可能である。

クライアントがイベント挿入プロトコルに従っている間は正しく動作すると信頼する必要があるが、それ以外の状況ではクライアントを信用しない。もちろん、悪意のあるクライアントが無意味なデータを挿入する可能性はあるが、一度正しく挿入されたイベントは、その後にクライアントがロガーと結託して改ざんを試みても、検出不能なまま隠蔽・変更されてはならない。

これらのセマンティクスを保証するため、信頼されていないロガーは定期的に監査者やクライアントに対して自身の正しい動作を証明する必要がある。ロガーに要求される増分証明 (incremental proof) は、現在のコミットメントと以前のコミットメントが過去のイベントについて一貫した主張をしていることを証明する。所属証明 (membership proof) は、ロガーに対して、ログ内の指定のイベントを返す際にそのイベントが現在のコミットメントと一致していることを示す証明も要求する。所属証明は、イベントを追加した後にクライアントから要求される場合もあれば、古いイベントがロガーによって正しく保存され続けていることを検証する監査者から要求される場合もある。これら 2 つの証明は改ざん証跡を得るのに十分である。通常の検索操作の後に証明要求が続く可能性があるため、ロガーは忠実に動作しなければならず、さもなければその不正行為が発見されるリスクを負う。

2.1 改ざん証跡のある履歴のセマンティクス

我々はここで安全な履歴に対する望ましいセマンティクスを形式化する。イベント $X$ がロガーに送信されるたびに、ロガーはインデックス $i$ を割り当ててログに追加し、現在までのすべてのイベント $X_0 \ldots X_i$ に依存するバージョン $i$ のコミットメント $C_i$ を生成する。コミットメント $C_i$ はバージョン番号 $i$ にバインドされ、署名され、公開される。

ロガーがコミットする履歴のストリーム $(C_0 \ldots C_i, C_{i+1}, C_{i+1} \ldots)$ は相互に整合しているはずだが、各コミットメントは独立した (independent) 履歴を確定する。履歴が事前に他の履歴と一貫していることは分からないため、我々は異なる履歴とその中に含まれるイベントを区別するためにプライム (') を使用する。言い返れば、ログ $C_i$ 内のイベント (すなわちコミットメント $C_i$ によってコミットされたイベント) は $X_0 \ldots X_i$ であり、ログ $C'_j$ 内のイベントは $X'_0 \ldots X'_i$ である。我々はそれらの対応関係を証明する必要がある。

2.1.1 所属監査

所属監査は、新しいイベントが正しく挿入されていることを検証するクライアントと、古いイベントが依然として存在し変更されていないことを検証する監査者の両方によって実行される。ロガーには、イベントインデックス $i$ とコミットメント $C_j$, $i \le j$ が与えられ、ログの $i$ 番目の要素 $X_i$ と、$C_j$ が $X_i$ のログの $i$ 番目のイベントであることを示唆するという証拠を返す必要がある。

2.1.2 増分監査

検証された所属証明は、あるイベントがそのコミットメント $C_j$ によって表されるある (some) ログに正しく記録されたことを示すが、ロガーによってコミットされたログのシーケンスが事件の経過と共に一貫していることを検証するには追加の作業が必要である。増分監査では、ロガーに $j \le k$ となるような 2 つのコミットメント $C_j$ と $C'_k$ が与えられ、これらの 2 つのコミットメントが過去のイベントについて一貫した主張をしていることを証明する必要がある。検証された増分証明は、すべての $a \in [0,j]$ に対して $X_a = X'_a$ であることを示す。一度検証されると、監査者は $C_j$ と $C'_k$ が同じ共有履歴にコミットされていることを知り、$C_j$ を安全に破棄できる。

不正なロガーはログをロールバックして新しいフォークを作成し、そこに新しいイベントを挿入して古いフォークを破棄することで、履歴を改ざんしようとする可能性がある。このような改ざんは、ログシステムが履歴一貫性 (historical consistency) を満たしている場合 (セクション 2.3 参照) と、ロガーは要求されたときに異なるフォーク (矛盾するフォーク) 上のコミットメント間で増分証明を生成できないという条件によって検出される。

2.2 クライアント挿入プロトコル

クライアントがイベント挿入後にロガーからコミットメントを受け取ると、直ちにそれらを監査者に再送付しなければならない。これにより、クライアントが後でロガーと共謀してイベントをロールバックしたり変更したりすることを防ぐ。このためには、クライアントからの署名済みコミットメントを複数の監査者に配布するために、ゴシッププロトコルなどのメカニズムを必要とする。すべての監査者がすべてのコミットメントを監査する必要はなく、いずれかの監査者がすべてのコミットメントを監査する限り十分である (他の監査戦略とのトレードオフについてはセクション 3.1 でさらに議論する)。

さらに、ロガーが異なる監査者やクライアントに異なるログのビューを提示することに対処するために、監査者は複数のクライアントや監査者から受信したコミットメントを取得し、調整する必要がある。これには前述のゴシッププロトコルなどが使用される可能性がある。あるいは、ロガーがコミットメントを公開形式で発行紙、すべての監査者が同じコミットメントを受け取るようにすることもできる [27]。重要なのは、監査者が多様なコミットメントの集合にアクセスでき、ロガーが一貫したビューを提示していることを検証するために増分証明を要求できることである。

2.3 定義: 改ざん証跡履歴

ここで我々は改ざん証跡履歴システム (tamper-evident history system) を以下の 5 つのアルゴリズムの組として定義する:

$H.{\rm Add}(X) \to C_j$. イベント $X$ が与えられた場合、それを履歴に追加し、新しいコミットメントを返す。
$H.{\rm Incr}.{\rm Gen}(C_i,C_j) \to P$. $i \le j$ に対して $C_i$ と $C_j$ 間の増分証明を生成する。
$H.{\rm Membership}.{\rm Gen}(i,C_j) \to (P,X_i)$. $i \le j$ に対してコミットメント $C_j$ からイベント $i$ の所属証明を生成する。またイベント $X_i$ も返す。
$P.{\rm Incr}.{\rm Vf}(C'_i,C_j) \to \{\top,\bot\}$. $i \le j$ に対して $C_j$ が $C'_i$ によって確定されたすべてのエントリを確定することを $P$ が証明するかどうかを検証する。分岐 (divergence) が検出されなければ $\top$ を出力する。
$P.{\rm Mmembership}.{\rm Vf}(i,C_j,X'_i) \to \{\top,\bot\}$. $i \le j$ に対して、イベント $X'_i$ が $C_j$ によって定義されるログ内の $i$ 番目のイベントであることを $P$ が証明するかどうかを検証する。true であれば $\top$ を出力する。

最初の 3 つのアルゴリズムはロガー上で実行され、ログ $H$ への追加と証明 $P$ の生成に使用される。監査者またはクライアントはアルゴリズム $\{{\rm Incr.Vr}$, ${\rm Membership.Vf}\}$ を使用して証明を検証する。理想的には、監査者に送信される証明 $P$ は完全な履歴 $H$ を再送信するよりも簡潔である。ロガーによって署名される必要があるのはコミットメントのみである。証明にはデジタル署名は必要ではなく、コミットメントとイベントの内容の一貫性を示すか、示さないかのいずれかである。これら 5 つの操作により "改ざん証跡" (tamper evidence) を以下の条件を満たすシステムとして定義する。

履歴一貫性 (historical consistency). $j \le k$ において、2 つのコミットメント $C_j$ と $C_k$ 間に有効な増分証明があり ($P.{\rm Incr.Vf}(C_j,C_k) \to \top$)、$C_j$ によって確定されるログ内のイベント $X'_i$ の有効な所属証明 $P'$ があり (つまり $P'.{\rm Membership.Vf}(i,C_k,X''_i) \to \top$)、そして $C_k$ によって確定されるログ内の $X''_i$ について有効な所属証明がある場合 (つまり $P''.{\rm Membership.Vf}(i,C_k,X''_i) \to \top$)、$X'_i$ は $X''_i$ と等しくなければならない。(言い換えると、2 つのコミットメントが一貫性のある履歴をコミットする場合、それらは両方とも要求された過去について同じイベントを確定しなければならない)。

2.4 その他の脅威モデル

前方整合性 (forward integrity). 従来の改ざん証跡ログは前方整合性 [4] という異なる脅威モデルを使用する。前方整合性脅威モデルには 2 つのエンティティがある。一つは完全に信頼されているものの限られたストレージを持つクライアント、もう一つはビザンチン障害が発生するまで誠実であると想定されるロガーである。この脅威モデルでは、ロガーはビザンチン障害発生前に記録されたイベントをケ位置不可能な方法で改ざんすることを防止する必要があるが、ビザンチン障害発生後に記録されたイベントを検知不能な方法で改ざんすることは許可されている。

我々の脅威モデルは改ざん証跡ログが直面する脅威をよりより適切に特徴付けていると考えているが、我々の履歴ツリーと改ざん証跡ログのセマンティクスはわずかな変更を加えるだけでこの代替の脅威モデルにも適用可能である。前方整合性のセマンティクスでは改ざん証跡はビザンチン障害以前に発生したイベントにのみ適用されるため、追加されたばかりのイベントの所属監査は不要である。ビザンチン障害が発生していない場合、追加されたばかりのイベントの監査は不要であり、ビザンチン障害発生後には無関係である。それでも増分監査は依然として必要である。クライアントは、受信したコミットメントを増分的に監査する必要がある。これは、ログをロールバックして新しいフォークを生成することで、ロガーがビザンチン障害以前に発生したイベントを改ざんするのを防ぐためである。所属監査は、ログ内の古いイベントを検索して調査するために必要である。

Itkis [31] も同様の脅威モデルを持っている。彼の設計はビザンチンロガーがビザンチン障害以前の履歴をロールバックするには、履歴が 2 つの並列履歴にフォークするという事実を利用している。彼は、ロガーとオンラインインタラクションなしに 2 つのコミットメントをテストする手順を提案し、コミットメントサイズの下限が $O(n)$ であることを証明した。我々は、ロガーがこれらの証明の生成に協力することでより厳しい下限を実現している。

信頼できるハードウェア (trusted hardware). 監査に依存するのではなく、ロガーのハードウェア自体が耐タンパー性を持つことに依存する代替モデルもある [58, 1]。当然ながら、これらのシステムのセキュリティは、完全な物理的アクセスを持つ攻撃者による改ざんから信頼できるハードウェアとログシステムを保護することにかかっている。我々の設計は確実に信頼できるハードウェアを監査装置として使用することも可能であるが、我々のような暗号学的スキームはより単純な仮定、すなわちロガーが正しく動作していることを証明でき、かつ証明しなければならないという仮定に基づいている。

3 履歴ツリー

ここで我々は改ざん証跡履歴を表現するための新しいデータ構造を提示する。我々はまず、静的データを認証するために長年利用されてきた Merkle ツリー [46] を取り上げる。Merkle ツリーでは、データは葉に格納され、ルートのハッシュはその内容の改ざん証跡要約である。Merkle ツリーは根から葉への対数的パス長をサポートし、効率的なランダムアクセスを可能にする。Merkle ツリーはよく知られた改ざん証跡データ構造であり、本研究での使用も直接的であるが、我々の設計における新規性は、Merkle ツリー状のハッシュのバージョン計算を用いることで、異なる (distinct) ルートハッシュを持つ Merkle ツリーで表される異なるログスナップショットが、過去について一貫した主張をしていることを効率的に証明することである。

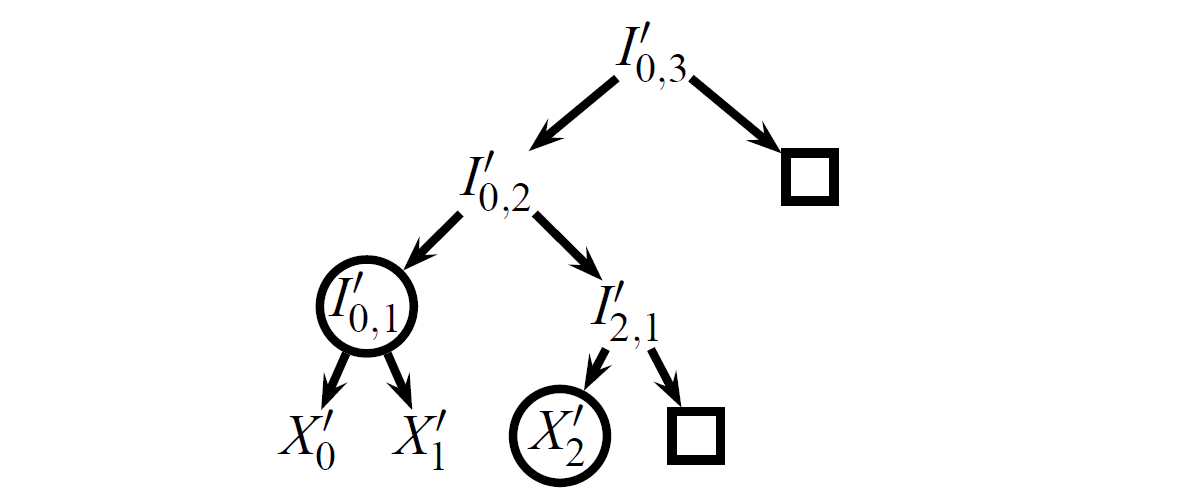
深さ $d$ の満たされた履歴ツリーは、葉に $2^d$ 個のイベントを保持する Merkle ハッシュツリーである。内部ノード $I_{i,r}$ はインデックス $i$ と層 $r$ で識別される。層 0 にある各葉ノード $I_{i,0}$ はイベント $X_i$ を格納する。内部ノード $I_{i,r}$ は、左の子 $I_{i,r-1}$ と右の子 $I_{i+2^{r-1},r-1}$ を持つ (Figure 1 から Figure 3 がこの番号付けスキームを示している)。ツリーが満たされていない場合、イベントを含まない部分木は $\square$ として表現される。これは、Figure 1 に示されている 3 つのイベントを持つバージョン 2 ツリーから見ることができる。Figure 1 は 4 角イベントを追加したバージョン 6 のツリーを示している。図のツリーは深さ 3 を持ち最大 8 個の葉を保存できるが、この設計がより深くより多くの葉を持つツリーにも拡張できることは明らかである。

履歴ツリーの各ノードには、Merkle ツリーと同様に、そのノードをルートとする部分木の内容を確定する暗号学的ハッシュでラベル付けされている。葉ノードに対してラベルはイベントのハッシュであり、内部ノードに対してラベルはその子ノードのラベルを連結したハッシュである。

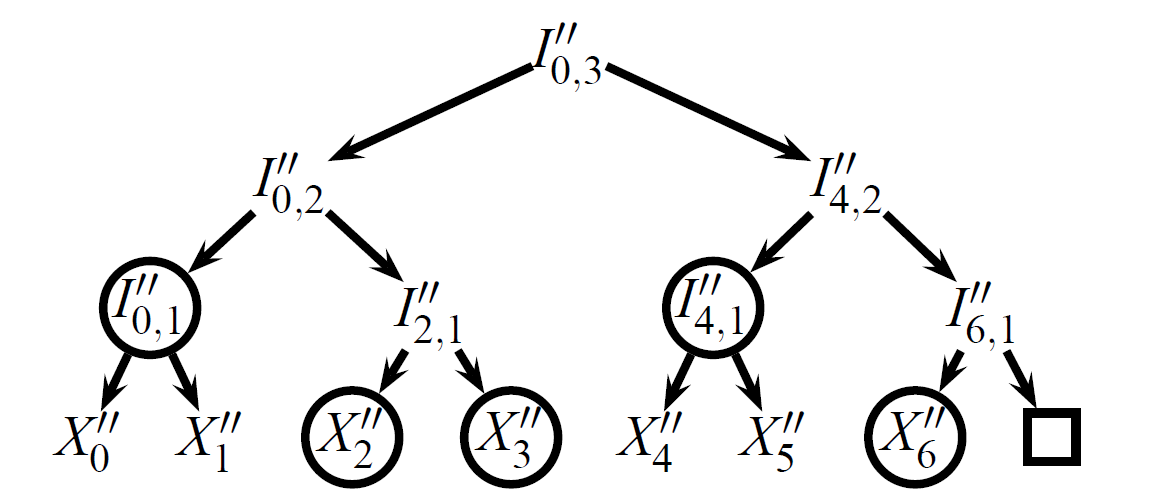
履歴ツリーの興味深い性質は、ツリーの古いバージョンまたはビューを効率的に再構築する能力である。Figure 2 に示す履歴ツリーについて考えると、ロガーはノード $I''_{4,2}$ と $X''_3$ が $\bot$ であると仮定し、内部ノードとルートのハッシュを再計算することによって Figure 1 のバージョン 2 ツリーに類似した $C''_2$ を再構築できる。再構築された $C''_2$ が以前に公表されたコミットメント $C'_2$ と一致した場合、両方のツリーは同じ内容を持ち、同じイベントをコミットしていなければならない。

Figure 1: コミットメント $C'_2 = I'_{0,3}$ を持つバージョン 2 履歴。

Figure 2: コミットメント $C''_6 = I''_{0,3}$ を持つバージョン 6 履歴。

Figure 3: バージョン 2 とバージョン 6 の間の増分証明 $P$。丸で囲んだノードのハッシュは証明に含まれる。他のハッシュはその子ノードから導出できる。Figure 1 と Figure 2 の丸で囲んだノードは、ここで対応する丸で囲んだノードと等しいことを示さなければならない。

Figure 4: Figure 3 に示した証明と対応する履歴ツリーの図式表記。塗りつぶされた円は証明に含まれるハッシュを表しており、それ以外のノードは証明には含まれない。ドットおよび白抜きの円はそれぞれ下位の値から再計算可能なノードを示す。ドットは新しいイベントが追加されると値が変化する可能性があるのに対し、白抜きの円は変化しない。灰色の円は証明に不要なノードを表す。

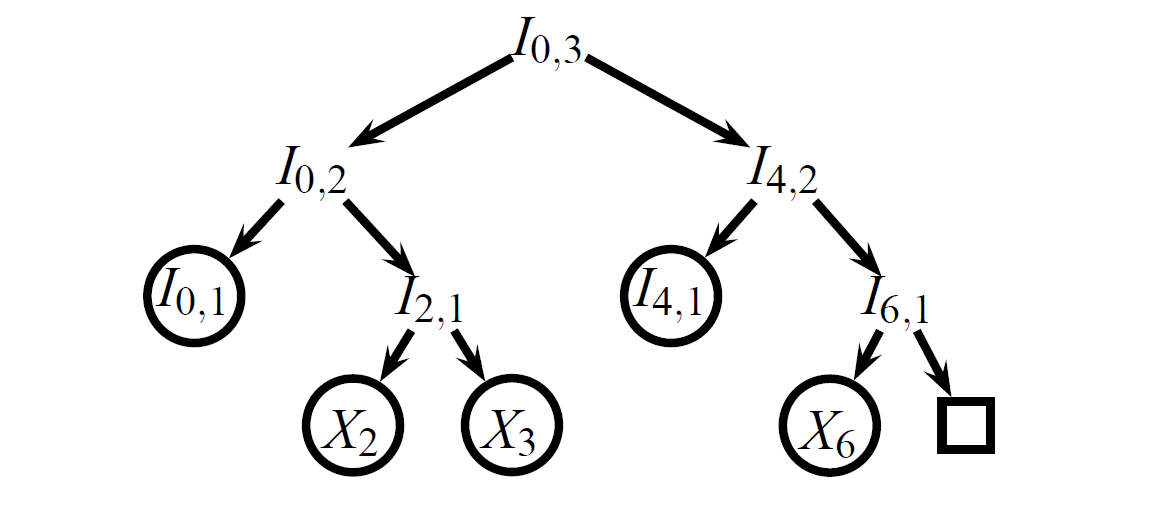
これは、ロガーが 2 つのコミットメント $C'_2$ と $C''_6$ 間の増分証明 $P$ を生成する方法の直感を形成する。最初、監査者はコミットメント $C'_2$ と $C''_6$ のみを所有しており、これらのコミットメントが確定する根底となる Merkle ツリーを認識していない。ロガーは、両方の履歴が同じイベントをコミットすること、つまり $X''_0 = X'_0$, $X''_1 = X'_1$, $X''_2 = X'_2$ をであることを示さなければならない。これを行うために、ロガーは Figure 3 に示すように剪定されたツリー (pruned tree) $P$ を監査者に送信する。この剪定ツリーにはコミットメント $C_2$ と $C_6$ を計算するのに十分な完全履歴ツリーの部分のみが含まれている。不要な部分木は省略されスタブで置き換えられる。イベントはツリーに含まれるか、そのハッシュを含むスタブで置き換えられる。増分証明には 3 つの履歴ツリー、つまり $C'_2$ と $C''_6$ によってコミットされた未知のツリーと剪定ツリー $P$ を含むため、我々は異なる数のプライム記号 (') を使用してそれらを区別する。

Figure 3 に示す $P$ から、我々はバージョン 6 のツリー $C_6$ に対応するルートコミットメントを再構築する。子ノードのハッシュに基づいて内部ノードのハッシュを再計算し、ノード $I_{0,3}$ のハッシュを計算する。これがコミットメント $C_6$ となる。$C''_6 = C_6$ の場合、Figure 2 および Figure 3 で丸で囲まれた剪定ツリー $P$ と $C''_6$ によってコミットされた暗黙のツリーが一致しなければならない。

同様に、Figure 3 に示す $P$ からノード $X_3$ と $X_4$ が $\square$ であると仮定し、以前と同様に内部ノードのハッシュをルートまで再計算することによって、バージョン 2 のコミットメント $C_2$ を再構築できる。$C'_2 = C_2$ であれば、Figure 1 と Figure 3 で丸で囲まれた、剪定ツリー $P$ と $C'_2$ によってコミットされた暗黙のツリーに対応するノードは一致しなければならない、つまり $I'_{0,1} = I_{0,1}$ かつ $X'_2 = X_2$ となる。

$C'_2$ と $C''_6$ によってコミットされたイベントが $P$ によってコミットされたイベントと同じである場合、それらは等しくなければならない。したがって $C''_6$ によってコミットされたツリーが $C'_2$ によってコミットされたツリーと整合していると結論づけることができる。これは、$C'_2$ と $C''_6$ によってコミットされた履歴ツリーが両方とも同じイベント、すなわち $X''_0 = X'_0$, $X''_1 = X'_1$, $X''_2 = X'_2$ をコミットすることも意味する。これは、イベント $X''_0 = X'_0$, $X''_1 = X'_1$, $X''_4$, $X''_5$ が監査者には未知であってもである。

3.1 監査中にノードをスキップしても安全か?

Figure 3 の剪定ツリーでは、我々は $I_{0,1}$ によって確定されたイベントを省略するが、それでも改ざん証跡ログのセマンティクスを保持する。これらの以前のイベントは監査者に送信されないかもしれないが、ツリー内でそれらの上にある変更されていないハッシュによって依然として確定されている。改ざんの試みは、スキップされたイベントの将来の増分または所属監査で発見される。履歴ツリーを使用すると、監査者は監査することを選択したイベントを監査するために必要な履歴の部分のみを受信する。イベントをスキップすることで様々な選択的監査を実施できるようになり、監査ポリシーの設計においてより高い柔軟性を提供する。

従来のハッシュチェーンに基づく既存の改ざん証跡ログ設計は、$C_i = H(C_{i-1}\,||\,X_i)$, $C_{-1} = \square$ の形式を持ち、イベントのスキップは許可されていない。ハッシュチェーンでは、2 つのコミットメント間、またはイベントとコミットメント間の増分証明または所属証明には、ログ内のすべての中間イベントを含める必要がある。さらに、中間イベントをスキップできないため、監査者として動作する各監査者または各クライアントは、最終的にログ内のすべてのイベントを受信しなければならない。ハッシュチェーンスキーム自体は、イベント量が少ない場合、またはすべての監査者が既にすべてのイベントを受信している状況でのみ実現可能である。

所属証明を使用して古いイベントを調査する場合、ノードをスキップできることで証明サイズを劇的に削減できる。例えば、セクション 5 で説明される我々のプロトタイプでは、8000 万イベントのログにおいて、我々の履歴ツリーはランダムに選択された任意のイベントについて完全な証明を 3100 バイトで返すことができる。中間イベントをスキップできないハッシュチェーンでは平均 4000 万ハッシュが送信される。

監査戦略 (auditing storategies). 多くの設定において、すべての監査者がログに記録されているすべてのイベントに興味を持つとは限らない。クライアントは、他のクライアントによって挿入されたイベントは受信されたコミットメントの監査に興味がないかもしれない。単一のロガーが多くの組織間で共有され、各組織は自身のデータの整合性のみの監査に同期づけられるシナリオは容易に想像できる。これらの組織は独自に監査ツールを運用し、自身のクライアントからのコミットメントに焦点を絞り、フォークが発生していないことを確認するために時折他の組織とのコミットメントを交換するといった運用も可能である。また、独立系会計事務所が企業顧客のログサーバに対して監査システムを運用するシナリオも考えられる。

クライアントがロガーから受信したコミットメントを少なくとも 1 つの誠実な監査者にゴシップ誌、監査者がそれを増分証明の要求時に使用すれば、ログの改ざん証跡は維持されている。すべてのコミットメントをすべての監査者が監査する必要がないため、すべての監査者による監査オーバーヘッドの合計は、ログ内のイベントの総計に比例する。これは、要求されるイベント数 × 監査者の数よりもはるかに安価である。

ノードをスキップすることで、時間とセキュリティに関する他のトレードオフが生じる。監査者は受信したコミットメントの一部のみを監査対象として確率的に監査を実施することができる。ロガーが定期的にログを改ざんした場合、改ざんが検知されない確率は極めて小さくなる。

3.2 履歴ツリーの構築

ツリーベースの履歴の使用方法の例が示されたので、我々はその構築とセマンティクスを正式に定義する。バージョン $n$ の履歴ツリーには、$n+1$ 個のイベント $X_0 \ldots X_n$ を保存する。ハッシュは、履歴ツリー全体にわたって古いバージョンまたはビューの内部ノードのハッシュを再構築できるような方法で計算される。我々は、ノード $I_{i,r}$ のハッシュを $A_{i,r}^v$ で表す。これは計算対象のノードのインデックス、層、およびビューによってパラメータ化される。バージョン $n$ の履歴ツリーにおけるバージョン $v$ のビューは、イベント $X_0 \ldots X_v$ のみを含むバージョン $v$ の履歴ツリーの内部ノードのハッシュを再構築する。$v = n$ の場合、再構築されたルートコミットメントは $C_n$ である。ハッシュは Figure 5 で定義された再帰式を使用して計算される。

\[ \begin{eqnarray} A_{i,0}^v & = & \left\{ H(0\,||\,X_i) \right. \quad \text{if $v \ge i$} \label{eq1} \\ A_{i,r}^v & = & \left\{ \begin{array}{ll} H(1\,||\,A_{i,r-1}^v\,||\,\square) & \quad \text{if $v \lt i+2^{r-1}$} \\ H(1\,||\,A_{i,r-1}^v\,||\,A_{i+2^{r-1},r-1}^v) & \quad \text{if $v \ge i+2^{r-1}$} \end{array} \right. \label{eq2} \\ C_n & = & A_{0,d}^n \label{eq3} \\ A_{i,r}^v & \equiv & {\rm FH}_{i,r} \quad \text{whenever $v \ge i+2^r-1$} \label{eq4} \end{eqnarray} \]

Figure 5: ハッシュを計算するための再帰。

履歴ツリーは木がいっぱいになったとき (すなはち $n=2^d-1$) に深さを増やし、$d = \lceil\log_2(n+1)\rceil$ と定義することによって、任意のサイズのログをサポートできる。1 レベル上の新しいルートは古いツリーを左の子とし、新しいイベントを追加できる空の右の子とともに作成される。我々の説明と証明を簡潔にするため、固定の深さ $d$ のツリーを仮定する。

履歴ツリー内の特定の部分木が完成し、イベントを追加するためのスロットがなくなると、その部分木のルートノードのハッシュは凍結され、今後イベントがログに追加されても変更されない。ロガーは、これらの凍結されたハッシュ (つまり凍結されたノードのハッシュ) を ${\rm FH}_{i,r}$ にキャッシュし、再計算の必要性を回避する。この凍結されたハッシュキャッシュを利用することでロガーは任意のノードの $A_{i,r}^v$ を最大 $O(d)$ 回の演算で再計算できる。バージョン $n$ のツリーでは、$n \ge i+2^r-1$ のときにノード $I_{i,r}$ が凍結される。ログに新しいイベントを挿入すると、期待値 $O(1)$、最悪ケースでは $O(d)$ のノードが凍結される。(Figure 1 ではノード $I'_{0,1}$ が凍結されている。イベント $X_3$ が追加されると、ノード $I'_{2,1}$ と $I'_{0,2}$ が凍結される。)

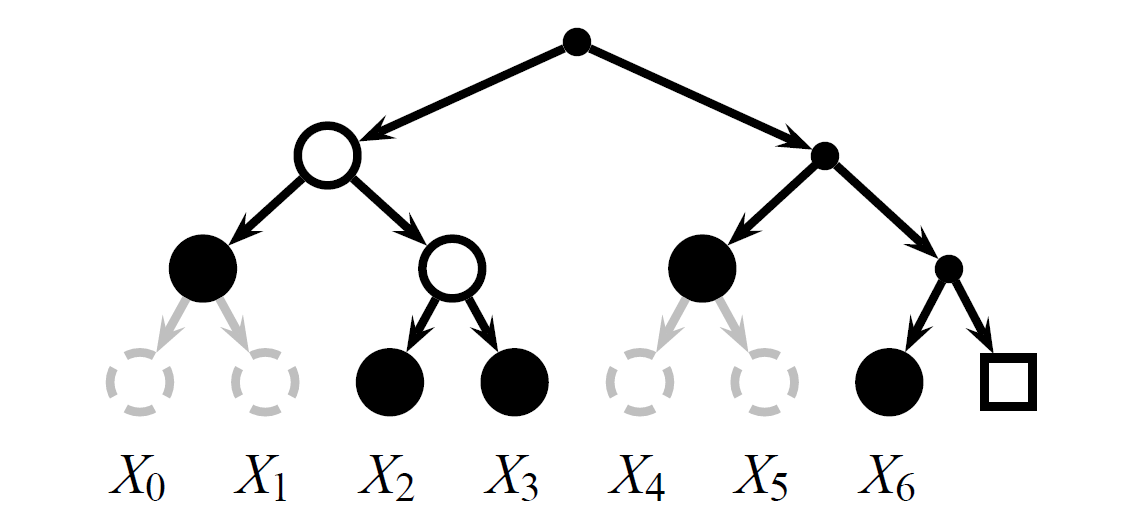
これで履歴ツリーを定義したので、我々はロガーによって生成される増分証明について説明する。Figure 4 は $C_2$ から $C_6$ への増分証明を表す、Figure 3 で与えられた証明と等価な剪定ツリーを抽象的に示している。ドットはハッシュがその子ノードから計算される非凍結ノードを表す。白い丸はハッシュがその子ノードから再計算できるため証明に含まれない凍結ノードを表す。黒い丸は、葉またはスタブであるため証明に含める必要のある凍結ノードを表す。灰色のノードは剪定ツリーに含まれない省略された部分木を表す。この剪定ツリーと (Figure 5 に示す) 式 ($\ref{eq1}$)-($\ref{eq4}$) から $C_6 = A_{0,3}^6$ であり、かつ以前のバージョン 2 のビューからコミットメント $A_{0,3}^2$ を計算できる。

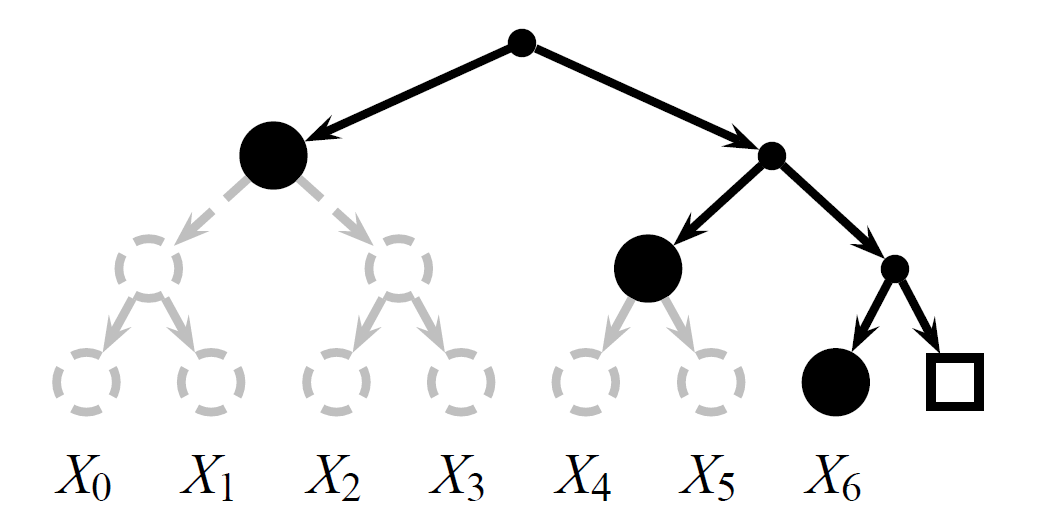
この剪定ツリーは Figure 6 に見られる証明スケルトン (proof skeleton)、つまり凍結ノードのみで構成されるバージョン 6 ツリーの最小剪定ツリーから増分的に構築される。バージョン $n$ ツリーの証明スケルトンは $X_n$ からルートへの経路の左兄弟の凍結ハッシュで構成される。含まれているハッシュと式 ($\ref{eq1}$)-($\ref{eq4}$) を用いることで、この証明スケルトンは $C_6 = A_{0,3}^6$ を算出するのに十分である。

Figure 6 から、ロガーは凍結された内部ノードを分割することで Figure 4 を増分的に構築する。ノードは、自身ではなくその子ノードのハッシュを剪定ツリーに含めることによって分割される。葉への経路上のノードを再帰的に分割することにより、ロガーはその葉を剪定ツリーに含めることができる。この例ではノード $I_{0,2}$ と $I_{2,1}$ を分割する。増分証明で再構築可能な各コミットメント $C_i$ について、剪定ツリー $P$ はイベント $X_i$ への経路を含んでいなければならない。同じアルゴリズムがイベント $X_i$ の所属証明を生成するためにも用いられる。

これらの制約を前提として、我々は Figure 5 の式を用いて 5 つの履歴操作を定義できる。

$H.{\rm Add}(X) \to C_n$. イベントは次の空きスロット $n$ に割り当てられる。$C_n$ は式 ($\ref{eq1}$)-($\ref{eq4}$) によって算出される。
$H.{\rm Incr.Gen}(C_i,C_j) \to P$. 剪定ツリー $P$ は $X_i$ への経路を含むバージョン $j$ の証明スケルトンである。
$H.{\rm Membership.Gen}(i,C_j) \to (P,X_i)$. 剪定ツリー $P$ は $X_i$ への経路を含むバージョン $j$ の証明スケルトンである。
$P.{\rm Incr.Vf}(C''_i,C'_j) \to \{\top,\bot\}$. $P$ から式 ($\ref{eq1}$)-($\ref{eq4}$) を適用して $A_{0,d}^i$ と $A_{0,d}^j$ を計算する。これは、$P$ が葉 $X_i$ への経路を含む場合にのみ実行できる。$C''_i = A_{0,d}^i$ かつ $C'_j = A_{0,d}^j$ の場合 $\top$ を返す。
$P.{\rm Membership.Vf}(i,C'_j,X'_i) \to \{\top,\bot\}$. $P$ から式 ($\ref{eq1}$)-($\ref{eq4}$) を適用して $A_{0,d}^j$ を計算する。また剪定ツリー $P$ から $X_i$ を抽出する。これは、$P$ がイベント $X_i$ へのパスを含む場合にのみ実行できる。$C'_j = A_{0,d}^j$ かつ $X_i = X'_i$ の場合 $\top$ を返す。

増分証明と所属証明は異なるセマンティクスを持つが、両方とも同一のツリー構造に従い、共通の実装によって構築および監査できる。さらに、単一の剪定ツリー $P$ に複数の葉への経路を埋め込むことで複数の監査要求を満たすことができる。

証明として使用される剪定ツリーのサイズはどの程度か? $C_i$ と $C_j$ 間の自己完結的な増分証明、または $C_j$ 内の $i$ の所属証明を満たすのに必要な剪定ツリーには、ノード $X_i$ と $X_j$ へのパスが含まれている必要がある。この結果として得られる剪定ツリーは最大 $2d$ 個の凍結ノードが含まれている。

実際の実装では、ログはより後のバージョン $k$ に進んでいる可能性がある。監査者が $C_i$ と $C_j$ 間の増分証明を要求した場合、ロガーは最新のコミットメント $C_k$ と、$X_i$ と $X_j$ への経路を含むバージョン $k$ のツリーに基づく最大 $3d$ 個のノードからなる剪定ツリーを返す。より一般的には、監査者はコミットメント $C_i$ と最新コミットメント間の増分証明を要求すると想定される。ロガーは、最新のコミットメント $C_k$ と、$X_i$ への経路を含む最大 $2d$ 個のノードからなる剪定ツリーで応答できる。

凍結ハッシュキャッシュ. 履歴ツリーの説明において、ロガーが履歴ツリー内のすべての凍結された内部ノードの凍結ハッシュを保存すると述べ、完全な表現について説明した。このキャッシュは、ノードのハッシュがその子ノードから再計算できる場合は冗長である。監査やクエリーのために剪定ツリーを構築するロガー実装は、効率を改善するためにキャッシュを維持・使用すると想定される。

所属証明、増分証明、クエリー検索結果を生成する際、内部ノードのハッシュがその子ノードから再計算できる場合、結果として得られる剪定ツリーに冗長なハッシュを含める必要はない。証明として使用される剪定ツリーは、通信コストを削減するために、スタブの凍結ハッシュのみを含むこの最小限の表現を使用すると想定される。

証明間の冗長性を利用してオーバーヘッドを削減できるか? 監査者がロガーと定期的に通信し、以前のコミットメントと最新のコミットメント間の増分証明を要求する場合、連続するクエリーの剪定された部分木間に冗長性が生じる。

監査者が以前に $C_i$ と $C_j$ 間の増分証明を要求し、その後 $C_j$ と $C_n$ 間の増分証明 $P$ を要求した場合、2 つの証明は葉 $X_j$ への経路上のハッシュを共有する。ロガーはこれらの共通ハッシュを省略し、$X_j$ と $X_n$ への経路間で共有されない期待値 $O(\log_2(n-j))$ 個の凍結ハッシュのみを含む部分証明 (partial proof) を送信できる。挿入のたびに証明を要求する場合、これは $O(1)$ に退化する。監査者はこれを機能させるために $d$ 個の凍結ハッシュをキャッシュするだけで良い。

ツリー履歴タイムスタンプサービス. 我々の履歴ツリーは、ラウンドベースのタイムスタンプサービスを実装するように適応できる。すべてのラウンドの終了後、ロガーは最後のコミットメントを新聞などの公開媒体で公開する。前ラウンドのコミットメントを $C_i$、クライアントが文書 $X_j$ にタイムスタンプを付与する要求を行ったラウンドのコミットを $C_k$ とする。クライアントは、葉 $X_i$, $X_j$, $X_k$ への経路を含む剪定ツリーを要求できる。剪定ツリーは、ロガーの協力なしに、公開されているコミットメントと照合することで $X_j$ がそのラウンドで提出されたこと、および、そのラウンド内での順序を証明できる。

各ラウンドに対して別々の履歴ツリーが構築される場合、我々の履歴ツリーは、タイムスタンプシステム向けに Buldas ら [10] が提案したスレッド認証ツリーと等価となる。

3.3 二次記憶装置へのログの保存

我々の履歴ツリーは興味深い特性を提供する。それは一度だけ書き込み可能な追加専用ストレージ (write-once append-only storage) に容易にマッピングできることである。ノードが凍結されると、それらは不変となり、安全に出力できる。この順序は事前に決定されており、$(X_0)$, $(X_1,I_{0,1})$, $(X_2)$, $(X_3,I_{2,1},I_{0,2})$, $(X_4) \ldots$ のように開始できる。括弧は各 ${\rm Add}$ トランザクションによって書き込まれるノードを示している。各グループ内のノードがツリー内のレイヤーによってさらに順序付けされている場合、この順序は単純に二分木の後順走査である。このように線形に書き込まれるデータは、ディスクシークのオーバーヘッドを最小限に抑え、ディスクへの書き込みパフォーマンスを向上させる。このレイアウトで、すべてのイベントがディスク上で同じサイズであると仮定すると、(index, layer) からそのノードを格納するために使用されるバイトインデックスへの変換は $O(\log n)$ 回の算術演算で済み、効率的な直接アクセスが可能になる。

可変長イベントを処理するためには、イベントデータは別の追記専用値ストレージ (value storage) に保存でき、履歴ツリーの葉はイベント内容が格納されている値ストアへのオフセットが格納される。履歴ツリーと値ストアを分離することで、イベントの格納方法に関して、データベース、圧縮ファイル、標準的なフラット形式など、多様な選択肢も可能になる。

3.4 他のシステムとの比較

このセクションでは、我々の履歴ツリーと従来のハッシュチェーンおよびスキップリスト構造の間の時間と空間のトレードオフを評価する。3 つの設計すべてにおいて、所属証明は増分証明と同じ構造とサイズを持ち、証明はそのサイズに比例した時間で生成される。

Maniatis と Baker [43] は、スキップリスト [53] の決定論的変種を飼養した改ざん証跡ログを提示している。スキップリストの履歴は、多くのノードを飛び越える追加のスキップリンクを組み込んだハッシュチェーンのようなもので、対数的な検索を可能にする。

Table 1: イベントをログに追加する時間と、生成される完全証明と部分証明のサイズを、ログ内のイベント数 $n$ で特徴付ける。部分証明の監査では、$j$ は最後の監査時のログ内のイベント数を表し、$i$ は所属監査されるイベントのインデックスを表す。
	ハッシュチェーン	スキップリスト	履歴ツリー
${\rm Add}$ 時間	$O(1)$	$O(1)$	$O(\log_2 n)$
$C_k$ の ${\rm Incr.Gen}$ 証明サイズ	$O(n-k)$	$O(n)$	$O(\log_2 n)$
$X_k$ に対する ${\rm Membership.Gen}$ 証明サイズ	$O(n-k)$	$O(n)$	$O(\log_2 n)$
キャッシュサイズ	-	$O(\log_2 n)$	$O(\log_2 n)$
${\rm Incr.Gen}$ 部分証明サイズ	-	$O(n-j)$	$O(\log_2(n-j))$
${\rm Membership.Gen}$ 部分証明サイズ	-	$O(\log_2 (n-j))$	$O(\log_2 (n-j))$

Table 1 で我々は 3 つの設計を比較する。3 つの設計はすべて、イベントあたりのストレージ容量が $O(1)$、コミットメントサイズが $O(1)$ である。部分証明 (セクション 3.2 参照) をサポートするスキップリスト履歴とツリー履歴について、我々はログ内のイベント数 $n$、ロガーと以前のコンタクトのインデックス $j$、または検索対象のイベントインデックス $i$ に基づいて、キャッシュサイズと期待される証明サイズを示す。我々のツリーベース履歴は、証明生成時間と証明サイズにおいて、ハッシュチェーンとスキップリストの両方を遙かに上回る。特に、個々のクライアントと監査者がコミットメントのサブセットのみを監査する場合、または部分証明が使用される場合にその傾向が顕著である。

正準表現 (canonical representation). ハッシュチェーン履歴と我々の履歴ツリーは、履歴と履歴内の証明の両方の正準表現を持つ。特に、与えられたコミットメント $C_n$ から各イベント $X_i$ への唯一の経路が存在する。経路が複数ある場合、単一の履歴内だけでなくロガーによってコミットされた履歴ストリーム $C_i,C_{i+1},\ldots$ 間でも代替経路の整合性をチェックする必要があるため、監査はより複雑になる。追加の経路は、スキップリストなどで過去のイベントを検索する効率を改善したり、より多くの機能を提供したりする可能性があるが [17]、監査者によって信頼されることはできずチェックされなければならない。

Maniatis と Baker [43] は対数サイズの証明をサポートしていると主張しているが、この多重経路問題に悩まされている。内部一貫性を保証するために、ロガーと事前のコンタクトがない監査者は、すべての増分証明または所属証明でログ内のすべてのイベントを受信しなければならない。

ロガーと定期的にコンタクトし、部分証明を使用し、増分監査間で $O(\log_2 n)$ の状態をキャッシュする監査者の場合は、効率が改善する。監査者が事前に $C_j$ までのロガーの内部一貫性を検証している場合、監査者はイベント $X_{j+1} \ldots X_n$ の受信により、将来のコミットメント $C_n$ までのロガーの内部一貫性を検証できる。スキップリストが内部的に一貫していることを監査者が知ると、対数的検索を可能にするリンクが信頼でき、古いイベントの後続の所属証明は $O(\log_2 n)$ 時間で実行される。スキップリストの履歴はこのモードで機能するように設計されており、各監査者は最終的にログ内のすべてを受信する。

監査が必要. ハッシュチェーンとスキップリストは新しいイベントを追加するときのみ履歴ツリーに対して複雑さの利点を提供するが、この利点は一時的なものである。特定のコミットメントが監査されないことをロガーが知っていれば、そのコミットメントによって修正されたイベントを自由に改ざんすることができ、ログはもはや証明可能な改ざん証跡ではなくなる。ロガーによって返されるすべてのコミットメントは監査される可能性が非ゼロでなければならず、改ざん防止ログの評価にはこの避けられない監査のコストを含めなければならない。複数の監査者が居る場合、監査のオーバーヘッドはさらに増大する。イベント挿入後、ハッシュチェーンとスキップリストは、返されたコミットメントと以前のコミットメント間で増分監査を行う瞬間に $O(n-j)$ の不利益を被る。例えば、コミットメントのランダムなサブセットのみを監査するといった方法ではこのオーバーヘッドを削減することはできない。

脅威モデルが常に信頼できないロガー (always-untrusted logger) から前方整合性脅威モデル (セクション 2.4 参照) に弱められたとしても、ハッシュチェーンとスキップリストは履歴ツリーよりも効率が劣る。クライアントは追加されたばかりのイベントの監査を省略できるが、ハッシュチェーンやスキップリストでは高コストとなる以前のコミットメントへの増分監査を実行する必要がある。

4 Merkle 集約

我々の履歴ツリーは、インデックスが与えられた任意のイベントに $O(\log_2 n)$ でのアクセスを可能にする。このセクションでは、履歴ツリーを拡張し、効率的で改ざん証跡機能を備えたコンテンツ検索をサポートする。Merkle 集約 (Merkle aggregation) と呼ぶこの機能により履歴ツリーに補助情報をエンコードする。これにより、ロガーはログの認可された削除を実行できると同時に、許可されていない削除を検出できる。この機能は安全な削除 (safe deletion) と呼ぶ。

例えば、クライアントがログ内の特定のイベントを保存時に "重要" フラグを付けるとする。履歴ツリーでは、ロガーはこれらのフラグを内部ノードに伝播し、いずれかの子ノードにフラグが付けられるたびにフラグを設定する。タグ付けされた履歴が改ざん証跡機能を備えていることを保証するために、このフラグをノードのハッシュラベルに組み込み、監査時にチェックすることができる。クライアントはログに挿入する際に信頼されていると想定されるため、我々はクライアントがイベントに適切な注釈を付けるものと想定する。所属監査は、ロガーが誤ったフラグを持つリーフを誤って保存した場合や、フラグを不適切に伝播した場合に検出する。増分監査は、凍結されたノードのフラグが変更された場合に改ざんを検出する。監査者がフラグ付きイベントのみのリストを要求した場合、ロガーはそのリストと、リストが完全であることの証明を生成できる。"重要" イベントが比較的少ない場合、クエリー結果は履歴の大部分をスキップできる。

フラグ付きイベントのリストが完全であることの証明を生成するために、ロガーは履歴ツリー $H$ 全体を走査し、フラグが設定されていない部分木を剪定し、訪問したノードのみを含む剪定ツリー $P$ を返す。監査者は、$P$ に対して独自の再帰走査を実行し、すべてのスタブがフラグなしであることを確認することで、$P$ においてフラグ付きノードが省略されていないことを確認できる。

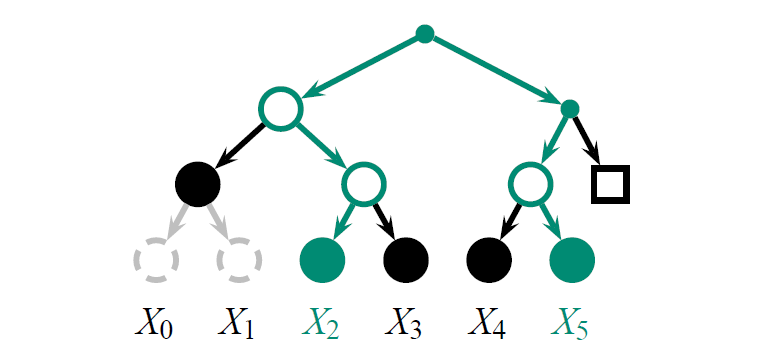
Figure 7 はイベント $X_2$ と $X_5$ がフラグ付きであるバージョン 5 の履歴に対するクエリーの剪定ツリーを示している。$X_2$ と $X_5$ からルートへの経路にある内部ノードもフラグ付きになる。$X_0$ と $X_1$ の親のように、一致するイベントを含まない部分木の場合、その子がフラグなしであることを保証するために、部分木のルートのみを保持する必要がある。

Figure 7: 重要フラグが付けられた (ハイライトされた) いくつかのイベントによる Merkle 集約のデモ。クエリに含まれるであろう凍結ノードは黒い丸として表現されている。

4.1 一般的な属性

ブール型のフラグは、後のクエリーのためにログイベントにフラグを付ける方法の一つに過ぎない。我々は考えられるすべての変種を列挙するのではなく、属性上の集約戦略を 3 タプル $(\tau,\oplus,\Gamma)$ に抽象化する。$\tau$ はイベントが持つ属性の型を表す。$\oplus$ は、ノードの子の属性を集約することによって履歴ツリーの内部ノードの属性を計算するために用いられる決定論的関数である。$\Gamma$ はイベントをその属性にマッピングする決定論的関数である。クライアントフラグ付きイベントの例では、集約戦略は $(\tau := {\rm BOOL},$ $\oplus:=\lor,$ $\Gamma(x):=x.isFlagged)$ となる。

例えば銀行アプリケーションでは、属性は取引のドル値であり、MAX 関数で集約され、特定のドル値を超えるすべての取引を見つけ、ロガーが結果を改ざんするかどうかを検出するクエリーを可能にする。これは $(\tau:={\rm INT},\oplus:={\rm MAX},\Gamma(x):=x.value)$ に相当する。あるいはクライアントによって胃生成された内部スタンプを持つイベントが、ロガーに順番通りに到着しない場合を考えてみよう。ツリー内の各ノードに、その子の間で見つかった最も早いタイムスタンプと最も遅いタイムスタンプで属性を付ける場合、イベントの到着順序に関係なく、与えられた時間範囲のすべてのノードについてロガーにクエリーできるようになる。

Merkle 集約を用いてログ全体のキーワード検索を実装するには、少なくとも 3 つの方法がある。キーワード数が事前に固定されている場合、イベントの属性 $\tau$ はビットベクトルまたはスパースベクトルと $\oplus:=\lor$ の組み合わせにすることができる。キーワードの数が不明だが少数である可能性が高い場合、$\tau$ はソートされたキーワードリストにすることができ、$\oplus:=\cup$ (和集合) となる。キーワード数が不明で、無限になる可能性がある場合は $\tau$ をビットベクトルとし、$\oplus:=\land$ としたブルームフィルター [8] を使用してキーワードを表すことができる。もちろん、ブルームフィルターはクエリーに対して偽陽性を返す可能性があるが、偽陰性は発生しない。

Merkle 集約は、$\Gamma$ が任意の決定論的計算可能関数になり得るため極めて柔軟である。ただし、ログが作成されると $(\tau,\oplus,\Gamma)$ はそのログに対して固定され、実行可能なクエリーのセットは選択された集約戦略に基づいて制限される。セクション 5 では、これらの概念を Syslog ログで使用されるメタデータにどのように適用できるかについて説明する。

4.2 形式的記述

履歴ツリーにおいて属性の改ざん証跡をおこなうために、我々はツリー状のハッシュ計算を修正してそれらを含める。各ノードは $A_{i,r}^v.H$ で表されるハッシュラベルと、属性を保存するための$V_{i,r}^v.A$ で表される注釈を持つ。これらを合わせて履歴ツリーの各ノードに付与されるノードデータを構成する。ノードのハッシュラベル $A_{i,r}^v.H$ には自身の属性 $A_{i,r}^v.A$ を固定しないことに注意。代わりに我々は部分木認証子 (subtree authenticator) $A_{i,r}^v.* = H(A_{i,r}^v.H\,||\,A_{i,r}^v.A)$ を定義し、これによってノードの属性とハッシュを確定し、その部分木内のすべてのハッシュと属性を再帰的に確定する。凍結ハッシュの ${\rm FH}_{i,r}.A$ と ${\rm FH}_{i,r}.H$、${\rm FH}_{i,r}.*$ は Merkle 集約を用いない場合と同様に定義される。

この再帰はいくつかの方法で定義できる。この表現により、1 つのハッシュと 1 組の属性を含む小さなスタブを用いて部分木を省略し、属性が適切に集約されているかどうかをローカルで検出できるような方法で属性を公開することができる。

ノードのハッシュと集約を計算するための新しいメカニズムは Figure 8 の式 ($\ref{eq5}$)-($\ref{eq10}$) で与えられる。この再帰式と Figure 5 に示した以前の再帰との間には強い対応がある。式 ($\ref{eq6}$) と ($\ref{eq7}$) は、式 ($\ref{eq1}$) と同様にイベントのハッシュと属性を抽出する。式 ($\ref{eq9}$) はノードのその子ノード間の属性の集約を扱う。式 ($\ref{eq8}$) はノードのハッシュをその子ノードの部分木認証子を用いて計算する。

${\rm Incr.Gen}$ と ${\rm Membership.Gen}$ は通常の履歴ツリーと同じように動作するが、証明 (${\rm FH}_{i,r}$) に凍結ハッシュが含まれていた箇所ではノードのハッシュ ${\rm FH}_{i,r}.H$ とその属性 ${\rm FH}_{i,r}.A$ の両方が含まれるようになる。これらは両方とも親ノードの $A_{i,r}^v.A$ と $A_{i,r}^v.H$ を再計算するために必要である。${\rm Add}$, ${\rm Incr.Vf}$, ${\rm Membership.Vf}$ は、ハッシュの計算と属性の伝播に ($\ref{eq5}$)-($\ref{eq10}$) を用いる点を除いて以前と同じである。Merkle 集約はストレージと証明のサイズを $(A+B)/A$ 倍にする。ここで $A$ はハッシュのサイズ、$B$ は属性のサイズである。

\[ \begin{eqnarray} A_{i,r}^v.* & = & H(A_{i,r}^v.H \, || \, A_{i,r}^v.A) \label{eq5} \\ A_{i,0}^v.H & = & \left\{ H(0 \, || \, X_i) \right. \quad \text{if $v \ge i$} \label{eq6} \\ A_{i,0}^v.A & = & \left\{ \Gamma(X_i) \right. \quad \text{if $v \ge i$} \label{eq7} \\ A_{i,r}^v.H & = & \left\{ \begin{array}{ll} H(1 \, || \, A_{i,r-1}^v.* \, || \, \square) \quad & \text{if $v \lt i+2^{r-1}$} \\ H(1 \, || \, A_{i,r-1}^v.* \, || \, A_{i+2^{r-1},r-1}^v.*) \quad & \text{if $v \ge i+2^{r-1}$} \\ \end{array} \right. \label{eq8} \\ A_{i,r}^v.A & = & \left\{ \begin{array}{ll} A_{i,r-1}^v.A \quad & \text{if $v \lt i+2^{r-1}$} \\ A_{i,r-1}^v.A \oplus A_{i+2^{r-1},r-1}-v.A \quad & \text{if $v \ge i+2^{r-1}$} \\ \end{array} \right. \label{eq9} \\ C_n & = & A_{0,d}^n.* \label{eq10} \end{eqnarray} \]

Figure 8: Merkle 集約におけるハッシュ計算

4.2.1 属性に関するクエリー

Merkle 集約クエリーでは、クエリー結果に偽陽性、つまりクエリー $\mathcal{Q}$ に一致しないイベントが含まれることを許容する。結果に含まれる偽陽性イベントは、監査によってフィルタリングできるため、パフォーマンスのみに影響して正確性には影響しない。偽陰性は禁止されており、$\mathcal{Q}$ に一致するすべてのイベントが結果に含まれる。

残念ながら、Merkle 集約クエリーは属性のみに一致でき、イベントは一致できない。結果として、我々はイベント上のクエリー $\mathcal{Q}$ を属性に関する述語 $\mathcal{Q}^\Gamma$ に保守的に変換し、それが以下の特性を持つ安定 (stable) であることを要求する: $\mathcal{Q}$ がイベントに一致する場合、$\mathcal{Q}^\Gamma$ はそのイベントの属性に一致する (すなわち $\forall_x \mathcal{Q}(x)$ $\Rightarrow$ $\mathcal{Q}^\Gamma(\Gamma(x))$)。さらに、あるノードのいずれかの子に対して $\mathcal{Q}^\Gamma$ が真である場合、そのノード自身に対しても $\mathcal{Q}^\Gamma$ が真でなければならない (すなわち $\forall_{x,y} \mathcal{Q}^\Gamma(x) \lor \mathcal{Q}^\Gamma(y)$ $\Rightarrow$ $\mathcal{Q}^\Gamma(x\oplus y)$ かつ $\forall_x \mathcal{Q}^\Gamma(x) \lor \mathcal{Q}^\Gamma(\square)$ $\Rightarrow$ $\mathcal{Q}^\Gamma(x \oplus \square)$)

安定した述語は 2 つの理由によりノードまたはイベントと誤って一致する可能性がある。これは、イベントが $\mathcal{Q}$ に一致しないにもかかわらずイベントの属性が $\mathcal{Q}^\Gamma$ に一致する場合、または、$(\mathcal{Q}^\Gamma(x) \lor \mathcal{Q}^\Gamma(y))$ が偽であるにもかかわらず $\mathcal{Q}^\Gamma(\Gamma(x))$ が真となるノードが出現する場合である。誤った一致が全く存在しない場合、述語 $\mathcal{Q}$ は正確 (exact) である。これは $\mathcal{Q}(x)$ $\Leftrightarrow$ $\mathcal{Q}^\Gamma(\Gamma(x))$ かつ $\mathcal{Q}^\Gamma(x) \lor \mathcal{Q}^\Gamma(y)$ $\Leftrightarrow$ $\mathcal{Q}^\Gamma(x\oplus y)$ の場合に当てはまる。正確なクエリーは、誤って一致したイベントがクエリー結果に含まれず、クエリー結果の正しさを証明する対応する剪定ツリーに追加のノードを必要としてないため、より効率的である。

これらの特性を用いて述語 $\mathcal{Q}^\Gamma$ に一致するイベントについてログに対して認証クエリーを実行するための追加操作を定義できる。

$H.{\rm Query}(C_j,\mathcal{Q}^\Gamma) \to P$. 属性 $\tau$ に対する述語 $\mathcal{Q}^\Gamma$ が与えられた場合、省略されたすべての部分木が $\mathcal{Q}^\Gamma$ に一致しない剪定ツリーを返す。
$P.{\rm Query.Vf}(C''_j,\mathcal{Q}^\Gamma) \to \{\top,\bot\}$. 剪定ツリー $P$ をチェックし、$P$ 内のすべてのスタブが $\mathcal{Q}^\Gamma$ に一致せず、再構築されたコミットメント $C_j$ が $C'_j$ と同じ場合に $\top$ を返す。

述語 $\mathcal{Q}^\Gamma$ に一致するすべてのイベントを含む剪定ツリーの構築は、所属監査または増分監査用の剪定ツリーの構築に似ている。ロガーは証明スケルトンから開始し、それを再帰的に走査し、$\mathcal{Q}^\Gamma({\rm FH}_{i,r}.A)$ が真である場合に内部ノードを分割する。述語 $\mathcal{Q}^\Gamma$ は安定であるため、省略された部分木内のどのイベントも述語に一致しない。述語 $\mathcal{Q}^\Gamma$ に一致するイベントが $t$ 個ある場合、剪定ツリーのサイズは最大で $O((1+t)\log_2 n)$ となる (つまりルートへの経路上に $\log_2 n$ 個の内部ツリーノードを持つ葉が $t$ 個ある)。

$P$ が $\mathcal{Q}^\Gamma$ に一致するすべてのイベントを含んでいることを検証するために、監査者は $P$ を再帰的に走査する。監査者が $\mathcal{Q}^\Gamma({\rm FH}_{i,r}.A)$ が真となる内部スタブを発見した場合、分割されるはずだったノードを発見したことになるため検証は失敗する。(非凍結ノードは証明スケルトンを構築するために常に分割され、$X_j$ からルートへの経路上にのみ出現する。) 監査者は、式 ($\ref{eq5}$)-($\ref{eq10}$) を使用してルートコミットメント $C_j$ を再構築し、$C_j = C'_j$ であることを確認することによって、剪定ツリー $P$ がコミットメント $C'_j$ と同じイベントをコミットしていることも検証する必要がある。

通常の履歴ツリーと同様に、Merkle 集約ツリーは改ざん検出のために監査を必要とする。イベントが一度も監査されていない場合、その属性が適切に含まれているという保証はない。また、不正なロガーやクライアントがツリーのルートまで属性が集約された偽のログエントリを意図的に挿入し、クエリーに不要な結果が含まれるようにすることもできる。しかし $\mathcal{Q}$ が安定であれば、悪意のあるロガーは一致するイベントを検出されることなくクエリー結果から隠蔽することはできない。

4.3 アプリケーション

安全な削除. Merkle 集約は、ある術簿を満たさない古いイベントや廃止されたイベントを期限切れにし、他のイベントが不適切に削除されていないことを証明するために使用できる。Merkle 集約クエリーは、一致するイベントがクエリー結果から除外されていないことを証明するが、安全な削除には逆証明 (contrapositive) が必要である。つまり、監査者に対して削除された各イベントが述語に一致しなかったため正当に削除されたことを証明する必要がある。

ロガーが保持する必要のあるすべてのイベントに対して真となる安定したクエリーを $\mathcal{Q}(x)$ とする。$\mathcal{Q}^\Gamma(x)$ を属性に対する対応する述語とする。ロガーは、$\mathcal{Q}^\Gamma(x)$ が真となるすべてのノードと葉イベントを含む剪定ツリーを保存する。残りのノードは省略されてスタブに置き換えられる場合がある。ロガーが以前に削除されたイベント $X_i$ への経路を生成できない場合、代わりに $\mathcal{Q}^\Gamma(A)$ が偽となる $X_i$ の祖先ノード $A$ への経路を含む剪定ツリーを提供する。$\mathcal{Q}$ は安定であるため、$\mathcal{Q}^\Gamma(A)$ が偽であれば $\mathcal{Q}^\Gamma(\Gamma(X_i))$ も $\mathcal{Q}(X_i)$ も偽でなければならない。

安全な削除と監査ポリシーは、イベント $X_i \ldots X_j$ を含む部分木が削除された場合、ロガーはコミットメント $C_i \ldots C_j$ を含む増分証明または所属証明を生成できないことを考慮する必要がある。監査ポリシーでは、これらのコミットメントを使用する監査が対応するイベントが削除される前に実行されることを要求しなければならず、これはクライアントが定期的に、より新しい、または長期間有効なコミットメントに対する増分証明を要求することを要求するだけの単純な方法でも良い。

セクション 3.3 で説明した追記専用ストレージを使用する場合、安全な削除によってスペースは節約されない。しかしデータは木ポリシーでログ内のイベントのサブセットを破棄する必要がある場合、許可されていないログイベントが破棄されていないことを証明するために安全な削除を使用できる。

"プライベート" 検索. Merkle 集約はプライベート情報検索 [14] の弱い変種を可能にし、クライアントがイベントの特定の内容についてプライバシーを確保できるようにする。イベントの属性を集約するため、ロガーはイベント自体ではなく、イベントの属性 $\Gamma(X_i)$ のみを必要とする。集約が正しく行われたことを検証するためにもイベントの属性のみが必要である。クライアントがイベントを暗号化し、公開属性にデジタル署名すれば、監査者は集約が正しく行われたことを検証しながら、クライアントはロガーや他のクライアント、監査者からイベントのプライバシーを保護することができる。

ブルームフィルタは、大量のキーワードの存在または不在を簡潔かつ近似的に表現する方法を提供するだけでなく、プライベートインデックス作成も可能にする (例えば Goh [23] 参照)。ロガーはブルームフィルター内の個々のキーワードが何であるかを知らない。多くのキーワードが同じビットマップにマッピングされる可能性がある。これにより、ツリーの整合性メカニズムによって保護されたプライベートキーワードが可能になる。

5 Syslog プロトタイプ実装

Syslog は標準的な Unix ベースのログシステム [38] であり、多くの属性を持つイベントを保存する。本論文で提案する履歴ツリーの有効性を示すために、我々は Systelog イベントを保存し検索できる実装を構築した。各部門サーバから取得した Syslog トレースのイベントを用いて改ざん防止ログと安全な削除のストレージコストと性能コストを評価した。

各 Syslog イベントは、タイムスタンプ、イベントを性生成したホスト、イベントを生成した 24 のファシリティまたはサブシステムのいずれか、8 つのログレベルのいずれか、そしてメッセージが含まれる。ほとんどのイベントには、イベントを生成したプログラムを示すタグも含まれている。ネットワークを介した Syslog イベントの認証、管理、および信頼性の高い配信のためのソリューションは既に提案されており [48]、標準化の過程にある [32] が、これらの研究はいずれも本論文で提供しようとしているログセマンティクスには対応していない。

我々のプロトタイプ実装は Python 2.5.2 と C++ のハイブリッドで記述され、4GB の RAM を搭載した Intel Core 2 Duo 2.4GHz CPU (Linux, 64 ビットモード) でベンチマークテストを実施した。我々の現在の実装はシングルスレッドであるため、2 つ目の CPU コアは十分に活用されていない。実装では OpenSSL ライブラリから借用した SHA-1 ハッシュと 1024 ビット DSA 署名を使用している。

我々の実装ではセクション 3.3 で議論された配列ベースの後順走査表現を使用する。値ストアと履歴ツリーは別々の追記専用ファイルに保存され、メモリにマッピングされる。履歴ツリー内のノードは固定バイト数を使用するため直接アクセスが可能である。所属証明と増分証明の生成には証明のサイズ (ログ内のイベント数の対数) に比例した RAM が必要である。Merkle 集約クエリーの結果サイズは現在 RAM に収まるサイズ (約 400 万イベント) に制限されている。

我々の改ざん証跡履歴ツリーのストレージオーバーヘッドはわずかである。プロトタイプでは各イベントにつき 5 つの属性を格納する。タグとホスト名は 32 ビット中 2 ビットのブルームフィルターとして符号化される。ファシリティとホストはビットベクトルとして符号化される。特定の時間範囲内のすべてのイベントを見つける範囲クエリーを可能にするため、メッセージのタイムスタンプは間隔で符号化される。履歴ツリーの各ノードは合計 20 バイトの属性と 20 バイトの SHA-1 ハッシュを持つ。葉には値すと穴井のイベント内容のオフセットと長さを保存するために追加の 12 バイトを持つ。

我々は履歴ツリーの処理時間と空間オーバーヘッドを調べるためプロトタイプのシミュレーションを複数回実行した。この目的のため、我々は 13 の部門サーバホストから 106 時間かけて 400 万件のイベントとレースを収集した。9 つのファシリティ、6 つのレベル、および 32 の異なるタグを観察した。イベントの 88.1% メールサーバからのもので、11.5% は 98,743 件の失敗した SSH 接続によるものである。ログ行のわずか 0.393% がその他のソースからのものである。履歴ツリーのテストではこのトレースを 20 回再生して 8,000 万件のイベントを挿入した。再生後の Syslog トレースは 14.0GB を占有し、履歴ツリーはさらに 13.6GB を加える。

5.1 ロガーの性能

ロガーはこの設計における唯一の集中ホストであるためボトルネックとなる可能性がある。実際のロガーのパフォーマンスは監査ポリシーとイベントの挿入と監査要求の相対的な頻度に依存する。特定の監査ポリシーについてロガーの性能を要約するのではなく、ロガーが実行する様々なタスクのコストをベンチマークする。

取得した Syslog トレースの平均イベント数は 1 秒あたりわずか 10 件であった。プロトタイプは DSA 署名生成を含め 1 秒あたり 1,750 イベントの速度でイベントを挿入できる。イベントの挿入には Table 2 に示す 4 つのステップが必要とし、最終ステップとなる、結果として得られるコミットメントへの署名が処理時間の大部分を占める。DSA 署名を別の場所で計算する場合 (例えば複数の CPU コアを活用する場合)、スループットは 1 秒あたり 10,500 イベントまで向上する。(スケーラビリティについてはセクション 6 で詳しく説明する。) これは非圧縮の Syslog データで 1.9MB/秒 (一週間で 1.1TB) に相当する。

Table 2: イベントを挿入し、その結果のコミットメントに署名するときに必要な 4 つのステップにおけるロガーの性能、および所属証明を生成する際の性能。レートは、指定されたステップ以外の処理が行われていないことを前提に示されている。
ステップ	タスク	CPU %	レート (イベント/秒)
A	Syslog メッセージの解析	2.4%	81,000
B	ログにイベントを挿入	2.6%	66,000
C	コミットメントの生成	11.8%	15,000
D	コミットメントへの署名	83.3%	2,100
	所属署名 (局所性あり)	-	8,600
	所属署名 (局所性なし)	-	32

我々はプロトタイプが所属証明と増分証明を生成する速度も測定した。2 つのコミットメント間の増分証明のサイズは 2 つのコミットメント間の距離に依存する。距離は約 2 イベントから 200 万イベントまで変化するため、自己完結型証明のサイズは 1,200 バイトから 2,500 バイトまで変化する。これらの証明を生成する速度は 10,500 件/秒から 18,000 件/秒まで変換し、距離が短い方が長いよりも証明が小さくなり高速な性能を持つ。増分証明と所属証明のどちらも gzip [18] で圧縮すると証明のサイズは半分になるが、証明を生成する速度も半分になる。

履歴ツリーに 8,000 万件のイベントを挿入した後、履歴ツリーと値ストアは 27GB を必要とし、これはテストマシンの RAM 幼少の数倍に相当する。Table 2 は 2 つの所属監査シナリオの結果を示している。最初のシナリオでは、挿入された最新の 500 万件のイベントからランダムに選択したイベントの所属証明を要求した。プロトタイプは 1 秒あたり 8,600 件の自己完結型所属証明を生成し、平均でそれぞれ 2,400 バイトのサイズであった。この高い局所性シナリオでは最新の 500 万件のイベントが既に RAM に格納されていた。2 つ目のシナリオでは、ログ内の任意の場所にあるランダムなイベントの所属証明を要求することで、監査リクエストの局所性が低い状況を検証した。ロガーのパフォーマンスはディスクのシークレイテンシに制限された。証明サイズは平均 3,100 バイトで、性能は 1 秒あたり 32 回の所属証明に低下した。(この問題の解決方法についてはセクション 6.2 で説明する。)

履歴ツリーのスケーラビリティをテストするために、我々は複製なしの元の 400 万イベントの Syslog イベントトレースと、20 倍の複製後の 8000 万イベントトレースで、挿入パフォーマンスと監査性能をベンチマークした。イベントの挿入と増分監査はより大きいログで約 10% 遅くなる。

5.2 監査者とクライアントの性能

履歴ツリーは監査者やクライアントにはほとんど負担をかけない。監査者とクライアントは、ロガーのコミットメント署名を検証し、監査リクエストに対する剪定ツリーの応答の正しさを検証する必要がある。我々のマシンは 1 秒あたり 1,900 個の DSA-1024 署名を検証できる。現在のツリーパーサーは Python で記述されておりかなり低速である。1 秒あたり 480 個の剪定ツリーしか解析できない。剪定ツリーの解析が完了すると、我々のマシンは 1 秒あたり 9,000 個の増分証明または所属証明を検証できる。現在、1 つの監査者はロガーが生成できる速度で証明を検証することはできないが、監査者は互いに独立して並列に動作できることは明らかなため、必要に応じて非常に高いスケーリングが可能である。

5.3 Merkle 集約結果

このサブセクションではクエリー結果の生成と安全な削除における Merkle 集約の利点について説明する。我々の実験では、大規模な剪定ツリーを生成する実装上の制限のため、Merkle 集約実験ではより小規模な 400 万件のイベントログを使用した。

我々は安全な削除の利点と Merkle 集約クエリーのオーバーヘッドを調査するために 86 の異なる述語を使用した。それぞれ 1 つのタグに一致する述語を 52、1 つのホストに一致する述語を 13、1 つのファシリティに一致する述語を 9、各レベルに 1 つずつ一致する述語を 6、そして上位 $k$ 個のログレベルに一致する述語を 6 使用した。

タグとホストに一致する述語はブルームフィルターを使用しており、不正確 (inexact) であり偽陽性が発生する可能性がある。そのため、65 個のブルームフィルタークエリー結果のうちの 34 が、正確な述語に対する我々の "最悪ケース" の期待値よりも多くのノードを含む結果となった。より大きなブルームフィルターを使用することで誤った一致の可能性を軽減する。タグとホスト名に 64 ビット中 4 ビットのブルームフィルターを使用すると、検索クエリーから生成される剪定ツリーでは、履歴ツリーの各ノードに 64 ビットの属性が追加で必要になるが、ノード数は平均 15% 減少する。実際の実装では、ブルームフィルターの正確なパラメータはログに記録されるイベントのサンプルに合わせて調整するのが最適である。

Merkle 集約と安全な削除. 安全な削除によってログから不要なイベントを削除できる。監査者はイベントの属性に対して、保持すべきイベントを示す安定した述語を定義し、ロガーは一致するイベントのみを含む剪定ツリーを保持する。最初のテストでは、解く知恵のホストからのイベントを除くすべてのイベントを削除するシミュレーションを行った。剪定ツリーは 14 秒で生成され、ログ全体のイベントの 1.92% が含まれ、ツリー全体のサイズの 2.29% にシリアライズされた。98.08% のイベントが削除されたが、ロガーは省略された部分木のルートノードのハッシュラベルと属性を保持する必要があるため、履歴ツリー内のノードの 95.1% しか削除できなかった。

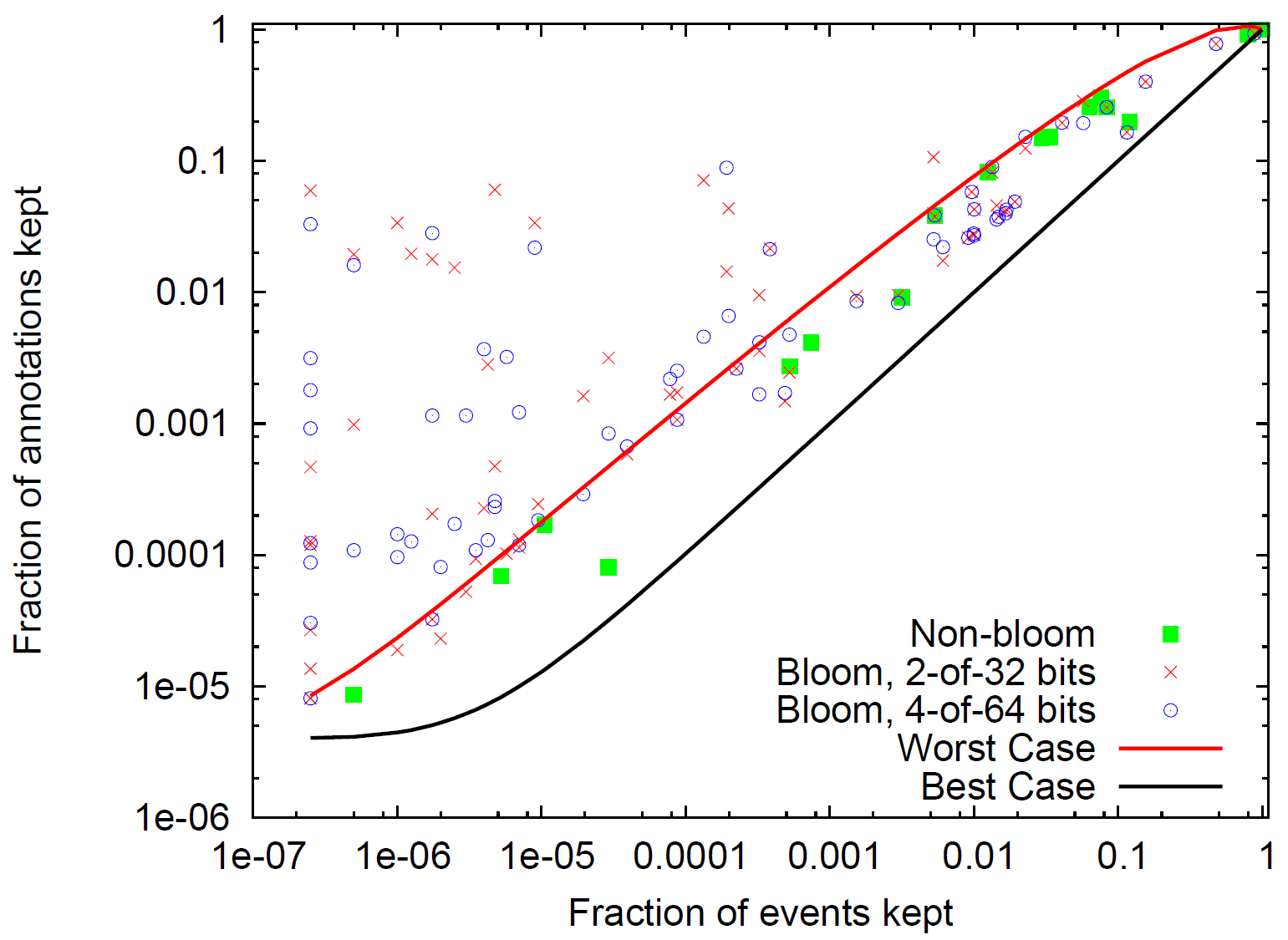
安全な削除によって生成された剪定履歴ツリーのサイズを測定する際、ロガーは証明を迅速に生成できるように、すべての内部ノードのハッシュと属性をキャッシュすると仮定する。各述語について保持比率 (kept ratio) を測定する。これは、述語に一致するすべてのノードの剪定ツリー内の内部ノードまたはスタブの数を完全な履歴ツリーの内部ノードの数で割った値である。Figure 9 は、各述語について保持率と述語に一致するイベントの割合をプロットしている。また、連続近似に基づいて、解析的な裁量ケースと最悪ケースの境界もプロットしている。一致するイベントがログ内で連続している場合にオーバーヘッドが最小となる。最悪ケースはイベントガロ具内で最大限に離れているときに発生する。ブルームフィルタークエリーは "最悪ケース" の境界よりも性能が悪化する。これは、ブルームフィルターの一致が不正確であるため、内部ノードで偽陽性一致が発生し、結果として得られる剪定ツリーにそれらのノードが残ってしまうためである。多くのブルームフィルターは "最悪ケース" よりもはるかに悪い性能を示したが、ログ内のイベントの 1% 未満にしか一致しなかったブルームフィルターでは、ロガーは履歴ツリーのノードの 90% 以上を削除することができ、多くの場合、それよりもはるかに良い結果を示した。

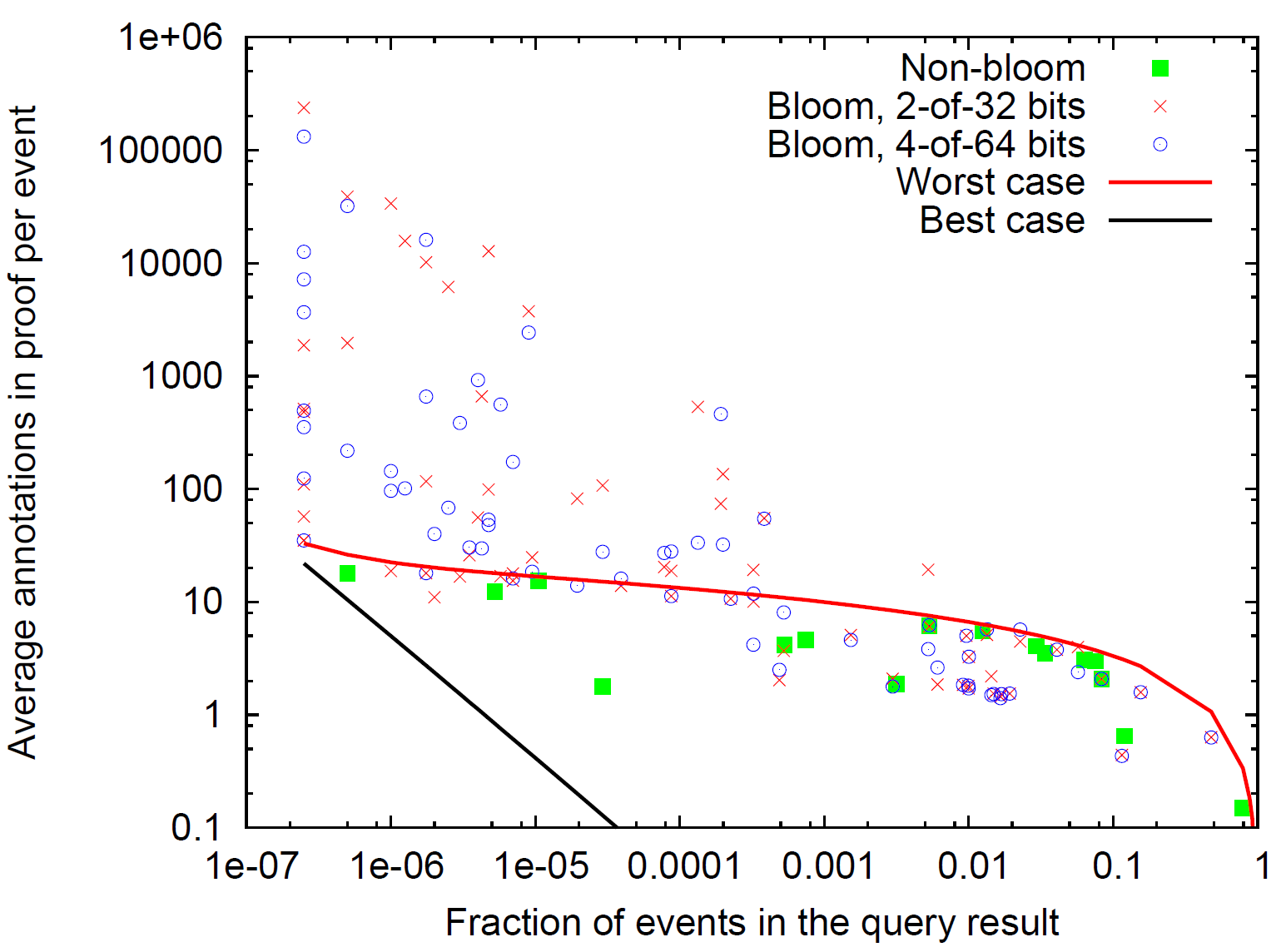
Figure 9: 安全な削除オーバーヘッド。様々なクエリについて、削除後も保持されるハッシュと属性の割合と保持されるイベントの割合をプロットしている。

Merkle 集約と認証済みクエリー結果. 我々の第 2 のテストでは Merkle 集約クエリーの検索結果のオーバーヘッドを調査する。ロガーがクエリーの結果を生成すると、結果として得られる剪定ツリーには一致したイベントトイレ器ツリーのオーバーヘッドの両方が、スタブのハッシュと属性の形式で含まれる。各述語について、我々はクエリーオーバーヘッド比率を測定する。これは、剪定ツリー内のスタブと内部ノードの数を剪定ツリー内のイベント数で割ったものである。Figure 10 では我々の 86 の述語それぞれについてクエリーオーバーヘッド比率とクエリーに一致するイベントの割合をプロットしている。このプロットは述語に一致する各イベントについて、認証情報のために 1 イベントあたりどれだけの追加オーバーヘッドが発生しているかを比例的に示している。我々はまた連続近似に基づく解析的な裁量ケースと最悪ケースの境界もプロットする。最小オーバーヘッドは一致するイベントがログ内で連続している場合である。

Figure 10: イベントあたりのクエリーオーバーヘッド。各クエリの結果におけるハッシュとマッチするイベントの数と、クエリにマッチするイベントの割合の比率をプロットしている。

6 改ざん証跡ログのスケーリング

このセクションでは並行性を利用して履歴ツリーへの挿入スループットを向上させる手法と、複製によって監査スループットを改善する手法について説明する。また、複数のイベントに渡ってデジタル署名のオーバーヘッドを償却する手法についても説明する。

6.1 並行性による挿入の高速化

我々の改ざん証跡ログは並行性を活用してスループットを向上させる多くの機会を提供する。おそらく最もシンプルなアプローチは署名生成をオフロードすることである。Table 2 では署名の挿入は実行時コストの 80% 以上を占めている。署名は他のハッシュには含まれず、署名計算の間に相互依存性はない。さらに、コミットメントへの署名には履歴ツリーのルートコミットメント以外の情報は必要ない。したがって、署名計算を追加の CPU コア、追加のホスト、またはハードウェア暗号化アクセラレータにオフロードすることでスループットを改善させることは容易である。

ロガーがコミットメントを並行して生成することも可能である。Table 2 を見ると、ログへのイベントの解析と挿入はコミットメントの生成よりも約 2 倍高速であることが分かる。署名と同様にコミットメントも相互依存性がなく署名ツリーの内容のみに依存する。イベント $X_j$ がツリーに挿入され、$O(1)$ の凍結ハッシュが計算・保存されるとすぐに、新しいイベントを直ちにログに記録できるようになる。コミットメント $C_j$ の計算には履歴ツリーへの読み取り専用アクセスのみが必要であるため、後続のイベントに干渉することなく別の CPU コアで同時に計算できる。共有メモリを使用して履歴ツリーの追記専用かつ一度しか書き込みできないセマンティクスを利用することで並行性のオーバーヘッドは低くなると予想される。

我々は、セクション 5 で説明したプロトタイプ実装において、汎用ハードウェア上の CPU コア 1 個のみを使用して毎秒 38,000 イベントの Syslog イベントをログに挿入できる最大速度を実験的に検証した。これはハードウェアが潜在的にサポートできる最大スループットである。このモードでは、デジタル署名、コミットメント生成、監査リクエストは追加の CPU コアまたはホストに委譲されることを想定している。ホストが複数ある場合、各ホストは履歴ツリーのレプリカを構築する必要があるが、これは少なくとも最大挿入速度である毎秒 38,000 イベントと同等の速度で実行できる。これらのホスト上の追加の CPU コアはコミットメント生成や監査リクエストの処理に使用できる。

アプリケーションによっては毎秒 38,000 イベントでも依然として十分に高速ではない可能性がある。これを超えてスケールするには、イベント挿入および保存タスクを複数のログに分割する必要がある。これらの間の相互依存性を断つため、我々が現在使用している基本的な履歴ツリーのデータ構造を進化させる必要がある。おそらくタイムラインエンタングルメント [43] のように、時折互いに絡み合う分離ログに発展する必要があるだろう。このような構造の設計と評価は今後の課題である。

6.2 RAM より大きいログ

ワーキングセットのサイズが RAM に収まらないような非常に大規模な監査またはクエリーの場合、スループットはディスクシークのレイテンシに制限されることが観測された。同様の問題は二次記憶装置を使用するあらゆるデータベースクエリーシステムで発生する。データベースでクエリーを高速化する他面使用されているものと同じソフトウェアおよびハードウェア技術、例えば、より高速または高スループットのストレージシステムや、データを分割して複数のマシンのクラスタにまたがるメモリ内に格納する手法などが利用できる。そして、各部分木を管理するクラスタノードに単一の大きなクエリーを発行することができる。そして、その結果は監査装置に送信される前にマージされる。各部分木はホストの RAM に収まるため、サブクエリーは高速に実行される。

6.3 イベントのバッチ署名

大規模なコンピュータクラスタが利用できず、DSA 署名の性能コストがロガーのスループットの制限要因となる場合、複数の更新を 1 回の署名計算で処理できるようにすることでロガーの性能を向上させることができる。

通常、クライアントがイベント $X$ の挿入をリクエストすると、ロガーはイベント $X$ にインデックス $i$ を割り当てコミットメント $C_i$ を生成し署名して結果を返す。ロガーの CPU 能力がすべてのコミットメントに署名するのに十分でない場合、ロガーは代わりに後のコミットメント $C_j$ ($j \ge i$) の署名が得られるまで $C_i$ の返信を送らせることができる。この署名済みコミットメントはより速いコミットを期待するクライアントに送信できる。$C_j$ によってコミットされたログ内のイベント $X_i$ が $X$ であることを保証するために、クライアントはコミットメント $C_j$ からイベント $i$ への所属証明を要求し、$X_i = X$ であることを検証することができる。これは我々の構造の改ざん証跡によって安全である。後になってロガーが $C_j$ と矛盾する $C_i$ に署名した場合、増分証明は失敗する。

我々のプロトタイプでは、ログへのイベント挿入はコミットメントの生成と署名より 20 倍高速である。ロガーは、署名付きコミットメントの生成コストを多数の挿入イベントに分散させることができる。署名付きコミットメントあたりのイベント数はロガーの負荷に応じて動的に変化する可能性がある。負荷が軽い場合、ロガーはすべてのコミットメントに署名し 1 秒あたり 1,750 イベントを挿入できる。負荷が増加すると、ロガーは 16 のコミットメントごとに 1 つ署名し、推定挿入速度は 1 秒あたり 17,000 イベントになる可能性がある。クライアントは依然として数分の 1 秒以内に署名付きコミットメントを受け取るが、複数のクライアントが同じコミットメントを受け取ることができるようになる。この分析では、ログの最大挿入速度のみを考慮しており、監査への返信にかかるコストは含まれていないことに注意。全体的なパフォーマンス向上はクライアントが増分証明と所属証明を要求する頻度に依存する。

近年、規制村主のための追記型データベースの作成に関心が集まっている。これらのデータベースは古いバージョンへのアクセスと改ざんの追跡を可能にする [51]。B-Tree [64] や全文インデックス [47] などの様々なデータ構造が用いられている。これらのシステムのセキュリティは基盤となるストレージの write-once 背マンディクスに依存しており、このセマンティクスはリモート監査者が独立して検証することはできない。

Forward-Secure デジタル署名方式 [3] やストリーム認証 [21] は我々の方式や他のログ記録方式におけるコミットメントの署名に使用できる。ログ内のエントリはプライバシー保護のためクライアントによって暗号化される可能性がある。Kelsey と Schneier [57] は、エントリを暗号化し使用後に破棄される鍵をロガーが使用することで、攻撃者が過去のログエントリを読み取ることを防止している。これはハッシュ関数を反復処理することで暗号化鍵を生成する。最初のハッシュは信頼できる監査者に送られ、イベントを復号化する。Logcrypt [29] はこれを公開鍵暗号に拡張している。

Ma と Tsudik [41] は Forward-Secure 逐次集約署名方式 [39, 40] を用いて構築された改ざん証跡ログを検討している。彼らの設計はラウンドベースである。各ラウンドにおいて、ロガーは署名を進化させ新しいイベントを既存の署名と組み合わせて新しい署名を生成するとともに、認証鍵も進化させる。ラウンドの終了時に最終的な署名は挿入された任意のイベントを認証できる。

Davis ら [17] はロガーが各キーワードに対して並列ハッシュチェーンを構築することを信頼することでログ内のキーワード検索を可能にしている。暗号化されたログをキーワード検索するための技術も設計されている [60, 61]。追記専用署名に基づく投票機向けの改ざん証跡ストアが提案されている [33] が、署名サイズ葉署名されたメッセージ数と共に増加する [6]。

文献では多くのタイムスタンプサービスが提案されている。Haber と Stornetta [27] はハッシュチェーンに基づくタイムスタンプサービスを導入し、これが週に一度新聞でヘッドコミットメントを掲載する商用タイムスタンプサービスである Surety の設計に影響を与えた。Chronos はスキップリストに着想を得たデジタルタイムスタンプサービスだが、ハッシュ構造は我々の履歴ツリー [7] に似ている。このサービスや他のタイムスタンプ設計 [9, 10] はラウンドベースである。各ラウンドにおてい、ロガーはイベントセットを収集しそのラウンド内のイベントをツリー、スキップリスト、または DAG に格納する。ラウンドの終了時、ロガーはそのラウンドのコミットメントを公開ブロードキャストする (例えば新聞で)。クライアントは、イベントがそのラウンド内に保存され、公開されたコミットメントと一致していることを示す対数サイズの改ざん証跡証明を取得する。ラウンド内の連続するイベントのタイムスタンプ認証情報をストリーミング形式で出力するための効率的なアルゴリズムが構築されており、サーバ上のストレージ容量は最小限に抑えられている [37]。これらのシステムとは異なり、我々の履歴ツリーではイベント路を津に追加し、コミットメントを生成し、いつでも監査を実行できる。

Maniatis と Baker [43] はタイムラインエンタングル (timeline entanglement) という概念を導入した。これは分散システムのすべての参加者がログを保持するというものである。メッセージを受信するたびにログに追加され、送信されるすべてのメッセージにはログヘッドのハッシュが含まれる。このプロセスによりコミットメントがネットワーク全体に拡散され、悪意のあるノードが正規のタイムラインから逸脱することが困難になる。その証拠は監査で改ざんを検出するための証拠として使用できる。Auditorium [55] はこの特性を利用して $N-1$ 個のシステムが故障しても改ざんを検出できる共有 "掲示板" を作成する。

セキュア集約は、集約を行うホストが信頼できない場合に、合計、中央値、その他集約値を計算するためのセンサーネットワークにおける分散プロトコルとして研究されてきた。手法としては、近似結果を犠牲にして通信複雑度を線形以下に抑える [12]、あるいは MAC コードを用いて集約計算に置ける椀ホップエラーを検出する [30] などが挙げられる。他の集約プロトコルは、我々が Merkle 集約のために開発したハッシュツリー構造に類似した構造に基づいている。これらの構造は集約と暗号学的ハッシュを組み合わせたもので、認証付き合計を計算するための分散センサーネットワーク集約プロトコル [13] や汎用集約 [45] などが含まれる。センサーネットワーク集約プロトコルは一連の測定値の安全な集約を対話的に生成する。Merkle 集約では中間集約を効率的なクエリーを実行するためのツールとして用いる。また、我々の Merkle 集約の構築はこれらの設計よりも効率的であり、イベントの検証に必要な暗号学的ハッシュの数が少なくなる。

8 結論

本研究において、我々は滴々かつ継続的な監査があらゆる改ざん証跡ログシステムにとって極めて重要な操作であることを示した。監査がなければ、クライアントはビザンチンロガーがイベントを記録しなかったり、監査されていないイベントを削除したり、ログをフォークしたりするなど、不正な動作をしている場合を検出できない。この要件に基づき、ロガーが正しい動作の簡潔な証明を生成できるようにする新しい Merkle ツリーデータ構造に基づく改ざん証跡ログの新しい設計を開発した。このシステムはロガーを信頼する必要をなくし、代わりにクライアントとロガーの監査者が一定量のローカル状態のみでロガーの正しい動作を効率的に検証できるようにする。クライアントと監査者の間でコミットメントを共有することで、クライアントが考えを変えて以前に記録したイベントを否認しようとした場合でも高度なフォーク攻撃やロールバック攻撃に対して耐性がある。

また Merkle 集約も提案した。これは補助属性を Merkle ツリーにエンコードする柔軟なメカニズムであり、これらの属性をツリーの葉からルートまで検証可能な方法で集約できる。この手法により、効率的で改ざん証跡機能を備えた幅広いクエリーを実行できるだけでなく "期限切れ" イベントをログから検証可能かつ安全に削除することも可能である。

プロトタイプ実装は 1 秒あたり数千件のイベントをサポートし、非常に大規模なログにも容易に拡張できる。また、ブルームフィルーターを用いることで幅広いクエリーに対応できることも実証した。この手法の簡潔な証明とスケーラブルな設計により、大量のログイベントによって改ざん証跡機能のログの使用が妨げられる可能性のある様々な分野に適用できる。

Acknowledgements

The authors gratefully acknowledge Farinaz Koushanfar, Daniel Sandler, and Moshe Vardi for many helpful comments and discussions on this project. The authors also thank the anonymous referees and Micah Sherr, our shepherd, for their assistance. This work was supported, in part, by NSF grants CNS-0524211and CNS-0509297.

References

ACCORSI, R., AND HOHL, A. Delegating secure logging in pervasive computing systems. In Security in Pervasive Computing (York, UK, Apr. 2006), pp. 58–72.
ANAGNOSTOPOULOS, A., GOODRICH, M. T., AND TAMASSIA, R. Persistent authenticated dictionaries and their applications. In International Conference on Information Security (ISC) (Seoul, Korea, Dec. 2001), pp. 379–393.
BELLARE, M., AND MINER, S. K. A forward-secure digital signature scheme. In CRYPTO '99 (Santa Barbara, CA, Aug. 1999), pp. 431–448.
BELLARE, M., AND YEE, B. S. Forward integrity for secure audit logs. Tech. rep., University of California at San Diego, Nov. 1997.
BENALOH, J., AND DE MARE, M. One-way accumulators: a decentralized alternative to digital signatures. In Workshop on the Theory and Application of Cryptographic Techniques on Advances in Cryptology (EuroCrypt '93) (Lofthus, Norway, May 1993), pp. 274–285.
BETHENCOURT, J., BONEH, D., AND WATERS, B. Cryptographic methods for storing ballots on a voting machine. In Network and Distributed System Security Symposium (NDSS) (San Diego, CA, Feb. 2007).
BLIBECH, K., AND GABILLON, A. CHRONOS: An authenticated dictionary based on skip lists for timestamping systems. In Workshop on Secure Web Services (Fairfax, VA, Nov. 2005), pp. 84–90.
BLOOM, B. H. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM 13, 7 (1970), 422–426.
BULDAS, A., LAUD, P., LIPMAA, H., AND WILLEMSON, J. Time-stamping with binary linking schemes. In CRYPTO '98 (Santa Barbara, CA, Aug. 1998), pp. 486–501.
BULDAS, A., LIPMAA, H., AND SCHOENMAKERS, B. Optimally efficient accountable time-stamping. In International Workshop on Practice and Theory in Public Key Cryptography (PKC) (Melbourne, Victoria, Australia, Jan. 2000), pp. 293–305.
CAMENISCH, J., AND LYSYANSKAYA, A. Dynamic accumulators and application to efficient revocation of anonymous credentials. In CRYPTO '02 (Santa Barbara, CA, Aug. 2002), pp. 61–76.
CHAN, H., PERRIG, A., PRZYDATEK, B., AND SONG, D. SIA: Secure information aggregation in sensor networks. Journal Computer Security 15, 1 (2007), 69–102.
CHAN, H., PERRIG, A., AND SONG, D. Secure hierarchical in-network aggregation in sensor networks. In ACM Conference on Computer and Communications Security (CCS '06) (Alexandria, VA, Oct. 2006), pp. 278–287.
CHOR, B., GOLDREICH, O., KUSHILEVITZ, E., AND SUDAN, M. Private information retrieval. In Annual Symposium on Foundations of Computer Science (Milwaukee, WI, Oct. 1995), pp. 41–50.
CHUN, B.-G., MANIATIS, P., SHENKER, S., AND KUBIATOWICZ, J. Attested append-only memory: Making adversaries stick to their word. In SOSP '07 (Stevenson, WA, Oct. 2007), pp. 189–204.
D. S. PARKER, J., POPEK, G. J., RUDISIN, G., STOUGHTON, A., WALKER, B. J., WALTON, E., CHOW, J. M., EDWARDS, D., KISER, S., AND KLINE, C. Detection of mutual inconsistency in distributed systems. IEEE Transactions on Software Engineering 9, 3 (1983), 240–247.
DAVIS, D., MONROSE, F., AND REITER, M. K. Time-scoped searching of encrypted audit logs. In Information and Communications Security Conference (Malaga, Spain, Oct. 2004), pp. 532–545.
DEUTSCH, P. Gzip file format specification version 4.3. RFC 1952, May 1996. http://www.ietf.org/rfc/rfc1952.txt.
DEVANBU, P., GERTZ, M., KWONG, A., MARTEL, C., NUCKOLLS, G., AND STUBBLEBINE, S. G. Flexible authentication of XML documents. Journal of Computer Security 12, 6 (2004), 841–864.
DEVANBU, P., GERTZ, M., MARTEL, C., AND STUBBLEBINE, S. G. Authentic data publication over the internet. Journal Computer Security 11, 3 (2003), 291–314.
GENNARO, R., AND ROHATGI, P. How to sign digital streams. In CRYPTO '97 (Santa Barbara, CA, Aug. 1997), pp. 180–197.
GERR, P. A., BABINEAU, B., AND GORDON, P. C. Compliance: The effect on information management and the storage industry. The Enterprise Storage Group, May 2003. http://searchstorage.techtarget.com/tip/0,289483,sid5_gci906152,00.html.
GOH, E.-J. Secure indexes. Cryptology ePrint Archive, Report 2003/216, 2003. http://eprint.iacr.org/2003/216/ See also http://eujingoh.com/papers/secureindex/.
GOODRICH, M., TAMASSIA, R., AND SCHWERIN, A. Implementation of an authenticated dictionary with skip lists and commutative hashing. In DARPA Information Survivability Conference & Exposition II (DISCEX II) (Anaheim, CA, June 2001), pp. 68–82.
GOODRICH, M. T., TAMASSIA, R., TRIANDOPOULOS, N., AND COHEN, R. F. Authenticated data structures for graph and geometric searching. In Topics in Cryptology, The Cryptographers' Track at the RSA Conference (CT-RSA) (San Francisco, CA, Apr. 2003), pp. 295–313.
GOYAL, V., PANDEY, O., SAHAI, A., AND WATERS, B. Attribute-based encryption for fine-grained access control of encrypted data. In ACM Conference on Computer and Communications Security (CCS '06) (Alexandria, Virginia, Oct. 2006), pp. 89–98.
HABER, S., AND STORNETTA, W. S. How to time-stamp a digital document. In CRYPTO '98 (Santa Barbara, CA, 1990), pp. 437–455.
HAEBERLEN, A., KOUZNETSOV, P., AND DRUSCHEL, P. PeerReview: Practical accountability for distributed systems. In SOSP '07 (Stevenson, WA, Oct. 2007).
HOLT, J. E. Logcrypt: Forward security and public verification for secure audit logs. In Australasian Workshops on Grid Computing and E-research (Hobart, Tasmania, Australia, 2006).
HU, L., AND EVANS, D. Secure aggregation for wireless networks. In Symposium on Applications and the Internet Workshops (SAINT) (Orlando, FL, July 2003), p. 384.
ITKIS, G. Cryptographic tamper evidence. In ACM Conference on Computer and Communications Security (CCS '03) (Washington D.C., Oct. 2003), pp. 355–364.
KELSEY, J., CALLAS, J., AND CLEMM, A. Signed Syslog messages. http://tools.ietf.org/id/draft-ietf-syslog-sign-23.txt (work in progress), Sept. 2007.
KILTZ, E., MITYAGIN, A., PANJWANI, S., AND RAGHAVAN, B. Append-only signatures. In International Colloquium on Automata, Languages and Programming (Lisboa, Portugal, July 2005).
KOCHER, P. C. On certificate revocation and validation. In International Conference on Financial Cryptography (FC '98) (Anguilla, British West Indies, Feb. 1998), pp. 172–177.
KOTLA, R., ALVISI, L., DAHLIN, M., CLEMENT, A., AND WONG, E. Zyzzyva: Speculative byzantine fault tolerance. In SOSP '07 (Stevenson, WA, Oct. 2007), pp. 45–58.
LI, J., KROHN, M., MAZIÒERES, D., AND SHASHA, D. Secure untrusted data repository (SUNDR). In Operating Systems Design & Implementation (OSDI) (San Francisco, CA, Dec. 2004).
LIPMAA, H. On optimal hash tree traversal for interval time-stamping. In Proceedings of the 5th International Conference on Information Security (ISC02) (Seoul, Korea, Nov. 2002), pp. 357–371.
LONVICK, C. The BSD Syslog protocol. RFC 3164, Aug. 2001. http://www.ietf.org/rfc/rfc3164.txt.
MA, D. Practical forward secure sequential aggregate signatures. In Proceedings of the 2008 ACM symposium on Information, computer and communications security (ASIACCS'08) (Tokyo, Japan, Mar. 2008), pp. 341–352.
MA, D., AND TSUDIK, G. Forward-secure sequential aggregate authentication. In Proceedings of the 2007 IEEE Symposium on Security and Privacy (Oakland, CA, May 2007), IEEE Computer Society, pp. 86–91.
MA, D., AND TSUDIK, G. A new approach to secure logging. Transactions on Storage 5, 1 (2009), 1–21.
MANIATIS, P., AND BAKER, M. Enabling the archival storage of signed documents. In FAST '02: Proceedings of the 1st USENIX Conference on File and Storage Technologies (Monterey, CA, 2002).
MANIATIS, P., AND BAKER, M. Secure history preservation through timeline entanglement. In USENIX Security Symposium (San Francisco, CA, Aug. 2002).
MANIATIS, P., ROUSSOPOULOS, M., GIULI, T. J., ROSENTHAL, D. S. H., AND BAKER, M. The LOCKSS peer-to-peer digital preservation system. ACM Transactions on Computer Systems 23, 1 (2005), 2–50.
MANULIS, M., AND SCHWENK, J. Provably secure framework for information aggregation in sensor networks. In Computational Science and Its Applications (ICCSA) (Kuala Lumpur, Malaysia, Aug. 2007), pp. 603–621.
MERKLE, R. C. A digital signature based on a conventional encryption function. In CRYPTO '88 (1988), pp. 369–378.
MITRA, S., HSU, W. W., AND WINSLETT, M. Trustworthy keyword search for regulatory-compliant records retention. In International Conference on Very Large Databases (VLDB) (Seoul, Korea, Sept. 2006), pp. 1001–1012.
MONTEIRO, S. D. S., AND ERBACHER, R. F. Exemplifying attack identification and analysis in a novel forensically viable Syslog model. In Workshop on Systematic Approaches to Digital Forensic Engineering (Oakland, CA, May 2008), pp. 57–68.
NAOR, M., AND NISSIM, K. Certificate revocation and certificate update. In USENIX Security Symposium (San Antonio, TX, Jan. 1998).
OSTROVSKY, R., SAHAI, A., AND WATERS, B. Attribute-based encryption with non-monotonic access structures. In ACM Conference on Computer and Communications Security (CCS '07) (Alexandria, VA, Oct. 2007), pp. 195–203.
PAVLOU, K., AND SNODGRASS, R. T. Forensic analysis of database tampering. In ACM SIGMOD International Conference on Management of Data (Chicago, IL, June 2006), pp. 109–120.
PETERSON, Z. N. J., BURNS, R., ATENIESE, G., AND BONO, S. Design and implementation of verifiable audit trails for a versioning file system. In USENIX Conference on File and Storage Technologies (San Jose, CA, Feb. 2007).
PUGH, W. Skip lists: A probabilistic alternative to balanced trees. In Workshop on Algorithms and Data Structures (1989), pp. 437–449.
SAHAI, A., AND WATERS, B. Fuzzy identity based encryption. In Workshop on the Theory and Application of Cryptographic Techniques on Advances in Cryptology (EuroCrypt '05) (May 2005), vol. 3494, pp. 457–473.
SANDLER, D., AND WALLACH, D. S. Casting votes in the Auditorium. In USENIX/ACCURATE Electronic Voting Technology Workshop (EVT'07) (Boston, MA, Aug. 2007).
SCHNEIER, B., AND KELSEY, J. Automatic event-stream notarization using digital signatures. In Security Protocols Workshop (Cambridge, UK, Apr. 1996), pp. 155–169.
SCHNEIER, B., AND KELSEY, J. Secure audit logs to support computer forensics. ACM Transactions on Information and System Security 1, 3 (1999).
SION, R. Strong WORM. In International Conference on Distributed Computing Systems (Beijing, China, May 2008), pp. 69–76.
SNODGRASS, R. T., YAO, S. S., AND COLLBERG, C. Tamper detection in audit logs. In Conference on Very Large Data Bases (VLDB) (Toronto, Canada, Aug. 2004), pp. 504–515.
SONG, D. X., WAGNER, D., AND PERRIG, A. Practical techniques for searches on encrypted data. In IEEE Symposium on Security and Privacy (Berkeley, CA, May 2000), pp. 44–55.
WATERS, B. R., BALFANZ, D., DURFEE, G., AND SMETTERS, D. K. Building an encrypted and searchable audit log. In Network and Distributed System Security Symposium (NDSS) (San Diego, CA, Feb. 2004).
WEATHERSPOON, H., WELLS, C., AND KUBIATOWICZ, J. Naming and integrity: Self-verifying data in peer-to-peer systems. In Future Directions in Distributed Computing (2003), vol. 2584 of Lecture Notes in Computer Science, pp. 142–147.
YUMEREFENDI, A. R., AND CHASE, J. S. Strong accountability for network storage. ACM Transactions on Storage 3, 3 (2007).
ZHU, Q., AND HSU, W. W. Fossilized index: The linchpin of trustworthy non-alterable electronic records. In ACM SIGMOD International Conference on Management of Data (Baltimore, MD, June 2005), pp. 395–406.

翻訳抄

Merkle ツリーを使用した効率的な改ざん証跡ログシステムおよび Merkle 集約に関する 2009 年の論文。Certificate Transparency の基盤であり、一部のブロックチェーンの基盤技術とされている。

Crosby, Scott A., and Dan S. Wallach. Efficient Data Structures for Tamper-Evident Logging. USENIX security symposium. 2009.

	ハッシュチェーン	スキップリスト	履歴ツリー
\({\rm Add}\) 時間	\(O(1)\)	\(O(1)\)	\(O(\log_2 n)\)
\(C_k\) の \({\rm Incr.Gen}\) 証明サイズ	\(O(n-k)\)	\(O(n)\)	\(O(\log_2 n)\)
\(X_k\) に対する \({\rm Membership.Gen}\) 証明サイズ	\(O(n-k)\)	\(O(n)\)	\(O(\log_2 n)\)
キャッシュサイズ	-	\(O(\log_2 n)\)	\(O(\log_2 n)\)
\({\rm Incr.Gen}\) 部分証明サイズ	-	\(O(n-j)\)	\(O(\log_2(n-j))\)
\({\rm Membership.Gen}\) 部分証明サイズ	-	\(O(\log_2 (n-j))\)	\(O(\log_2 (n-j))\)