Merkle Tree
1.  概要
概要
マークルツリー (Merkle Tree) [1, 2] またはハッシュツリー (Hash Tree) は、半順序性を持つデータセットの各要素をハッシュ化し、それらを二分木構造で組み合わせて構築されるデータ構造である。木の各葉ノードは個々のデータのハッシュ値を格納し、各内部ノードは子ノードのハッシュ値を連結してハッシュ化した値を格納する。最上位のルートハッシュはデータセット全体の暗号論的要約として機能し、データの整合性検証に用いられる。
マークルツリーは、主に大量のデータの効率的な検証を目的として 1979 年に Ralph C. Merkle によって発明された。この構造により、データセット全体を保持することなく、特定のデータが更新、破損、改ざんされていないことを対数時間で検証することが可能になる。
マークルツリーは分散ストレージシステム、P2P ファイル共有ネットワーク、ブロックチェーン、データベースシステムなど、データの整合性保証が重要な多くの分野で利用されている。特に、信頼性の低いネットワークやノードが存在する分散環境において、効率的なデータ検証手段として広く利用されている。
Table of Contents
2.  マークルツリーの構築
マークルツリーの構築
基本的なマークルツリーは完全二分木として構成される。葉ノードにはデータのハッシュ値が格納され、各内部ノードには 2 つの子ノードのハッシュ値を連結した値のハッシュが格納される。ツリーの構築は以下の手順で行われる:
各データ \(D_i\) に対してあるハッシュ関数 \(h\) を使ってハッシュ値 \(h_i = h(D_i)\) を算出し、葉ノードを生成する。
隣接する 2 つの葉ノードのハッシュ値を連結してハッシュ値 \(h_{i,i+1}=h(h_i\,||\,h_{i+1})\) を算出し、親ノードを生成する。
ルートノードに達するまで同じ操作を上位レベルに向かって再帰的に繰り返す。
Figure 1 は 8 個のデータ ("To", "be", "or", "not", "to", "be", "that", "is") からマークルツリーを構築する例を示している (実際に SHA-256 を使用して算出している)。各データをハッシュ化して 8 個の葉ノードを生成し、隣接するハッシュ値を連結してさらにハッシュ化することで上位ノードを作成する。
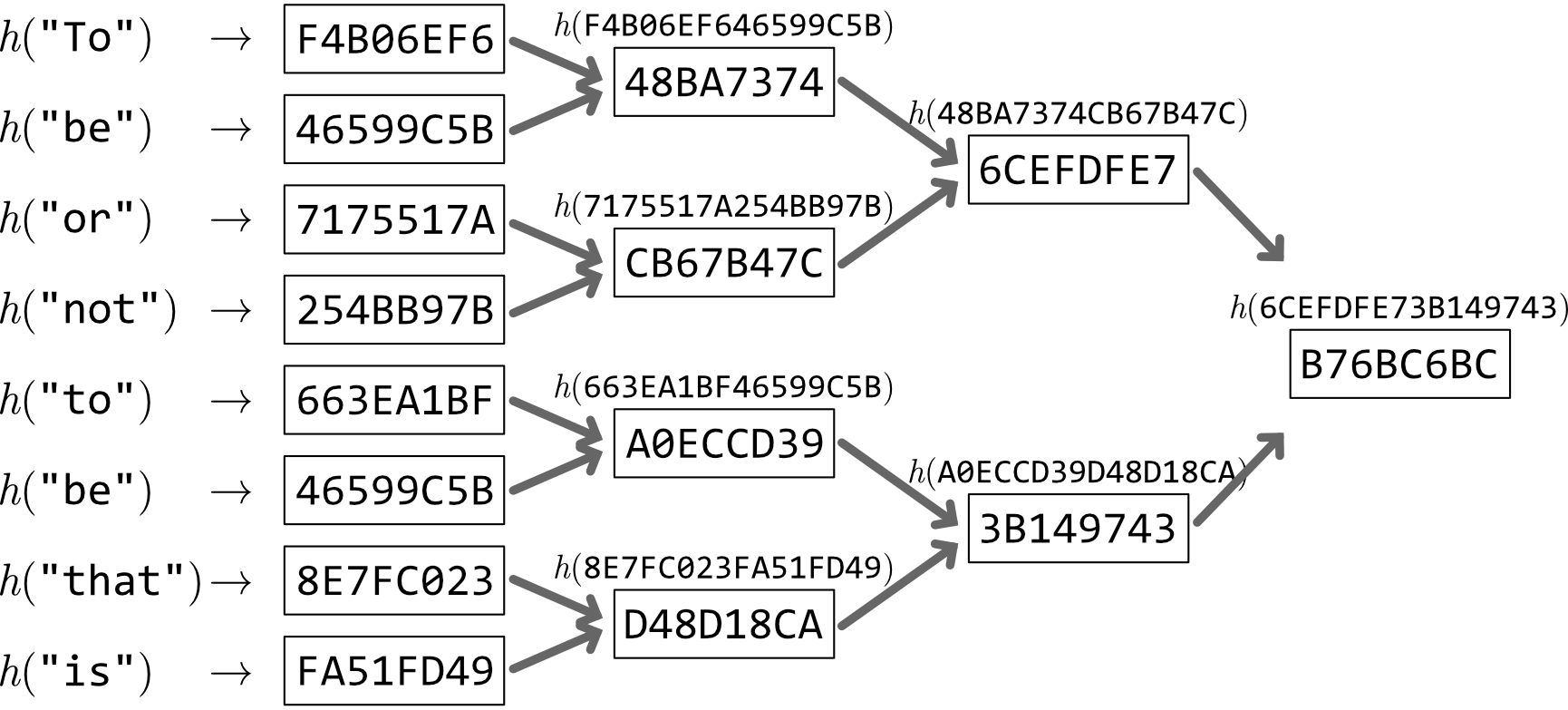
この例では 8 個のデータから高さ 4 のマークルツリーが構築され、単一のルートハッシュ値 B76BC6BC によってデータセット全体が表現される。
データ数が 2 のべき乗でない場合、二分木を構築するために追加の処理が必要となる。一般的な実装では以下のいずれかの方法が採用される:
- 最終ブロックの複製
-
最も単純な手法として、2 のべき乗個となるまで最後のノードを複製する方法がある。例えば \(D_0\) から \(D_4\) の 5 つのデータブロックの場合、6 から 8 番目の葉ノードは \(h_4=h(D_4)\) を複製してツリーを作成する。この方法は実装が簡単だが、同一データの重複により若干の空間的非効率性が生じる。
- 単独ノードの上位昇格
-
より効率的な方法として、同じレベルでペアを持たないノードをそのまま上位レベルに昇格させる方法がある。5 つのデータブロックの例では \(h(D_4)\) を第 1 レベルに直接昇格させ、最終的にルートハッシュは \(h(h(h(h_0 || h_1) || h(h_2 || h_3)) || h_4)\) のような非対称な構造で算出される。この方法はストレージ効率に優れるが、実装がやや複雑になる。
- パディングによる補完
-
データセット末尾に空のブロックやダミーデータを追加し、2 のべき乗個まで補完する方法がある。この場合、パディングされたブロックには既定の値 (通常は 0) を使用し、\(h(0)\) などの固定値で葉ノードを生成する。
- 空の中間ノードの追加
-
History Tree [3] では完全二分木をベースの形として、データが存在しない部分木のルートノードを \(h(\emptyset)\) などの空のハッシュ値と置き換えることで部分木全体の保存空間を節約する。
BitTorrent プロトコルでは最終ブロックの複製方式、Bitcoin 等の多くのブロックチェーンシステムでは単独ノードの昇格方式を採用している。どの方式を選択するのが最良かは、実装の複雑さ、ストレージ効率、および既存システムとの互換性要件に依存する。
3.  データの検証
データの検証
ハッシュ関数における雪崩効果 (avalanche effect) は、元データに 1 ビットでも変更があるとハッシュ値が完全に異なる値になることである。この性質により、マークルツリーでは 2 つのデータセットが同一であるかをそれぞれのルートハッシュを比較するだけで判断できる。さらに、ハッシュ値がツリー構造を構成していることにより、差異のあるハッシュ値の枝を葉に向かって下ることで、差異のあるデータを効率的に見つけることができる。
Figure 2 は Figure 1 における "be" を "pee" に変更した例である。変更のあった "pee" の葉ノードからルートノードまでのハッシュ値が全く違う値になることが分かる。
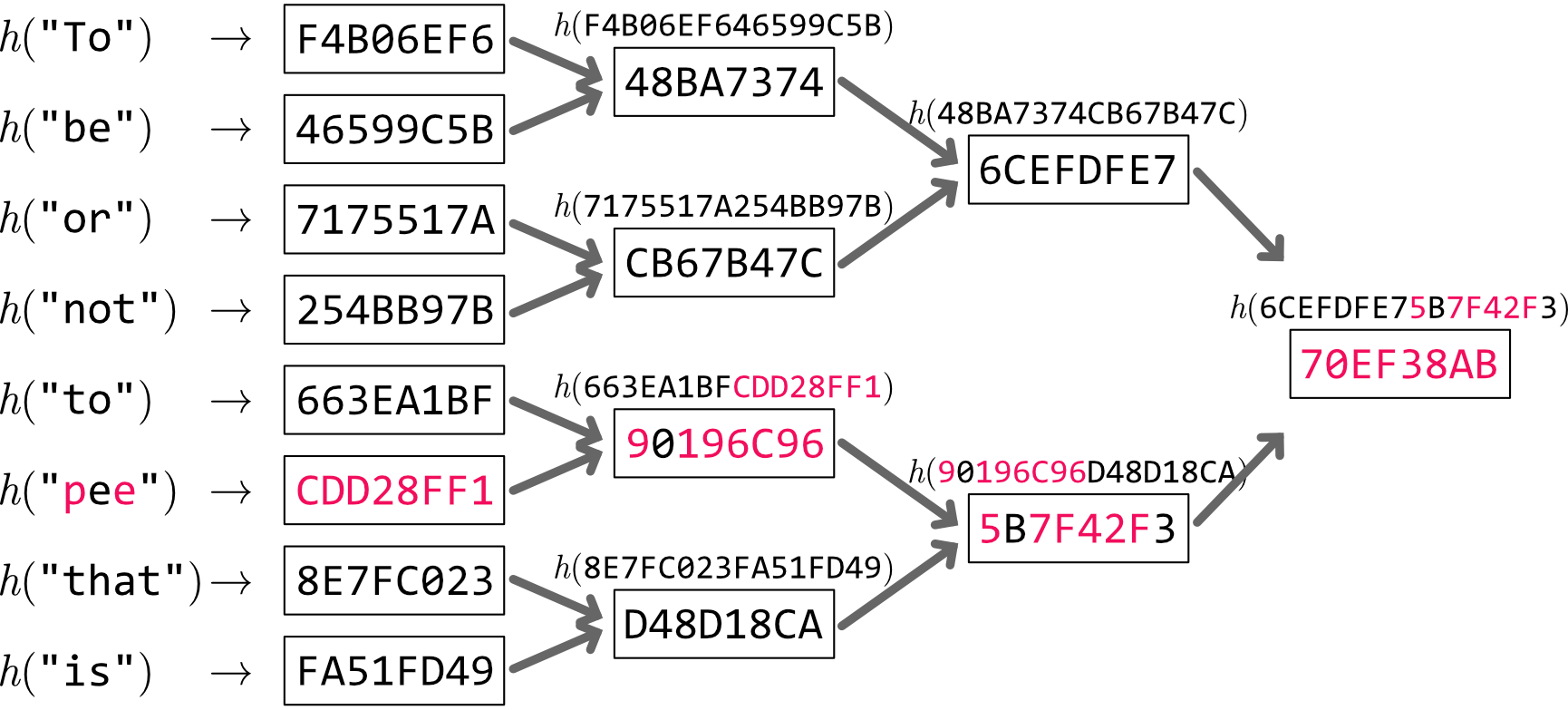
3.1.  異なるデータの特定
異なるデータの特定
データセット A と B のルートハッシュが一致する場合、暗号論的ハッシュ関数の衝突耐性により A と B は同一のデータセットであると見なすことができる。逆に、ルートハッシュが異なる場合、少なくとも 1 つのデータに差異が存在すると判断できる。
マークルツリーはハッシュ値をツリー状に配置した構造を持つため、2 つのマークルツリーから差異のあるデータを効率的に特定できる。ルートノードから開始し、ツリーの各レベルで対応するノードのハッシュ値を比較して異なるハッシュを持つ子ノードを絞り込んでいくことで、変更されたデータまで対数時間で辿り着くことができる。具体的な手順は次の通りである:
ルートノードで差異を検出する。
2 つの子ノードのハッシュ値を比較し、ハッシュ値の異なる部分ツリーを選択する (両方の子ノードが異なっている可能性があることに注意)。
葉ノードに到達するまで同様の比較を繰り返す。
最終的に特定された葉ノードが、差異のあるデータである。
この探索過程では各レベルで候補が半分に絞り込まれるため、\(n\) 個のデータを持つツリーにおいて差異のある 1 つのブロックを \(O(\log n)\) 回の比較で特定できる。例えば 1,000,000 個のデータブロックを持つデータセットでも最大 20 回程度の比較で変更箇所を特定可能である。
差異のあるデータ数が \(m \le n\) 個存在する場合、各レベルで差異を持つノードの数が増加するため、探索すべき部分木が増大する。最悪のケースはすべてのデータが異なる \(m = n\) のケースで、これはツリー上のすべてのノードで差異が発生するため、2 つのツリーのすべてのノードを完全に走査する必要がある。したがって、完全二分木のノード数 \(2n-1\) より、最悪計算量は \(O(n)\) となる。
分散システムでは、差分レプリケーション (差分バックアップ) やアンチエントロピー機構において、差異のあるデータを特定する目的でマークルツリーが使用されている。
3.2.  部分データの検証
部分データの検証
マークルツリーの主要な利点の一つは、データセット全体を保持することなく特定のデータの整合性を検証できることである。言い換えると、メンバーシップ検証 (membership verification) が可能である。検証者は事前に信頼できるルートハッシュのみを保持し、検証対象のデータと包含証明 (inclusion proof) または認証パス(authentication path)と呼ばれる最小限のハッシュ値セットを用いて検証を行う。
3.2.1.  例: データ検証
例: データ検証
部分データ検証の実用例を Figure 3 に示す。この例では、クライアントが信頼できるルートハッシュを事前に保持しており、計算処理のためにデータセットから \(D_5\) のみをサーバに要求する状況である。
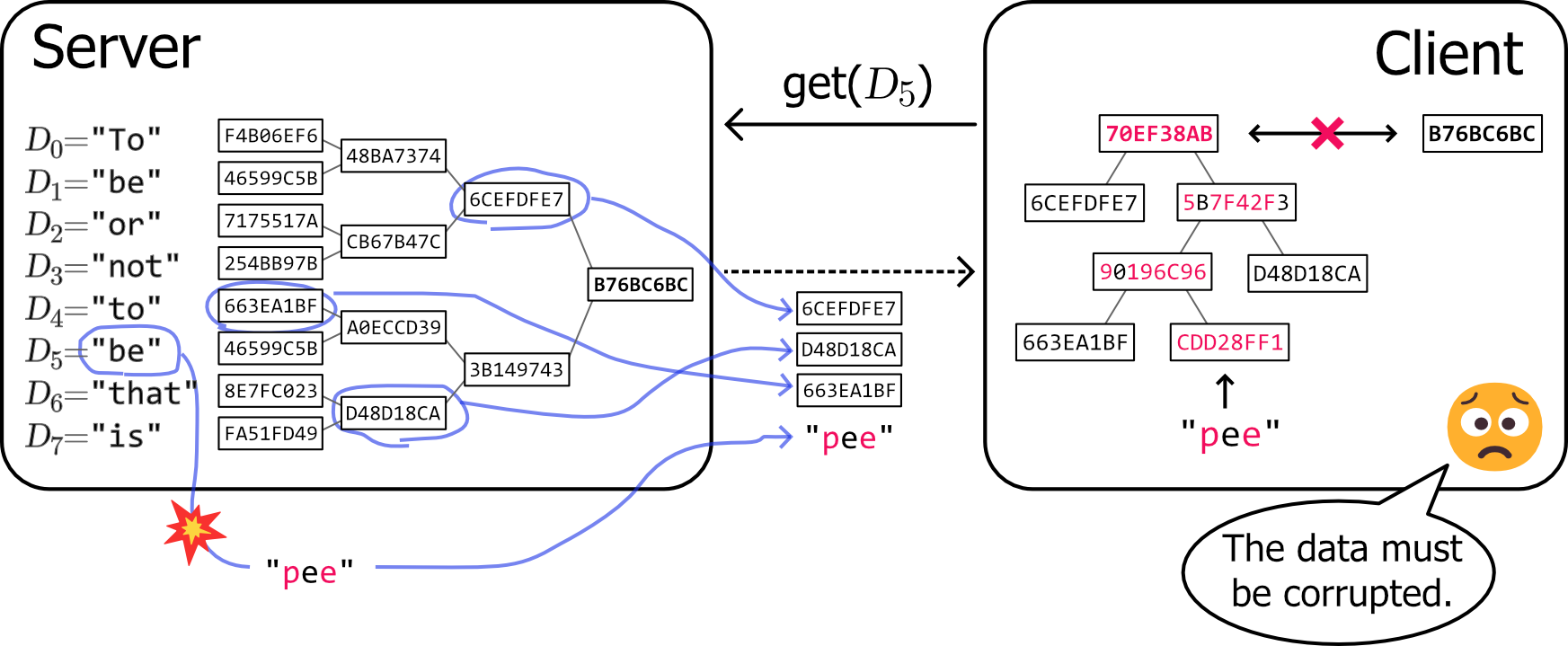
このシナリオでは、クライアントは何かを計算するためにデータ \(D_5\) をサーバに要求する。しかし、何らかの理由でクライアントが取得した \(D_5\) が破損していた。しかし、クライアントはデータと共に取得した包含証明からルートハッシュを計算して、自身の持つ信頼できるルートハッシュと比較することで、このデータ (または包含証明) が破損していることを検出できる。
サーバが悪意をもってデータを改ざんしようとしても、ルートハッシュを一致させるような包含証明を意図的に作成することは困難であることに注意。マークルツリーで使用するハッシュ関数は用途に応じて選択される。悪意のある改ざんからの保護が必要な場合は SHA-256 や SHA-3 などの暗号学的ハッシュ関数が必要である。一方、単純なデータ破損の検出が目的であれば aHash などの高速な非暗号論的ハッシュ関数 (あるいはもっと弱いチェックサム) も考慮することができる。
3.2.2.  例: チケット購入者の確認
例: チケット購入者の確認
あるイベントがあり、チケット発行会社が購入者リストを保持している。ただし、セキュリティの観点から購入者リストをイベント運営会社 (外部の業者) に渡したくない。受付に来た客のチケットが正規のものであることを、イベント運営会社はどう確認すれば良いだろうか?
チケット発行会社は購入者リストを Merkle Tree 化し、チケットには購入者の包含証明を記載して渡す。またイベント会場の受付には購入者リストのマークルルート値をあらかじめ伝えておく。受付は、客の提示したチケットからルートハッシュを算出し、それがチケット発行会社から伝えられたハッシュ値と一致していれば、そのチケットが正規に購入されたものであることを確証できる (本人確認は別途必要)。
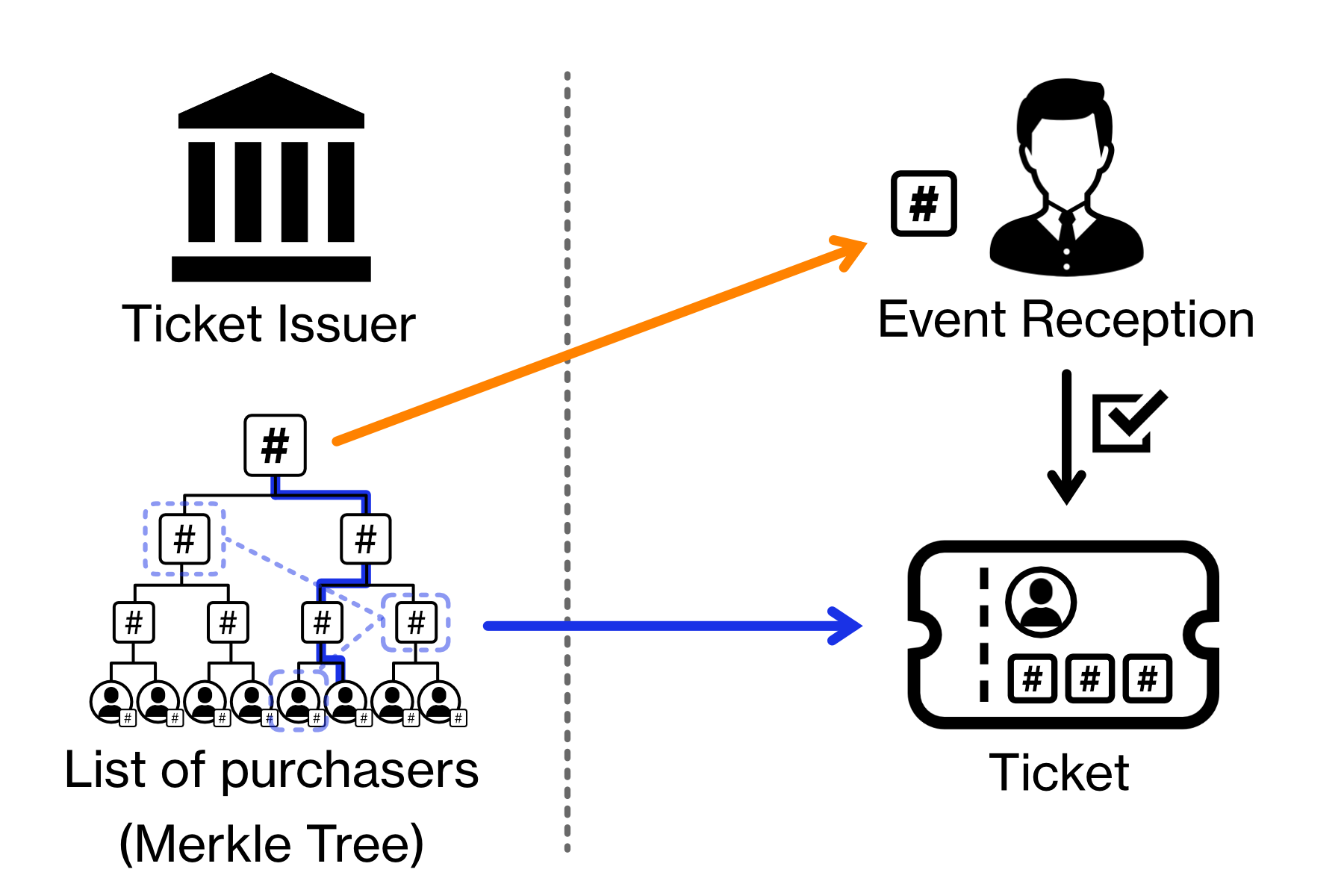
この方法には 2 つの利点がある。一つは、チケット発行会社とイベント運営会社の間で購入者リストを受け渡す必要がないこと。もう一つは、イベント運営会社はイベント当日にチケット発行会社のシステム状況に依存せずにチケット購入の確認ができることである。ただし、実際にはツリーが確定する (チケット販売が終了する) までルートハッシュも包含証明も確定できないため、実際のチケット送付がそれ以降になるというような、現実的な問題をクリアする必要がある。
4.  マークルツリーの変種
マークルツリーの変種
マークルツリーの基本的なアイディアはデータの整合性を検証するために設計されている。しかし、現実適用する上では対象とするアプリケーション要件に合わせてカスタマイズする必要があったり、異なるデータ構造やアルゴリズムと組み合わせて追加の効果を提案するアイディアの余地が多くあるため、様々な変種が提案されている。
4.1.  スパースマークルツリー
スパースマークルツリー
葉の数 \(n\) が非常に大きいが (例えば \(n=2^{256}\))、そのほとんどが 0 や null といった値を持たない (つまりデフォルト値の) マークルツリーをスパースマークルツリー (sparse merkle tree; 疎マークルツリー) と呼ぶ。\(n\) 個の葉のうち \(k\) 個が有効な値の場合、レベル 0 のノードのうち \(n-k\) 個はデフォルト値 \(h_*=H(0)\) を持つことになる。同様にレベル 1 のほとんどは \(h_*=H(H(0)\,|\,H(0))\) である。このようにスパースマークルツリーのほとんどの中間ノードはデフォルト値のままである。このようなスパースマークルツリーのルートハッシュはデフォルト値のハッシュ計算を省略することで \(O(k \log n)\) の計算コストで算出することができる。
疎となることが前提のマークルツリーはデフォルト値となる葉やノードを省略してパトリシアツリー (Patricia tree) またはマークルパトリシアトライ (Merkle Patricia trie) と呼ばれる構造を適用することができる。例えば Ripple や Ethereum ではスパースマークルツリーとしてパトリシアツリーを使用している。
4.2.  Merkle Search Tree
Merkle Search Tree
B-Tree は現実的なデータベースのインデックスなどに使われている効率の良い多分岐検索木であるが、B+Tree や B*Tree といった代表的な変種も含めて決定論的な構造ではない。一方で、検証を目的とする Merkle Tree は、同じデータセットに対して挿入や削除の順序によらず必ず同じ木構造が生成されるという決定論的な性質を持つ必要がある。そのため、B-Tree に似た平衡多分岐検索木でありながら決定論的な木構造を Merkle Tree に適用するいくつかの試みがある。
Merkle Search Tree (MST) [4] はソートされた Key-Value ペアを格納できる Merkle Tree である。これは、各キーをハッシュ化し、\(B\) 進数で表現したときの先頭の 0 の数のレベルにそのキーを配置することで構築される。これにより確率的に平衡なツリー構造となり、B-Tree に似た多分岐検索木でありながら、同一のデータセットに対して常に同じ構造が生成される決定論性を持たせることができる。
MST は効率の良い検索木でありながら、2 つの独立したデータセットの検証、差分検出、修復といった Merkle Tree としての特性も併せ持っている。このような MST は厳密な順序性と決定論性が必要なシステムに適しており、大規模ネットワークや P2P のようなオープンネットワークで因果一貫性を持つ状態ベース CRDT として、Bluesky の AT Protocol で Key-Value ストアのアンチエントロピー機構として使用されている [5]。
Figure 5 は実際に A から Z までの文字で SHA-256 ハッシュを計算し、基数 \(B=3\) で構築した MST の例である (右に偏っているように見えるが木構造の観点では概ねバランスしている点に注意)。\(B\) の値を大きく設定しキーを増やすと 1 ノードあたりのキー数が増え、より平衡木に近い構造になるだろう (なお元の論文 [4] では \(B=16\) を適用している)。
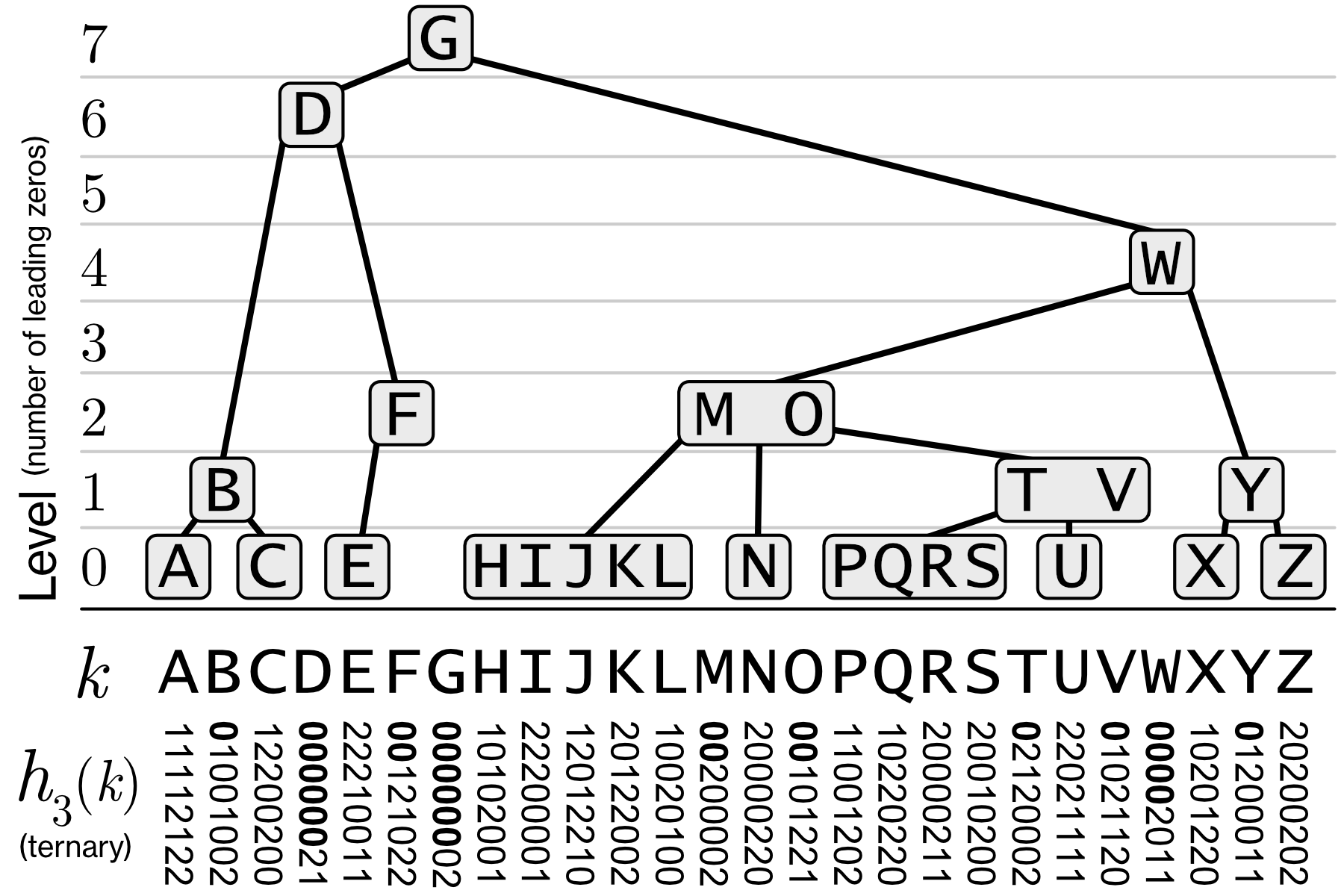
MST におけるツリー構築の核心は、特定の確率的条件を満たすハッシュ値を持つキーをキー範囲の境界として分断することで、確率的に平衡な多分木構造を構築することである。ここで確率的条件とはハッシュ値の先頭に 0 が何個存在するかを意味する。
レベル \(\ell=0\) の葉ノードは、ハッシュ値 \(h_3(k)\) の先頭に 0 を持つキーによって分断されたキー列によって構成される。したがって、1 つの葉ノードに含まれるキー数の期待値は \(B-1\) (基数 \(B\) における digit の中で 0 以外の digit の数) であり、\(\ell=0\) には率にして全体の \(\frac{B-1}{B}\) 程度のキーが配置される。
レベル \(\ell=1\) の中間ノードには、ハッシュ値の先頭に 0 を持つキーが含まれており、00 を持つキーによって分断される。したがって、1 つの中間ノードに含まれるキー数の期待値は \(B-1\) であり、率にして全体の \(\frac{1}{B} \frac{B-1}{B}\) 程度のキーが \(\ell=1\) に配置される。
レベル \(\ell=2\) の中間ノードには、ハッシュ値の先頭に 00 を持つキーが含まれており、000 を持つキーによって分断される。したがって、1 つの中間ノードに含まれるキー数の期待値は \(B-1\) であり、率にして全体の \(\frac{1}{B^2} \frac{B-1}{B}\) 程度のキーが \(\ell=2\) に配置される。
これを一般化すると、MST の各ノードは平均で \(B-1\) 個のキーを含み、中間ノードであれば平均して \(B\) 個の子ノードを持ち、あるキーがレベル \(\ell\) に配置される確率は \(\frac{1}{B^\ell} \frac{B-1}{B}\) となる。
2 つの MST を比較するときは、通常のハッシュツリーのようにルートから順にハッシュ値を比較する。この差分探索の計算量は \(O(\log_B n)\) となる。
4.3.  Prolly Tree
Prolly Tree
Prolly Tree (Probabilistic Merkle Tree) も Merkle Search Tree と非常によく似た仕組みを持ち、キーのハッシュ値の確率的条件に基づいてキー範囲を分断してツリー構造を生成する。MST との違いは、順序付けされたキーの並びに対してローリングハッシュで算出したハッシュ値から境界となるキーを決定するという点である。
与えられたデータ列を特定のアルゴリズムに基づいて小さな塊 (chunk) に分割することを Chunking と呼んでいる。特定のアルゴリズムとは、MST と同様に、例えばキーのハッシュ値の先頭や末尾にいくつのゼロが存在するかといった条件である。
ローリングハッシュは、データ列でウィンドウ (範囲) を移動させながら、そのウィンドウに入っているデータからハッシュ値を算出する手法である。ここで、ウィンドウを 1 つ移動する時に、移動前のハッシュ値から \(O(1)\) で移動後のハッシュ値を算出することができる (ウィンドウサイズに依存せずに) という特徴を持つ。キー列にローリングハッシュを適用する場合、ある位置でのデータ挿入、変更、削除はウィンドウ範囲内のハッシュ値のみに影響する。つまり、ローリングハッシュを使用してチャンク境界を決定するスキームでは、Key-Value の変更に対して局所的なチャンク境界に影響が出るものの、他の大多数のチャンクには影響が及ばず、ツリー全体の構造は大きく変わらないとされている。
Prolly Tree の比較は MST と同様にルートから順にハッシュ値を比較する。Prolly Tree はローリングハッシュによりツリー構造の安定性が良いため、データが頻繁に更新される環境や、ネットワークを介して効率的に同期を行う場合に有用であり、また MST と同様に分散システムでのデータ同期や CRDT の実装に向いている。
Prolly Tree についてネットを検索すると Merkle Search Tree (2019) は Prolly Tree (2015) の再発明であるといった主旨の記事が Dolt のブログで見つかる。Dolt は Prolly Tree 上に構築されたバージョン管理型 SQL データベースである。ただし、Prolly Tree は技術文書のみの記載であり、一方で Merkle Search Tree は査読付き論文として発表されている違いがある。
4.4.  History Tree
History Tree
Merkle ツリーの亜種である History Tree [3] は追加が可能な改ざん証跡ログシステムを提案している。通常の Merkle Tree が静的なデータセットの完全性を保証するのに対し、History Tree は動的に成長するログの一貫性を効率的に検証できる。また、ある時点 \(m\) のルートが、より後の時点の \(n \gt m\) の木構造に含まれていること、つまり、バージョン指定で過去のスナップショットを自然に保持している。
History Tree は、特定のログがあるスナップショットの葉ノードとして存在していることを示す包含証明に加えて、2 つのスナップショット間で後者が前者の純粋な拡張であることを示す一貫性証明を提供する。いずれも証明サイズと検証計算量はデータ数 \(n\) に対して \(O(\log n)\) である。
History Tree は公開 CA の証明書発行を追跡し誤発行を検出することを目的とした Certificate Transparency (CT) のログ構造として応用されている。Google の Trillian は CT の設計を一般化した Transparency Log 基盤であり、Let's Encrypt などの運用実例も公開されている。
またこの研究では、中間ノードに属性を持たせることで、データセットの簡易的な検索を行うことができる Merkle 集約 (Merkle aggregation) も提案している。このアイディアでは中間ノードに Bloom Filter を設置することができる。
5.  参考文献
参考文献
- Merkle, R.C. (1979). A Certified Digital Signature. In: Brassard, G. (eds) Advances in Cryptology — CRYPTO’ 89 Proceedings. CRYPTO 1989. Lecture Notes in Computer Science, vol 435. Springer, New York, NY. https://doi.org/10.1007/0-387-34805-0_21
- Merkle, R.C. (1987) A Digital Signature Based on a Conventional Encryption Function. Conference on the Theory and Application of Cryptographic Techniques, Santa Barbara, 16-20 August 1987, 369-378. https://doi.org/10.1007/3-540-48184-2_32
- Crosby, Scott A., and Dan S. Wallach. Efficient Data Structures for Tamper-Evident Logging. USENIX security symposium. 2009.
- Alex Auvolat, François Taïani. Merkle Search Trees: Efficient State-Based CRDTs in Open Networks. SRDS 2019 - 38th IEEE International Symposium on Reliable Distributed Systems, Oct 2019, Lyon, France. pp.1-10, ff10.1109/SRDS.2019.00032ff. ffhal-02303490f
- KLEPPMANN, Martin, et al. Bluesky and the at protocol: Usable decentralized social media. In: Proceedings of the ACM Conext-2024 Workshop on the Decentralization of the Internet. 2024. p. 1-7.
論文翻訳: A CERTIFIED DIGITAL SIGNATURE
公開鍵暗号に依存せず、従来の暗号化関数のみを使用して一方向関数とツリー構造を組み合わせたデジタル署名システムを提案する 1979 年の論文。現代の Merkle Tree やハッシュベース署名の基礎となる先駆的研究である。…
論文翻訳: A DIGITAL SIGNATURE BASED ON A CONVENTIONAL ENCRYPTION FUNCTION
従来型暗号化関数のみに基づき、素因数分解の困難性やモジュラー算術の高い計算コストに依存しないデジタル署名システムについて論じた 1987 年の論文。R.C.Merkle が以前に提唱したツリー構造に基づく認証 (後の Merkle Tree の基礎) を、従来型暗号化関数を用いたデジタル署名システムへ応用し、その実用性を高めている。…
論文翻訳: Efficient Data Structures for Tamper-Evident Logging
Merkle ツリーを使用した効率的な改ざん証跡ログシステムおよび Merkle 集約に関する 2009 年の論文。Certificate Transparency の基盤であり、一部のブロックチェーンの基盤技術とされている。…
論文翻訳: Merkle Search Trees: Efficient State-Based CRDTs in Open Networks
キーの順序を維持しながら決定論的に平衡 (バランス) を維持するマークル検索木 (MST) を提案する 2019 年の論文。従来の CRDT 実装はベクタークロックのような因果ブロードキャストに依存しているため大規模ネットワークやオープンネットワークで効率的に実装するのは難しいが、MST によりそのようなネットワーク上で状態ベース CRDT を効率的に実装できる。…

